基于运动特性的农机导航控制方法
2021-12-07白晓平
白晓平 孟 鹏 王 卓 时 佳
(1.中国科学院沈阳自动化研究所, 沈阳 110016;2.辽宁省农业装备智能化技术重点实验室, 沈阳 110016; 3.中国科学院大学, 北京 100049)
0 引言
随着“智慧农业”的提出,农业机械(农机)自动导航技术已经成为了智能化精准农业中的重要组成部分[1-8]。为了提高农机导航控制的精度和稳定性,许多学者对农机运动学模型和导航控制方法进行了大量的研究[9-21]。运动学模型的研究仍旧主要集中在KELLY[22]提出的传统“二轮车模型”方面;控制方法的研究则不再局限于传统的输出控制上,路径跟踪模型控制也成了一个重要的研究方向。由于农机作业环境较差,轮胎与地面作用过程复杂,建立精确的动力学模型比较困难,现有模型多采用传统“二轮车模型”和传统输出控制方法进行导航控制器设计。传统“二轮车模型”的优点是运动学模型简单,考虑因素较少,易于建模;缺点是模型精度较低,会给基于模型的控制方法的控制效果带来不良影响,这会成为进一步提高农机自动导航精度的最大阻碍。
国内外众多学者对路径跟踪控制方法的研究,包括基于农机运动学模型的控制算法和基于农机动力学模型的控制算法[23-25]。农机运动学模型采用小角度近似化方法简化两轮车运动学模型,主要考虑了农机的运动学约束对农机控制的影响,建模简单,便于设计控制器实现对农机转向的有效控制。但是多处采用小角度近似替代,在曲线跟踪过程中控制系统会存在稳定性变差问题,这种建模方法适用于低速行驶农机或对横向误差要求不是很高的农机。农机动力学模型主要通过车轮与地面之间的复杂作用来对车辆进行建模,在一定环境中可以满足农机路径跟踪时的稳定性控制要求。但是忽略了农机作业环境的复杂性和不确定性,建立动力学模型较为困难。同时,农机作业环境发生改变,基于农机动力学模型设计的控制器也会发生较大偏差,不适用于多种作业环境下的农机建模。
精确的农机运动学模型可以提高路径跟踪控制器的控制品质,减小农机在路径跟踪过程中的误差。传统二轮车运动学模型通常利用后轮为目标点进行运动学分析,采用小角度近似将三角函数转换为线性函数和小角度近似替代而简化运算,只考虑横向偏差和航向偏差,忽略了车辆侧偏角对车辆航向的影响。本文将以车辆质心为目标点进行运动学建模分析,在建立的车辆运动学模型中引入侧偏角,以提高方向角精度和控制器的收敛速度,减小小角度近似替代带来的误差,并基于该模型进行状态反馈控制器设计。
1 农机运动学模型
1.1 侧向运动分析
图1所示二轮车模型中,左右2个前轮由位于点A的车轮代替,后轮由位于点B的中央后轮代替。前轮转向角用δ表示。此模型成立的前提是假设前轮转向,后轮驱动且后轮不可转向。图中坐标系XOY为大地坐标系,点C为车辆的瞬时旋转中心,车辆质心为点D,从农机质心到点A和点B的距离分别为lf和lr,农机轴距为l=lf+lr,R为农机旋转半径,v为农机质心处速度,ψ为农机当前时刻的航向角,β为农机侧偏角即车辆质心处速度方向与前后轮轴向之间的夹角,利用三角形内角与外角之间的关系,由△CO′A与△CO′B可得三角形各内角值。
当时间t=t1时,在△CDA和△CDB上分别使用正弦定理得
(1)
(2)
(3)
由式(3)得
(4)
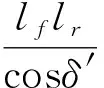
(5)
将式(2)两侧同时乘以lflr可得
(6)
可由式(5)减去式(6)得到侧偏角β为
(7)
1.2 运动学建模
在不考虑车轮与地面的相互作用,无侧倾、俯仰、侧滑等运动的情况下,可将拖拉机、插秧机等多种四轮农机简化为二轮车模型进行运动学分析。在建模过程中将侧偏角引入农机运动学模型,提高农机方向角的精度。定义速度方向与车辆纵轴方向为侧偏角β。农机运动学模型示意图如图2所示。
图2中,S为理论路径,点E和点G分别对应t1和t2时刻车辆在理论路径S上的位置,EK和KG分别对应点E和点G的切线,β-θ为航向偏差角,γ为航向角变化量,y为车辆当前位置的横向偏差,dy为dt=t2-t1时间内横向偏差的变化量,dθ1为实际航向角变化量,由图中几何关系可知dθ=γ,dθ2为理论航向角变化量。
当dt非常小时,由△BB′H得
dy=vcosβsinθdt
(8)
如图2所示△CEF~△CHB′,且
(9)
式中lCE——理论路径瞬时旋转半径
lCH——理论路径瞬时旋转中心到后轮的距离与车辆横向位移之和
lB′H——实际路径中车辆在相邻时刻dt内后轮移动的距离
lEF——理论路径中车辆在相邻时刻dt内后轮移动的距离
由式(9)可得
(10)
假设曲率c(x)和速度v均为一固定范围内的值,当dt很小时,sinθ趋向于0,dt趋向于0,可将c(x)vcosβsinθdt近似为0,所以可将式(10)近似化为
(11)
航向角变化量由2部分组成:dθ=dθ1+dθ2,由图2所示几何关系可知
(12)
将式(12)代入dθ可得
(13)
综合式(8)、(11)、(13),可得农机运动学模型为
(14)
实际情况中,曲率c(x)和横向误差y一般小于1,所以1-c(x)y≠0,在模型推导过程中采用小尺寸近似替代和极小项近似为0的方法,所以实际情况下,曲率c(x)越小,模型的精度越高,控制效果也更好。
2 控制器设计

其中
根据线性系统理论,对该系统采用极点配置法可以获得渐近稳定的控制率。由rank(BAB)=2可知,系统完全可控,可对其进行极点配置。在s平面上选择一组合理的、具有所期望性能品质指标的极点-3±2j为该闭环系统的极点。反馈控制率为
u=-KX
(15)
其中
K=[k1k2]
(16)
(17)
将式(14)、(17)代入式(15)得

(18)
由式(18)可得
(19)
参数k1和k2的影响因素主要有3方面:极点配置得到的比值、车辆转向机构的性能和农机作业环境。在确定参数k1和k2的比值后,根据农机作业时的实际工作环境对具体取值进行适当调整。
3 实车实验
3.1 实验平台
实验平台为配有自动导航控制系统的拖拉机,前轮转向,后轮驱动,如图3所示。
实验平台上的自动导航控制系统采用分布式控制策略,由位置检测单元、航向检测单元、导航控制器和转向控制单元4部分组成,各部分之间通过CAN总线进行通信。其中,位置检测单元由GPS和智能节点组成,GPS实时采集车辆的位置信息,采样频率为20 Hz,定位精度为(0.01±10-12)m。航向检测单元由惯导MTI和智能节点组成,MTI实时采集车辆的航向信息,采样频率为20 Hz,测量精度为±1°。
3.2 实验设计
车辆行驶速度v=1.0 m/s。模型控制参数根据极点配置法得到的比例值结合实际情况微调。采用高精度GPS采点并获取车辆当前位置信息,惯导MTI获取车辆航向信息,车辆控制器从CAN总线上获取位置信息和航向信息进行解析。
实验过程:在实验场地选取A、B两点,将A、B两点确定的直线作为车辆跟踪的目标路径,如图4所示,在点A附近启动车辆和控制程序开始预定路径的跟踪,并从CAN总线实时获取车辆当前位置信息和航向信息,当车辆接近点B时,停止数据采集;曲线路径跟踪实验的目标路径是由2条直线和2条曲线组合而成,需在实验场地采集6个点,目标路径如图5所示,实验过程和数据采集过程与直线路径跟踪实验类似。
设计2组对照实验:第1组为基于传统二轮车运动学模型设计的控制方法进行路径跟踪;第2组为基于优化后的运动学模型设计的控制方法进行路径跟踪。车辆从起始点出发时开始从CAN总线上采集数据,接近终点时停止数据采集,对设定路径段内的2组对照实验数据分别进行路径跟踪分析和误差分析,并将2组实验进行对比分析。
3.3 实验结果及分析
采用不同的运动学模型,相同的控制方法(以状态反馈控制方法为例)设计对照实验证明本文提出优化模型的有效性。
3.3.1直线路径跟踪
第1组实验的直线路径跟踪局部放大情况如图6a所示;第2组实验的直线路径跟踪局部放大情况如图6b所示。
2组实验的直线跟踪误差分别如图7所示。
2组对照实验的直线路径跟踪实验统计结果如表1所示。
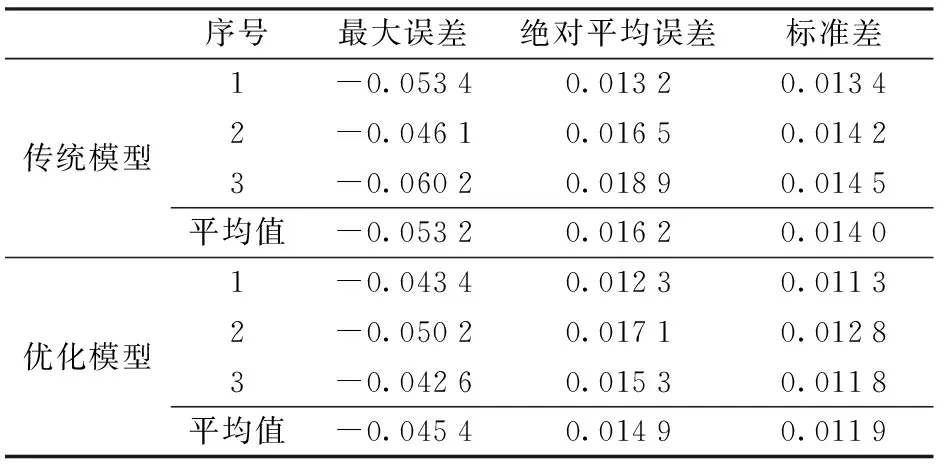
表1 控制直线路径跟踪横向误差统计Tab.1 Control statistics of lateral error in linear path tracking m
由图7和表1可知,基于优化后运动学模型设计的控制方法在直线路径跟踪时与基于传统二轮车模型设计的路径跟踪控制方法相比,最大横向误差、绝对平均误差以及标准差均有所减小。表明在直线路径跟踪过程中,控制方法中加入侧偏角可以在一定程度上提高控制方法的精度和稳定性。
直线行驶状态下,当航向偏差角和横向偏差较小时,侧偏角近似为0,对控制器的影响很小;当航向偏差或横向偏差较大时,侧偏角增大,可提高控制器的收敛速度,对控制器有一定的影响。
3.3.2曲线路径跟踪
第1组实验未考虑农机侧偏角,曲线路径跟踪局部放大情况如图8a所示;第2组实验在运动学模型建模过程中引入侧偏角β,曲线路径跟踪局部放大情况如图8b所示。
2组实验的曲线跟踪误差如图9所示。对曲线路径的跟踪实验统计结果如表2所示。
由图9和表2可知,优化模型控制的曲线路径跟踪横向误差与传统模型控制相比,绝对平均误差减少0.022 9 m,标准差减少0.033 6 m,两者均有大幅降低。表明在农机运动学模型建模过程中加入侧偏角对路径跟踪控制方法的控制精度有很大提高,会提高控制方法的控制性能。
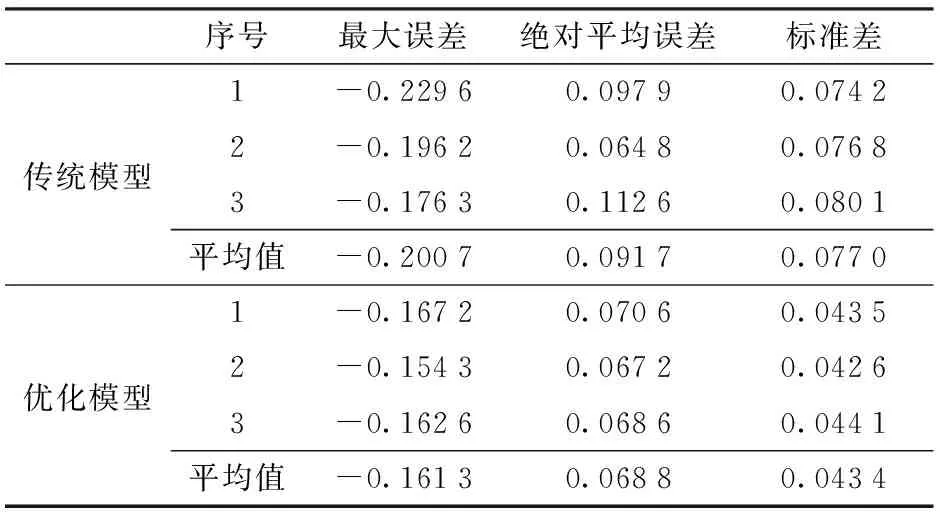
表2 控制曲线路径跟踪横向误差统计Tab.2 Control curve path tracking lateral error statistics m
曲线行驶状态下,传统二轮车运动学模型只考虑了航向偏差和横向偏差,采用了小角度近似替代;优化后的模型将侧偏角引入运动学模型,提高车辆建模精度,曲线行驶过程中侧偏角对车辆航向角的影响较大,可有效提高控制器的收敛速度。
4 结束语
针对农机运动学模型中的传统二轮车模型只考虑横向误差和航向误差而采用小角度近似替代的问题,本文提出了一种考虑车辆侧偏角的农机运动学建模方法,在传统运动学模型的基础上加入侧偏角β弱化小角度近似替代带来的误差,有效提高农机运动学模型的建模精度。通过实车道路实验测试结果表明,2组对照实验曲线路径跟踪的绝对平均横向误差分别为0.091 7、0.068 8 m,标准差分别为0.077 0、0.043 4 m,实验结果表明本文提出的农机运动学建模方法对路径跟踪控制方法在曲线路径跟踪时的控制性能有明显提升。
