回收锥与回收函数的若干性质

史小波，徐茂杨

（重庆师范大学 数学科学学院，重庆 401331）

回收锥和回收函数作为凸分析中的重要研究对象，在最优化理论中有广泛的应用。其中，回收锥可以用来刻画集合的有界性，而回收函数作为一种特殊的上凸近似，可以刻画最优化问题解集非空性等。文献［1-2］给出了凸集和凸函数回收锥、回收函数的概念，并给出了简单的基本性质及其应用。1990 年，黄学祥［3］针对非凸集合和非凸函数给出了广义回收锥和广义回收函数，推广了已有的性质。近年来，一些学者进一步研究回收锥和回收函数的等价刻画及其性质，并将结果应用到最优化问题中，刻画了最优解集的非空性。本文以文献［1-2］中回收锥和回收函数的性质作为理论基础，在文献［4-5］回收锥和回收函数的相关性质下，针对回收锥和回收函数作了进一步的研究。

1 预备知识

设Rn为n 维欧几里得空间，d∈Rn，C⊆Rn，若对于任意的x∈C，d≥0，有

则称d 为C 的一个回收方向。所有回收方向的全体称为C 的回收锥，记为Rc，即

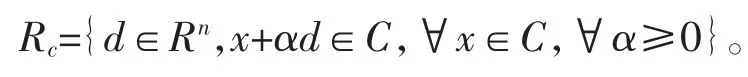
设f：Rn→R∪｛+∞｝，且dom f=Ø，epi f=｛（x，α）∈Rn×R，f（x）≤α｝为凸集。若（y，v）∈O+（epi f），则由回收锥定义有

即

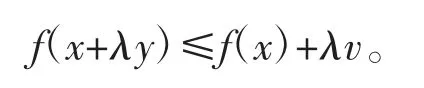
若存在一个函数g 满足

称g 为f 的回收函数，记作rf。

由定义，文献［1］又给出了回收函数如下的等价定义，即

为了研究回收锥和回收函数的性质，引进如下概念。

定义1［1］设函数f：Rn→R∪｛+∞｝，如果对于任意的x，有：

（i）f（λx）=λ（fx），则称函数f 具有正齐次性；

（ii）f（x+y）≤f（x）+f（y），则称函数f 具有次可加性。

定义2［6］函数f：Rn→R∪｛+∞｝，如果对于任意的λ∈（0，1］，有：

（i）f（λx）≤λf（x），则f 称为radiant 函数（一类特殊的抽象凸函数）；

（ii）f（λx）≥λf（x），则f 称为co-radiant函数（一类特殊的抽象凹函数）。

定义3［7］一个集合E⊆Rn被称为是近似凸的，如果存在一个集合C⊆Rn，使得

文献［1，8］给出了回收锥的如下性质。

引理1［1］设线性变换A：Rn→Rm以及Rm中的闭凸集C，且满足A-1C≠Ø，则

引理2［8］设C⊆Rn为一非空凸集，则

实际上，对于任意给定的x∈riC，有

2 回收锥和回收函数的性质

首先，我们考虑回收函数和广义回收函数的正齐次性、次可加性和抽象凸性。

定理1设f：Rn→R∪｛+∞｝为线性泛函，则对于任意的λ＞0，有

即rf为正齐次函数。

证明任取λ＞0，则

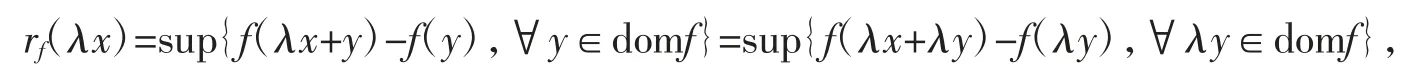
由于f 为线性泛函，故f（λx+λy）-f（λy）=λf（x+y）-λf（y），则有

从而结论成立。

定理2设f：Rn→R∪｛+∞｝为线性泛函，则对于任意的y∈dom f，有

证明任取x，y∈dom f，则由等价定义可知，rf（x+y）=sup｛f（z+x+y）-f（z），z∈dom f｝，由于f 为线性泛函，故f（2z+x+y）=f（z+x）+f（z+y），则有

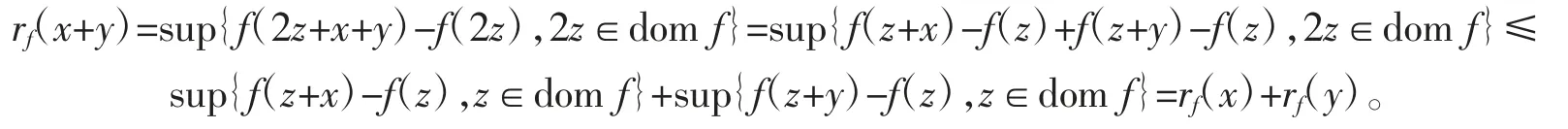
从而结论成立。

文献［3］给出如下广义回收函数的概念。

定义4［3］设函数f：Rn→R∪｛+∞｝为有限函数，f 的广义回收函数fO+是由f 的上图epi f 的广义回收锥产生的函数，即

与定理1 和定理2 的证明类似可建立如下性质。

定理3设函数f：Rn→R∪｛+∞｝为有限函数，则

证明对于任意x∈Rn，（x，v）∈

定理1中线性条件必不可少。

例如：f 为radiant 函数，不能得出rf（λx）≤λrf（x）。即存在y∈R，使得

例1 y=x2。

证明任取λ∈（0，1］，f（λx）=（λx）2=λ2x2≤λx2=λf（x），则f（x）为radiant 函数。

例如：f 为co-radiant 函数，即存在y∈R，使得

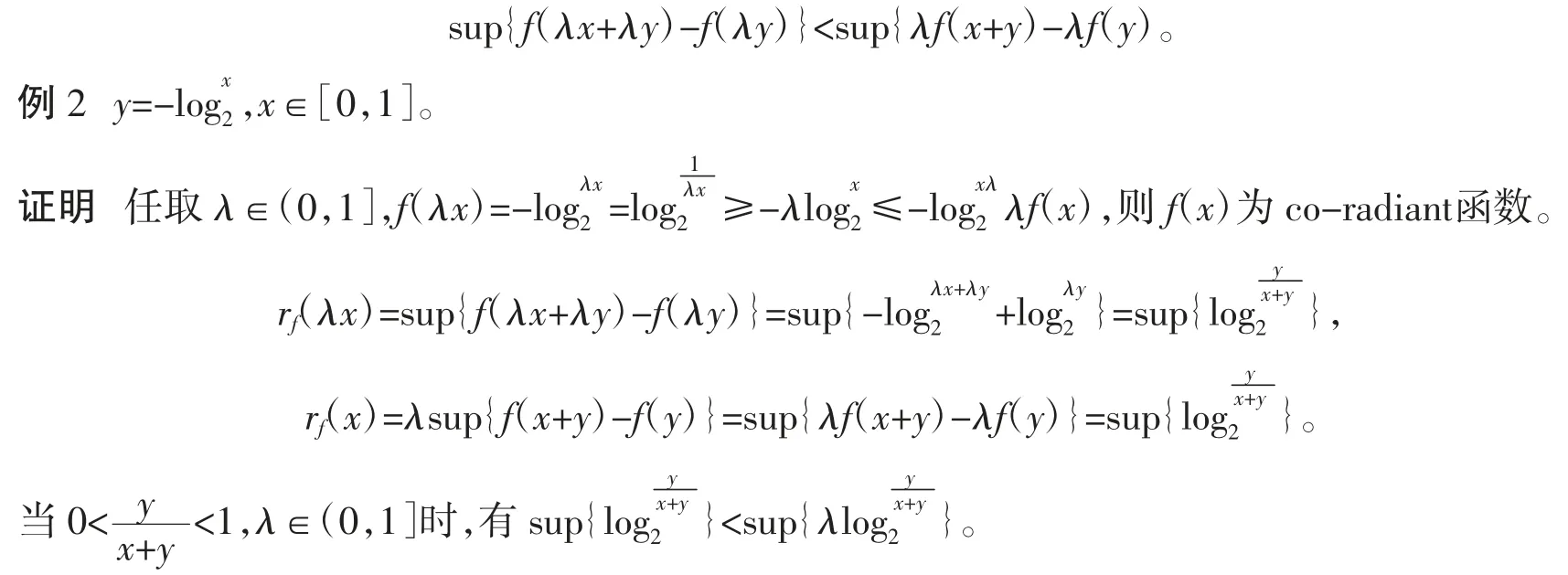
定理4凸集C⊆Rn，线性变换A：Rn→Rm，有

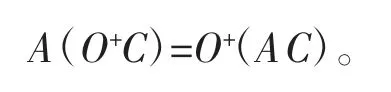
证明对于任意y∈A（O+C），存在z∈O+C，使得y=Az，而z∈O+C，说明对于任意x∈C 和λ＞0，x+λz∈C。于是有Ax+λAz=Ax+λy∈AC，得出y∈O+（AC）。

反包含不一定成立，因为线性变换不一定可逆，所以Ax+λAz∈AC 不能得出x+λz∈C。

例3

即O+（AC）⊄A（O+C）。

定理5设C⊂Rn为一非空近似凸集，则

证明C 为近似凸集，则riC，clC 为凸集，对任意给定的x∈riC，有

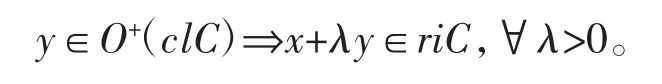
则结论成立。

例如：当

即O+（riC）=O+（clC）。

3 结语

本文研究了回收锥和回收函数的一些性质，在文献［5］回收锥和文献［4］回收函数的相关性质下，针对回收锥和回收函数作了进一步的研究，首先，得出了在线性条件下回收函数满足正齐次性和次可加性，并通过例子说明若函数不具备线性条件，函数的回收函数是不满足正齐次性的；其次，得出了回收锥在线性变换中，不存在相互包含的关系，并通过例子说明了其合理性；最后，得出若将定理中的凸性条件弱化为近似凸，其相对内部的回收锥和闭包的回收锥仍然相等的性质。