新型双层Halbach永磁单元建模与仿真研究

2021-12-07袁亚强王战中

石家庄铁道大学学报(自然科学版) 2021年4期

袁亚强，王战中，赵童

(石家庄铁道大学机械工程学院，河北石家庄 050043)

0 引言

随着特种机器人的技术不断发展，爬壁机器人因其自身不仅可以在水平壁面上工作，也可以在倾斜或垂直壁面上工作，故其应用领域越来越广泛。在风力发电柱维护、大型油罐检测、船舶清洁等任务中，经常采用磁吸附爬壁机器人进行相关作业。

吸附能力是爬壁机器人最基本的也是最重要的因素。根据吸附方式的不同，可以将爬壁机器人分为磁吸附、真空吸附、仿生吸附等类型。其中磁吸附爬壁机器人应用较为广泛，磁吸附又分为电磁吸附和永磁吸附2种方式。而永磁吸附由于吸附力大，吸附稳定，所以能更好地适应各种工作状况，应用也较为广泛。钟华等[1]通过实验及分析得到同极对接的磁体产生的磁场强度是单个磁体产生的2倍。薛珊等[2]设计了一种同极对接阵列磁体，在对接磁铁间和两侧放置导磁轭铁，用于引导磁感线，在结构的上侧放置隔磁材料，减少上侧漏磁，从而提高吸附效率。桂仲成等[3]对传统乙型磁路进行了设计和优化，通过对磁体各尺寸的分析和优化得到最优磁路，并根据应用环境设计了吸附单元的最优布局。陈勇等[4]、沈青青等[5]为减少传统的Halbach阵列磁路的漏磁现象，在磁路结构中加入软铁，并通过改变吸附装置与吸附壁面的角度控制磁吸附力的大小。闫晨飞等[6]提出了一种变磁化方向的永磁吸附结构，相较之前的磁吸附力得到了有效提高。但是该装置由不同磁化方向的磁体紧密组合而成，结构复杂，制作困难。赵童等[7]对相同磁体数量不同布局方式进行研究，得到了最佳布局方式和理想工作间隙。

结合之前永磁吸附的研究，提出一种新型双层Halbach永磁阵列吸附单元，并采用Ansoft Maxwell软件对吸附单元的磁场强度和吸附力进行仿真分析。通过分析不同结构尺寸对吸附性能的影响，进而对磁吸附单元进行优化，提高磁吸附性能。

1 磁吸附单元的磁路设计

美国学者Klaus Halbach于1979年提出了一种新的磁体排列结构，即Halbach结构，该结构通过将不同充磁方向的永磁体进行排列，以使得磁力线在一侧进行加强，另一侧进行削弱。其原理如图1所示。

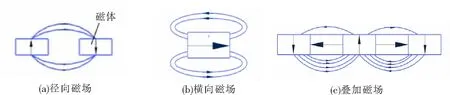
图1 Halbach阵列原理图

如图2所示，为了更好地产生聚磁效应和减少Halbach结构的漏磁问题，陈勇等[4]、沈青青等[5]在传统Halbach结构中增添软铁以引导磁力线，有效减少了弱磁侧的漏磁问题，并且使强磁侧和壁面之间的气隙磁通密度呈周期变化。

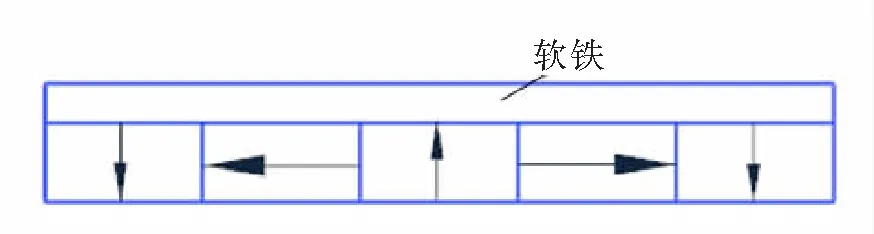
图2 改进Halbach阵列图

本文所提出的新型双层吸附单元如图3所示，箭头代表充磁方向。上层为一对同极对接的磁体，中间为竖直向上充磁的磁体。下层由直线型Halbach永磁阵列组成。下层的Halbach永磁体产生聚磁和弱磁磁路，上层同极对接的磁体引导磁力线，减少漏磁，增大磁吸附性能。其中H为上层磁体厚度，T为下层磁体厚度，A1为竖直向下充磁的磁体长度，A2为水平方向充磁的磁体长度，A3为竖直向上充磁的磁体长度。

图3 新型双层Halbach永磁阵列图

吸附装置中的永磁体材料采用稀土永磁材料汝铁硼(NdFeB)。选用系列中的N35作为永磁材料，其性能参数[8]如表1所示。

表1 NdFeB N35性能参数

2 吸附单元磁吸附力计算

2.1 数学模型建立

二维静态磁场的麦克维斯方程组[9]为

(1)

式中，H为磁场强度；J为电流密度；B为磁感应强度。由于此属于静磁场问题，故式(1)可简化为

(2)

对于场量B、H之间的关系由介质的特性决定，由于吸附装置中介质是各向同性的，故有：B=μH,其中，μ为介质的磁导率。

根据库伦规范有

A=0

(3)

由式(1)～式(3)可以得到

(4)

在整个求解域中应满足方程

(5)

式中,O为整个有效域；S为永磁束缚电流J的界限；L1为不同介质的交界线；L2为磁力线的边界。

2.2 吸附单元吸附力计算

当工作间隙Lg(如图4所示)较小时，将吸附单元与壁面之间的气隙沿长度方向均分为n份，每份所产生的磁吸附力Fi[4]为

图4 有限元结构模型

(6)

式中,Bi为每份磁感应强度；Si为每份气隙面积。

则磁吸附单元所产生的磁吸附力F为

(7)

式中,Bg为气隙磁感应强度；Sg为工作间隙总面积。

而气隙磁感应强度由磁通连续原理和安倍原理[11]可得

(8)

式中，BmHm为磁能积；Vm为永磁体体积；Vg为气隙体积；σ为漏磁系数;f为磁路的磁阻系数。

由式(6)～式(8)得

(9)

由式(7)可知，气隙磁感应强度和气隙面积对磁吸附力有重要影响。而永磁体体积、空隙体积、漏磁系数、磁阻系数、磁能积对气隙磁感应强度具有重要影响，且这些值受结构的尺寸影响。因此，改变结构尺寸对磁吸附力具有重要影响。

3 有限元分析及参数优化

3.1 有限元模型建立及分析

如图4所示，利用Ansoft Maxwell软件建立二维静态磁场模型。其中取上层磁体厚度H=5 mm，下层磁体厚度T=10 mm，A1=A2=A3=10 mm，工作间隙Lg=5 mm。

磁吸附单元有限元分析中涉及的材料有永磁体、吸附壁面、气隙。永磁铁选用汝铁硼N35，相对磁导率为1.099 778 5；工作间隙为空气，相对磁导率为1；吸附壁面采用纯铁，相对磁导率为4 000。

在保证相同结构参数的前提下，对传统Halbach永磁阵列模型和新结构模型进行对比分析。图5(a)、图5(b)分别为2种磁路模型的磁力线分布图。由图可知，传统模型利用软铁减少了弱磁侧漏磁，但未改变其端部漏磁。新型磁路模型下层用Halbach磁路结构产生强磁侧和弱磁侧，上层通过同极对接的磁体产生双倍磁场强度并且对磁力线进行引导，使得更多的磁力线通过上层磁铁引导后聚集到工作间隙中，从而减少漏磁现象，很好地改善了端部漏磁问题。图5(c)、图5(d)分别为2种磁路产生的磁吸附力，传统磁吸附力为5 278.4 N，新型磁路模型的磁吸附力为7 184.7 N，磁吸附力提高36%，提高了其磁力吸附能力。

图5 2种模型对比图

3.2 吸附单元的结构参数分析

通过控制单一变量的方法，研究吸附单元结构各尺寸对磁吸附力大小的影响。

3.2.1 上层磁铁厚度H对磁吸附力的影响

取T=10 mm，A1=A2=A3=10 mm，通过改变H的大小研究磁吸附力大小的变化。H的变化范围取1～30 mm，步长为1 mm。将仿真计算的数据导入到Origin软件进行处理，得到磁吸附力随H变化的曲线(图中黑色方块连线)，如图6所示。由图6可知随着上层磁铁厚度H的增加磁吸附力F也随之增大。上层磁铁厚度H从1 mm逐渐增加到15 mm时，磁吸附力迅速增加；而H从15 mm增加到30 mm时，虽然磁吸附力F也逐渐增加，但是变化比较平缓。H从15 mm增加到30 mm，厚度增加了50%，而磁吸附力从9 709.2 N增加到11 428 N仅增加了17.7%左右，即永磁体的利用率不高。原因是因为随着H的逐渐增加，上层同极对接磁体产生的磁力线有一部分不能通过下层磁路传到工作间隙中。虽然H增加，但下层所产生的磁力线不变，故上层磁路参与引导下层磁力线的磁铁体积会逐渐增加，将所有磁力线引导后，新增的上层磁体不再参与引导，造成了磁力浪费。故在满足磁吸附要求的前提下，上层磁体厚度不应过大。下层磁铁厚度T=10 mm时，上层磁体厚度H取5～10 mm之间,磁吸附力效率较高。综合考虑，上层磁铁厚度与下层磁铁厚度的比值H/T应在0.5～1之间为宜。

图6 磁吸附力随H变化曲线与拟合曲线

根据仿真计算的数据，利用Origin软件对其进行拟合，得到拟合曲线(见图6)和数值解析表达式(10)。从拟合曲线中可以看出当H>30 mm时，磁吸附力虽然随着H的增加而增大，但增加幅度较小，与上述磁吸附力变化曲线一致。其数值解析表达式为

(10)

3.2.2 下层磁铁厚度T对磁吸附力的影响

取H=5 mm，A1=A2=A3=10 mm，通过改变T的大小研究磁吸附力大小的变化。T的变化范围为1～30 mm，步长为1 mm。将仿真计算的数据在Origin软件中绘制成曲线图(图中黑色方块连线)，如图7所示。随着T逐渐增加，磁吸附力F也逐渐增大，在1～12 mm之间吸附力F变化较大，而在12～30 mm之间吸附力F变化比较平缓，且在20～30 mm之间磁吸附力基本保持不变。当T从10 mm变化到20 mm时，磁吸附力F从7 158 N变化到9 089 N，磁铁体积增加一倍，但磁吸附力仅提高了26.9%。随着T逐渐增加，吸附力F增加较为缓慢，是因为工作间隙中的磁通逐渐饱和。当气隙磁通达到饱和状态时，增加T对磁吸附力影响较小，且会造成磁浪费和增加装置质量。故T的取值范围应在8～12 mm之间。

图7 磁吸附力随T变化曲线与拟合曲线

根据仿真计算的数据，利用Origin软件对其进行拟合，得到拟合曲线(见图7)和数值解析表达式 (11)。从拟合曲线中可以看出，当T>30 mm时，随着T的逐渐增大，磁吸附力基本保持不变，此时T对磁吸附力影响较小。其数值解析表达式为

F=10 076.498-8 560.954×(0.895)T

(11)

3.2.3 磁体长度A3对磁吸附力的影响

为研究A3对吸附力F的影响，保持H=5 mm，T=10 mm，A1=A2=10 mm不变，A3取1～30 mm，步长为1 mm，研究吸附力F的变化。将仿真计算的数据导入到Origin软件进行处理，得到吸附力随A3变化的曲线(图中黑色方块连线)，如图8所示。从图8中可以看出,吸附力F随着A3的增加逐渐增大。在1～15 mm之间吸附力F变化较大，而在15～30 mm之间吸附力F变化较小。这是因为竖直向上充磁的磁体所产生的磁力线是通过左右水平充磁的磁体、向下充磁的磁体、气隙、工作壁面形成闭合磁路，当A3逐渐增加时，两侧磁铁和气隙之间的磁力线达到饱和状态，再增加A3，磁吸附力F变化不明显。为提高磁吸附效率，在磁体长度A1=A2=10 mm时，A3应取10～15 mm之间。即A3/(A1+A2)应在0.5～0.75之间。

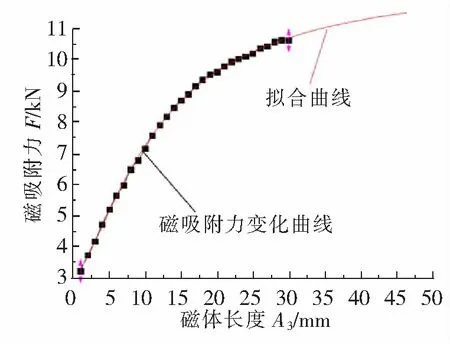
图8 磁吸附力随A3变化曲线与拟合曲线

利用同样的方法，在Origin软件中得到拟合曲线(见图8)和数值解析表达式(12)。从拟合曲线中可以看出当A3>30 mm时，磁吸附力虽然随着A3的增加而增大，但变化比较平缓。其表达式为

F=11 838.532-99 343.966×(0.931)A3

(12)

3.2.4 磁体长度A1、A2对磁吸附力的影响

取H=5 mm，T=10 mm，A3=14 mm，并保持A1+A2的总值为20 mm，研究A1、A2在0～20 mm之间以1 mm作等距变化过程中磁吸附力F的变化情况。按照上述方法在Origin软件中绘制出磁吸附力随A1、A2变化的曲线(图中方块连线)，如图9所示。从图9中可以看出，随着A1、A2的变化，磁吸附力F也随之变化。在A1从0增加到6 mm，A2从20 mm减少到14 mm时，磁吸附力F随之增大；A1和A2继续变化，磁吸附力F逐渐减小。当A1从0逐渐增加时，竖直向下充磁的磁体将上层磁体产生的磁力线进行引导，使之汇聚到工作间隙中，但是在A1逐渐增加的过程中，A2逐渐减小，而随着A2的减小，下层Halbach阵列磁路所产生的的强磁和弱磁现象减弱，故导致整个吸附单元的吸附力逐渐减小。分析A1=5 mm，A2=15 mm时磁吸附力达到最大。即A1∶A2为1∶3时，整个吸附单元的吸附力最大。

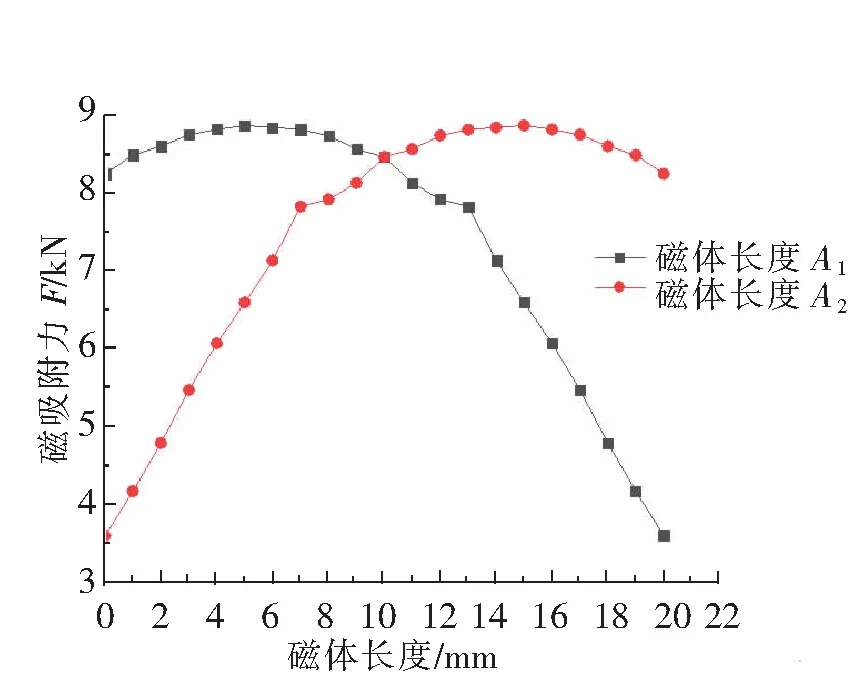
图9 磁体长度A1、A2对磁吸附力的影响

由于A1、A2对磁吸附力变化影响曲线对称，故只对A1进行4次多项式曲线拟合。其拟合曲线如图10所示，其数值解析表达式为

图10 磁吸附力随A1变化曲线与拟合曲线

(13)

3.2.5 工作间隙长度Lg对磁吸附力的影响

基于以上分析，取H=5 mm，T=10 mm，A1=4.5 mm，A2=13.5 mm，A3=14 mm，在此基础上研究工作间隙对磁吸附力大小的影响。取工作间隙范围为0～30 mm，步长为1 mm。按照同样的方法将仿真数据在Origin软件中绘制成磁吸附力随Lg变化的曲线(图中黑色方块连线)，如图11所示。从图11可以看出，随着气隙的不断增大，磁吸附力逐渐降低。气隙在0～3 mm时吸附力急速下降，在3～10 mm时气隙对吸附力的影响趋于稳定，当气隙长度为15 mm时，吸附力近乎为0。由图11可知,气隙长度是影响吸附力的重要因素，故在设计吸附单元时要充分考虑气隙对吸附力的影响。

图11 磁吸附力随Lg变化曲线与拟合曲线

按照上述方法，在Origin软件中得到拟合曲线(见图11)和数值解析表达式(14)。从拟合曲线中可以看出，当Lg>20 mm时，磁吸附力接近于0。其表达式为

(14)

3.3 结构尺寸优化分析

在研究吸附单元各结构尺寸对磁吸附力大小影响的基础上和保证吸附单元的体积不变的前提下，为了得到最优的结构参数，对吸附单元各结构尺寸设定变量范围。对上层磁体厚度H(4～10 mm)、下层磁体厚度T(8～12 mm)、下层磁体长度A1+A2(16～23 mm)、A3(8～17 mm)，即磁体总厚度(12～22 mm)，磁体总长度(40～63 mm)，进行优化分析，得到磁吸附力变化曲线，如图12所示。从图12可以看出，通过保持体积不变，对吸附单元的结构尺寸进行优化分析，当磁体总长为58 mm，磁体总厚度为12.9 mm，即H=4.3 mm，T=8.6 mm，A1=5.6 mm，A2=16.7 mm，A3=13.4 mm时，吸附力达到最大为8 363.1 N。

图12 结构参数对吸附单元磁吸附力的影响

基于上述优化结果对磁体总长为58 mm，磁体总厚度为12.9 mm(即A1=5.6 mm，A2=16.7 mm，A3=13.4 mm，H=4.3 mm，T=8.6 mm)的新型磁路结构和传统Halbach磁路结构在Ansoft Maxwell软件中进行分析比较，得到如图13(a)、图13(b)所示的传统磁路和新型磁路的磁力线和磁感应强度分布图。从图13可以看出,新型磁路结构的磁力线和磁感应强度更加集中在工作间隙中，能够明显提高磁吸附能力。

图13(c)、图13(d)为气隙5 mm时传统Halbach磁路模型和新型双层Halbach模型的磁吸附力。由图13可知,传统Halbach磁路模型磁吸附力为5 566.3 N，新型磁路模型的磁吸附力为8 363.1 N，磁吸附力提高了2 796.8 N，提高率为50.25%。