基于皮尔森算法的无线网络指标相关性判断方法

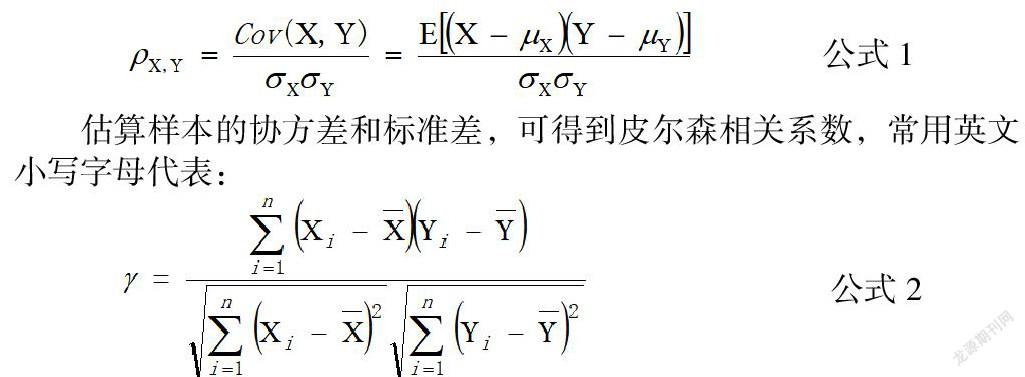
摘要：面向大量用于描绘无线网络性能的指标，该论文提出了一种以皮尔森算法为核心的指标关联性判断方法。该方法基于皮尔森相关系数构建算法，采用降维、相关性计算、加权、聚类等数据处理手段，并制成相应分析工具，在覆盖、容量、干扰三大根因组合的多场景下，指出根本问题，为优化人员提供了优化方案选取思路，能有效指导异构网的优化工作。

关键词：无线通信;皮尔森相关系数;指标;网络优化

1.背景

在无线网络优化工作中，面对的往往是复合型问题，仅仅依靠单一的指标优化，很难对实际问题进行有效的、准确的、全面的解决，优化方案偏离靶心，治标不治本。

现有优化指导策略提供的大多是基于单一指标的优化思路，如VOLTE高掉话问题，大部分指导书只会说明若是覆盖问题引起就如何处理、若是干扰引起如何处理，缺乏指标间的关联、降维体系，引导复合型网络问题的解决。

2.目前存在的问题

目前主流优化方式主要存在以下两点问题。

2.1.现有优化方式缺乏复合型问题分析指引

现有方法大多是从某项网络指标的优化出发，叙述此项指标从各方面如何优化。但现网存在大量的“复合型”网络问题，即多项指标存在恶化，在此情况下，必须有效梳理指标间关联性，现有优化指导方案不能达到此目的。

2.2.现有优化方法缺乏根因指标关联分析

在网络优化工作中，我们将覆盖、容量、干扰定义为网络问题的根因指标，其他指标恶化为根因指标出现问题引发的上层问题，为“表象”。现有方法在仅针对某项指标，探讨其由覆盖、容量、干扰引起时应该如何处理，缺乏上层指标与根因指标之间的关联性分析，导致关联性差，优化精准度低，难以真正对接生产一线。

3.皮尔森算法的原理论述

为解决此关联性问题，本论文引入统计学中皮尔森相关系数（Pearson correlation coefficient，又称皮尔森积矩相关系数）用于表征网络指标间相关性。

3.1.皮尔森相关系数简介

两个变量间的皮尔森相关系数定义为两个变量间的协方差和标准差的商：

估算样本的协方差和标准差，可得到皮尔森相关系数，常用英文小寫字母代表：

值介于-1和1之间，当两个变量的线性关系增强时，相关系数趋于1或-1;当一个变量增大，另一个变量也增大时，表明它们之间是正相关的，相关系数大于0;如果一个变量增大，另一个变量却减小，表明它们之间是负相关的，相关系数小于0;如果相关系数等于0，表明它们之间不存在线性相关关系。

3.2.皮尔森相关系数适配性讨论

统计学一般认为，皮尔森相关系数通用约束条件为：

（一）两个变量间有线性关系;

（二）变量是连续变量;

（三）变量均符合正态分布，且二元分布也符合正态分布;

（四）两变量独立。

网络性能指标满足以上1、2、3点，而第4点可通过指标间类别划分达成彼此独立。因此网络性能指标与皮尔森相关系数的约束条件高度吻合，可利用皮尔森算法可以挖掘各项指标间的相关性，从而进行覆盖、容量、干扰三个维度的根因指标相关性提取以及对其他类的数据清洗，确定根因，引导优化策略制定。

4.以皮尔森算法为核心的指标关联体系

以皮尔森算法为核心，本论文提出一套挖掘指标相关性的关联体系。

4.1.皮尔森系数实现

借助Python通过函数调用可实现指标两两之间皮尔森相关系数计算。

4.2.加权及聚类实现

简易算法描述如下：

（一）对小区的全量指标进行筛选，找出问题指标，如小区A问题指标集{a1、a2、a3……};

（二）将每个问题指标与覆盖、容量、干扰根因指标的皮尔森相关系数进行加权计算（Correlation×Weight），分别求出每项指标对应覆盖、容量、干扰的分数，如问题指标a1对应分数为FG1、RL1、GR1;

（三）将问题指标与三大网络问题类型进行关联后，分数最大表示相关度最高，如问题指标a1的FG1最大，代表主要由于覆盖问题造成a1指标恶化;

（四）根据各项问题指标计算得到的分数进行求和，得到覆盖、容量、干扰的总分（ FG=FG1+FG2+……+FGn，RL=RL1+RL2+……+RLn，GR=GR1+GR2+……GRn），对比后总分最大的项为问题小区的主要网络根因。

至此，完成了一套以网元小区各项网络指标为输入、通过以皮尔森算法及加权计算为内核进行数据处理、输出与问题小区众多指标最相关根因指标的关联系统。

5.输出结果与试点情况

5.1.输出结果

指标关联体系输出的覆盖、干扰、容量3个维度根因指标的加权组合，共可穷举25种组合，其中单一场景3种，复合场景22种。

通过对某地级市全量小区进行指标关联，得出3种单一场景（弱覆盖、高干扰、高流量）现网问题点占比约79%，表示约79%的小区仅在一项根因指标出现问题。剩余约21%为复合型场景，即两类根因的复合、三类根因的复合。

5.2.试点案例

某市网络问题小区A，在半年期间频繁出现弱覆盖、VoLTE切换差、下行低速率、高资源利用率等网络问题，而回溯问题处理记录，分析人员认为此问题主要是以解决VoLTE切换差为主，提出优化解决方案，大部分指标没有显著改善。

通过指标关联体系工具进行单点分析发现，该网络问题小区的覆盖、容量根因指标均存在问题，且与覆盖综合打分更高，即上层指标变化与覆盖情况变化相关性更强，依此结论进行了优化覆盖为主、容量问题为辅的调整策略，效果显著。

6.总结与展望

基于皮尔森算法的无线网络指标关联性判断方法能够较为有效地处理应对“复合型”网络问题，将“上层”网络指标问题向“根因”网络指标映射，并形成工具，智能输出处理建议，便于优化人员制定方案。目前本算法已在用户感知指标的挖掘中初步应用，并在日常无线网络优化工作中得到良好试用普及。

参考文献

[1]中国移动通信集团广东有限公司无线网优中心，1+N集中优化白皮书–V4.0[S]

[2]尹欢一，文志诚，马正见.一种基于皮尔森相似度和距离权重的改进KNN算法[J].电脑知识与技术，2019，15（27）：208-210.

作者简介：黄琰奕，（1991.8 -），男，江西省鹰潭市，汉族，本科，中级工程师，长期从事无线网规划、优化及其新技术的研究与实践。