K-means算法及其应用实践

2021-12-06张松慧

科学与生活 2021年23期

摘要：机器学习分为监督学习和无监督学习，无监督学习一个非常重要的用途就是对数据进行聚类。聚类算法则是在完全没有标签的情况下，算法“猜测”哪些数据应该聚为一类。K-means算法是被广泛应用的一种聚类算法，K-means算法的关键是选择合适的k值，文章通过鸢尾花聚类展示K-means算法应用。

关键词：K-means算法;聚类;无监督学习;机器学习

一、何为聚类

聚类（Clustering）是一种典型的“无监督学习”。聚类算法是对大量未知标记的数据集，根据数据之间的距离或者说是相似性（亲疏性）将数据集划分为多个簇（Cluster），使簇内的数据相似度尽可能大，而簇间的数据相似度尽可能小。

聚类的目的是把数据分类，但是事先我们不知道如何划分，即聚类的类别和数目没有预先的定义，是根据数据点的相似性（即数据点之间的距离）来划分的。

聚类与分类最大的区别是：聚类为无监督学习，待处理数据没有任何先验知识，而分类是有监督学习，即存在先验知识的训练数据集。

二、K-means聚类算法原理

K-means算法也称为k均值算法，由于其简洁和效率，成为所有聚类算法中应用最为广泛的一种聚类算法。对于给定的样本集，按照样本之间距离的大小，将样本集划分成k个簇，让簇内的数据点尽量紧密地连接，而簇与簇之间的距离尽量大。k是簇的个数，k由用户指定，每个簇中所有点的中心称为质心，k均值算法根据某个距离函数反复把数据分入k个簇中。

K-means聚类算法的工作原理是：先随机选取k个点作为初始的聚类中心，然后针对每个数据点，计算每个点与各个聚类中心之间的距离，把每个点归为距离它最近的聚类中心代表的簇类。一次迭代结束之后，重新计算每个簇类的中心点，然后针对每个点，重新寻找距离自己最近的中心点。如此循环，直到前后两次迭代的簇类没有变化。

终止条件可以是以下任何一个：

（1）没有（或最小数目）对象被重新分配给不同的聚类。

（2）没有（或最小数目）聚类中心再发生变化。

（3）误差平方和局部最小。

三、K-means算法流程

K-means算法是一个反复迭代的过程，算法的基本步骤为：

步骤1：选定要聚类的类别数目k，随机选择k个中心点（质心）。

步骤2：针对每个样本点，找到距离其最近的中心点（寻找组织），距离同一中心点最近的点为一个类，这样完成了一次聚类。

步骤3：判断聚类前后的样本点的类别情况是否相同，如果相同，则算法终止，否则进入步骤4。

步骤4：针对每个类别中的样本点，计算这些样本点的中心点，当做该类的新的中心点（即将每个类别中所有对象所对应的均值作为该类别的聚类中心点），继续步骤2。

上述步骤的关键两点是：1. 找到距离自己最近的中心点。2. 更新中心点。

常用的距离度量标准是欧几里得距离的平方：

四、K-means算法中K值的选择

K-means算法中的k值需要预先确定，k值设为几即聚几类。在实际应用中k值是非常难以选择的，通常的做法是多尝试几个k值，看聚成几类的结果更好解释，更符合分析目的等。

还可以采用“肘”方法（Elbow method）确定k值。该方法的原理就是最小化点到聚类中心的距离。

“肘”方法的步骤：

（1）对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和;

（2）平方和是会逐渐变小的，直到k==n时平方和为0，因为每个点都是它所在的簇中心本身;

（3）在这个平方和变化过程中，会出现一个拐点也即“肘”点，下降率突然变缓时即认为是最佳的k值。

一般来说，手肘图都会展现出一个肘部轮廓，下降率突然变缓时即认为是最佳的k值。

随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么簇内距离平方和自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故簇内距离平方和的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以簇内距离平方和的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说簇内距离平方和和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。

五、K-means算法实现鸢尾花数据的聚类

任務目标：使用scikit-learn内置的鸢尾花数据集，该数据集每条记录都有4个特征：花萼长度（calyx length）、花萼宽度（calyx width）、花瓣长度（petal length）、花瓣宽度（petal width），通过这4个特征可以预测鸢尾花属于哪一品种。我们选取数据的后两个特征，即花瓣长度和花瓣宽度作为训练数据，首先根据绘制的鸢尾花数据分布图查看数据分分布情况，然后绘制出手肘图，进一步辅助确定合理的k值。

步骤一：选取鸢尾花数据集的后两个特征即花瓣长度和宽度，绘制出鸢尾花数据分布图，如图1所示。

从鸢尾花数据分布图可以大致看出鸢尾数据的分布情况。

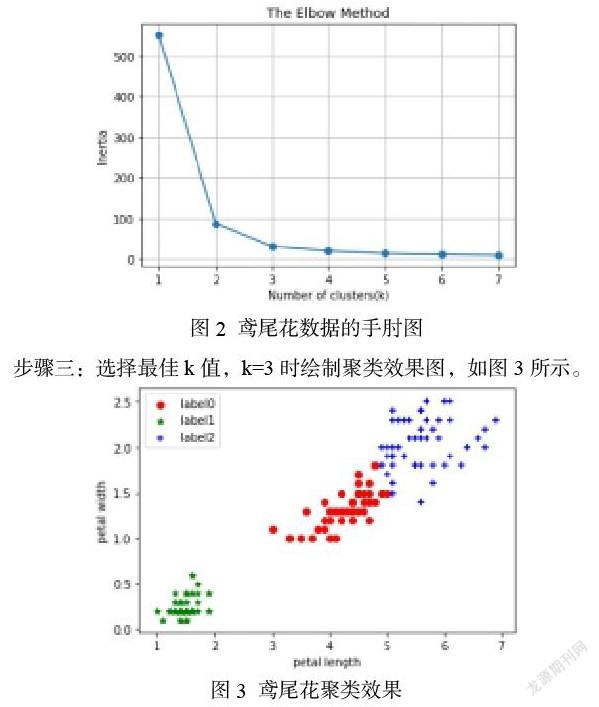
步骤二：绘制出分类数1到7时，分类数（k）和簇内距离和inertia的对应关系图，即手肘图，如图2所示。

观察图中各点的曲率可以看到，k=3之后，簇内距离平方和inertia的下降变得很缓慢了，因此最佳的k值为3。

步骤三：选择最佳k值，k=3时绘制聚类效果图，如图3所示。

3个类别的鸢尾花数据分别用绿色的五角星、红色的圆点和蓝色的+号表示，可以看到k=3时的聚类效果很好。

六、总结

聚类用于数据集内种类属性不明晰，希望通过数据挖掘或自动归类出有相似特点的对象的场景。K-means算法可用于维数、数值都很小且连续的数据集，比如在市场营销领域，建立合理的客户价值评估模型，对客户进行分群，分析不同客户群的客户价值，从而制定相应的营销策略，对不同的客户群提供个性化的服务等。

K-means算法原理比较简单，实现也很容易，收敛速度快，聚类效果也比较好，算法的可解释度比较强，主要需要调参的参数是簇数k。但k值的选取不好把握，本文采用绘制手肘图的方法辅助选取最佳的k值。

参考文献

[1] 钟志峰，李明辉，张艳.机器学习中自适应k 值的k 均值算法改进[J].计算机工程与设计，2021，42（1）：136-141.

[2] 李玥.机器学习的分类、聚类研究[J].电脑知识与技术，2020，16（4）：161-162.