空间向量在高中数学问题解决中的应用

李波

摘要：向量是数科学领域中一个非常重要的概念和工具。这为高中生解决一些复杂的数学问题提供了一条新的途径。它可以帮助简化解决问题的过程，避免大量重复计算，并提高解决问题的准确性和效率。因此，如何才能有效地加深我们中学生对这一矢量的理解和理解。如何提高我们利用载体解决中学实际问题的能力，是一个值得深入探讨的问题。

关键词：空间向量;高中数学：应用

前言

在高中数学计算以及几何中，将大量应用于矢量知识点。矢量的最大特点是将抽象与形象思维相结合，使抽象的知识更直观，从而提高学生的理解能力。数学作为一门复杂的学科，不仅要求学生具有一定的理解能力，而且要求学生具有逻辑思维能力，因此矢量成为一种有效的学习工具。采用矢量解法不仅可以使枯燥的数学问题变得简单，而且可以使学生的解题过程更易于操作。

一、向量的内容和特点

矢量起源于物理学，应主要用于数学中的几何学。经过长期的研究，学者们开始将向量与空间相结合，使向量在数学中得到了更广泛的应用。目前，矢量有多种，如单位矢量、自由矢量等，矢量的运算也有多种。因此，我们可以看到矢量在数学中被广泛使用。当然，定向量不仅好，而且存在一些缺陷。首先，矢量的结构比较复杂。在高中数学的计算中，有时条件不适合矢量的应用。因此，矢量不是万能的解决方案，在运行过程中还需要对项目条件进行详细分析。其次，矢量的使用并不反映数学的本质。数学是一门非常严格的学科。如果我们在解决矢量问题时直接得到结果，那么学习的意义就会丧失。最后，当数学问题很难解决时，矢量的使用并不能减少问题的难度，反而会极大地增加计算量。因此，在认识矢量的过程中，应综合考虑矢量的优劣，采用辩证的方法来看待矢量的求解方法。

二、在解决平面几何问题中的应用

矢量不仅是尺寸的“定量”指标，也是方位角的“抽象”指标。这决定了它不仅能反映点或线之间的长度，而且还能直观地反映关系的位置。取决于差异的性质。矢量可分为零矢量、柯林和行数。通过分析矢量的性质，很容易发现矢量与平面几何中点和段的关系在大小和位置上有很强的相似性。因此，如果在求解平面几何问题的过程中引入矢量的概念，往往可以更快地找到求解数学问题的突破点。

例1，三角形ABC的三个顶点坐标分别是A（0，2），B（2，0）和C（1，3，1）。AB线、AC线和BC线的关键比分别为M线、N线和0线。

如果采用传统的方法，解决这个问题的过程是复杂的。如果能在这个时候巧妙地引入矢量知识，那么我们就能快速而清晰地解决这个问题。通过题目所给已知条件.可求出M.N和0三点的坐标为（一O.5，O.5）、（一1.5，一O.5）和（一3，1）。之后可求出MN直线方程在这种情况下，假设在MN上的点O的坐标是（x，Y），我们可以通过列出向量MN和N0之间的并行和共线关系来求解这个方程。同样地，HQ和N0的直线方程也可以用这种方法求解。

可以看出，将线段关系转换为矢量可以快速地解决这个问题。但在应用矢量知识解决平面几何问题的过程中。我们高中生必须明确点与线之间的关系，否则容易出现线段和矢量转换错误，最终导致问题的解决错误。

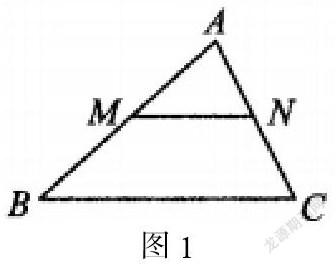
例2，如图1所示，点M是AB的中点，N是AC的中点，证明：MN//BC，同时2MN=BC.

结合“向量共线”思路进行求解.因为MN=AN-AM=1/2AB=1/2（AC-AB）=1/2BC.由此可知，MN与BC共线，IMNl=1/2IBCl.所以MN//BC且2MN=BC.

解析：通過使用向量共线的思想，不仅可以使解题效果得到进一步的优化，它能够使学生认识到向量方法，可以有效地解决数学问题，从而在今后的数学解题过程中更加主动地应用这种方法，使解题的速度以及解题的质量可以得到进一步的提高。

三、向量在立体几何问题中的应用

空间距离问题主要包括点线距、点面距、线面距、面面俱，如果使用几何的角度来进行这类问题的解决，就会要求学生要有非常高的空间想象力，并且这一解题过程过于复杂，而如果使用向量的方式可以使解题过程得到进一步的简化，同时对于空间响应能力的要求没有那么高，帮助学生可以更加高效快速地解决这类问题。

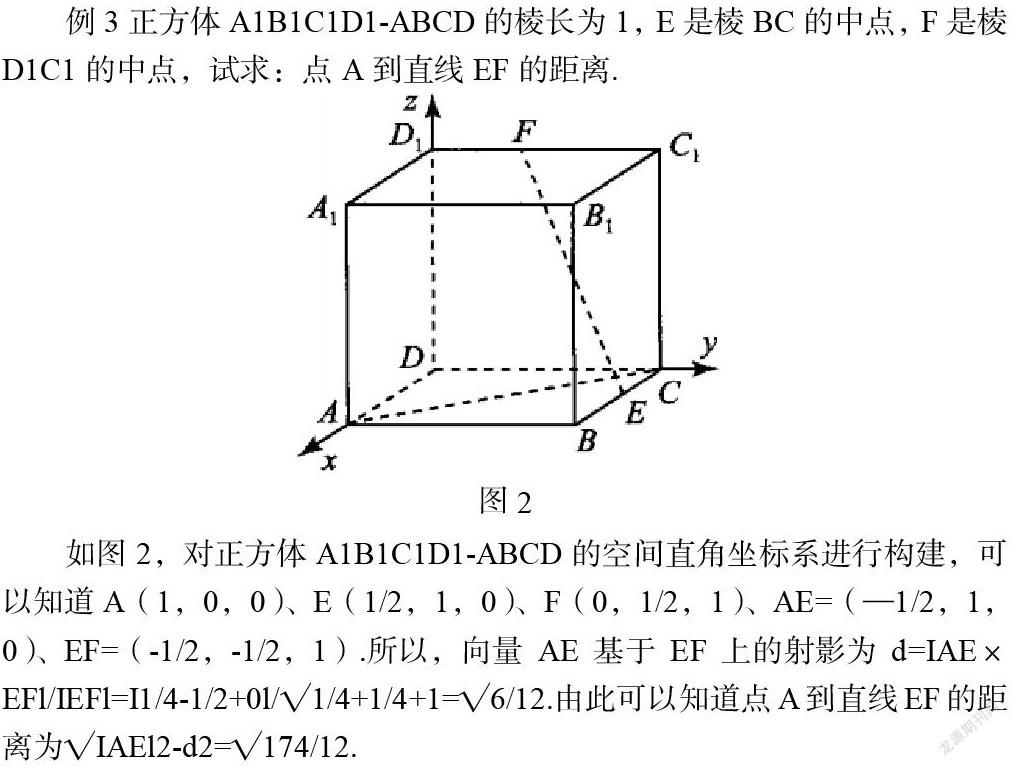
例3正方体A1B1C1D1-ABCD的棱长为1，E是棱BC的中点，F是棱D1C1的中点，试求：点A到直线EF的距离.

如图2，对正方体A1B1C1D1-ABCD的空间直角坐标系进行构建，可以知道A（1，0，0）、E（1/2，1，0）、F（0，1/2，1）、AE=（—1/2，1，0）、EF=（-1/2，-1/2，1）.所以，向量AE基于EF上的射影为d=IAE×EFl/IEFl=I1/4-1/2+0l/√1/4+1/4+1=√6/12.由此可以知道点A到直线EF的距离为√IAEl2-d2=√174/12.

四、结束语

矢量方差法不仅适用于上述问题，也适用于三角函数问题和离心率问题。向量方法在解决中、高中数学问题方面无疑是有用的，值得在教学中推广和应用。总之，矢量在中学数学教学中占有非常重要的地位，具有很强的实用性。这就要求教师在几何或三角函数中适当地运用它，才能恰当地运用到数学矢量，从而在一定程度上简化数学问题，在实际的高中数学课堂教学中，教师还需要对矢量的实际问题进行讨论和分析，同时提高解决问题的效率，提高教师的教学质量。向量在求解平面几何问题、解析方程问题、不等式证明问题等中高数学类型问题中的合理应用。它可以显着优化我们中学生解决相关数学问题的能力。快速找出问题的突破口是有帮助的，但也有必要关注实用数学问题的整合。综合矢量的特性和性质可以合理地改变相关项的已知条件，从而提高学生解决数学问题的能力。这也要求相关的，教师必须要重视教授学生使用相应的方法进行解决高中数学问题，使学生的数学成绩可以得到进一步的提升。

参考文献

[1]朱音.例谈向量方法在高中数学解题中的应用[J].长三角（教育），2012（7）.

[2]王晓.高中数学解题中向量方法的应用分析EJ3.高中数理化.2014（14）.

[3]刘永斌.向量在高中数学解题中的应用[J].吉林教育，2010（3）.