基于PNN的北斗转发式欺骗干扰信号检测方法

庞春雷，郭泽辉，吕敏敏，张 良，翟 丁，张 闯

（1.空军工程大学 信息与导航学院，西安 710077；2.95801部队，北京 100032；3.95510部队，贵阳 550025）

随着北斗卫星导航系统（Beidou Navigation Satellite System, BDS）应用的逐步深入，潜在的安全问题也渐渐暴露出来，由于卫星信号的脆弱性，致使导航接收机极易受到人为的欺骗干扰，严重影响定位结果[1,2]。欺骗干扰信号可以分为生成式和转发式两种[3]，其中转发式欺骗干扰无需进行码相关处理，通过对真实信号附加一定的时延后转发的方式，即可实现欺骗干扰的目的。相较于生成式欺骗干扰，转发式欺骗，结构简单，更容易实现，并且能够对P码产生影响，严重威胁导航定位的安全[4]。

准确检测出欺骗信号是有效抑制转发式欺骗干扰的重要前提[5]，在此基础上将欺骗信号与真实信号分类处理，避免欺骗信号影响定位解算。欺骗信号与真实信号最明显的区别在于空间分布上的差异，利用这一特性对接收信号进行检测是最为直接有效的方法[6,7]。文献[8]提出了基于双接收机伪距信息的转发式欺骗信号检测算法，需要借助接收机与卫星的精确位置信息实现欺骗检测，在应用上具有局限性。文献[9]提出利用双天线的载波相位差分观测值进行二元假设检验，并分析了相位双差算法对欺骗信号的误差来源；文献[10]在载波相位差分检测技术的基础上，提出利用方位变化的二元天线阵进行多次判决的方法，提高对欺骗信号的检测概率；文献[11]采用旋转天线的方式，降低了载波相位双差算法的检测盲区。上述利用载波相位差分的检测方法需要解算出整周模糊度[12],同时需要较长的观测时间来提高检验概率，难以满足实时检测的要求，并且检测性能受基线长度的影响，限制了应用范围。

转发式欺骗干扰的影响可以视为一种导航故障，当前深度学习被广泛用于故障诊断领域[13]，文献[14]提出利用狼群算法对欺骗信号进行参数辨识；文献[15]提出了基于监督机器学习的欺骗干扰检测算法。概率神经网络（Probabilistic Neural Network, PNN）是深度学习算法中常用的网络框架，具有结构简单、收敛迅速和分类准确率高的特点，在解决模式分类和故障判断方面具有独特优势[16]。因此，本文提出一种基于PNN的北斗转发式欺骗信号检测方法，在载波相位双差检测技术的基础上，通过建立PNN模型，利用双差观测值随时间变化的一致性特点，实现对欺骗信号的实时检测，并且根据检测结果分析并隔离欺骗干扰信号，最后通过实测数据验证了所提方法的有效性。

1 载波相位差分检测原理

正常情况下，北斗载波相位观测方程为：

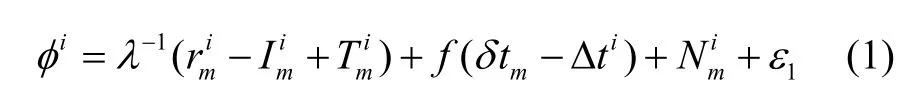
式中：上标i表示对第i颗卫星进行观测，下标m表示接收机m，λ表示载波波长，r表示接收机到卫星之间的几何距离，I、T分别表示电离层延迟和对流层延迟，δtm表示接收机钟差， Δti表示卫星钟差，N表示载波相位的整周模糊度，ε表示观测噪声。

在短基线的条件下，电离层延迟I和对流层延迟T的变化可以忽略，则接收机m和n之间的载波相位单差观测方程可以表示为：

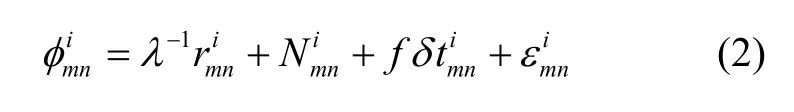
双差观测方程为：

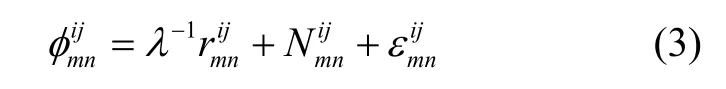
当存在转发式欺骗干扰时，如图1所示，转发器S在接收真实的北斗信号后，根据对目标的欺骗需求，在真实信号中加入一定量的延迟后进行转发。

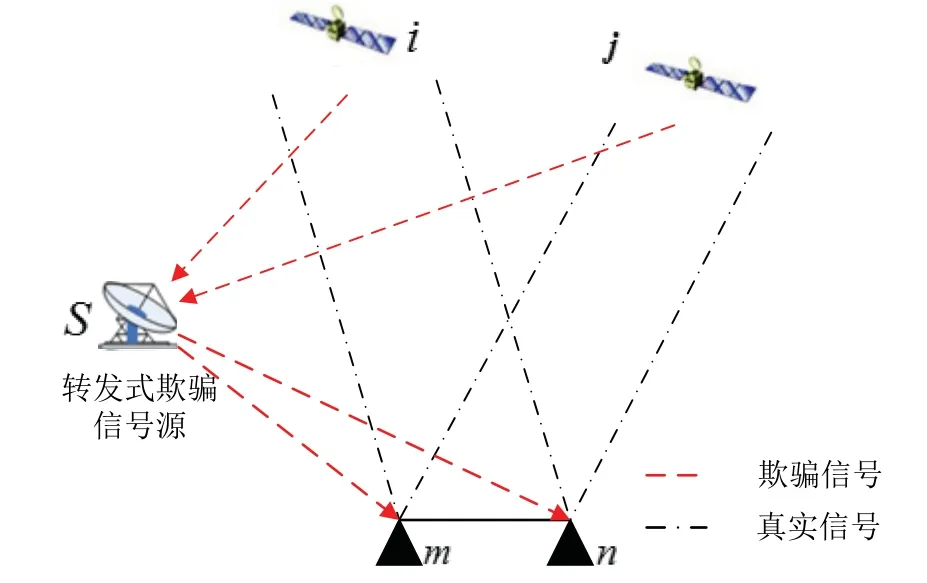
图1 转发式欺骗信号模型Fig.1 Repeated spoofing signal model

此时，欺骗信号的载波相位观测方程为：

式中：f表示载波信号频率，ts表示欺骗信号的延迟。

受欺骗干扰的影响，接收机m和n同时接收真实信号与转发器S播发的欺骗信号，会出现两种情况。1）接收机载波相位观测值φi和φj均为欺骗信号，则单差和双差观测方程为：

2）φi、φj分别为真实信号和欺骗信号的载波相位观测值，由式(2)和式(5)，则双差观测方程为：

从理论上分析，为转发器S载波相位观测值中包含的整周模糊度，当接收机m和n接收同一路欺骗信号时，相同，在不考虑观测噪声的情况下，的值为零；而受整周模糊度和星地间几何距离的影响，其值随时间变化一般不为零。两类信号的载波相位双差观测值存在明显的差异，为欺骗信号的检测提供了理论基础。

而在实际过程中，由于不同接收机对欺骗信号的捕获跟踪过程不能同步进行，式(6)中的与之间会存在一个整数差，致使的值非零，利用载波相位双差的方法难以直接检测出欺骗信号。并且式(7)表明，当接收机同时收到真实信号与欺骗信号时，除欺骗延迟外，一样会受到星地间几何距离以及整周模糊度的影响，增加了对欺骗信号的检测难度。

通过对比式(3)和式(6)可以发现，的值始终保持在一个固定的整数附近，不随时间的变化而变化；而由于受到星地间距离的影响，其值随卫星运动会发生不断变化。而可以视为在真实信号单差的基础上附加了一个固定值，在变化趋势上与有明显区别。因此，根据载波相位双差观测值的变化趋势能够区分三种情况下的差分信号，实现对欺骗信号的检测。

在检测出存在欺骗干扰的前提下，由卫星i和j得到一组载波相位双差观测值，在判断其所属信号类型的基础上，引入第三颗卫星r的观测值，将φr与φi、φj两两之间进行差分处理，根据φri与φrj的信号类型，可以进一步明确受到欺骗的卫星信号，从而避免欺骗信号对定位解算的影响。

2 基于PNN的欺骗信号检测模型

2.1 概率神经网络

概率神经网络是在径向基（Radial Basis Function，RBF）神经网络的基础上，结合Bayes决策准则和Parzen概率密度函数发展形成的一种前馈型神经网络，适应于解决模式分类和故障判断的问题，在对欺骗信号的检测方面具有优势。

Bayes决策准则是PNN分类判决的依据，设一组p维向量X= [x1x2…xp]，X属于不同类别ω1、ω2…ωm当中的一种，根据贝叶斯最小风险期望的原则，判断X∈ωm的条件为：

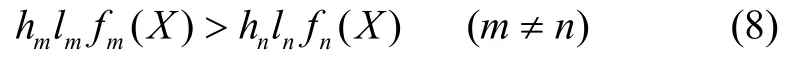
式中：hm和hn分别表示类别m和n发生的先验概率，lm和ln分别表示对类别m和n误判时对应的损失函数，fm(X)和fn(X)分别表示m和n的概率密度函数。

在对欺骗信号检测的模型中，先验概率h和损失函数l对所有类别都是相同的。因此，分类判断的关键在于确定概率密度函数f(X)。

PNN采用Parzen窗的非参数估计方法用于确定概率密度函数f(X)。

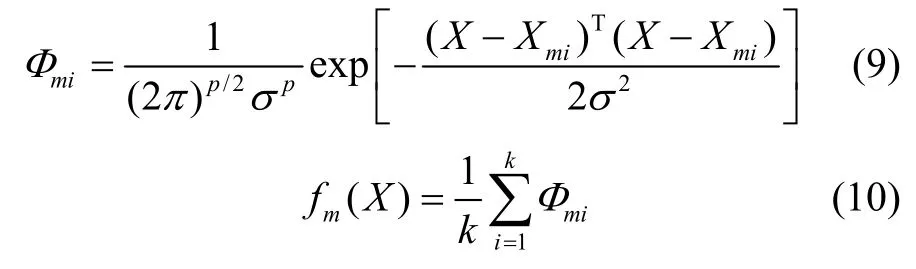
式中，k表示类别m中训练样本的总数，Xmi是类别m中第i个训练样本，σ表示平滑因子。

基于上述原理，概率神经网络模型由输入层、模式层、加法层和输出层四部分组成，结构如图2所示。

图2 PNN模型结构Fig.2 PNN model structure

在PNN结构中，输入层用来接收训练样本Xi，其神经元个数与样本中特征向量的维数一致；模式层分析特征向量与不同标签之间的对应关系，计算各个神经元的输出Φmi，其神经元个数等于样本总数；加法层将模式层中同一类别神经元输出的Φmi进行加权求和，计算fm(X)，得出样本数据与标签对应的概率密度函数，该层的神经元个数与样本种类相等；输出层则根据加法层的结果来确定样本类型与标签之间的概率关系，其中概率密度最大的神经元输出为1，其余为0，从而得出分类检测的结果。

2.2 欺骗信号检测流程

在载波相位双差检测技术的基础上，利用概率神经网络对转发式欺骗信号进行分类检测的流程设计如下：

（1）数据预处理

通过GNSS信号转发器搭建欺骗干扰环境，利用接收机获取不同场景下的北斗载波相位观测值数据，在对其进行双差处理后，得到载波相位双差观测值作为网络样本数据，并为不同类型的样本打上标签。

（2）概率神经网络训练

首先随机选取部分样本作为训练数据，对应PNN网络的输入层向量Xi；之后通过模式层神经元得出每一样本对应的概率密度函数，加法层神经元负责得出训练样本中同一类别双差信号对应的概率密度函数；最后由输出层神经元建立信号类型与样本标签之间的对应关系，并根据训练结果，不断调整平滑因子σ，优化网络性能。

（3）转发式欺骗信号检测

从样本数据中选取非训练部分作为网络测试数据，将测试样本输入训练完成的PNN网络，根据网络输出的分类结果，得出样本中双差观测值对应的信号类型，从而实现对欺骗信号的检测。

3 实验与分析

为了验证PNN对北斗欺骗信号分类检测的有效性，分别在楼顶和室内环境下进行了转发式欺骗检测实验，转发式欺骗平台设备由GNSS信号转发器、NovAtel发射天线和接收天线组成，数据采集平台由两个NovAtel-OEM628板卡、两个NovAtel702接收天线和软件接收机组成，实验设置如图3所示。

图3 实验设置Fig.3 Experimental setup

3.1 数据采集与处理

在楼顶实验中，GNSS信号转发器的接收天线与发射天线之间相距约20m，接收机的接收天线与转发器的发射天线之间相距约5m，两接收天线之间的距离为3m。实验包含两个部分：①接收设备正常开机，关闭GNSS信号转发器，此时采集的数据均为真实的卫星信号；②保持接收机正常工作状态，并开启GNSS信号转发器，此时采集的数据同时包含真实信号和欺骗信号。

在室内实验中，GNSS信号转发器的接收天线放置在楼顶，发射天线放置在室内，由于接收机在室内环境下无法接收到真实的卫星信号，确保采集的数据均为欺骗信号。

实验时间共计约120 min，采样频率为1 Hz，共采集到有效数据6735条。实验过程中的北斗可见星数以及卫星角度信息如图4所示。

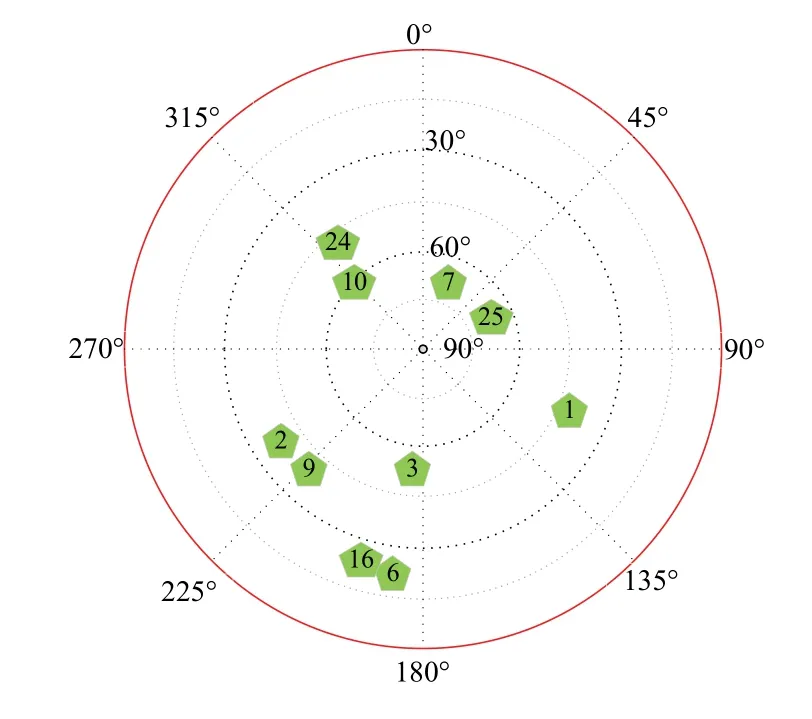
图4 北斗星空图Fig.4 BDS sky map

在得到载波相位观测值后，对采样数据进行差分处理，每一历元的10颗卫星信号可以获得45组双差观测值，不同信号类型的双差观测值如图5所示。

图5 载波相位双差观测值Fig.5 Carrier phase double difference observation

定义每100条数据为一组样本，共得到3015组样本数据，其中双差观测值的欺骗信号类别标签和样本容量如表1所示。

表1 样本数据设置Tab.1 Sample data settings

3.2 欺骗信号检测

根据PNN模式分类的方法，对欺骗信号的检测流程如图6所示。

图6 PNN检测流程Fig.6 PNN detection process

PNN模型采用MATLAB中现有的newpnn库函数构建，并在3015组数据中随机选择300组数据作为训练样本，100组数据作为测试样本。

在每组样本连续选取5个历元的数据输入PNN模型，通过多次的网络训练和样本回代验证，不断调整newpnn函数中的平滑因子参数σ，优化训练结果，得到最终的训练数据检测结果和检测误差如图7所示。

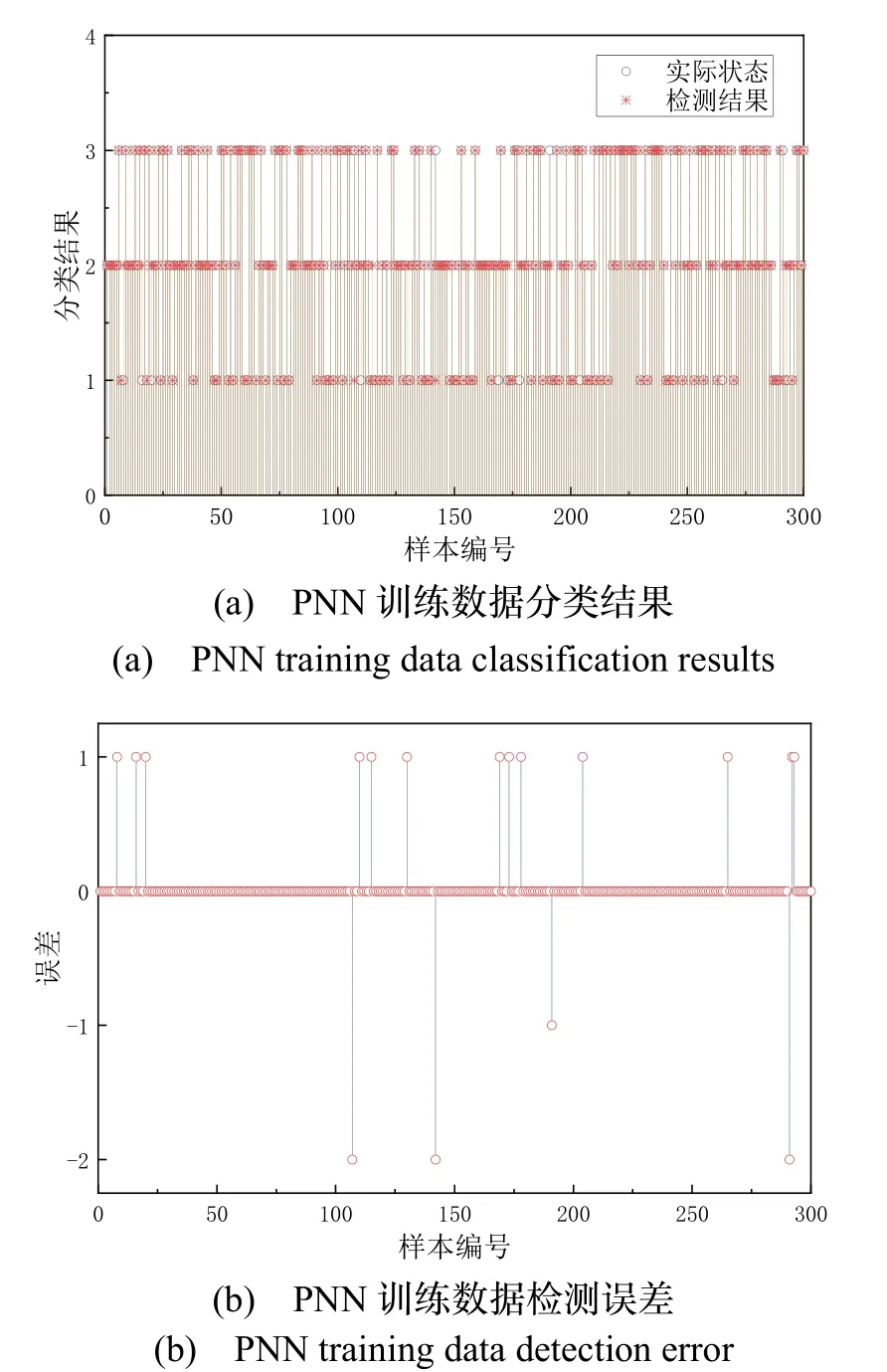
图7 PNN训练效果图Fig.7 PNN training effect diagram

图7表明，在300组训练数据中，PNN能够准确识别出283组数据的信号类别，检测准确率达到了94.33%；在对221组含有欺骗的数据检测中，仅有4组数据出现了误判，针对欺骗信号的检测成功率达到了98.19%。由此表明，PNN能够有效识别信号类别，检测出欺骗信号。接下来在3015组样本中随机选择100组作为测试数据，PNN检测结果和检测误差分别如图8所示。

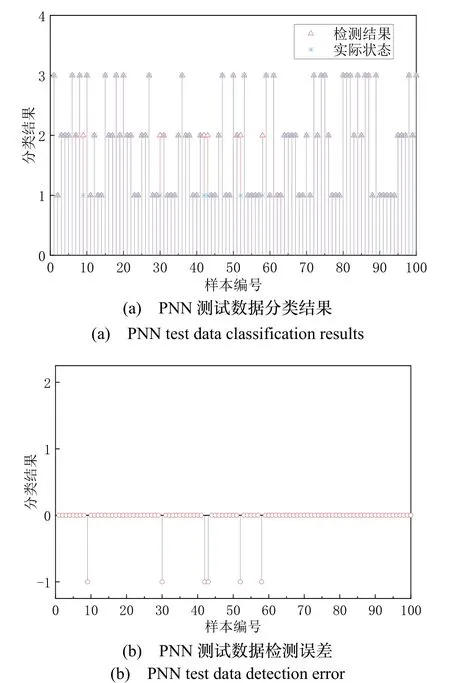
图8 PNN测试效果图Fig.8 PNN test effect diagram

图8表明，在仅有5个历元观测数据的情况下，经训练的PNN模型对欺骗信号的检测成功率能够达到94%。直接利用双差观测值检测的结果如图9所示，在45组数据中，双差观测值为0的有7组，直接检测的成功率仅为16%。

图9 双差法直接检测结果Fig.9 Double-difference method for direct detection results

为进一步验证样本中历元数和接收机基线长度对PNN检测结果的影响，分别选取不同的历元数和基线长度进行多次测试，检测结果和耗时如图10所示。

图10表明，PNN检测模型随样本历元数增加正确率逐步增大，样本历元数为100时准确率最高为98.51%，检测耗时不超过0.1 s，尤其在前10个历元之内的性能提升明显，在基线长度为3 m的条件下，检测正确率可以达到96.48%，耗时仅为0.062 s，能够满足对欺骗信号进行实时检测的要求；图10(a)进一步表明，当历元数较少时，检测正确率随基线长度增加有一定提高，当检测历元超出20之后，不同基线长度下的检测正确率基本保持一致，能够满足接收机在不同基线条件下对欺骗信号的检测需求。

在检测出欺骗干扰的前提下，根据PNN分类结果可以判断出受到欺骗的卫星信号。选取四组不同类别的载波相位观测值，用来模拟4颗卫星的信号，信号设置如表2所示。

表2 模拟欺骗信号设置Tab.2 Analog spoofing signal settings

将差分处理后的数据导入训练过的PNN模型，检测结果如表3所示。

表3 欺骗信号检测结果Tab.3 Spoofing signal detection result

根据表3中的检测结果可以判断，第一组数据中10号卫星的信号为欺骗信号，第二组数据中10号、24号卫星的信号为欺骗信号，进而在定位解算中剔除欺骗信号，保证定位结果的可靠性。

3 结 论

本文针对北斗转发式欺骗干扰问题，提出了一种基于PNN的欺骗信号检测方法。在构建概率神经网络的基础上，根据转发式欺骗干扰信号随时间变化的一致性，利用载波相位双差观测值对北斗欺骗信号进行分类检测，实测数据结果表明：（1）PNN模型能够准确识别不同差分信号的类型，有效检测出欺骗信号；（2）对欺骗信号的检测成功率可达98.51%，且耗时不超过0.1 s，能够满足实时检测的要求；（3）无需测量两天线之间的基线长度，适用于具有双天线或双接收机的单无人机以及多机协同情况下的北斗转发式欺骗干扰检测。