半球谐振子装配倾角误差对频率裂解的影响分析
2021-12-06宁友欢伊国兴奚伯齐解伟男魏振楠王常虹
宁友欢,伊国兴,奚伯齐,解伟男,魏振楠,王常虹
(哈尔滨工业大学航天学院,空间控制与惯性技术研究中心,哈尔滨 150080)
半球谐振陀螺是一种全固态振动陀螺仪,具有精度高、体积小、可靠性高、功耗低、启动时间短等特点。目前高精度的半球谐振陀螺具有0.0001 °/h的高精度,长达20年的使用寿命,可达0.995的高可靠性[1]。由于高精度、高可靠、结构简单,极具体积、质量等综合优势,在深空探测、卫星稳定控制、航天器导航、石油钻探、航海等领域具有广阔的应用前景[1-5]。
国内外针对半球谐振子频率裂解的形成演化机理以及调频和测试方法进行了大量的研究,但这些研究主要集中在谐振子加工误差及材料各向异性对频率裂解的影响方面[6-13],针对装配误差造成频率裂解的影响机理研究较少。霍炎等人针对质量分布不均匀对谐振子频率裂解以及质量缺陷对振动谐振子驻波漂移的影响进行了研究[7]。文献[8]推导了具有质量缺陷的半球形壳体的分频解析模型,并建立了一个预测不完美谐振腔微调质量的函数。在频率裂解修调方面,文献[9]研究了一种化学刻蚀方法来消除导致频率裂解的半球形谐振子质量不均匀性的第四次谐波,该方法可以将半球谐振子的频率裂解降低到0.05 Hz。胡晓东等人利用离子束去除半球形谐振器质量缺陷的第1-4次谐波,该方法能将半球谐振子的频率裂解从0.46 Hz减少到0.004 Hz[10,11]。针对频率裂解的测试,李绍良等提出了基于幅频响应特性的半球谐振子频率裂解与固有刚度轴方位角测定方法[12]。俄罗斯马特维耶夫提出了基于幅相频特性描绘法的固有刚度轴方位角和频率裂解的确定方法[13],为半球谐振陀螺仪的研究奠定了理论分析基础。装配过程中的装配误差产生应力、刚度分布不均匀,会对谐振子频率裂解、品质因数等性能产生影响,文献[14]针对装配误差对谐振子品质因数的影响进行了分析,并对减小装配误差的解决方案进行了研究。文献[15]针对非理想轴对称壳体谐振器的频率裂解的产生进行了分析,基于轴对称多曲面壳体结构的谐振器,提出了一种消除频率分裂的方法,并验证了所述方法的有效性。
本文针对半球谐振子振动性能受装配误差的影响展开研究,重点研究了装配过程中产生的倾斜误差对半球谐振子频率裂解的影响机理。首先基于半球谐振陀螺电容式驱动原理,将半球谐振子唇沿与平板电极等效为平板电容器,建立等效电容与装配误差之间的数学模型;然后根据等效电容两端电压与半球谐振子静电力之间的数学模型,分析静电力不均匀对谐振子刚度的影响;最后,建立刚度扰动对频率裂解的影响机理模型,分析倾角误差对谐振子频率裂解的影响演化机理。
1 装配误差对频率裂解形成机理分析
1.1 半球谐振子频率裂解形成理论分析
半球谐振子的固有频率不仅受材料性能的影响,而且与其几何参数有关,完美的谐振子不会产生频率裂解。然而,材料的各向异性和谐振子制造工艺等误差的四次谐波会导致谐振子中出现两个相互成45 °夹角的固有刚性轴。
如图1所示为半球谐振子二阶振动等效模型,黑色的圆为谐振子环形模型的外边缘,红色和蓝色分别是两个振动模态的振动图,两个模态形成互相间隔45 °的两个固有轴。半球谐振子在振动时,沿这两个轴中每一个轴的振动固有频率都能达到极大值和极小值,为了便于描述,一般将固有频率较小的轴称为“重轴”,固有频率较大的称为“轻轴”。振动圆频率的极大值和极小值的频率差称为固有频率的裂解,频率裂解定义为:
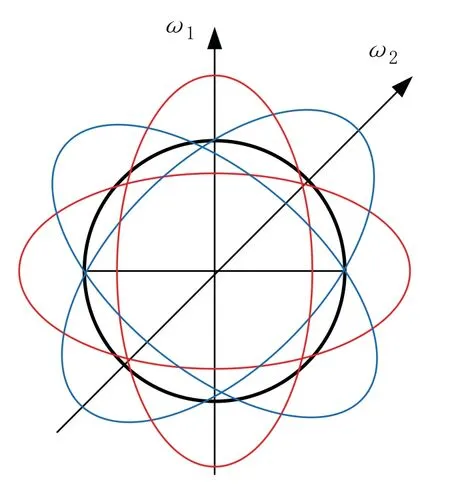
图1 谐振子二阶振动等效模型Fig.1 Second-order vibration equivalent model of resonator

对具有频率裂解的谐振子振动信号进行采集,谐振子振动信号的幅频响应分析曲线如图2所示。
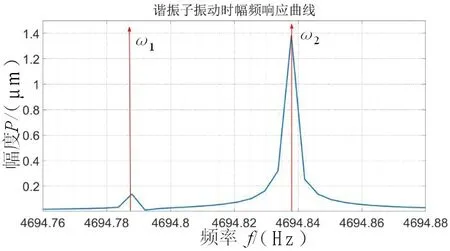
图2 半球谐振子频率裂解信号Fig.2 Hemispherical resonator frequency split signal
当所受激振力的方位角与固有刚性轴不重合时,半球谐振子两个刚性轴处的振动模态会被不同程度激励起。振动信号出现了两个信号峰值,分别对应谐振子刚性轴的两个振动模态,信号峰对应的频率即为振型的谐振频率,两个峰的不同幅值反映了激振力方位与固有刚性轴方位的偏差。
由于材料缺陷及加工误差导致两个节点和两个波腹组成的两种工作模式之间出现频率差。这种缺陷导致陀螺效应的损失,甚至不能检测角运动。因此,频率裂解的存在不仅能引起驻波漂移,产生机械耦合误差,还会降低半球谐振陀螺的灵敏度。频率裂解是造成半球谐振陀螺零偏误差的主要原因之一,频率裂解的形成机理研究是提高半球谐振陀螺仪测量精度的关键技术。
1.2 半球谐振子装配倾角误差与等效电容的模型
半球谐振子与平板电极基座的装配通常采用粘合剂将二者固连,在表头装配过程中,由于设备、夹具等方面的原因,导致谐振子在装配过程中产生了偏心、倾斜等装配误差,直接影响谐振子与平板电极初始的间距不均匀,从而导致谐振子的振动在正交轴分解时产生误差。同时,装配误差也会影响静电力的分布,改变了刚度分布的均匀性。半球谐振子装配倾角误差如图3和图4所示。
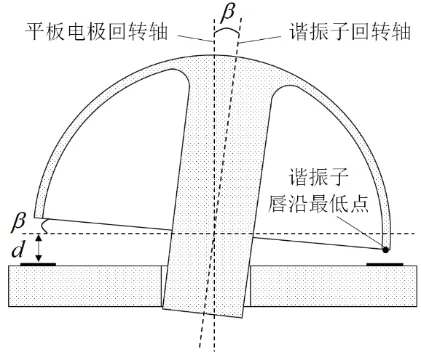
图3 安装倾角误差示意图Fig.3 Schematic diagram of installation inclination error
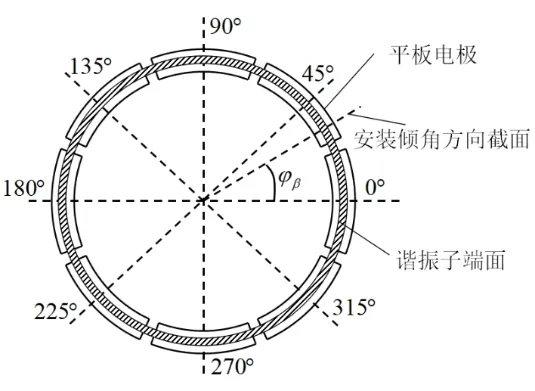
图4 安装倾斜方位角示意图Fig.4 Schematic diagram of installation tilt azimuth
由于装配倾角误差的存在,装配后半球谐振子振动受静电力的影响,导致刚度分布不均匀,从而对谐振子频率裂解产生影响。半球谐振子唇沿与平板电极形成等效电容,电容值由谐振子唇沿与平板电极的正对投影面积以及两者之间的距离决定。由于受到装配工艺的限制,谐振子与电极基座装配过程中,谐振子回转轴与平板电极回转轴将不可避免的产生大小为β的安装倾角,由此造成谐振子唇沿与平板电极间周向各点的间隙不同。假设其平均间距为d,其中间距最小处对应谐振子唇沿最低点,如图3所示。连接谐振子回转中心与谐振子唇沿最低点所得直线在平板电极表面的投影与0 °电极轴线方向存在角βφ,称为安装倾斜方位角,如图4所示。若沿着图4中通过回转轴与0 °电极轴线的切割平面将谐振子及平板电极向周向方向展开,则可得到如图5所示谐振子周向展开图。

图5 谐振子周向展开图Fig.5 Circumferential development diagram of harmonic oscillator
由图5分析可知,各激励及检测电容间距在安装倾角及倾斜方位角的作用下呈正弦规律变化,通过对该规律的解析,可以根据测量得到的各静态电容值获取安装倾角和安装倾角方位。
如图6所示的平板电极及其等效示意图,电极均匀分布在基板表面,在空间中处于同一平面,各电极周向边界通常设计为互相平行。基于此,为了便于分析,引入“等效间距角”的概念对各电容的分布进行建模[5]。根据对检测电容几何结构的分析可得到等效电容的周向边界,其径向边界则由谐振子内表面半径1r及谐振子外表面半径2r决定。
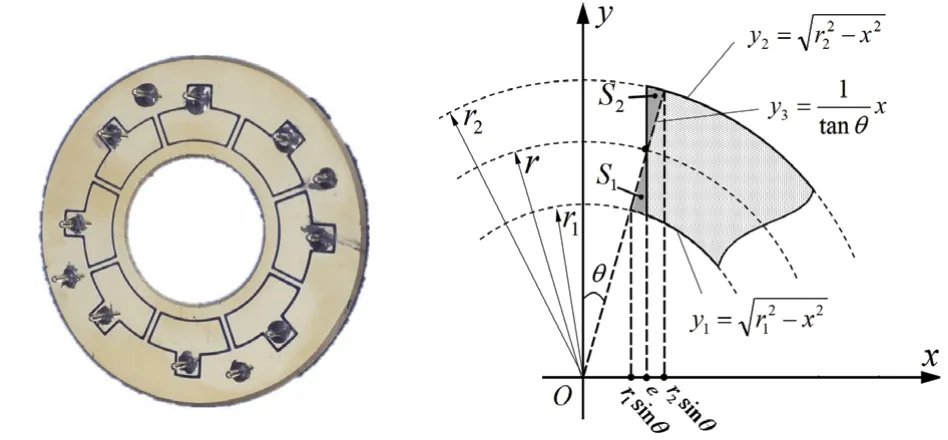
图6 平板电极及其等效示意图Fig.6 Schematic diagram of plate electrode and its equivalent
图6中实线包围区域为实际的激励或检测电容区域,各电极间由宽为2e的电气间隙隔离。为便于电容积分计算,假设各电极由中心角为2θ的扇形区域分割,称其为等效间距角。当图6中阴影区域S1与S2面积相同时,利用电气间隙隔离2e及等效间距角2θ计算得到的电容值相同。θ可由式(2)计算得到。
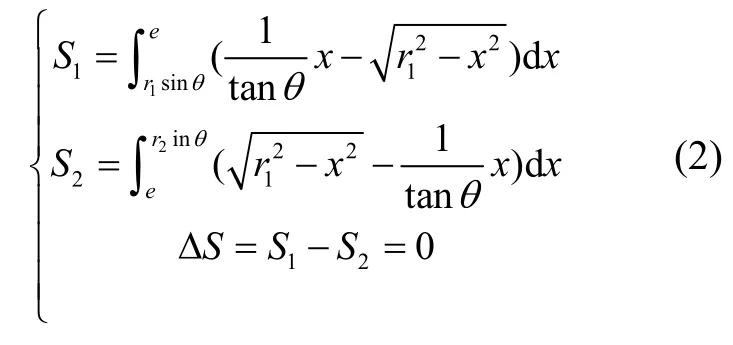
电极的边界可利用周向方向的角度表示:
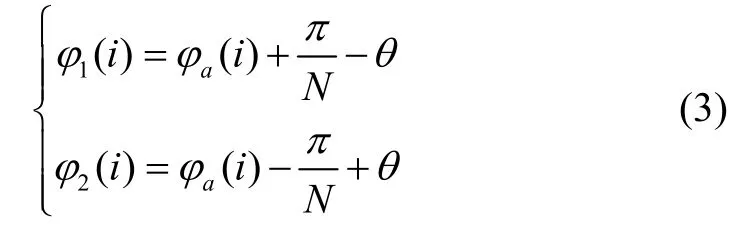
式(3)中,φ1(i)、φ2(i)为第i个电极的周向边界;φa(i)为第i个电极的轴线角度,如对于第一个电极(0°电极)有φa(1) = 0°;N=8为电极的数量。
当半球谐振子振动时,唇沿表面与平板电极之间的间隙可以表示为:
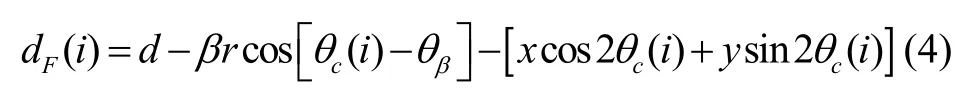
则根据平行板电容器原理,忽略谐振子端面的扭转形变,可得第i个电极的静态容值[5]CF(i):
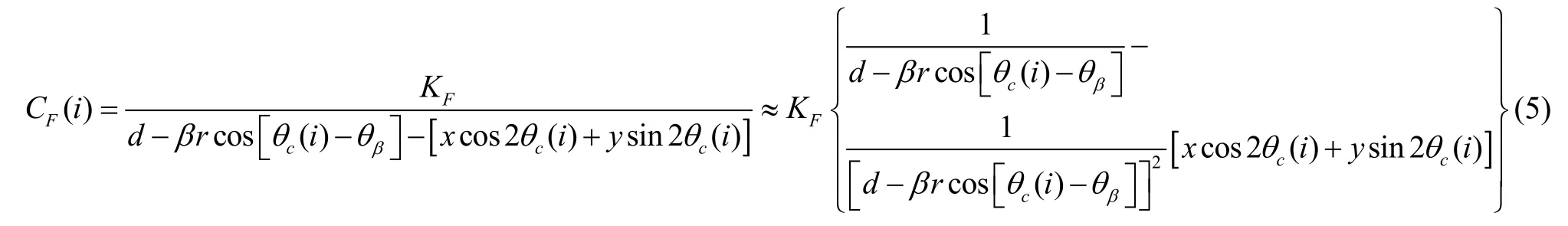

其中:k为静电常数,k= 9.0×1 09N· m2/C2;β为以 0 °电极轴线为起始位置的圆周角;△θF=θi(r) -θi(l)表示平板电极上第i个电极所占位置角度。
1.3 半球谐振子激励模型
半球谐振陀螺采用电容式驱动,半球谐振子唇沿与平板电极之间形成等效平板电容器。因此,根据拉格朗日力学原理,谐振子唇沿与平板电极之间的静电力为:

其中,Ec为存储的电势能,
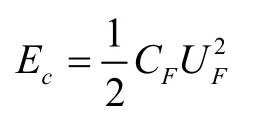
UF为在电容两端施加的电压。
对于第i个电容器,当谐振子振动时,对静电力进行简化后其表达式为:

由于倾斜导致的误差可以表示为:
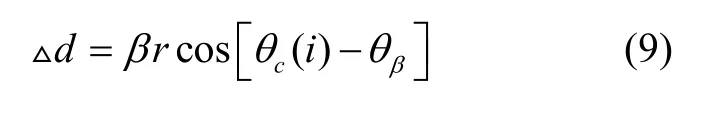
则静电驱动力可以表示为:

在实际装配过程中,装配误差可以控制到很小的范围,即:d≫Δd,对静电力进行泰勒局部展开,忽略高次项,保留低次项后可得:

分析式(11)可知,静电驱动力的第二项与倾斜误差有关,由于该力的存在会影响谐振子的刚度系数,倾斜误差的存在导致的刚度变化表示为:
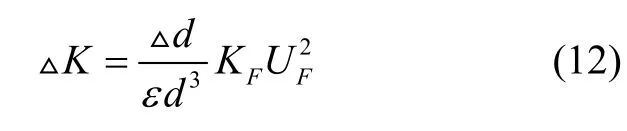
在刚度扰动的情况下谐振子频率裂解可写为:
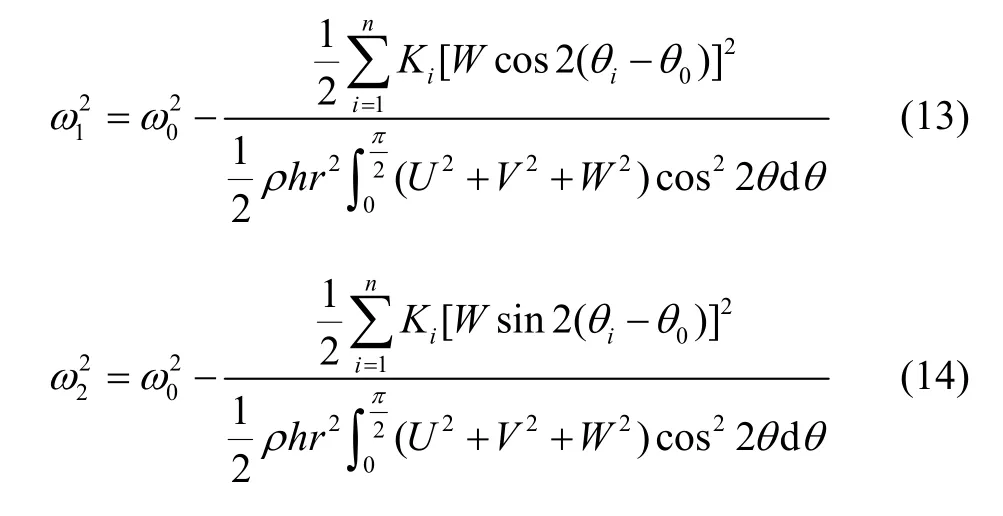
其中Ki表示离散后分析的第i个不平衡刚度大小,θi表示不平衡刚度的方位。
将式(13)(14)带入式(1)中,化简后即可确定装配倾角误差对半球谐振子频率裂解影响的数学模型。
2 仿真及结果分析
基于等效电容与装配误差之间的数学模型,选取0 °位置的电极为参考,通过数值仿真分析软件对不同安装误差状况下静态电容值的变化规律进行仿真,仿真参数如表1所示,仿真结果如图8所示。

表1 模型仿真参数Tab.1 Type simulation parameters

图8 电容安装误差静态模型Fig.8 Static model of capacitor installation error
由图8的仿真结果分析可知:随着安装倾角的增加,电容容值偏离平均值的程度也逐渐增大,而在同一倾角大小下,电容值偏离平均值的程度由倾角相位决定。电容容值的变化由倾角大小的增加和倾角相位共同确定,即装配倾角误差可以由电容值的变化唯一确定。
基于等效电容模型,等效电容值由谐振子唇沿与平板电极的正对投影面积以及两者之间的距离决定。通过电容的微小变化,等效半球谐振子的振动。由于倾角误差导致等效电容的变化而形成的静电力分布不均匀造成刚度扰动的数学模型,如式(11)所示,取理想条件下半球谐振子受到静电力激励时的刚度为参考,假设参考值为0,由倾角误差引起的谐振子刚度扰动偏离平均值的误差仿真结果如图9所示。

图9 刚度随方位角变化关系Fig.9 The relationship between stiffness and azimuth
由图9分析可知,谐振子与电极基座装配过程中产生的倾角误差导致等效电容两端的静电力在安装倾角及倾角方位角的作用下呈正弦规律变化。即安装过程中形成的倾角误差将会影响每一个电容的变化,进而在周向各点上产生了静电力分布不均匀,其中间距最小处的静电力较大,对刚度的影响也较大。刚度扰动引起频率裂解的数学模型如式(12)-(14)所示,为进一步分析量化其影响规律,采用数值仿真分析软件对该数学模型进行仿真分析,分析结果如图10所示。

图10 刚度变化与频率裂解的关系Fig 10 The relationship between stiffness change and frequency cracking
由图10的仿真结果分析可知,频率裂解与刚度不均匀变化量呈正比关系。以直径为30 mm的石英半球谐振子为例,当其刚度变化0.05%时,刚度缺陷所引起的频率裂解约为1 Hz。
基于上述的分析,当石英半球谐振子与基座的装配倾角误差为1角秒时,频率裂解为10-6Hz量级,而当装配误差增大到60角秒时,频率裂解将达到10-4Hz量级。因此,根据半球谐振子应用需求,实际装配过程中,为将装配误差造成的频率裂解控制在10-4Hz量级以下,装配倾角误差应控制在1角分范围以内。
3 结 论
本文围绕半球谐振子装配过程中产生的偏心、倾斜等误差对频率裂解的影响展开研究,建立装配误差对频率裂解的影响机理模型,首先分析了倾角误差对半球谐振子静电力分布不均匀的影响,建立由于刚度扰动导致频率裂解的数学模型,给出了安装倾角误差对频率裂解的演化机理。以30 mm熔融石英半球谐振子为例进行误差机理模型的仿真验证,结果表明,谐振子与基座的装配倾角误差为1'时,由安装倾角误差引入的频率裂解为10-4Hz量级。装配误差不仅会影响频率裂解,也会影响谐振子品质因数、阻尼分布均匀性等性能指标,从而导致驻波漂移,影响半球谐振陀螺的精度。因此,对装配误差进行深入细致的研究,对优化装配工艺,提高半球谐振陀螺仪性能有着重要的意义。
