基于改进的层次分析法和模糊综合评价法的灌区农业水权分配

高娟娟，贺华翔，赵嵩林，谢纪强

（1.中国水利水电科学研究院，北京100038；2.河南省安阳水文水资源勘测局，河南安阳455000）

0 引言

在中国，农业不仅是国家稳定的基础，也是经济社会发展的前提。然而，由于农业灌溉节水技术相对落后和水利配套设施覆盖率低，导致典型的农业用水效率低的问题。且不断增长的生态、生活、工业用水挤占农业用水，用水需求与可利用水资源量严重不匹配。因此，开展有关灌区农业水权分配、灌区水资源管理的研究以缓解当前灌区的缺水问题就显得尤为重要。灌区农业水权分配是完善农业水权制度、夯实农业水价改革和建立水权市场的重要基础。通过适当引水和配水以及改进田间灌溉设施，实现水资源的有效利用、促进农业发展、保障粮食安全。

在过去的30年中，国内外专家学者对初始水权分配问题进行了大量的研究。早期的研究包括John[1]和Zhong Jing W[2]从公平性和可持续性视角分配初始水权。根据土地面积、资金投入、公法、用水优先序、用水许可和合理收取水费分配初始水权[3-6]，弥补了原有灌区管理和取水许可制度的不足。随着研究的深入，还开展了一些有关初始水权分配技术的研究，Zhang L N[7]在考虑条件风险值理论和基尼系数约束的基础上，建立了水权分配的两阶段随机规划模型，通过优化水权分配方案，降低了局部水资源短缺的不公平风险。Wang H L[8]运用层次分析法建立行业水权分配的层次结构模型，并对行业水权分配进行了研究。胡洁[9]利用多层次多目标模糊优选方法对流域初始水权进行分配，分配结果较其他分配模式更具公平性、高效性及合理性。孙建光和顾沁扬等[10,11]对农业水权分配方法和分配制度进行了研究，为缓解农业用水矛盾提供了有效方案。管新建[12]应用基尼系数法分配灌区农户间水权，为灌区水权分配提供了新思路。姚明磊和董斌[13]针对不同用水部门间日益激烈的用水矛盾，建立多目标规划模型，将县域水权合理分配至各用水部门。刘子豪等[14]通过驱动力-状态-响应(DSR)框架对46 分水权制度进行分析，认为农业水权制度的完善和政策响应相互影响。

然而，以上初始水权分配方法各有利弊。非技术类方法因面积、土地、政策等因素的变化实时性较差；技术类方法包括最初的层次分析法、遗传算法和两阶段随机规划等方法基本能够解决多目标多层次的水权分配问题。但是，随着相关研究的深入，该类方法的不足在于水权分配过程中受主观性影响较大导致结果差异大。且鲜有将此类方法应用于灌区农业水权分配研究中，本文以灌区各支渠间水权分配为研究对象，采用改进的层次分析法和模糊综合评价法作为技术支撑，通过构建灌区农业水权分配层次结构图，对每一层指标进行标度赋值，确定评价指标优先序等级，引入模糊综合评价法，建立模糊综合矩阵，进行一致性检验，最终得到灌区各支渠间农业水权分配结果。提出一种在灌区现状约束条件下使经济效益达到最优的灌区各支渠间水权分配方法。

1 基于改进的层次分析法的灌区农业水权分配模型的构建

20世纪70年代，层次分析法（AHP）的概念最初被T L Saaty[15,16]提出，AHP的最大优点在于它能够处理复杂的实际问题，并且易于操作。经过不断改进[17,18]，已有研究表明，因层次分析法具有独特性和优越性而被广泛应用于地理信息系统[19,20]、生态脆弱性评价[21]、灌溉水质指标评价和灌溉工程应用[22,23]、灌区农业用水管理评价[24]等领域。层次分析法也被广泛应用于解决水权分配中多层次、多目标的复杂问题[25]。然而，针对已有层次分析法解决初始水权分配过程中存在的欠缺与局限性，仍有很大的改进空间。本文针对灌区现状水权分配模式未能综合考虑各支渠基础条件、经济效益和生态环境等因素，提出采用改进的层次分析法和模糊综合评价法解决灌区内工程、社会、经济和生态准则中定性指标的模糊性。一般情况下斗农毛地理位置相距较近，基础条件等亦相差不大，对其进行农业水权分配意义不大，故本文仅对和平灌区支渠间农业水权进行分配，在灌区现状约束条件下探寻经济效益最优的分配方法。

1.1 构建灌区农业水权分配层次结构图

德尔菲法是在20世纪50年代发展起来的一种广泛用于帮助预测各种学科决策的方法。本研究采用德尔菲法（Delphi method）[26]结合专家经验对调查结果进行分析，构建一套结构强、代表性高、实用性强的灌区农业水权分配体系，由目标层、准则层、评判层和指标层组成的灌区农业水权分配层次结构图，见图1。层次划分为4 类二级指标、12 类三级指标和17类四级指标。

1.2 改进的层次分析法

1.2.1 标度的转换

原层次分析法构造判断矩阵过程中以“1-9”的标度赋值较粗糙，有可能出现与实际情况相反的逆序，且矩阵一致性与思维一致性相脱节，不能准确量化每一层不同指标的隶属度关系。经过大量研究理论知识及实践经验认为采取指数标度进行分析精度较高。一，指数标度以心理学中的韦伯-费希纳定律[16]为基础，使判断思维与客观判断具有高度一致性；二，指数标度排序权值较为精细，缩小了人们的判断差值；三，指数标度允许有多种形式。因此，指数标度具有的优异性能可以克服“1-9”标度存在的问题。标度之间的转化，见表1。

1.2.2 判断矩阵的建立及一致性检验

（1）判断矩阵的建立。对每一层指标进行两两比较，根据两个指标相对重要性进行标度赋值，并进行标度转换得到eij值(表1)。构建判断矩阵E=(eij)n×n。

表1 指标标度转换Tab.1 Evaluation index scale conversion

计算判断矩阵的特征向量[28]。公式如下：

式中：Gi为判断矩阵E的每一行元素的乘积，i=1，2，3，…，n；Pi为Gi的k次方根值，k为判断矩阵E的阶数；Wi为判断矩阵E的特征向量。

计算判断矩阵E的最大特征值，计算公式如下：

式中：(EW)i为判断矩阵E=(eij)n×n与特征向量Wi的乘积；λmax为判断矩阵E的最大特征值。

（2）判断矩阵的一致性检验。本研究通过建立模糊一致性矩阵对判断矩阵进行深入检验。对判断矩阵E=(eij)n×n的每一行进行求和，记为（其中i=1，2，…，n），uij=得到与判断矩阵E相应的模糊一致性矩阵U=(uij)n×n。对于矩阵E和矩阵U，有如下两个检验指标：

当α<0.2，且β<0.1 时，认为模糊互补矩阵较为符合现实，可继续进行下一步计算；当α>0.2，或β>0.1 时，认为模糊互补矩阵不符合实际，需要专家进行重新判断打分，并按步骤重新计算，直至符合条件为止。

1.3 灌区农业水权分配相关权重系数确定

(1)在确定准则层、评判层、指标层中各元素相对权重及优先序等级后，对指标层中各个指标的综合权重系数进行计算：

式中：Fh为指标层中，第h个评价指标的综合权重系数(h=1，2，…，17)；Bp为准则层中，第p类准则的权重系数(p=1，2，3，4)；Cq为评判层中，第q个评判指标的权重系数(q=1，2，3，…，12)；Dh为指标层中，第h个评价指标相对权重系数。

(2)对灌区中各支渠赋予0～1 之间的数值进行隶属度分级，根据各支渠所属隶属度等级，结合指标层中各评价指标综合权重系数，最终得灌区内各支渠农业水权分配总权重系数。计算公式如下：

式中：Ql为灌区中第l条支渠的总权重系数(l=1，2，…，16)；gl为第l条支渠的隶属度。

2 模糊综合评价法

本研究采用模糊综合评价法将灌区农业水权分配过程中不可定量描述的指标进行定量处理。对复杂系统进行优选，对隶属度函数进行模糊化处理，以解决评价等级在区间端点处数值小幅度变化时产生的跳级问题。计算得隶属度矩阵R和模糊综合矩阵B。令为第t个等级的隶属度（等级划分见表3），rh为评价指标的实际值，为第t个评价等级的上限，为第t个评价等级的下限，为第t个评价等级的均值。

(1)对于越大越好指标。

其他等级隶属度为0；

其他等级隶属度为0；

其他等级隶属度为0；

(2)对于越小越好指标

其他等级隶属度为0；

其他等级隶属度为0；

其他等级隶属度为0；

根据以上公式（10）～（19）计算得到每一层指标的隶属度矩阵R，

结合改进的层次分析法和模糊综合评价法将每一层指标的权重矩阵进行模糊变换，可得模糊综合矩阵B。

式中：W为与公式（5）中特征向量Wi对应的矩阵。

3 实例研究

3.1 研究区概况

和平灌区位于庆安县中部，呼兰河左岸的干支流河漫滩及一级阶地上。灌区内共有25个行政村，283个自然屯，总人口5.6 万人。灌区内共有3 座渠首，干渠1 条，长45 km，支渠16 条和11 条直属斗渠及3 处扬水站支渠，总长61.33 km，排水干渠15 条，总长51.2 km。灌区工程配套后，采用节水灌溉方法和节水工程技术，渠系水有效利用系数由改造前的0.5 提高到0.62。

3.2 和平灌区可分配水权总量

按照县域内农业可分配水量核定情况，2016年和平灌区实灌面积6 666.67 hm2，有效灌溉面积4 866.67 hm2，分配水量为4 754.12 万m3，供水水源为地表水，见表2。本次按实灌面积进行分配。

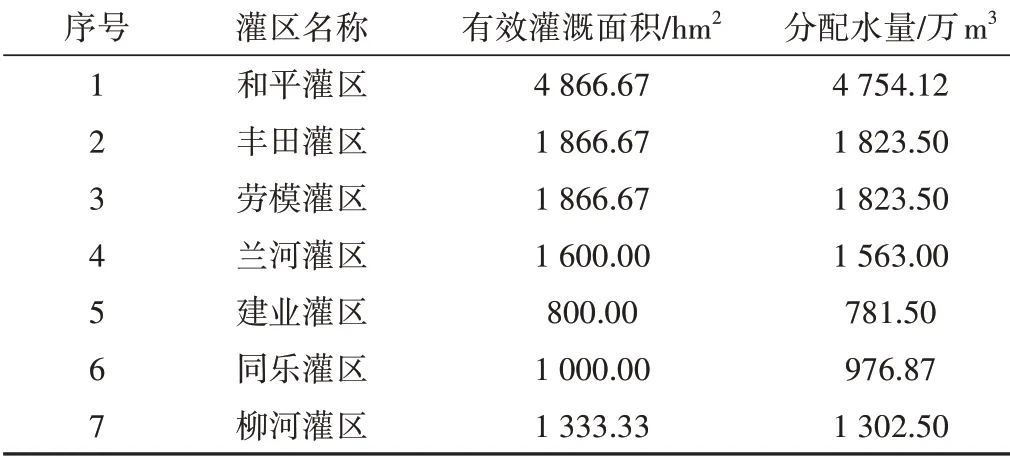
表2 2016年庆安县和平灌区用水量分配方案Tab.2 Water allocation scheme of irrigation district in qing’an county

3.3 建立灌区农业水权分配指标体系

各层指标的选取应综合考虑其代表性、独立性、关联性、易于量化、简单、直观和实用性等特点。并结合研究灌区经济、社会、环境和自然状况，选取的指标包含4 个2 级指标、12个3级指标和17个4级指标。具体见图1。

3.4 评价指标优先序等级

评价指标优先序等级即对指标层中评价指标进行优先程度排序。综合考虑和平灌区现状条件和各评价指标实际取值，结合评价指标相对重要程度，对指标层各评价指标隶属度分级标准进行范围评定，见表3。

表3 评价指标隶属度分级标准Tab.3 The classification standard of membership degree of evaluation index

3.5 模糊综合矩阵的建立和一致性检验

根据和平灌区农业水权分配基础条件，对每一层指标进行标度赋值，引入模糊综合评价法，建立模糊综合矩阵。并利用文中1.2.2节中的公式(6)、(7)计算α、β值，检验模糊综合矩阵的一致性，经验证均满足要求，见表4～表11。

表4 准则层模糊综合矩阵Tab.4 The fuzzy judgment matrix of criterion layers

表5 评判层评判指标C1～C6模糊综合矩阵Tab.5 The fuzzy comprehensive matrix of judging indicators C1～C6

表6 评判层评判指标C7～C8模糊综合矩阵Tab.6 The fuzzy comprehensive matrix of judging indicators C7～C8

表7 评判层评判指标C9～C11模糊综合矩阵Tab.7 The fuzzy comprehensive matrix of judging indicators C9～C11

表8 指标层评价指标D2～D3模糊综合矩阵Tab.8 The fuzzy comprehensive matrix of evaluation index D2～D3

表9 指标层评价指标D7～D8模糊综合矩阵Tab.9 The fuzzy comprehensive matrix of evaluation index D7～D8

表10 指标层评价指标D9～D10模糊综合矩阵Tab.10 The fuzzy comprehensive matrix of evaluation index D9～D10

表11 指标层评价指标D15～D17模糊综合矩阵Tab.11 The fuzzy comprehensive matrix of evaluation index D15～D17

3.6 灌区农业水权分配结果

通过以上计算方法，计算得和平灌区16 条支渠水量分配结果见表12和图2所示。

表12 和平灌区支渠农业水权分配结果Tab.12 The results of water rights allocation among the branch canals of Heping irrigation district

根据表12 和图2 中灌区农业水权分配结果，1 支渠、3 支渠、5 支渠、6 支渠、7 支渠、8 支渠、9 支渠、12 支渠、15 支渠、16 支渠模型分配水量均大于现状按面积分配水量，变幅范围在-0.09%～-9.90%，2 支渠、4 支渠、10 支渠、11 支渠、13 支渠、14 支渠模型分配水量均小于现状按面积分配水量，变幅范围在0.97%～8.62%。根据大量研究表明：水分生产函数因不同作物、不同生育期、不同地区、不同基础条件而有显著差异[29-31]。因此，和平灌区不同支渠水分生产函数各不相同，通过模型分配结果能够实现产量最大化，使水分生产函数计算值高的农田最大程度提高产量，水分生产函数计算值低的地块几乎不减产，最终达到经济效益最大化，为区域经济发展提供新思路。

4 结论与建议

本文通过改进的层次分析法结合模糊综合评价法构建的研究灌区农业水权分配模型，得到各支渠水权分配结果。所得结果由不同支渠计量设施配备情况、渠道设施建设情况、节水控灌技术应用、粮食产量、水资源有效利用率、人口因素、灌溉面积、可交易水资源率、经济效益、收缴水费情况、生态环境等因素综合影响下决定的，是各层次各种影响因素综合作用的结果。与现有分配方式即仅根据各支渠面积分配得到的水量结果有一定的偏差，范围在-9.90%～8.62%。

综上所述，水利设施配备完善、经济效益显著的支渠分配水权大一些，水资源利用率明显偏低、经济效益低的支渠分配水权少一些，本文基于分配模型所得结果以经济效益最大为总目标，带动当地农业发展，有利于地区经济长足发展。

（1）在保证公平性及效率性的基础上，对于灌区各支渠间最终水量分配比例，应综合考虑优化模型下支渠间水权分配和现状水资源量分配情况，通过进行公众参与、民主协商等方式确定。

（2）本次在对和平灌区进行水权分配过程中，强化经济效益，公平性指标弱化一些，希望未来能健全相关政策，充分体现土地分配中的公平性，给农户平均分配基础条件良好、经济效益高的地块和基础条件差、经济效益低的地块，以此实现经济效益最优。

本文所得结果可以给决策者提供技术支持，但在应用于灌区支渠间水权分配时还应与灌区实际情况相结合。