基于无监督迁移学习的电梯制动器剩余寿命预测

姜宇迪，胡 晖，殷跃红

(上海交通大学 机械与动力工程学院，上海 200240)

电梯制动器是电梯的重要安全装置，其性能衰减将直接影响电梯的运行安全[1-4].目前，电梯制动器寿命预测多采用传统的机器学习法[4-5]，即根据全生命周期的标注数据学习回归算法并进行预测分析[6-7].然而，电梯制动器作为高可靠性设备，其衰退周期长，全生命周期下的大量标注数据不易被采集，从而严重限制了传统机器学习方法的寿命预测效果.因此，需要探索能够得到大量电梯制动器衰退数据并进行剩余生命周期(RUL)精确预测的新方法.利用实验室样机仿真加速电梯制动器衰变的方法可以采集到大量标注数据，但所得仿真数据与在真实工作环境中得到的数据存在明显分布差异，会影响预测算法的结果.因此，如何迁移运用不同类型的大数据是算法研究的关键.

迁移学习[8]是一种机器学习新方法，其将仿真数据集定义为源领域，将真实工作环境中的数据集定义为目标领域[8-9]，以减少分布差异对预测结果的影响，从而提高算法的精度[10-13].在工业设备的应用方面，基于迁移学习的寿命预测和故障诊断算法尚不成熟.Sun等[14]利用稀疏自编码和Kullback-Leibler (KL)散度实现了对机器工具的寿命预测.Jia 等[15]利用基于域自适应的深度卷积神经网络实现了在不同噪声环境下轴承的故障诊断.Zhang等[16]提出通过快速傅里叶变换的方法将频谱数据映射到子空间，并利用子空间对齐的方式实现不同工况下轴承的故障分析.以上方法利用迁移学习将源领域与目标领域的数据在特征空间进行对齐，可以实现不同工况下设备的高精度RUL预测.但以上算法针对不同型号设备的预测效果却不佳，且其中的特征提取器并未考虑传感器数据在时间序列上产生的异常情况.此外，在训练过程中，将特征提取器和回归网络联合训练导致了对同一型号设备的过拟合，从而直接影响最终预测结果.

针对上述问题，提出一种基于映射的无监督深度迁移学习(UDTL)法，利用仿真制动器的训练网络判定实际制动器的健康状态，从而对真实工作环境中电梯制动器的RUL进行精准预测.该方法借助长短期记忆网络自编码器(LSTM-ED)实现对原始数据的特征提取.其根据健康数据训练模型，将网络重构序列与原始序列的差方序列作为特征序列，因此特征领域实际是传感器数据在时间序列上异常值的数据表征，从而保证了不同设备在特征领域中均具有一定的相似性；结合最大平均差异实现仿真数据与实际制动器数据在特征领域的再次对齐，从而保证两者在特征序列上的一致性，提高预测精度.同时，用分步训练法代替传统的联合训练法.在预测过程中，提出在线微调的方法，利用得到的新数据逐步更新特征提取器，从而实现对新设备的高精度寿命预测.

1 制动器失效成因分析

在电梯运行过程中，制动器的主要制动工作模式如下：当电梯轿厢到达需停站时，曳引机根据设定好的程序减速至极低的转速，同时电磁线圈断电.在弹簧压力作用下，闸瓦再次抱紧制动轮，并利用摩擦片的摩擦力制停曳引机.

根据电梯的工作模式进行制动器失效分析(见图1).可知，电梯在运行过程中出现制动衰退的原因主要为制动力矩过小、制动器气隙和制动距离过大以及摩擦片磨损.在设计过程中，本文选用的电梯制动器符合设计指标，即初始条件下制动器气隙、制动距离、摩擦噪声和制动力均为正常值.但在长期运行过程中，制动瓦片磨损会增大制动器气隙，摩擦噪声会随摩擦系数减小而增大，制动力减小，制动距离随之增大.根据具体失效原因，将制动器间隙、编码器读数、摩擦噪声和制动加速度作为原始数据，进行制动器寿命预测算法分析与试验.

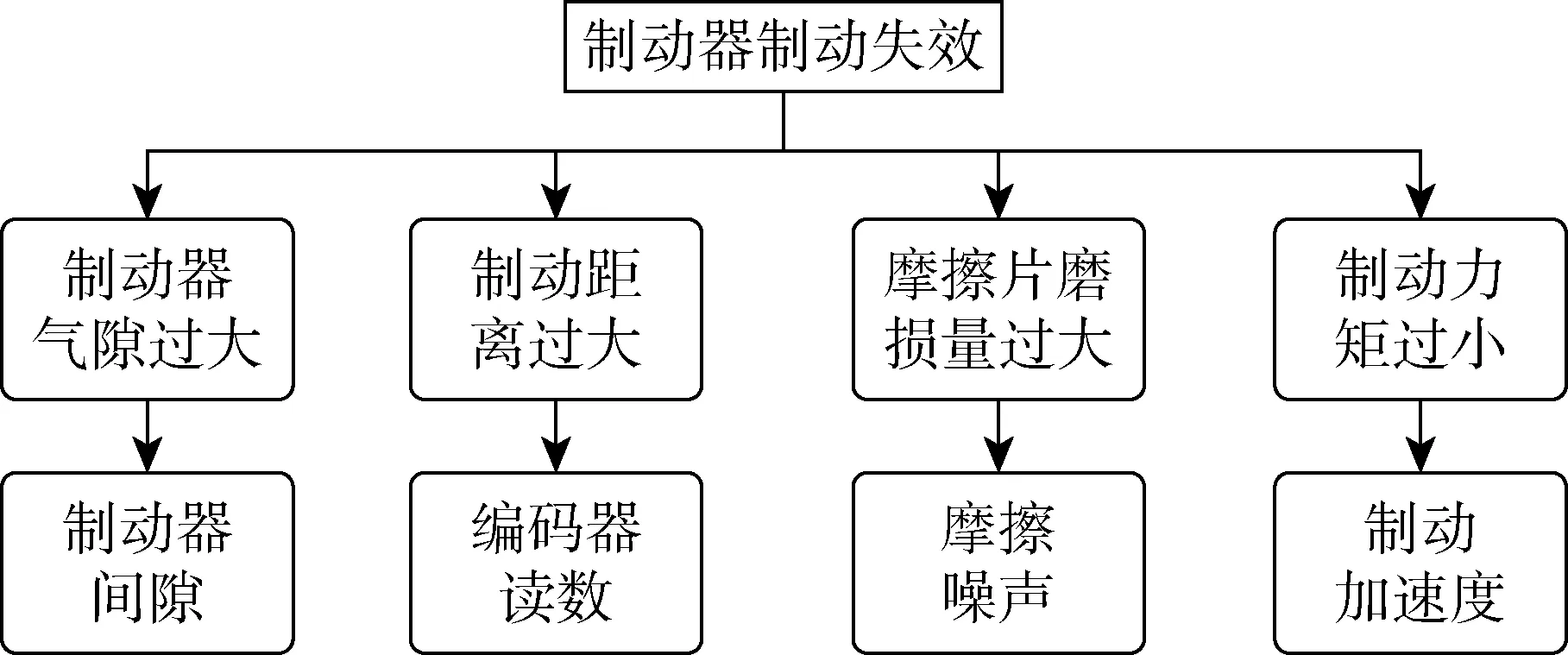
图1 制动器失效分析Fig.1 Failure analysis of brake

2 基于LSTM-ED的剩余生命周期预测算法

根据电梯制动器制动衰退的成因，提出一种基于LSTM-ED的剩余生命周期预测算法.利用长短期记忆(LSTM)网络对数据进行重构处理，将重构误差作为数据的特征序列，通过非线性的全连接层将特征序列映射成剩余生命周期，并利用真实剩余生命周期对回归模型进行训练.不同于典型的迁移学习方法，以 LSTM-ED为特征提取器可以直接将传感器数据在时间轴上的异常反映在特征领域上，LSTM-ED可以根据不同设备的初始状态进行微调，因此特征领域具备对不同型号设备的泛化性.

2.1 LSTM 网络单元

LSTM网络单元是一种循环单元，其通过输入层、上一时刻的隐藏层和记忆细胞层计算当前时刻的隐藏层.该单元结合了记忆细胞层、输入门、忘记门和输出门，能够决定是否需要使用输入门记住输入，何时需要使用忘记门保留记忆，以及何时需要使用输出门输出记忆.为便于表示，将Tn1,n2:Rn1→Rn2表示为矩阵W和适当维度的矢量b做运算z→Wz+b.在t时刻的输入门(it)、忘记门(ft)、输出门(ot)、隐藏层(at)和记忆细胞层(ct)，由输入层(xt)和上一时刻的隐藏层(at-1)以及记忆细胞值(ct-1)计算得到：

(1)

ct=ftct-1+itgt

(2)

at=ottanh(ct)

(3)

式中：gt为新的记忆细胞候选值；m为输入维度；n为隐藏层维度；σ(x)和tanh(x)可以表示为

tanh(x)=2σ(2x)-1

其中：x为任意变量.4个变量的推导公式可以由以上简化矩阵符号得到，如

it=σ(W1xt+W2at-1+bi)

不再赘述.

2.2 重构模型

自编码(ED)重构模型可以通过网络输出与输入向量维度相同的向量，因此可以检测输入数据中的异常值.利用自编码的异常值检测特性，将健康状态下的数据重构误差最小化以提取传感器数据中的异常值特征，从而提高预测精度.

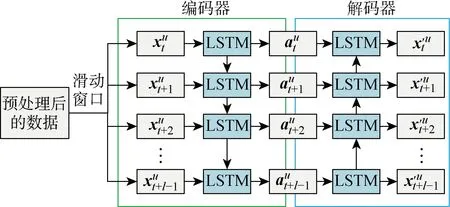
图2 LSTM-ED重构原理Fig.2 Reconstruction principle of LSTM-ED

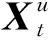
各个时刻的重构误差为

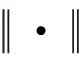
(4)

将损失函数优化至规定的阈值以下得到更新后的LSTM-ED网络，则新网络可以重构出健康状态下的传感器数据.当设备制动衰减时，传感器数据会随机产生异常值，导致重构序列与原始序列之间会存在较大差异，因此需要将X′u与Xu的各元素进行方差处理：

2.3 基于全连接神经网络的回归算法

(5)

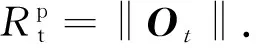
(6)

式中：Rt为真实寿命.

3 无监督的深度迁移学习

在实际预测过程中，通常仅有少量初始状态为有标注的数据和无标定的数据，因此将训练好的网络运用到新设备上并对其进行预测具有一定挑战性.对此，提出一种无监督的深度迁移学习法.

3.1 相关概念

在UDTL中，假设在源领域内均为有标注的数据，则源领域为

(7)

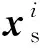
此外，假设在目标领域内标签是不可得的，则目标领域为

(8)

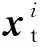
源领域和目标领域分别遵循概率分布P和Q.由于源领域和目标领域的传感器数据分别于不同的电梯制动器设备中采集得到，所以这些数据存在严重的分布差异，导致2.2节中的智能诊断模型不再适用.对此，利用UDTL减少源领域和目标领域之间的特征分布误差，从而在目标领域内实现准确的寿命预测.

3.2 最大平均差异

最大平均差异(MMD)是一种用于测量两个数据集之间分布差异的非参数距离度量，当两个样本的MMD距离足够小时，可以认为分布相同.当Xs和Xt分别遵循概率分布P和Q时，两个数据集之间的MMD距离为

DH(Xs，Xt)=

(9)

式中：sup(·)为输入聚合的上确界；H表示再生核Hilbert空间(RKHS)；φ(·)为从原始特征空间到RKHS的非线性映射；E(·)为数学期望.通过对RKHS的非线性映射，评估两个数据集分布之间的相似程度.由式(9)进一步运算得到

(10)

式中：k(·,·)为特征核函数.线性核函数、多项式核函数和高斯核函数为常用的核函数，而高斯核函数可以实现非线性映射且对于多维数据的计算量较小，因此选择高斯核函数进行运算，即

式中：σ为速度参数，σ越大，则高斯核函数的局部影响范围越大.本文选取σ=5.

3.3 深度迁移学习

3.3.1权重迁移 在源领域内的LSTM-ED深度特征提取网络中提取训练好的权重和偏置，并直接迁移至目标领域中的新LSTM-ED网络中，将其作为新深度特征提取网络的初始权重和偏置：

(11)

(12)

3.3.2特征迁移 经权重迁移后，Xt可以通过新的LSTM-ED提取特征

Ht=L(Xt)

其中：L(·)为LSTM-ED的处理函数；Ht为目标领域的特征序列.因此，源领域的特征序列(Hs)与Ht的迁移误差(LMDD)可由MMD标量表示为

(13)

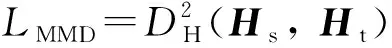
特征迁移使得目标领域与源领域的特征序列分布一致，因此由源领域数据的先验知识训练得到的回归预测全连接网络可以直接作用于新目标特征序列上，从而得到高精度的预测结果.

4 算法训练和预测过程

迁移学习算法的整体框图如图3所示.算法的损失函数为

图3 迁移学习算法框图Fig.3 Overall block diagram of transfer learning

L=αLrec+βLMMD+γLR

(14)

式中：α、β和γ为3个损失函数的修正系数.

典型的迁移学习多采用将目标领域和源领域的数据整合在一起训练，即将α、β和γ均设为非零值进行联合训练.该训练模式未考虑各损失函数的实际意义，易导致对源领域数据的过拟合，而对目标领域数据的预测结果不理想[9].此外，该方法需要完整的目标领域数据，因此在实际运用中无法对目标领域设备进行在线预测.对此，提出一种分步训练方法，其通过保证各模块的准确性实现RUL精准预测，具体步骤如下：

步骤1令β=γ=0，将源领域中前10%的数据作为健康状态数据输入，从而更新LSTM-ED网络的权重和偏置.根据训练得到的重构网络，将输入序列转化为与输入等长的特征序列，并将这一过程定义为特征提取.

步骤2在进行回归预测训练时，令α=β=0，即将源领域数据的回归误差作为更新权重的损失函数，同时固定LSTM-ED的权重不变，仅更新全连接层的权重和偏置.

步骤3权重迁移利用源领域学习得到的LSTM-ED网络和全连接网络，初始化目标领域网络.通过特征提取模块，将新得到的目标领域序列转化为Ht，并将Ht与Hs进行领域适应，即令α=γ=0，利用损失函数更新LSTM-ED，从而减小Ht与Hs的分布误差.

步骤4LSTM-ED网络能够针对目标领域数据进行传感器异常监测，因此利用由步骤3更新后的LSTM-ED参数得到新特征序列，并将其输入到全连接网络中得到当前预测的RUL.本文预测的RUL值均小于1，其含义为剩余生命周期占总生命周期的比例.若预测值小于90%，则直接将其作为该点的RUL值；若预测值大于90%，则说明该时间段内的数据为电梯制动器前10%的健康生命周期数据，需要根据LSTM-ED的异常值检测特性，令β=γ=0、α=1，再次训练更新LSTM-ED参数，并利用新LSTM-ED得到新特征序列，将其作为全连接网络的输入值，重新预测该点的RUL.

其中，步骤1和2为利用源领域数据进行训练网络，完成之后即可得到针对源领域数据的高精度RUL预测算法.步骤3和4为借助目标领域数据进行在线微调训练并得到预测结果.

5 实例分析

5.1 数据介绍

仿真试验平台由迅达曳引机、PLC控制柜和变频器组成，如图4(a)所示.其中，a为加速度，D为制动距离，d为间隙，LI为声强级，N为运行次数.变频器和制动器(110 V直流电压)联动能够加速制动器的制动失效，从而仿真制动器制动力不足的失效模式.基于上述方法，采集得到制动器从初始状态运行至失效的全生命周期数据(见图4(b))，并将其作为源领域数据.当制动器在宁波申菱电梯塔(见图5(a))运作时，人工定期检查得到制动器从初始状态运行至失效的全生命周期数据(见图5(b))，并将其作为目标领域数据.利用源领域数据训练模型，并基于所提迁移学习法实现对目标领域的RUL精确预测.

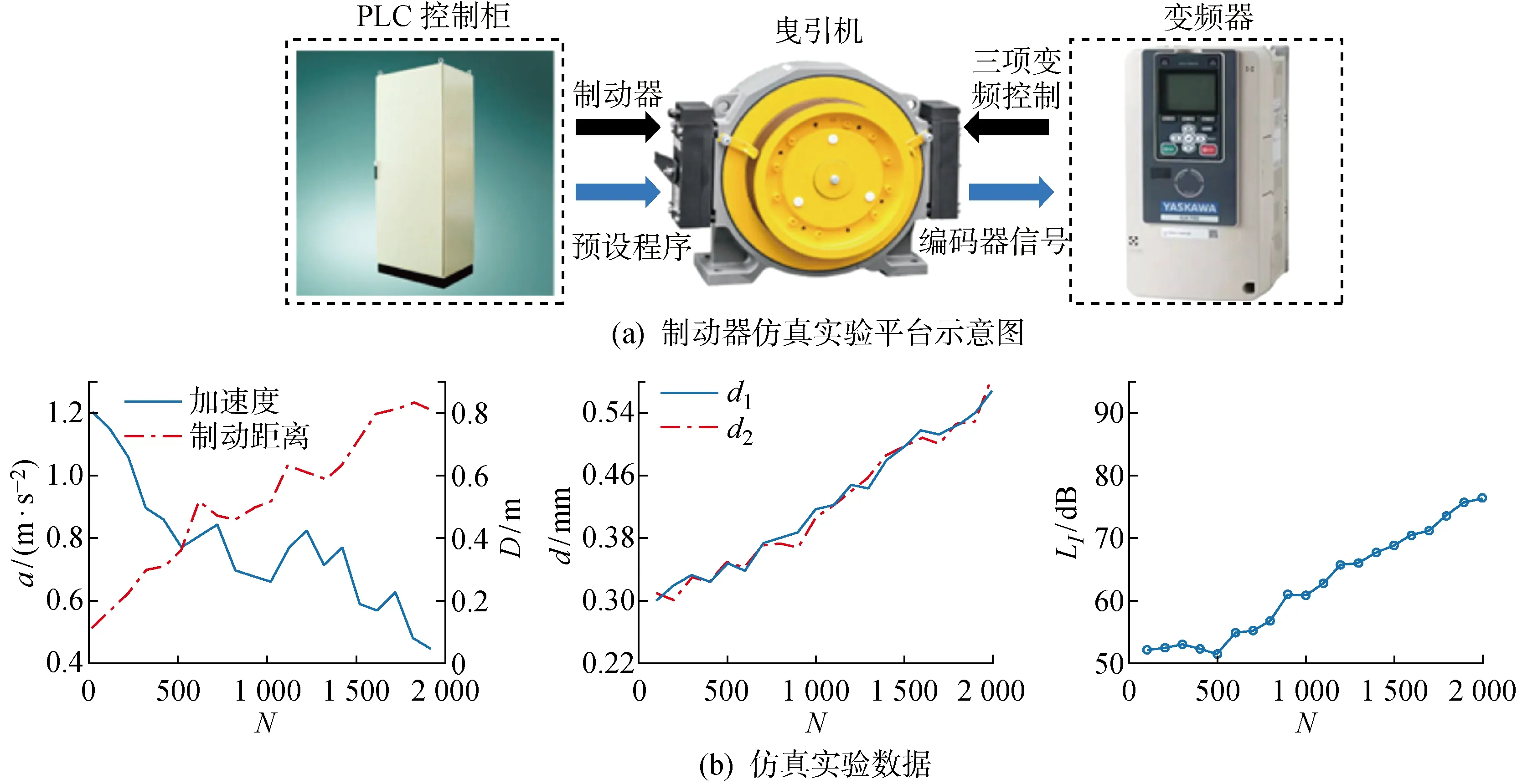
图4 制动器仿真实验Fig.4 Simulation experiment of brake

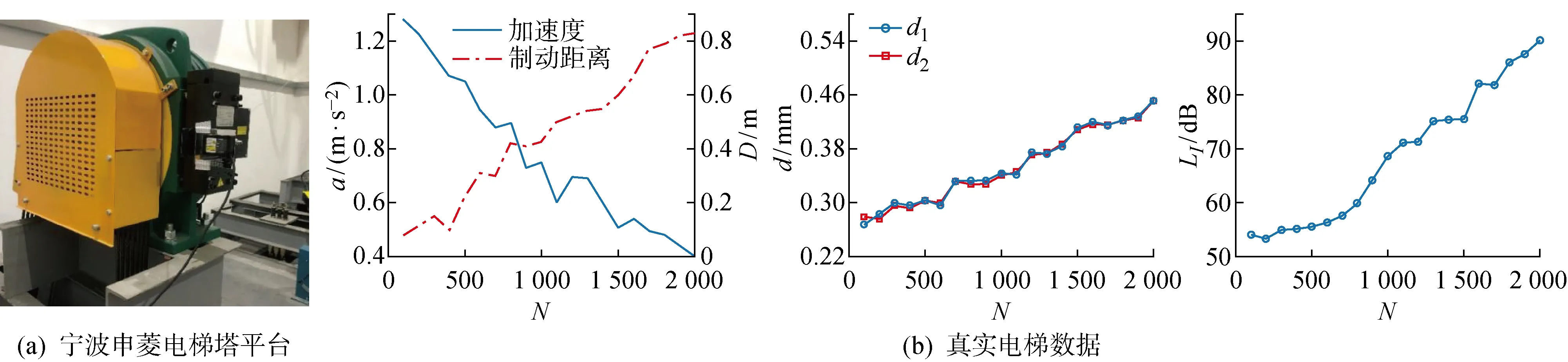
图5 宁波申菱电梯塔实验Fig.5 Shenling elevator tower experiment in Ningbo

5.2 算法结果

利用传感器网络连续采集制动器间隙、编码器读数、摩擦噪声和制动加速度等相关物理参数，并将数据预处理为多个长度l=50的子序列作为网络输入，即输入为5×50个节点(两个制动间隙).LSTM-ED网络分为输入层、隐藏层和输出层，分别输出30×50个节点、20×50个节点和5×50个节点.截取仿真数据中前10%的数据作为健康数据，对LSTM-ED进行训练，并利用训练好的网络将传感器数据投射到如图6所示的特征区域中，其中F为经学习得到的特征值，ε为运行进度(运行时间占总寿命的比例).可知，5个特征值(F1～F5)随时间的增加而增大，且增大趋势相似，表明LSTM-ED可以作为特征提取器并有效地反映制动器衰退现象.

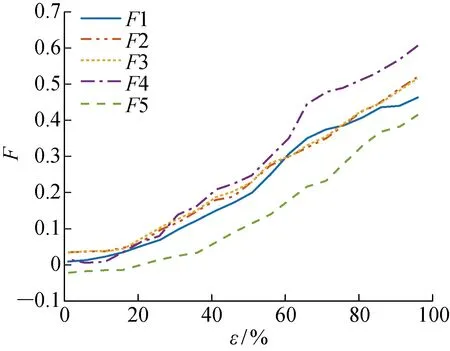
图6 仿真实验数据提取得到的特征Fig.6 Features of simulation experiment data

利用全连接网络(输入层为提取特征，隐藏层包括20个节点，输出层为一维)对LSTM-ED提取的特征进行回归预测，并利用仿真数据中的真实寿命训练全连接网络.经训练后，仿真数据的损失函数降低至小于0.015，即得到针对源领域数据的高精度RUL预测算法.

利用在线微调方法(步骤3和4)，进一步训练LSTM-ED的特征提取器参数，并基于新的特征提取器将电梯塔中的数据转化为如图7所示的特征数据.可知，该提取器同样可以作为特征提取器并有效地反映制动器衰退现象.

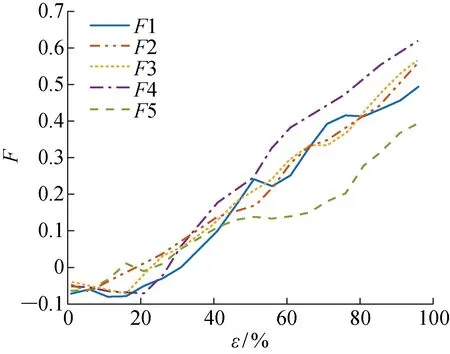
图7 电梯塔数据通过UDTL学习得到的特征Fig.7 Features of elevator tower data learned through UDTL

在预测过程中，利用全连接层预测回归得到的特征，预测结果如图8所示.可知，RUL的预测曲线与真实曲线的吻合度较高.为量化UDTL的预测结果，引入平均绝对值误差(MAE)、均方误差(MSE)和均方根误差(RMSE)：

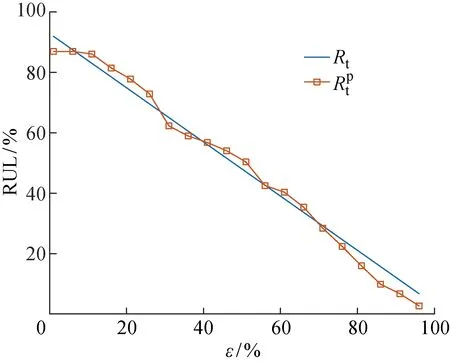
图8 UDTL对电梯塔的剩余生命周期预测Fig.8 RUL prediction of elevator tower by UDTL

(15)

(16)

(17)

根据上式计算得到：MAE=0.03、MSE=0.001 6、RMSE=0.04.可知，利用UDTL预测的误差均很小，表明本文提出的UDTL可以有效预测真实工况下的电梯制动器剩余生命周期.

5.3 对比分析

为证明所提方法的有效性，将未进行迁移学习的预测算法和传统训练法作为对比，进行电梯塔数据的RUL预测，结果如图9所示.可知，与图8中的UDTL方法相比，图9中各方法的预测误差均较大.

图9 电梯塔剩余生命周期预测结果Fig.9 RUL prediction of elevator tower

利用上节所述量化方法，计算不同方法下电梯塔的RUL预测误差，结果如表1所示.可知，在MSE方面，本文所提UDTL方法较无迁移学习的情况降低了59%，较传统训练法降低了54%，证明该方法能够有效提高电梯制动器寿命预测的准确度.

表1 不同方法下电梯塔的剩余生命周期预测误差Tab.1 RUL prediction error of elevator tower by multiple methods

为验证所提方法的优越性，将其他迁移学习方法作为对比，利用源领域数据对网络进行训练，并在真实情况下对电梯制动器进行RUL预测.引入迁移损失作为迁移学习效果的判断指标，其值为源领域与目标领域的MSE之差，结果如表2所示.

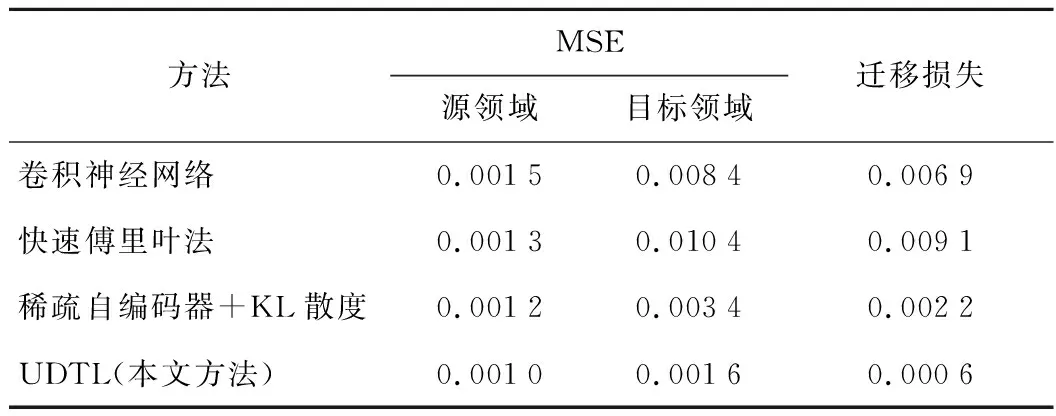
表2 各迁移方法对比结果Tab.2 Comparison results of different migration methods

可知，在保证源领域内的高精度RUL预测的情况下，本文所提UDTL方法的迁移损失值最小，说明其对目标领域电梯制动器的RUL预测结果优于其他方法，迁移过程中的精度损失较低.

5.4 试验结果讨论

分别利用无迁移和经迁移更新后的LSTM-ED对真实工作情况下的电梯制动器进行特征提取，计算特征值总和(Fs)并与仿真制动器提取的特征值总和进行对比，结果如图10所示.其中，仿真制动器的特征标注为制动器1；在真实工作情况下，无迁移和经UDTL迁移更新后的的LSTM-ED提取的特征分别标注为制动器2和制动器3.

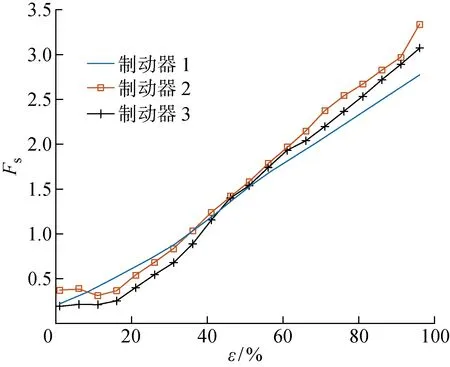
图10 各制动器的特征值总和Fig.10 Sum of eigenvalues of different brakes

可知，在Fs值在大小方面，制动器3与制动器1更接近；在Fs值的变化趋势方面，制动器3与制动器2更接近，即UDTL通过寻找两个制动器的共有特征进行特征的迁移.利用相关度系数(r)量化各特征之间的相关性，其绝对值越大，则相关度越高.

(18)

利用式(18)，得到相关度系数结果，如表3所示.可知，制动器3与制动器1的特征值总和的相关度最高，这表明制动器1通过迁移将特征保留在了制动器2的特征中，从而进一步证明所提方法可以有效提高电梯制动器在真实工作情况下的RUL预测准确度.

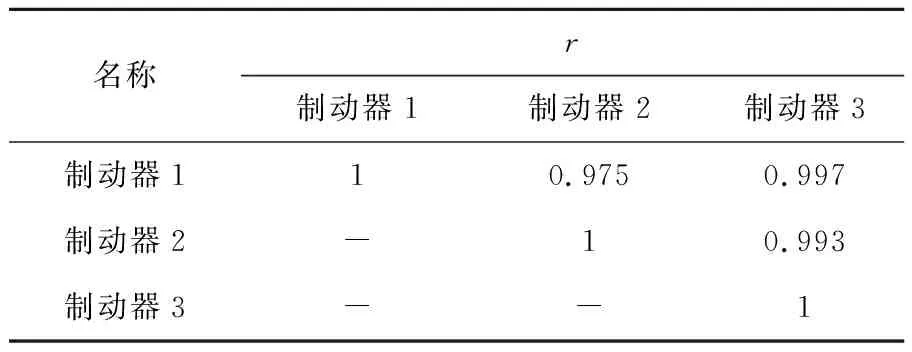
表3 相关度系数结果Tab.3 Results of correlation coefficient

6 结语

为改善电梯制动器在真实工作情况下的寿命预测效果，提出一种基于无监督深度迁移学习的制动器RUL预测方法.该方法利用LSTM-ED将原始数据映射到特征空间中，通过MMD实现真实数据与仿真数据的对齐，最终利用全连接网络进行回归并完成预测.试验和量化数据表明：该算法RUL预测值的均方误差仅为 0.001 6，比无迁移学习的情况降低了59%；其可以对真实工作情况下的电梯制动器进行高精度寿命预测，有助于提升电梯等同类特种设备的安全性.