具有阶段结构的随机传染病模型的灭绝性

刘 娟，陈 功

(蚌埠学院 理学院，安徽 蚌埠 233030)

利用微分方程建立数学模型研究传染病传播过程中的特征是生物数学的重要组成部分，随着传染病建模思想的快速发展，大量不同类型的传染病模型被提出.Alexander M E等[1]研究了一类SIRS传染病模型的分支现象；Wen L S等[2]分析了具有临时免疫的时滞SIRS模型的全局稳定性；Acedo L等[3]通过数学模拟，得出了一类流行病模型的精确全局解；Zhang T L等[4]讨论了具有阶段结构的时滞SIRS流行模型Hopf分支及稳定性；Hou J等[5]研究了接种行为对一类具有饱和发生率SEIR传染病模型的影响；梁桂珍等[6-7]对具有Logistic增长的传染病模型的稳定性进行了分析并考虑了最优控制策略.Liu J等[8]研究了一类具有阶段结构的SIRS模型：

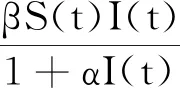
在已有的研究传染病模型的文献中，大多数为确定型模型，没有考虑到现实生活中的随机干扰因素，事实上，在确定型传染病模型中加入环境噪声代表的干扰因素更能反映传染病的实际传播规律.相对于确定型传染病模型，加入随机噪声得到的随机传染病模型会使模型的许多性质发生变化，如使原来稳定的系统变得不稳定，环境噪声可以使系统中持续存在的群体消失.近年来随机微分方程理论的快速发展为研究随机模型提供了理论基础，刘变红等[9]研究了一类具有媒体报道的随SIRI传染病模型，利用It公式和Lyapunov函数等方法,证明了该系统全局正解以及地方病平衡点的存在唯一性；李淑一等[10]研究一类含Ornstein-Uhlenbeck过程的随机SIS传染病模型，并建立了疾病的灭绝性和持久性的判别条件；周艳丽等[11]研究了一类具有非线性发生率和时滞的随机SISV传染病模型，证明了随机模型存在全局唯一正解.因此本文在文献[8]的基础上，考虑到环境噪声的影响，引入随机扰动项，假设环境噪声主要影响接触率β，得βdt→βdt+σdB(t)，B(t)为标准Brown运动且B(0)=0，σ2为环境噪声强度.将接触率β改变后得到模型(2)，本文将利用随机微分方程理论研究正解的存在性、唯一性及疾病消失的充分条件.

1 模型正解的特征

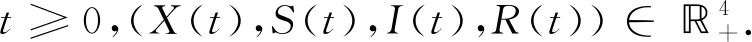
证明要证明随机微分方程有唯一解，由解的存在唯一性定理知方程必须满足利普希茨条件和线性增长条件[12].显然，模型(2)不满足利普希茨条件.为此对含有I(t)的表达式变形，设I=ev(t)，即v(t)=lnI,由It公式可得

则将模型(2)变为

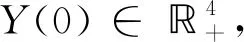
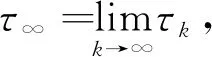
P{τ∞≤U}>ε,

成立，于是存在k1≥k0，当k≥k1时，有P{τk≤U}>ε.

将模型(2)4个等式两边相加得

d(X+S+I+R)=[A-μ(X+S+I+R)-εI]dt≤[A-μ(X+S+I+R)]dt.

对方程

d(X+S+I+R)=[A-μ(X+S+I+R)]dt,

由Y(0)=(X(0),S(0),I(0),R(0))，可得

为了应对繁重的飞行任务，已经年过半百的程凤萍还参与了各类健身运动来锻炼身体，时刻保持旺盛的精力。具有执飞A320、A321、A319三种机型资质的程凤萍现在已经是乘务长和带飞教员，她告诉人民交通网：“不管有着怎样的心情，只要一穿上乘务员的制服后，我就可以立马找到感觉。我热爱这个职业，是这个职业给我带来自信、自豪、自强，只要政策允许，我希望我能够飞到六十岁！”

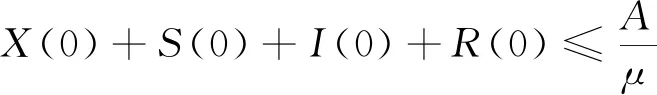
为模型(2)的正不变集.

定义V(X,S,I,R)=(X-1-lnX)+(S-1-lnS)+(I-1-lnI)+(R-1-lnR)，设T>0，则对任意的t:0≤t≤τk∧T，由It公式得

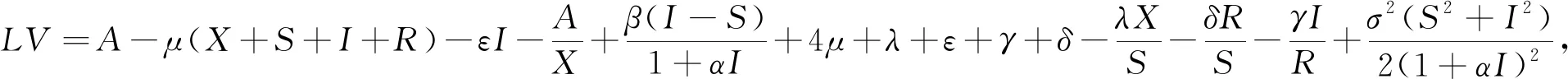
LV≤A+βM+4μ+λ+ε+γ+δ+σ2M2:=K,

(6)

对式(7)两边取0到τk∧T的积分，再取期望得

V(X(0),S(0),I(0),R(0))+KE(τk∧T)≤V(X(0),S(0),I(0),R(0))+KT.

(8)

式(8)中E为期望，对所有的k≥k1，有P{τk≤T}>ε.由于对于每一个ω∈{τk≤T}，X(τk,ω),S(τk,ω)，I(τk,ω)，R(τk,ω)这4个分量中至少有1个等于k或1/k，故有

V(X(τk,ω),S(τk,ω),I(τk,ω),R(τk,ω))≥(k-1-lnk)∧(1/k-1+lnk).

由式(8)得

V(X(0),S(0),I(0),R(0))+KT≥E[1Ωk(ω)V(X(τk,ω),S(τk,ω),I(τk,ω),R(τk,ω))]≥

ε[(k-1-lnk)∧(1/k-1+lnk)].

其中Ωk={τk≤T}，1Ωk(ω)为Ωk的示性函数，令k→∞，得V(X(0),S(0),I(0),R(0))+KT=∞,

故假设不成立，因此τe=∞a.s.得证，则模型(2)存在唯一的全局正解.

2 模型中疾病的灭绝性

下面研究模型(2)中，疾病消失的充分条件，对此有如下的定理.

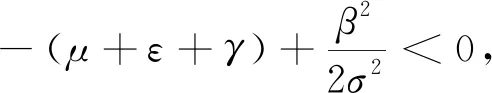
证明利用It公式，将模型(2)中含有I(t)的表达式变为

对上式将两边从0到t积分，再除以t，可得

变形为

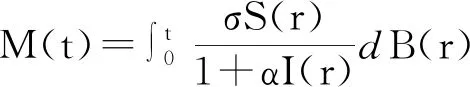
定理2表明如果作用在系统中的白噪声足够大，满足定理的条件，疾病将消失.

3 结论

在文献[8]的基础上加入随机扰动项，利用李雅普诺夫泛函方法研究了具有阶段结构的SIRS模型正解的存在性、唯一性，并得到了疾病消失的充分条件，结果表明，环境噪声对于随机传染病模型有着重要的影响，当噪声强度σ2很大时，染病者群体I(t)将消失，即疾病将灭绝.定理说明了外部环境对于生物系统的影响很大，研究随机模型具有一定的现实意义.