基于融合局部信息的全局划分活动轮廓模型在图像分割中的研究
2021-12-05熊点华唐利明
熊点华,唐利明
(湖北民族大学 数学与统计学院,湖北 恩施 445000)
图像分割是人们根据需求,将图像分成一个或多个轮廓的过程,其中每个轮廓互不相交,且所有轮廓的并集就是图像本身.每个轮廓性质不同,可据此提取出有价值和意义的特征(或区域)[1-2].
关于图像分割的方法有很多,其中基于水平集的活动轮廓[3-4]图像分割方法计算稳定、分割精度高和评价体系完整,因而受到广大研究者的关注.现有的活动轮廓模型可分为基于边缘[5-6]和基于区域[7-8]的两类,相比于基于边缘的活动轮廓模型,基于区域的活动轮廓有较好的实验效果,且对噪声具有一定的鲁棒性,因此成为研究的主流方向.经典的活动轮廓模型是Chan和Vese[9]提出的CV模型,该模型对初始轮廓鲁棒,且对噪声的鲁棒性较好,但CV模型将目标和背景的灰度近似为常值,使得CV模型不能分割灰度不均图像.Li等[10]提出的局部二值拟合能量(Local Binary Fitting,LBF)模型能分割灰度不均图像,但以高斯核函数选取局部窗口,使得LBF模型对噪声的鲁棒性较差,且对初始轮廓敏感.为了使融合局部信息的活动轮廓模型对初始轮廓鲁棒,Wang等[11]结合了CV和LBF模型的优点,提出了局部和全局灰度拟合(Local and global intensity fitting,LGIF)模型,LGIF模型能分割灰度不均图像,且对初始轮廓的敏感性降低,但权重系数受初始轮廓位置的影响,限制了该模型的应用.Han等[12]用Jeffreys散度构造新的局部和全局能量项,并基于迭代次数构造了一个自适应函数,实现了全局与局部能量的权重系数的自动选取,但该模型仅利用图像的灰度来驱动曲线演化,未充分考虑图像的纹理等信息.Zhang等[13]基于图像恢复的全变分(Total Variation,TV)模型[14],在CV模型中引入多尺度项,提出多尺度CV(Variational Level Set Model for Multiscale,MCV)模型,该模型通过增大尺度参数将图像的噪声和纹理去掉,从而实现图像分割,但MCV模型的能量提取项为CV模型中的能量项,导致MCV模型不能分割多相图像,且对强度大的噪声较敏感.Min等[15]结合图像的纹理特征,构建划分函数,提出了基于强度-纹理的水平集方法(Intensity-Texture model based level set method,ITLSM)模型,ITLSM模型能很好地分割纹理图像,但对灰度不均的自然图像的分割结果较差,对图像灰度值敏感.
为了分割灰度不均图像,受ITLSM[15]和LBF[10]模型的启发,提出融合局部信息的全局划分的活动轮廓(DGLF)模型,实现了对权重系数的自动选取并保持模型对初始轮廓的鲁棒性.首先将ITLSM的能量项与LBF的能量项进行项线性组合,然后基于迭代次数构建一个自适应函数,作为全局与局部能量的权重系数.DGLF模型具有如下优势:① 在全局划分能量中融入局部能量,使得模型能分割灰度不均图像,对初始轮廓鲁棒;② 基于迭代次数建立自适应权重函数,实现轮廓演化中全局与局部能量的自动选取;③ 使用JS系数作为评价指标,充分说明DGLF模型的分割效果.
1 研究背景
1.1 LBF模型
为了分割灰度不均图像,Li等[10]提出了LBF模型,利用局部二值拟合能量并引入高斯核函数来分割灰度不均匀的图像,从而对灰度不均匀的图像实现目标边界的提取.LBF模型中的能量泛函如下:
ELBF=EL+ER,
(1)

对式(1)极小化求得f1(x)和f2(x)的稳态解:
另外,采用梯度下降法[16],求解(1)式得水平集的演化公式如下:
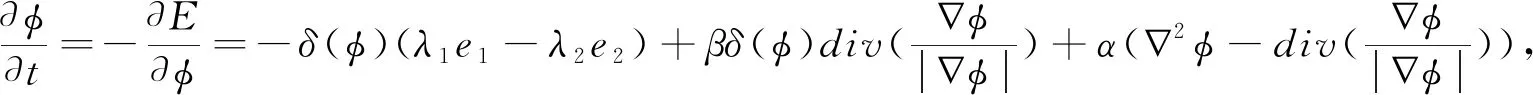
在实际应用中,LBF模型能很好地分割灰度分布不均匀的图像.但是由于该模型结合了图像的局部信息,该模型对初始轮廓和噪声敏感.
1.2 ITLSM模型
为分割复杂两相图像,Min等[15]构建划分函数,提出了基于强度-纹理的ITLSM模型.该模型通过引入划分函数,每个区域分为强度值比平均强度值大和比平均强度值小的两个部分,划分函数定义为:
c1为图像目标区域的灰度均值,c2为图像背景区域的灰度均值,x∈Ω.这里使用CV[9]模型中的目标与背景均值分别作为目标与背景区域的灰度均值,c1与c2的计算方式分别如下;
ITLSM模型中的能量项定义为: EITLSM=EDG+ER,
(11)

对式(11)分别求解关于d11,d12,d21,d22的极小值得
通过梯度下降法[16]求解式(11)得零水平集的演化方程:
ITLSM模型基于划分函数,将每个区域分为强度值比平均强度值大和比平均强度值小的两个部分.该模型能分割具有模糊边界的图像,但对ITLSM模型对图像的灰度值敏感,对图像灰度值较大区域的目标拟合能力较弱.
2 DGLF模型
2.1 融入局部信息的全局划分能量项
为了分割复杂的自然图像,并保持能量泛函对灰度不均图像的拟合能力,受到文献[12]和文献[15]的启发,提出将局部信息融入到全局划分活动轮廓模型中,得到DGLF模型,模型中能量泛函的定义如下:
EDGLF=wEL+(1-w)EDG+ER,
(17)
其中,w∈(0,1)为权重系数,使用LBF[10]模型中的能量项EL作为局部能量项,用于捕捉图像的局部灰度变化;使用ITLSM[15]模型中的全局划分能量项EDG作为全局项,用于拟合复杂图像的边界,并保持模型对初始轮廓的鲁棒性.采用梯度下降法[16],求得水平集的演化方程如下:
式中,d11,d12,d21,d22由式(13)和式(14)给出,e1和e2由式(7)和式(8)给出.
2.2 自适应函数

其中,n为最大迭代次数,a为伸缩系数,t为平移系数,实验中选取t=10.w(n)的演化分为3个阶段,函数图像如图1所示.
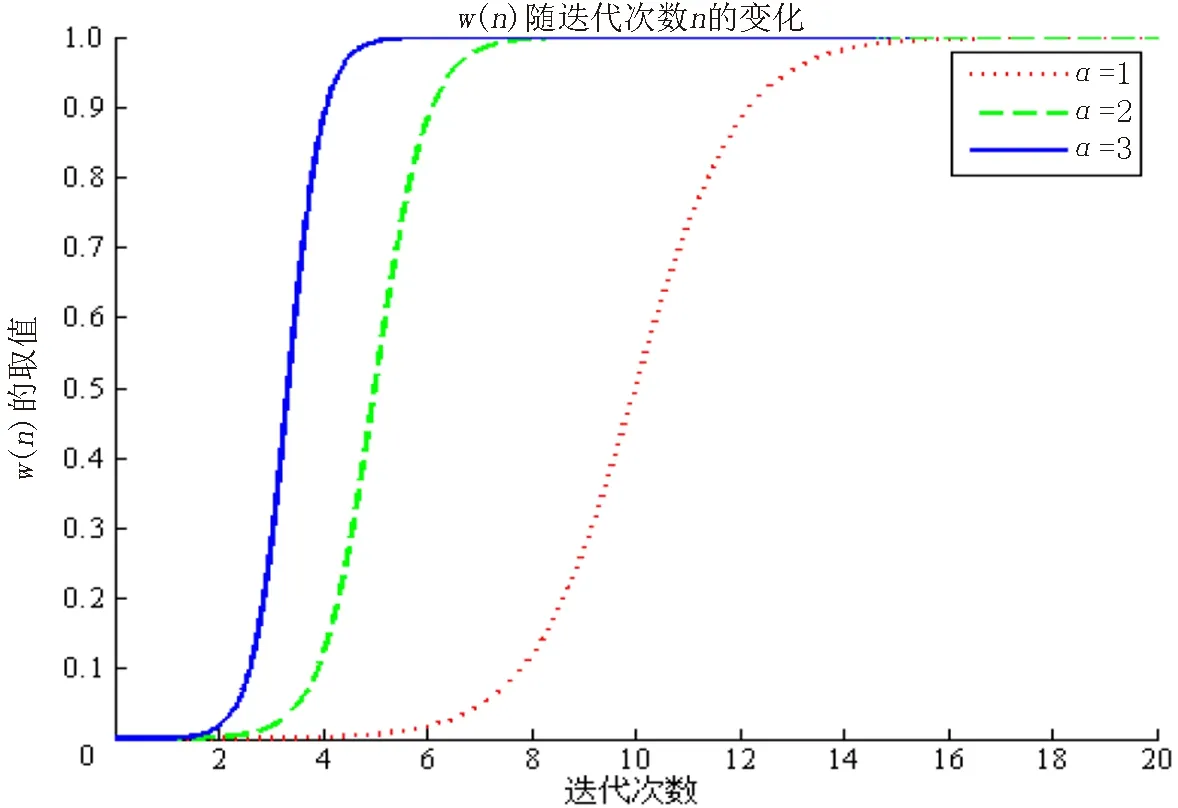
图1 不同取值a下w(n)的曲线
由图1可知,w(n)的曲线演化分为3个阶段.以a=2为例,第1阶段为n∈(0,2),此时权重函数w(n)的值接近于0,由全局划分能量主导轮廓演化,并保持模型对初始轮廓的鲁棒性;第2阶段为n∈(2,6),此时w(n)∈(0,1),由局部能量和全局划分混合驱动轮廓演化,保持局部能量捕捉图像灰度局部变化的能力以及保持全局项拟合图像整体目标的能力;第3阶段为n∈(6,20),此时w(n)的取值接近于1,由局部能量主导轮廓演化,保证模型对图像中的灰度不均区域目标的拟合能力.综合上述3个阶段,自适应函数w(n)实现了对权重函数的自动选择,还保证了模型对初始轮廓的鲁棒性,提高了实验效率.用有限差分法对式(18)进行求解,使用交替迭代数值模拟DGLF模型,DGLF模型的算法如下.
步骤1 输入图像并设置参数α,β,λ11,λ12,λ21,λ22;
步骤2 给定初始轮廓,并设置n=0和最大迭代次数N与自适应函数w(n);
步骤3 通过式(10)计算c1和c2;
步骤4 通过式(14)~(15)计算d11,d12,d21,d22;
步骤5 由式(5)计算f1(x)和f2(x);
步骤6 通过式(17)更新水平集函数;
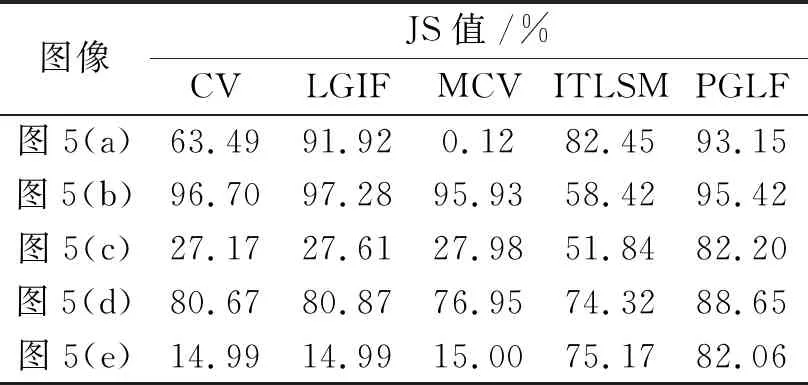
步骤7 当n 实验在LAPTOP-RETV7IRD Aspire A515-516Intel(R) Core(TM) i5-7200U CPU © 2.50 GHz 2.71 GHz RAM 4.0 G matlab2014a环境下进行.实验包括验证模型对初始轮廓的鲁棒性、分割人工合成图像与自然图像,并采用Jaccard(JS)系数作为评价指标.为了有更好的对比度且保持模型对初始轮廓的鲁棒性,实验选取CV、LGIF、MCV和ITLSM模型与DGLF模型作对比(上述模型都对初始轮廓鲁棒).各模型的初始轮廓大小和位置固定为(63∶103,69∶199). 在式(20)中,RS与RG分别为分割结果的二值图与标签图的二值图.RS通过模型分割而得出,RG通过对人工标记图进行二值化而得出.|·|表示图像中的像素点.J(RS,RG)∈[0,1],当RS=RG时,J(RS,RG)取得最大值1,此时分割结果最好;RS∩RG=0时,J(RS,RG)取得最小值0,此时分割结果最差. 在图像分割中,因为扳手有多个孔洞,且有多个目标,因此常用多孔扳手图来验证图像分割模型对初始轮廓的鲁棒性.分别取定初始轮廓位置为包含图像目标(a1)、不包含图像目标(a2)、分别在图像两个目标内部(a3)和(a4)、同时与图像两个目标相交(a5)以及随意选取初始轮廓大小与位置(a6),由图2所示.(a1)~(a6)是带初始轮廓的图像,(b1)~(b6)对应(a1~a6)初始轮廓下的分割结果,(c1)~(c6)是分割结果(b1)~(b6)对应的二值图.实验结果表明,DGLF模型在不同的初始轮廓条件下都能对扳手图有较好的分割结果,且在初始轮廓不同的条件下,DGLF模型对扳手图的分割结果一致,说明DGLF模型对初始轮廓有较好的鲁棒性.分割结果如图2所示. 图2 DGLF模型在不同初始轮廓下的分割结果 选取人工合成图像验证模型的分割能力.因为含低噪声图像(图3(a)和图3(b))和灰度不均多米粒图像(图3(c)和图3(d))含有较丰富的信息,可以很好地验证活动轮廓图像分割模型对图像的分割能力,所以这里选取这两类图像作为分割对象,以验证DGLF模型的分割能力.分割结果如图3所示.由图3可知,DGLF模型对人工合成图像的分割结果较好;另外,由表1可知,DGLF模型分割人工合成图像的JS值都在88%以上;说明DGLF模型对人工合成图像有良好的分割效果. 图3 DGLF模型分割合成图像结果对比 表1 DGLF模型分割人工合成图像的JS值 分割两幅简单动物图像(图4(a)、图4(d))、一幅背景灰度不均(图4(b))和一幅边界模糊(图4(c))的复杂动物图像,并与CV、LGIF、MCV模型对比,分割结果如图4所示.CV、LGIF、MCV模型在分割图4(a)、图4(b)和图4(d)时有较好的分割效果,且分割结果的JS值都较高,但都低于DGLF模型.由于ITLSM模型对图像灰度值敏感,使得ITLSM模型仅能分割出图像4(c),不能分割其他对比图像,由表2可知,ITLSM模型在分割图4(a)、图4(b)和图4(d)时的JS值较低.在分割边界模糊图像(图4(c))时,只有基于划分函数的活动轮廓 (DGLF和ITLSM)模型能有较好的分割结果.由于ITLSM模型未考虑图像的局部信息,使得ITLSM模型的分割能力弱于DGLF模型,分割结果的JS值也低于DGLF. 自然图像是生活中常见的图像之一,对自然图像的分割也极为重 要,因此选取简单(图5(b)、图5(d))、灰度不均(图5(a)、图5(c))和边界模糊(图5(e))的自然图像作为分割对象,验证模型的分割能力,分割结果如图5所示.由图5可直接得出,CV和LGIF模型分割图5(a)、图5(b)、图5(d)时能取得较好的分割效果,但是对灰度不均(图5(c))和边界模糊(图5(e))图像的分割效果较差.MCV模型在分割图像时,有时会把图像中的关键信息误以为噪声而将图像的关键目标去除,导致MCV模型不能分割图像图5(a),且由表3所示,MCV在分割图像图5(a)时JS值仅为0.12%,分割其他图像都与CV、LGIF模型的JS值较为接近.由于ITLSM模型没有考虑图像的局部信息,使得ITLSM模型在分割灰度不均(图5(c))图像时未能捕捉图像的局部灰度变化,但ITLSM模型中的全局划分项对边界模糊(图5(e))图像有较好的分割结果.由于DGLF模型中融合了局部信息,综合图5与表3,DGLF模型对图5(a)~(e)的分割效果较好,且DGLF的JS值更优于文中其他对比模型 (除了LGIF分割图5(b)的JS值较高). 表3 分割自然图像结果的JS值对比 图5 自然图像分割结果对比 融合局部信息的全局划分活动轮廓模型对灰度不均的图像有较好的分割效果,对初始轮廓鲁棒,还实现了对全局能量与局部能量的自动选取.另外,相较于其他几个活动轮廓模型,DGLF模型的JS值较高.但是,DGLF模型中的全局项中含有划分能量项,使得模型对灰度值较大区域的拟合能力较弱,因此后续将构建一个新的划分函数,以提升此类图像分割模型的分割能力.3 实验结果与分析
3.1 Jaccard评价系数
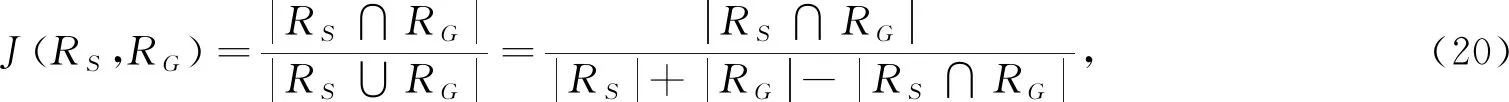
3.2 模型对初始轮廓的鲁棒性

3.3 分割人工合成图像


3.4 分割动物图像
3.5 分割自然图像

4 结论
