水下爆炸船体梁总体响应特性数值模拟
2021-12-03刘丽滨李海涛刁爱民张海鹏杨理华
刘丽滨,李海涛,刁爱民,张海鹏,杨理华
(1. 海军潜艇学院,山东 青岛 266199;2. 海军工程大学舰船与海洋学院,湖北 武汉 430033)
随着精确制导武器的发展,舰船遭受水下非接触爆炸攻击受到了广泛关注。 水下爆炸冲击波主要造成船体局部损伤,而爆炸气泡脉动频率接近舰船的低阶垂向固有频率,易造成船体总体损伤。在水下爆炸冲击波和气泡脉动的联合作用下,舰船的总体响应特性则更加复杂。
水下爆炸作用下的舰船响应研究多集中于中远场爆炸[1-3],而近场非接触爆炸作用下舰船总体响应研究相对较少。随着水下爆炸研究工作的不断深入,针对水下非接触爆炸作用下舰船总体响应的研究逐渐增多[4-8]。Wang 等[9]通过试验与数值模拟相结合研究了船体梁的总体损伤特性,提出了船体梁总体损伤的3 种主要模式;Zhang 等[10]基于Abaqus 建立了水下爆炸作用下船体结构的三维流固耦合模型,研究气穴影响下船体结构的动态响应;李海涛等[11]基于Dytran 有限元软件研究了半封闭船体梁结构的总体损伤特性,初步分析了船体梁发生中垂损伤的机理;王龙侃等[12]基于Abaqus利用LS-DGFDG 方法研究了船体板架结构的近场水下爆炸毁伤特性。
在以上研究的基础上,本研究将以炸药在船体梁中部正下方爆炸为研究对象,利用Abaqus 有限元软件建立水下爆炸作用下全封闭船体梁的数值计算模型,进一步对船体梁的总体响应特性进行分析,初步给出船体梁发生中垂、中拱等损伤模式的条件,为水下非接触爆炸作用下舰船总体响应研究提供参考。
1 缩比船体梁模型设计
以某型船为母型,按照1∶50 几何缩比,设计全封闭、等截面、箱型的船体梁模型。船体梁模型设计主要考虑以下原则:(1) 模型与母型的总纵强度相似;(2) 模型的一阶湿频率与缩比炸药爆炸气泡脉动频率基本吻合。
假设船体梁模型与母型总纵强度相似,距船体梁中性轴y处的应力为

则模型和母型之间存在关系

可转化为

式中:M为参考点相对于中性轴的弯矩,I为船体梁截面的惯性矩, λ为几何缩比系数,下标m 和p 分别表示模型和母型。Ip和yp已知,若模型与母型选取相同材料,则Im与ym的比值恒定,即确定缩比船体梁模型的尺度参数ym,即可得到Im。
忽略原型设备分布对质量分布和总体强度的影响,将其主要结构件质量计入船体板厚,模型不设横向和纵向加强构件。模型结构及主要参数:梁长2.8 m,宽0.3 m,型高为0.08 m,板厚为1 mm,船体梁设置6 个横舱壁,横舱壁之间的距离均为0.4 m,沿模型的纵向安装加速度传感器和应变传感器,其中加速度传感器分别位于距左端1.4、2.0 m甲板边沿处(A1、A2),应变传感器分别位于距左端1.4、1.6、2.0、2.8 m 舷侧上部边沿处(S1~S4),如图1 所示。
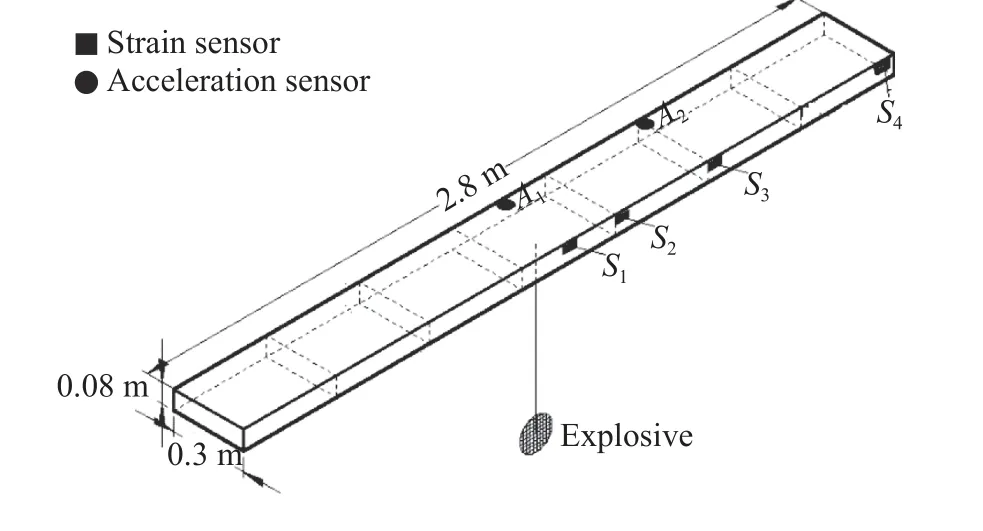
图1 船体梁结构及测点布置Fig. 1 Structure of hull girder and locations of sensors
2 数值模拟方法
2.1 理论基础
采用Abaqus 独有的声固耦合法,通过声学介质模拟流场。假设压力满足小范围变化条件,能够解决水下爆炸模拟和湿模态计算等多种流固耦合问题,则流固耦合控制方程为[13]
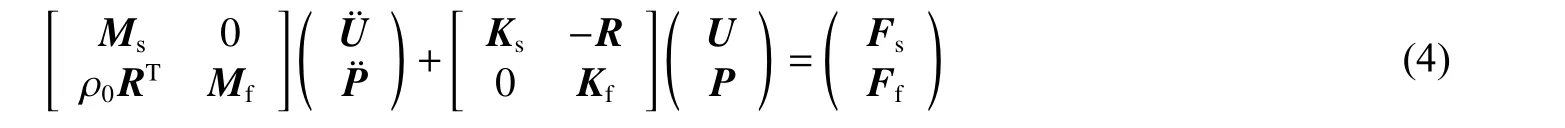
式中:M,K和F分别为质量矩阵、刚度矩阵和载荷矩阵;下标s 表示结构,下标f 表示流体;R为流固耦合矩阵; ρ0为流体密度;U和P分别为节点位移矩阵和流体声学压力矩阵。
2.2 计算模型
为了尽可能还原无限流场,模拟时综合考虑数值计算的精确性和计算时间,流场半径设为船体梁结构半径的6 倍,船体梁流固耦合面附近流场网格取冲击波长的1/10[14],建立船体梁和流场有限元模型,如图2 所示。流场模型分为中间部分和两端部分,中间为半圆柱形,两端为半球形。流场半径为船体梁模型半宽的6 倍,在模型半宽3 倍处对水域模型进一步切分,对网格局部细化处理。船体梁结构单元尺寸为0.02 m,采用四边形单元,单元类型为S4R;流场单元尺寸为0.02 m(局部细化)和0.04 m,采用四面体单元,单元类型为AC3D4。船体梁模型漂浮于水面上,自由液面的作用通过“tie”绑定来定义两者的耦合关系。
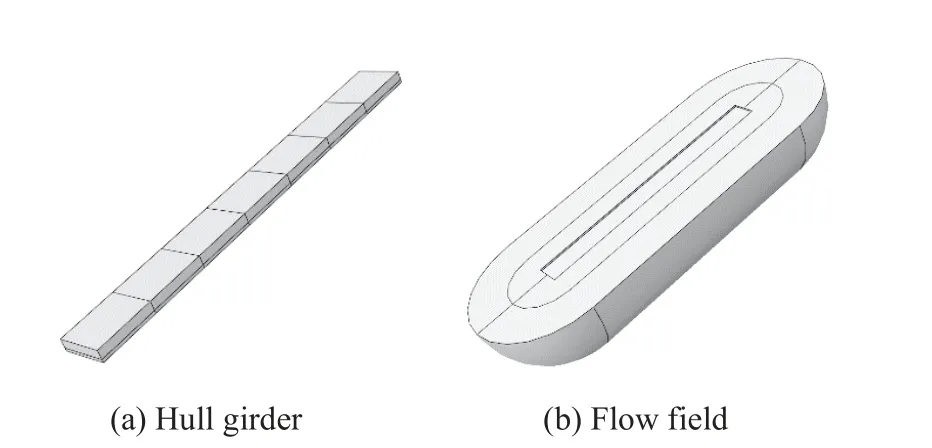
图2 有限元模型Fig. 2 Finite element model
2.3 参数设置
对于爆炸载荷,可通过设置爆炸点及参考点的坐标来表征爆距及入射角,参考点尽量设置在结构最先受到爆炸载荷作用的位置,可以避免模拟失真。爆炸载荷在参考点处输入,载荷可由经验公式计算得到,也可通过试验实测压力数据。数值模拟爆炸载荷由Geer-Hunter 经验公式得出[15]。模型拟采用Q235A 钢,设计吃水0.2 m,其密度为7 800 kg/m3,弹性模量为210 GPa,泊松比为0.3,塑性设置考虑材料的应变率强化效应,采用Johnson-Cook 模型[13]

式中: σ为材料的等效应力; εp为等效塑性应变; ε˙0为初始塑性应变率, ε˙p为等效塑性应变率; θˆ为无量纲温度;A、B、C、n、m为材料参数,一般通过试验来确定,该数值计算中所用的材料参数见表1。

表1 材料参数[16-17]Table 1 Material parameters[16-17]
3 数值模拟工况
通过改变药量、爆距等参数,研究不同爆径比R/r条件下船体梁的总体响应特性,爆炸工况见表2,其中W、R、r、T分别为药量、爆距、气泡最大半径和脉动周期[18]。通过分析船体梁上典型位置的变形情况,得到船体梁结构的总体响应。为尽量消除局部变形对分析总体响应的影响,测点位置选择在上甲板与外舱壁交接位置,测点数量及位置见图1。
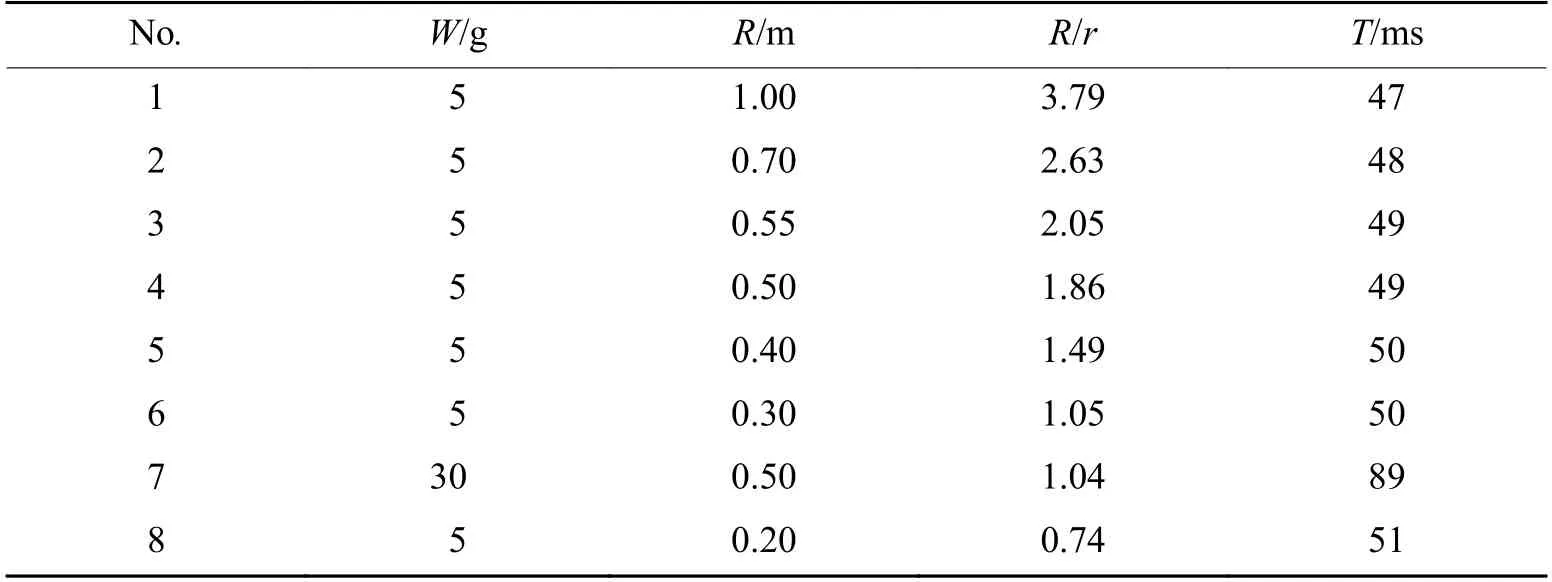
表2 工况相关计算参数Table 2 Calculation parameters of working conditions
4 数值模拟方法的试验验证
在工况1 中,爆炸强度偏小,船体梁表现为全弹性运动;工况2 的爆炸强度增大,船体梁存在弹塑性运动过程。选取工况1 和工况2 作为典型数值计算工况,结合前期开展的缩比船体梁模型试验结果,从船体梁模态、总体变形和中点位移3 个方面进行对比,验证该数值计算方法的合理性。
4.1 模态
船体梁湿模态计算有两种方法:一是计算出船体周围附连水的质量,加载于船体外壳,从而计算湿模态;二是将船体结构和周围流场进行耦合,采用声固耦合法计算湿模态。
采用附连水质量法时,Abaqus 是以MASS 单元形式,将附连水质量按分布情况以质量点的形式布置于船体外壳上,直接利用频率分析计算得到船体的湿模态。采用声固耦合法时,需要建立包围船体梁的整个流场,流场以声学材料定义,先通过“tie”绑定定义两者的耦合关系,再利用频率分析计算得到船体的湿模态。表3 为两种方法的计算结果比较,f1、f2分别为垂向一阶振动和二阶振动的频率。试验测得船体梁一阶湿频率为16.8 Hz,从表3 中数据可以看出,声固耦合法计算的湿频率与试验值更相符。此外,声固耦合法更便于其他分析研究。

表3 湿频率的比较Table 3 Comparison of wet frequencies
4.2 总体变形
图3 为工况1 船体梁模型总体变形试验结果与Abaqus 模拟结果对比。从图3 中可知,在整个水下爆炸过程中,船体梁经历了中拱→中垂→再次中拱的变形过程,呈现明显的一阶上下弯曲变形。通过对比各典型阶段船体梁变形的试验和模拟结果可以发现,无论是时间(t)历程还是变形程度,两者基本一致。

图3 船体梁变形过程的数值计算(a)和试验结果(b)对比Fig. 3 Comparison of numerical simulations (a) and experimental results (b) of the hull girder deformation
4.3 中点位移
图4 给出了工况1 中船体梁中点试验与模拟情况下的位移时程曲线。可以看出,试验和模拟得到的船体梁变形过程基本一致,变形周期和变形位移均相当。就船体梁变形周期而言,船体梁完成一次运动周期(A点→B点)的模拟时间约为53 ms,而完成一次运动周期(A'点→B'点)的试验时间约为50 ms;就变形位移而言,船体梁第一次中拱时,试验中模型较原始状态的变形位移约为1.2 cm,模拟的位移约为0.7 cm,第一次中垂时的模拟位移和试验位移均约为0.9 cm。综合分析可知,模拟值与试验值吻合较好,存在少许误差的原因可能是模拟中未考虑船体梁结构阻尼,阻尼会吸收水下爆炸能量,表现为结构响应滞后和运动周期缩短。
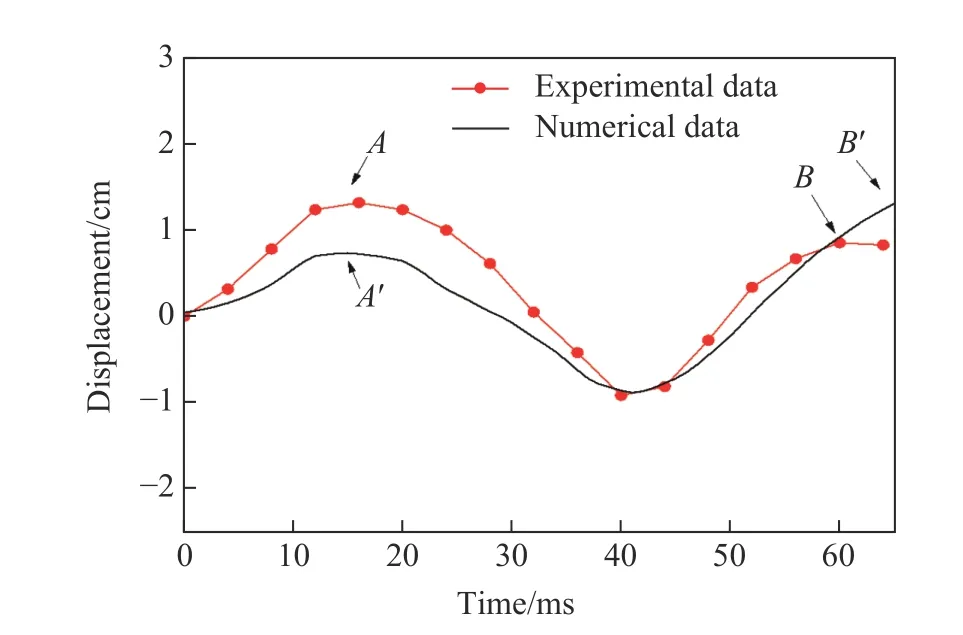
图4 工况1 船体梁中点位移的试验和数值模拟结果对比Fig. 4 Comparison of experimental and numerical results of the girder’s midpoint displacement in case 1
图5 为工况2 中船体梁中点的位移时程曲线,与工况1 类似,模拟曲线与试验曲线吻合良好。可以看出,相较于工况1,工况2 爆距减小,爆炸冲击作用更加剧烈,中拱和中垂阶段的位移峰值均明显增加,尤其是中垂阶段位移幅值增加更明显。
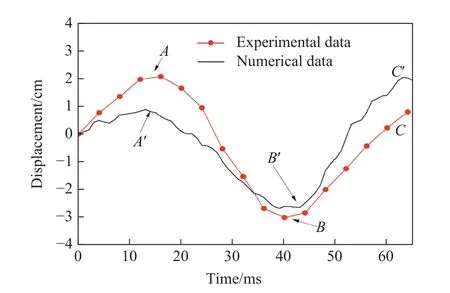
图5 工况2 船体梁中点位移的试验和数值模拟结果对比Fig. 5 Comparison of experimental and numerical results of the girder’s midpoint displacement in case 2
综合上述分析可知,该数值模拟方法具有合理性,可为研究船体梁的总体响应特性提供参考。
5 响应分析
5.1 变形分析
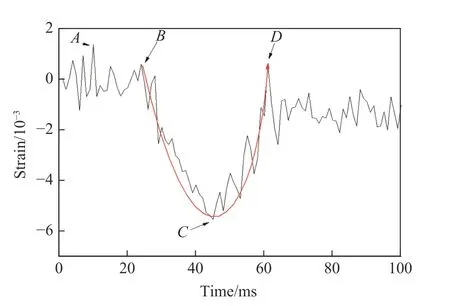
表4 为不同工况下船体梁的变形情况,其中:fb和fB分别为气泡脉动频率和船体梁一阶湿频率;sh表示船体梁第一次中拱变形位移,sh2表示船体梁第2 次中拱变形位移,ss表示船体梁第一次中垂变形位移,Dynamic responses 为船体梁最终损伤模式。船体梁的一阶湿频率fB为19.6 Hz。可以看出:当fb/fB接近1 时,随着R/r减小,船体梁响应由鞭状运动向中垂损伤转变;当1 表4 不同工况下船体梁的变形情况Table 4 Final deformation of hull girder in various cases 选取工况6、工况7 作为典型工况分析船体梁结构的应变情况。图6 为工况6 船体梁中点(测点S1)的应变时程曲线。从图6 中可以看出,船体梁模型出现了4 个明显的应变峰:A点为冲击波作用所致中拱应变峰;B点为气泡膨胀所致滞后流推动船体梁进一步中拱的应变峰;C点为气泡脉动过程中流场负压所致船体梁中垂应变峰;D点为气泡溃灭射流造成船体梁再次中拱的应变峰。BC段应变值迅速减小,达到最低5.5×10−3,说明气泡负压弯矩对船体梁中垂作用明显且剧烈;CD段应变值迅速增加,说明气泡收缩溃灭对船体梁冲击作用也十分明显;D点后船体梁有稳定的轻微中垂变形,S1测点存在一定残余应变,局部板格屈曲变形。 图6 工况6 中S1 测点的应变时程曲线Fig. 6 Strain-time history of point S1 in case 6 图7 为工况7 中测点S1和S4的应变时程曲线。工况7 与工况6 中测点S1的应变变化规律基本相同。图7(b)为测点S4的应变时程曲线,B点应变峰说明工况7 下船体梁中垂响应明显,测点上甲板局部板格屈服,受挤压向下凹陷。图8 和图9 分别为工况6 和工况7 船体梁最终总体变形和局部结构屈服情况。可以看出,测点处的应变时程曲线能较好地反映船体梁变形情况,包括板壳局部结构屈服情况。 图7 工况7 下测点S1 和S4 的应变时程曲线Fig. 7 Strain-time histories of points S1 and S4 in case 7 图8 工况6 中总体及局部变形Fig. 8 Overall and local deformation in case 6 图9 工况7 中总体及局部变形Fig. 9 Overall and local deformation in case 7 不同工况下梁结构的加速度响应基本相似,图10 为工况1 中测点S1的加速度时程曲线。可以看出:在冲击波作用阶段,结构加速度响应非常明显,且主要以高频为主;而在气泡作用阶段,结构加速度峰值相对较小,约为冲击波阶段的15%;爆炸载荷作用结束后结构仍有小幅值加速度,且幅值变化不大,说明爆炸载荷作用结束后结构仍存在较长时间的自由振动。 图10 工况1 中测点S1 的加速度时程曲线Fig. 10 Acceleration-time history of point S1 in case 1 将某型舰船简化为等截面船体梁,基于Abaqus 软件建立了水下非接触爆炸作用下船体梁总体响应特性数值计算方法,利用缩比船体梁模型试验,验证了方法的有效性,对船体梁总体响应特性进行分析研究,得出如下主要结论: (1) 在不同爆炸工况下,所建立的数值计算方法能合理表征船体梁总体响应过程,预测船体梁的总体响应周期和响应幅值,其中响应周期的误差不超过6%,说明该研究方法较准确可靠,可为研究船体梁总体响应特性提供参考; (2) 在气泡脉动频率接近船体梁一阶湿频率(fb/fB接近1)的条件下,随着爆径比R/r减小,船体梁总体响应模式由鞭状响应进入中垂损伤,且在1 (3) 对于船体梁总体响应,随着水下爆炸工况增强,船体梁由全弹性响应逐渐进入弹塑性、塑性响应。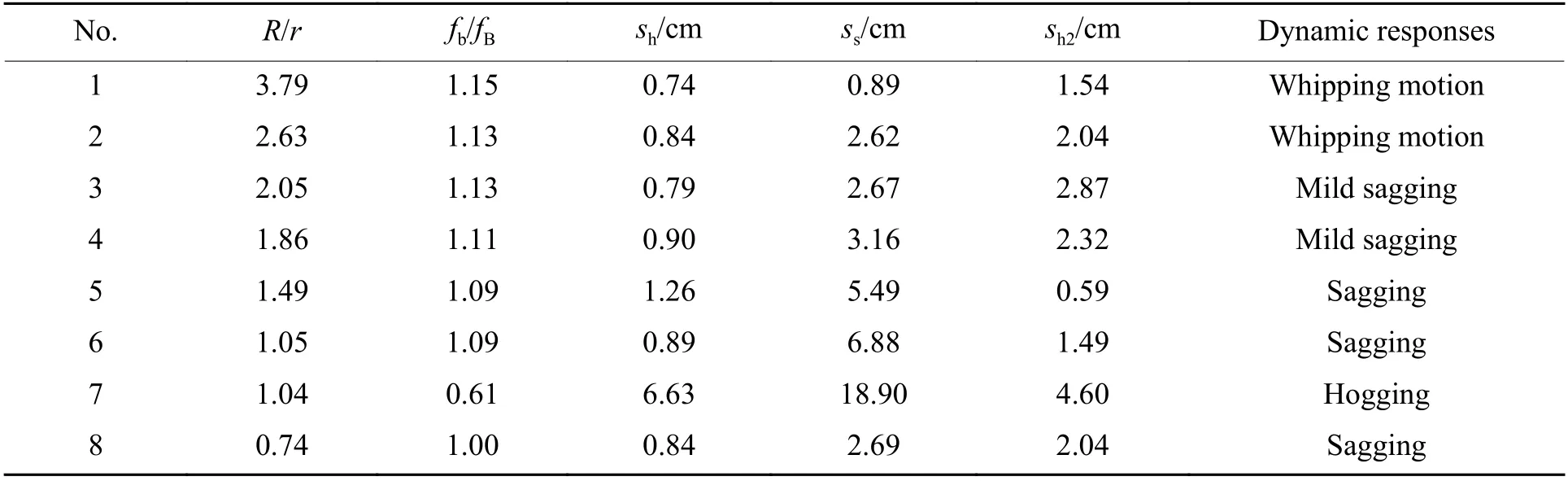
5.2 应变分析
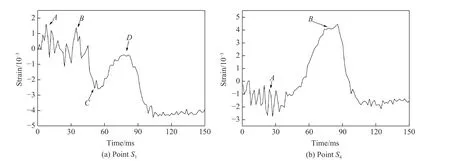


5.3 加速度分析
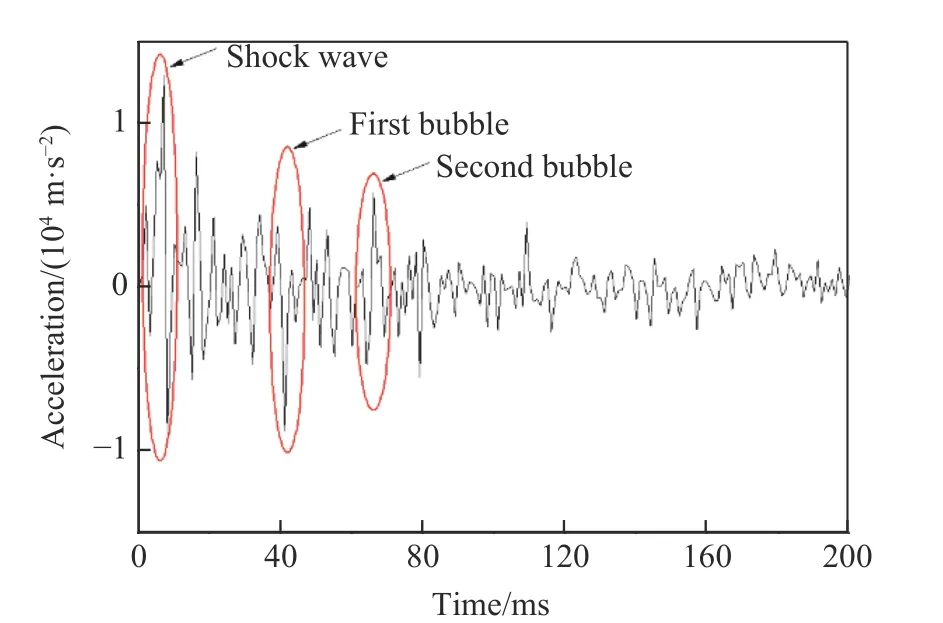
6 结 论
