基于形态学-HHT算法的船载地磁三分量信号分析与预处理
2021-12-03刁云云高金耀吴国超蔡晓仙
刁云云,高金耀*,吴国超,蔡晓仙,岳 梅
(1.自然资源部 第二海洋研究所,浙江 杭州 310012;2.自然资源部 海底科学重点实验室,浙江 杭州 310012;3.浙江大学 海洋学院,浙江 杭州 310058)
0 引言
地磁场是一种基本的地球物理场,通过X、Y、Z三个方向分量可反映其空间分布特征[1],时间上基本稳定,变化频率接近0 hz。拖曳式地磁测量是海洋磁力信息采集的主要手段,但在南、北极地磁的测量中,受限于水深环境、浮冰、作业效率等因素,通常采用航空或船载地磁三分量系统(STCM)测量。STCM为日本在1972—1975年间开发,已在多个海区采集了矢量地磁数据,精度为50±25 nT[2-7],测得的地磁信号包含真实地磁场、感应磁场、固有磁场、涡流场以及随机磁场,其中随机磁场来自磁力仪的测量噪声、船载电气设备的高频电子干扰、海底沉船、水面船只等铁磁性物质的短时强干扰[8]以及船体转向的脉冲干扰等。
滤波处理是消除随机磁场信号的重要手段。传统的滤波方法是对信号进行快速傅里叶变换(Fast Fourier Transform,FFT)获得频谱图,设置截止频率进行去噪处理获得目标信号。但对于频率复杂、随时间非线性、非平稳变化的极地地磁信号,该方法不适用。形态学滤波是基于数学形态学理论发展起来的一种针对非线性、非稳定变化信号的处理方法[9],可用于地球物理信号在时域上的信噪分离。如陈辉 等[10]用该方法对地震信号进行去噪,获得了较高信噪比的地震剖面信息。希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是近年发展起来的一种新的信号处理方法[11-16],与FFT相比,HHT具有保留原信号频率的优势[17]。BATTISTA et al[12]研究表明,针对电气设备的杂散场对地磁的干扰,HHT去噪效果较好;ZHOU et al[18]改进了HHT算法,通过引入差分磁场,增强了HHT的噪声识别能力和去噪效果;QIAO et al[19]优化了HHT算法中EMD分解算法;李季 等[8]发现HHT与形态学滤波结合可以有效降低模拟信号中随机噪声的干扰。总体上,对于实测地磁信号分析和处理的相关研究尚处于探索阶段。本文构建了一种形态学滤波和HHT变换相结合的滤波处理方法,对实测船载地磁三分量信号进行去噪和分析。
1 数据和方法
1.1 数据来源
第29次南极科考在普里兹湾海域同步采集了 2 443 km 船载地磁三分量和拖曳地磁总场数据,本研究分析的P6-2测线全长约187 km,呈南北向分布,采样时间约2.5 h。船载地磁三分量由Grad-03-500M三轴磁力梯度仪采集,仪器相关参数如表1所示。拖曳地磁总场由G880型标量地磁传感器采集,两者采集时间同步。P6-2测线数据见图1。

图1 第29次南极科考船载地磁三分量测线数据Fig.1 Three-component geomagnetic line data of the 29th Antarctic Scientific Expedition
三轴磁力梯度仪安装在船尾部风廓仪平台的桅杆上,平台距二层甲板15 m高,X分量和船艏向一致,Y分量指向右舷,Z分量垂直向下。姿态仪传感器用于采集船的姿态,与三轴磁力梯度仪相距约 10 m,两者同步变化。
本文以总场数据为例展示信号分析过程,总场的磁场值为50 000~51 500 nT,依据下式计算得到:
(1)
式中:X、Y、Z分别代表船载地磁测量的东向、北向、垂直地心三个方向的地磁分量,单位:nT;M代表地磁总场,单位:nT。
1.2 形态学滤波
采用形态学滤波分离船载地磁三分量中的脉冲信号。结构元素的选取是形态学滤波一个重要因素,其幅值一般应大于噪声幅值,小于信号主要轮廓高度的1%。参考陈辉 等[10]和柏林 等[20]设计的开-闭和闭-开组合滤波器,其中开运算可以压制峰值处的脉冲,闭运算能过滤低谷的脉冲干扰,组合滤波器公式为
y(n)={OC[f(n)+COf(n)]}/2
(2)
式中:OC表示开-闭运算,CO表示闭-开运算,f(n)代表原始信号,y(n)表示形态学滤波结果。
1.3 希尔伯特-黄变换(HHT)
HHT包括经验模态分解(EMD)和Hilbert变换两部分。EMD将非线性、非平稳的地磁信号自适应地分解为若干个线性、稳定、固有模态函数(IMF)。EMD分解判定条件有两个:(1)给定信号中,过零点数量和极值点数量相同或者相差1个;(2)在给定信号中,上下包络线的均值为零,具体计算方法可参考文献[8]和[12] 。IMF阶次越大代表地磁信号中低频、稳定成分越多;相反,IMF阶次越小代表中、高频成分占主要部分。
利用Hilbert变换计算各IMF分量的Hilbert谱,得到各信噪频段的分布。
EMD分解的地磁信号,通过Hilbert变换[21]获得时频分析,公式为
(3)

根据式(3)可进一步得到:
(4)
(5)
式中:ai为瞬时振幅;φi为瞬时相位;fi为瞬时频率,单位:Hz。
对各IMF含噪信号进行自相关分析,公式为
(6)
式中:E为数学期望,σ为标准差。
理想的白噪声在t2=t1时,R(τ)=1,其他位置为0。地磁信号的高频IMF分量以噪声成分居多,其自相关函数表现为以零点为中心,向两侧衰减为0;低频IMF分量以真实地磁信号为主,零点位置附近衰减缓慢[22]。
1.4 滤波效果检验
对形态学-HHT滤波和FFT滤波后的地磁总场进行滤波效果真实性检验。分别对两种滤波后的总场数据进行船磁校正计算,以拖曳地磁总场为基准计算均方根误差(RMSE),公式如下
(7)
式中:n代表数据个数,Mcal,i代表船磁校正后的地磁总场,Mty,i代表拖曳地磁总场。
2 结果和分析
2.1 形态学滤波
结合图1总场中脉冲信号的幅值和宽度情况,选取了三角结构元素为:[0,50,100,200,100,50,0],并采用式(2)的组合滤波方式,其计算结果如图2所示。
与原始地磁总场(图1a)相比,形态学滤波后的地磁总场(图2)滤除了大部分的脉冲点(在0 s和7 000~9 000 s之间达到51 000 nT以上的点),同时保留了真实地磁信号(50 000~51 000 nT),表明形态学滤波对船载地磁三分量数据有良好的去噪能力。
2.2 EMD分解结果
将形态学滤波处理后的总场数据(图2)经EMD分解成11阶次IMF分量和一个残余分量(图3),IMF1~IMF6在整个时间序列上幅值较均匀,且主要集中在±100 nT以内,推断集中了大量高频交变磁场噪声。IMF7~IMF11分量幅值变化平缓,代表了总场信号的低频成分,而残余分量幅值在50 000 nT左右,为总场信号的主要成分。

图2 总场形态学滤波结果Fig.2 The total field result after morphology filtering

图3 EMD分解结果Fig.3 Decomposition of total field signal by EMD
图4展示了IMF各分量自相关结果,在零时刻,IMF1~IMF5各分量幅值达到最大,自相关程度最大,但在偏离零时刻的其他时间段,幅值急剧衰减到0值附近,表明这些分量的自相关程度小,说明这些分量是由噪声主导的;偏离零时刻的IMF6~IMF11分量幅值变化缓慢(越低频的分量,幅值变化越平缓),且大部分不接近0,自相关程度高,表明IMF6~IMF11分量由地磁信号主导。

图4 IMF各分量自相关函数Fig.4 Autocorrelation function of each IMF
2.3 希尔伯特谱分析
IMF1~IMF6分量的希尔伯特谱如图5所示,IMF1~IMF2、IMF3~IMF4以及IMF5分量对应的希尔伯特谱(图5 a~5c),其频率范围逐步变低,依次分别是:0.030~0.460 Hz、0.010~0.100 Hz、0.005~0.030 Hz。IMF6分量信号频率整体接近0 Hz,但仍含有和0 Hz接近的噪声成分,从IMF7开始,信号都为0 Hz (图略),说明从IMF6分量开始,信号由相对稳定的地磁场构成。图5e为地磁总场的希尔伯特谱分布,在整个时间段,噪声和地磁场信号混叠在一起。
希尔伯特谱表明,主要地磁信号在0.030 Hz以下(图5a中红色直线),噪声范围为0.010~0.500 Hz(图5a~5c)。由原始三分量的总场计算的傅里叶谱(图5f)可知,信号频率在0~0.500 Hz之间,频带范围较宽,与希尔伯特谱相比,傅里叶谱无法得知各频率所对应的采样时间。
2.4 形态学-HHT滤波后的地磁总场
根据EMD分解结果和谱分析,对IMF1~IMF6分量分别采用巴特沃斯低通滤波[23],低通滤波设计参数为:通带最大衰减为3 db、阻带最大衰减为60 db、通带截止频率为0.01~0.03 Hz、阻带截止频率为0.10 Hz。
图6b中的绿色曲线代表形态学-HHT滤波预处理后重构的地磁总场图,包含了形态学滤波后经低通滤波的IMF1~IMF6分量和未滤波低频分量(IMF7~IMF11及残余分量)两个部分。与FFT滤波预处理相比,形态学-HHT滤波预处理后,数据整体较光滑,振荡程度较小,符合地磁场变化特性,大部分脉冲被有效压制,如0 s附近和7 000~9 000 s之间大于51 000 nT 的点(图1),高频噪声也被大幅削减。而图6a中的黑色曲线(FFT滤波后的地磁总场),虽然去掉了部分大于0.1 Hz的高频噪声(图5f)和脉冲信号,但仍含有较多低频噪声成分。

图5 各个IMF分量及总场信号频谱图Fig.5 Spectrum of each IMF and total field signal注:(a)代表IMF1和IMF2分量叠加的希尔伯特谱;(b)代表IMF3和IMF4分量叠加的希尔伯特谱;(c)和(d)分别为IMF5、IMF6对应的希尔伯特谱;(e)为总场信号的希尔伯特谱;(f)为总场信号的傅里叶谱。图a和b中红色细线指示分量信号最低频率界限。各分量图下方颜色条带代表振幅能量,单位:nT。Note:(a)represents the Hilbert spectrums overlying by IMF1 and IMF2 together;(b)represents the Hilbert spectrums overlying by IMF 3 and IMF 4 together;(c)and (d)are the Hilbert spectrums corresponding to IMF5 and IMF6 respectively;(e)are the Hilbert spectrums of all IMFs signal;(f)is the Fourier spectrum of total field signal by FFT.The red thin lines in fig.a and fig.b indicate the lowest frequency limit of the component signal.The color bars below graph represent the amplitude energy,unit:nT.

图6 两种滤波处理后的总场数据Fig.6 The total field signal data after filtering by two different methods
2.5 滤波效果的真实性检验
虽然形态学-HHT滤波压制了随机噪声的干扰,但与FFT滤波方法一样,滤波处理后的地磁信号中仍包含低频船磁的影响。图7为对2种滤波处理后的地磁信号进行船磁校正后的地磁总场结果。船磁校正后,形态学-HHT滤波的地磁信号整体起伏平缓,仅在局部存在“震荡”现象,除初始阶段(0~200 s)与拖曳地磁总场相差较大外,其他时段两者起伏趋势一致。而FFT滤波后的地磁总场信号整体震荡大,与拖曳地磁总场存在较大差距。分别计算船磁校正后2种滤波方法的地磁总场与拖曳地磁总场的均方根误差(RMSE),形态学-HHT滤波的RMSE约为194 nT,FFT滤波的RMSE约为600 nT,相差近3倍。
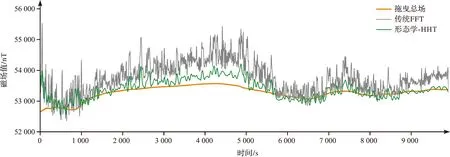
图7 两种滤波处理后的船磁补偿结果对比Fig.7 The comparison of ship magnetic compensation by two different filtering methods
总体上,与FFT滤波相比,形态学-HHT滤波处理后地磁信号形态和幅值变化更接近拖曳地磁总场,误差值更小,更适合用于船载三分量地磁数据的预处理。值得注意的是,船磁校正效果除了与预处理方法有关外,还与船磁校正算法、数据质量等息息相关。
3 结论
船载三分量地磁信号中包含了除船磁外的大量随机噪声干扰,形态学-HHT方法能够在时间尺度有效识别信号的频谱成分,自适应地进行信号分解,降低工作量,提高谱分析有效性,解决脉冲噪声干扰,对非平稳、非线性的船载地磁信号噪声压制优于FFT滤波算法,通过与拖曳地磁总场测量结果的比较也证明了该滤波方法的有效性。
