射电望远镜多目标观测策略优化*

2021-12-03翟楠楠刘志勇朱春花

天文学报 2021年6期

翟楠楠刘志勇王娜† 朱春花

(1新疆大学物理科学与技术学院乌鲁木齐830046)

(2中国科学院新疆天文台乌鲁木齐830011)

1 引言

天文望远镜在天文学的发展过程中起着至关重要的作用，随着天文学的发展对观测需求的不断提升，望远镜资源日益紧缺.如何利用稀缺的望远镜资源，进行合理的调度是提高望远镜有效运行时间的重要保障.望远镜调度问题是资源调度在天文观测领域的应用，该问题通常被转化为约束满足问题进行讨论，即在满足预定约束的情况下，尽可能提高目标函数的最优值[1].望远镜调度的目标函数旨在有限的资源内尽可能提高观测时间的利用率，提升观测数据的质量，实现观测效益的最大化.

针对该问题国内外学者已进行相关研究，例如Johnston等[2-4]考虑HST(Hubble Space Telescope)的运行环境、调度周期和调度程度，使用神经网络优化算法进行HST调度优化，构建SPIKE(Science Planning Interactive Knowledge Environment)通用调度系统框架，并成功应用于VLT(Very Large Telescope)、Subaru望远镜等[5].2012年Colome等[6]回顾前人对望远镜观测调度问题的研究，统计并比较各望远镜在该问题上使用的调度技术.2016年Solar等[7]使用混合整数线性规划优化算法，根据动态约束条件完成ALMA(Atacama Large Millmeter/Submeter Array)观测调度的研究.2018年Luo等[8]针对FAST(Five-hundred-meter Aperture Spherical radio Telescope)望远镜将调度问题建模为最小成本最大流问题来对申请观测项目进行调度，增加了观测项目的数量和总体的优先级，同时还减少望远镜换源成本.2019年Bellm等[9]针对ZTF(Zwicky Transient Facility)的科学观测需求使用整数规划的优化算法，完成了整晚的观测调度.以上调度方法均将观测周期分割成相同大小的时间片，将观测项目分割成多个调度块，通过计算各调度块在时间片上的适应值，选择项目最佳执行的时间片进行全局调度.这种方法对于换源过程少、单个目标观测时间长的观测项目来说能够快速处理并给出合理调度结果，然而对于单个观测时长较短、换源频繁的观测项目来说，观测过程中换源时长将占较大部分的时间，因此需要进行相应的讨论.

脉冲星到达时间观测，可以在较短的积分时间内获取有效的观测数据，是该类问题中的典型.当给定几百个脉冲星进行观测时，在观测过程中望远镜将会进行频繁的换源操作.2009年Balser等[10]考虑到GBT(Green Bank Telescope)在不同观测频率，天气变化因素对观测的影响程度，并针对该情况采用动态调度方式，对观测源列表进行实时规划，在环境变化时能够及时响应并调整观测计划.2018年Moser等[11]考虑到脉冲星的随机闪烁因素，将问题定义为具有不确定性的最短路径问题，使用两观测源间的角距离大小表示换源过程时间的消耗，并使用Parkes望远镜进行模拟，结果显示随机闪烁明显延长观测的时间，且不同的起始时间对观测结果有一定的影响.以上两项研究考虑到不确定因素的影响，通过预设信噪比阈值来确定观测数据的有效性，没有明确的初始观测积分时长.

综上所述，望远镜调度优化必然依赖其运行的具体状况、观测项目[12-14]，国内外学者研究工作均针对确定的观测模式和观测设备进行讨论.本文根据中国科学院新疆天文台南山26 m望远镜(下文简称南山26 m)脉冲星观测和观测源列表，对射电望远镜多目标观测问题进行初步探索.由于天体的周日运动，两个观测源间的角距离在地平坐标系下的投影随时间变化，即望远镜在两观测源间的转动时长随时间变化.图1给出了从同一个观测源J1825+0004在不同时刻转动到其他观测源的时长随时间的变化，其中UTC(Coordinated Universal Time)为协调世界时，图例的数值表示两观测源间的角距离.因此，对于该问题在有限时间内无法获取一个全局的最优解，采用贪心算法仅考虑局部优化，每次都选取当前状态下的最佳观测源.

图1 J1825+0004在不同时刻转至其他观测源的转动时长Fig.1 The slew time from J1825+0004 to other targets at different start times

2 数学建模

2.1 问题描述

脉冲星到达时间观测项目，由项目负责人给定包含n个脉冲星的集合T={T1，T2，T3，···，Tn}，初始时每个脉冲星源无优先级.由于各脉冲星源的流量密度不同，因此相对的观测积分时长也不同，在完成脉冲星观测后，再将望远镜偏移至目标背景进行跟踪定标观测，用于脉冲星流量及偏振标定.南山26 m的脉冲星到达时间观测频段为L波段，在该波段天气的变化对观测结果无明显影响，可以全天进行观测.在观测过程中由于望远镜电缆长度限制，因此望远镜无法按某一方向无限转动，当观测过程中触限位时望远镜将回转一周，设回转一周的时长为C.已知射电望远镜的地理坐标、各脉冲星的观测积分时长、项目起始时间ST(Start Time)和结束时间ET(End Time)，在时间段[ST，ET]内尽可能多地完成观测，提高观测时间利用率，最小化观测过程中换源时间的消耗.由于望远镜系统灵敏度与望远镜增益G成正比、观测总积分时长ObsDuration的平方根成反比，因此为保证观测数据的质量，应尽量在望远镜高增益的情况下进行观测，否则同等信噪比的观测将增加观测积分时长.南山26 m的脉冲星到达时间观测项目的观测过程如下所示:

(1)输入待观测列表集合、项目起始和结束时间、望远镜起始状态;

(2)按给定的顺序依次观测列表中的源;

(3)若当前源可以完整观测，则执行观测，并进行后续的跟踪定标观测;

(4)在观测过程中若电缆转动触限位，望远镜回转一周;

(5)该源观测完成后将该源从待观测列表中剔除，更新望远镜状态、时间等信息;

(6)若当前源不可完整观测，则跳过该源，依次选择下一颗源;

(7)若当前无可观测的源，则选择等待时长最短的源作为下一个观测源;

(8)重复步骤(3)-(7)直到项目申请时长耗尽或无源可观测结束.

2.2 参数定义

由于脉冲星的赤道坐标相对稳定，当已知第i个脉冲星Ti的赤经RAi、赤纬Deci，观测积分时长ObsDurationi，望远镜地理纬度Lat以及该源在地平坐标系下的最低可观测高度角度限制Ellim，则从赤道坐标系转为地平坐标系的公式为

其中Dec表示脉冲星的赤纬.通过该式可以计算望远镜纬度为Lat，脉冲星高度角为Ellim时，脉冲星所对应的时角HA.HA与RA和当地恒星时(Local Sidereal Time，LST)的关系为

通过该式可求时角所对应的当地恒星时LST.若时角HA=a，a值为正表示目标源在a时前经过本地子午圈，反之表示还需a时过本地子午圈.脉冲星升起时刻r，下落时刻s，分别为

通过(3)式还可计算出脉冲星Ti的可观测当地恒星时窗口TimeWini=[ri，si]，i代表第i个脉冲星.

在观测过程中望远镜的状态TeleState使用方位角、高度角、电缆缠绕角度3个参数表示，由于望远镜存在限位问题，因此在计算望远镜的转动角度时需要同时考虑最小转动角度、电缆触限位两个因素.为方便望远镜转动时长的计算，将望远镜的转动过程简化为角加速、减速度相同的匀变速转动模型.由于地平式望远镜在换源时需方位轴和俯仰轴共同转动，因此望远镜从当前位置转动到下一个源位置的转动时长取两轴上最长耗时.设Ti源上升至可观测高度角所需的等待时长为WaitTimei，望远镜从当前位置到Ti源处的转动时长为SlewTimei，若WaitTimei为较长时间段，可利用该段时间进行其他的工作，在该情况下两者不共用时间需独立计算.因此Ti源的观测起始时间为

若观测转动过程中的触限位状态记为RCi，此时Ti源的观测结束时间为

2.3 约束条件

根据上述分析，对脉冲星到达时间观测项目的调度问题建立以下约束:

(1)该项目中短期内的重复观测不会增加科学收益，所以每个源最多规划一次，并保存在已规划列表SchList中，若最多规划m个源，即:

(2)项目的观测时间必须在申请的观测时间段区间[ST，ET]内，即:

(3)脉冲星的执行观测时间必须在其可观测时间窗内，即:

(4)若望远镜在观测Ti源的过程中电缆缠绕角度TeleRi超过了可转动限位Rotationlim，则望远镜回转一周，即:

2.4 目标函数

规划过程中通过减少转动时长和等待时长，以提高望远镜观测的时间利用率，当WaitTimei是大块连续时间时可以进行其他的短周期科学项目或日常检测等工作，此类时长总和记为WaitTimeU，则相应的目标函数时间利用率记为f1:

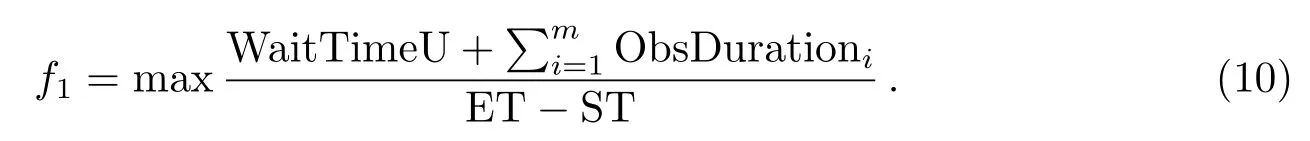
由于每个脉冲星的总观测积分时长已给出，因此为更好地提高观测数据质量，在观测过程中应保持脉冲源的观测高度角处于望远镜最佳增益所对应的高度角附近，假设Ti观测源的最佳观测高度角为BestEli，观测高度角为Alti，当脉冲星的最大高度角小于BestEli时，BestEli为脉冲星的最大高度角，否则BestEli为望远镜的最佳观测高度角.因此在观测过程中应保持距最佳观测角差值的平均值为最小，则相应的目标函数记为f2:

2.5 算法步骤

根据上述目标函数定义，首先将望远镜当前信息分别计算转动至可观测源处的转动时长矩阵S以及相应的与BestEli差值的平均值矩阵E进行归一化处理:

其中x表示同组数据中的一个数值，xmin表示同组数据中的最小值，xmax表示同组数据中的最大值.然后通过加权求和的方法同时考虑两个影响因素:

其中权重系数w1+w2=1.权重系数值越大表示对相应的因素偏好型越强，求得源的优先级矩阵P，其中值越小则优先级越高，越容易被选作为下一个观测源，具体步骤如图2所示.

图2 观测规划算法流程图Fig.2 Flow chart of observation scheduling algorithm

对于传统的人工规划工作，通常由经验丰富的天文观测人员进行.首先观测人员根据项目的起始时间估算对应的恒星时，由于低赤纬的观测源其可观测时间窗较短，因此根据(2)式中恒星时与赤经的关系，选择在起始时间可观测的低赤纬源作为起始源.然后遵循以下规则选择下一个观测源:(1)对于同赤纬源优先选择赤经大于当前源的观测源;(2)对于同赤经源优先选择当前可进行观测的低赤纬观测源.最后将剩余的观测源按其赤经和赤纬情况插入到前一步安排好的观测列表中.需注意由于个人的经验不同，因此人工规划的步骤存在差异.

3 实例分析

3.1 实例数据

为验证该调度算法的性能，使用南山日常脉冲星到达时间观测项目的319颗脉冲星作为模拟观测源列表记为timing.csv，将南山26 m的配置信息作为观测设备的参数进行测试.timing.csv中脉冲星在赤经/赤纬上的分布情况见图3，与PSRCAT(Pulsar Catalogue)目录中脉冲星的分布相同，脉冲星集中分布在银盘上，且仅有少数源能全天观测;timing.scv中脉冲星的观测积分时长统计如图4所示，所有脉冲星的观测和跟踪定标观测总时长约为3 d.望远镜地理经度为87.17809°，纬度为43.47176°，海拔为2080 m，设望远镜在各方位上的最佳望远镜增益对应的高度角为45°，可接受的连续空闲时间为30 min，观测起始时间ST为2020-12-10 00:00:00(UTC)，对应当地恒星时为11h05m25.76s.

图3 319颗脉冲星赤经/赤纬的分布情况Fig.3 Distribution of RA/Dec of 319 pulsars

图4 319颗脉冲星观测积分时间统计Fig.4 The observational integral time statistics of 319 pulsars

3.2 结果与分析

为确定不同的权重系数给观测排序结果带来的影响，使用起始的UTC时间进行模拟，最终结果如图5所示，图中的横轴均为(13)式中转动时长权重系数w1的值，图中上面两幅图分别为目标函数f1和f2的模拟结果值，其中f1值越大表示时间利用越充分，f2值越小则观测数据质量越优.图中下图纵轴为平均转动时长，该值越小则望远镜换源消耗越少，综上所述在w1=0.6，w2=0.4时，在两个目标函数上和平均转动时长上表现最好，因此使用该组权重系数对问题做进一步的讨论.由于天体的周日运动，低赤纬的源在一段时间内会处地平线以下，为验证1 d内不同起始时间对观测列表的影响，以1 h为间隔，进行24次只改变起始时间的模拟观测.同时为显示贪心算法的最终结果，使用timing.csv分别进行随机、人工、贪心算法3种规划方法并进行模拟观测，进行周期分别为1 d、2 d、3 d的模拟，结果如图6、图7、图8所示.

图5 权重系数不同时的观测模拟结果Fig.5 The results of simulation with different weight factors

图6 不同起始时间为期1 d的模拟，绿线是贪心算法的结果，蓝线是人工规划的结果，红线是随机规划的结果.Fig.6 The simulations of different start time during one-day，results from the greedy algorithm，human op eration and random order are indicated by green，blue，and red lines，respectively.

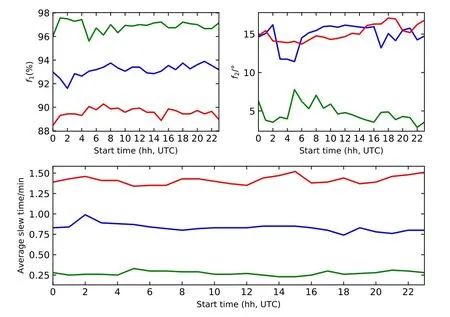
图7 不同起始时间为期2 d的模拟，绿线是贪心算法的结果，蓝线是人工规划的结果，红线是随机规划的结果.Fig.7 The simulations of different start time during two-days，results from the greedy algorithm，human op eration and random order are indicated by green，blue，and red lines，respectively.

图8 不同起始时间为期3 d的模拟，绿线是贪心算法的结果，蓝线是人工规划的结果，红线是随机规划的结果.Fig.8 The simulations of different start time during three-days，results from the greedy algorithm，human operation and random order are indicated by green，blue，and red lines，resp ectively.

由图6、图7、图8可以看出，目标函数f1上的结果显示贪心算法大于人工、人工大于随机，贪心算法模拟结果的平均转动时长约为人工的3倍，随机的5倍，有明显提升且相对稳定;在目标函数f2上的结果显示，人工和随机观测结果相近，即在人工排序过程中科研人员对多目标的观测很难考虑到观测数据质量的问题，贪心算法可有效地提升观测数据的质量.在图6中拥有充足的源，按照观测步骤不存在等待时长，所以相应的时间消耗多为转动消耗，随着观测周期的加长，可选源逐渐减少，因此在图7、图8中出现无源可观测的等待时间消耗，但大于可接受时长内的等待时间将用来做其他安排，相应的时间利用率有所增加.

图9是以0时为起始时间，对3种方法产生的列表进行3 d观测的模拟结果，其中图(a)为随机规划生成列表的模拟、图(b)为人工规划生成列表的模拟、图(c)为贪心算法生成列表的模拟.由图可以更加清晰地看出人工列表对f2的提升不明显，而使用贪心算法生成列表的结果有明显提升，执行观测的时间更加集中且有序.

图9 观测周期为3 d的模拟:(a)是随机规划的模拟;(b)是人工规划的模拟;(c)贪心算法的模拟.图中横轴是UTC时间，纵轴是观测的高度角，绿线是最佳高度角，灰线是最低高度角，蓝线是脉冲星观测，红线是背景跟踪定标观测.Fig.9 The results of simulation with three-days，panels(a)，(b)，(c)indicate the results from random，human operation，greedy algorithm.In the f igure，the abscissa represents the UTC time，and the ordinate represents the elevation angle of observation.The dotted line represents elevation boundaries，green is best，grey is lowest.The short lines represent observation traces，blue is pulsar observations，red is the tracking calibration observations.