制动摩擦片的偏磨仿真分析与优化设计
2021-12-03袁二娜
袁二娜
上海汽车制动系统有限公司
0 前言
摩擦片是制动系统中执行制动和传动功能的重要部件。它利用与旋转盘表面的摩擦力来阻止车辆运动,吸收机械能并将之转化为热能,同时伴随表层材料的损耗。摩擦系数、耐磨损性和耐热性是摩擦片的三个重要指标,影响着摩擦片的功能使用寿命。统计表明,机械零件80%失效是磨损造成的,因此检测摩擦片的磨损显得尤为重要。由于制动钳几何模型和输入载荷的非对称,盘厚不均匀、车轮转动扭矩等因素,往往会出现摩擦片磨损不均的现象,即偏磨,从而降低了摩擦片的使用寿命。如果偏磨严重,将会导致多种不良问题,如制动力矩输出不均、制动不平稳、制动跑偏[1]、低鸣噪音[2],甚至影响驾驶员的驾乘感觉和制动安全等。因此研究摩擦片偏磨对于制动钳开发有着重要和积极的意义。
台架试验是检验制动偏磨最为常用和直接的方法。它是按行业或客户标准,由制动器供应商进行试验验证,相对耗时费材,且拖延开发周期。随着有限元技术的发展,计算机仿真可以有效地弥补试验的不足,从而快速地复现和解决设计开发中的技术问题。本文依据实验标准建立某车型的制动系有限元模型,在Abaqus平台上依据Archard磨损理论进行程序开发,复现磨损,进行偏磨仿真分析。
1 磨损理论
相互接触运动的零件之间会产生摩擦,造成表层材料损耗和零件尺寸变化,这种现象可以用接触力学Archard磨损理论来解释[3]。它假设摩擦副的一方为较硬材料,另一方为较软材料。法向载荷W由n个半径为a的相同微凸体承受(如图1所示)。当材料产生塑性变形时,法向载荷W与较软材料的屈服极限σs的关系见式(1-1)。
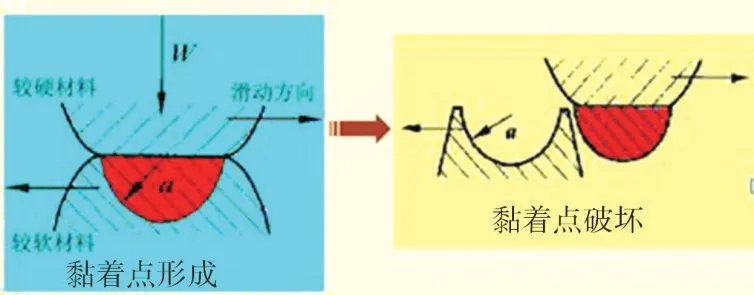
图1 Archard模型

当摩擦副产生相对滑动且每个微凸产生的磨屑为半球时,单位滑动距离的总磨损量Q0见式(1-2)。

如果考虑微凸体相互产生磨粒的概率数k和滑动距离L,则接触表面的磨损量Q为:

而对于弹性材料σs≈H/3,H是布氏硬度,则式(1-3)可修改为:

依据上述公式,在abaqus平台下进行节点磨损量计算程序开发,计算摩擦片的磨损量和偏磨。
2 有限元建模
为了准确模拟制动过程中摩擦片的行为状态,取制动钳总成、制动盘、羊角、摆臂作为几何输入条件(如图2所示)。网格划分的总原则是精少美悦,能用六面体网格的绝不用四面体网格,其目的在于确保网格质量和计算精度,并节省计算时间。对于几何不规则壳体、支架、羊角等铸造件采用四面体二阶单元划分网格,其它几何规则的零部件采用六面体协调单元。单元平均尺寸为4 mm,局部尺寸细化0.5~1 mm,总单元数21万。对于摩擦片与制动盘之间的接触建立采用点面接触,以便获取每个增量步的节点压力来计算磨损量和偏磨。其它接触对采用面面接触。

图2 制动钳有限元模型
3 偏磨仿真
3.1 测量点定义
在制动过程中,与制动盘接触的摩擦片表面都会受到不同程度的磨损。为了能全面反映摩擦片的磨损程度,同时考虑到后处理的可操作性,根据实验标准在摩擦片的内外圈上各选取4个点(如图3所示),每片共计8个点,以此8个点的磨损程度来反映摩擦片在径向和切向的偏磨,以及整体磨损程度。
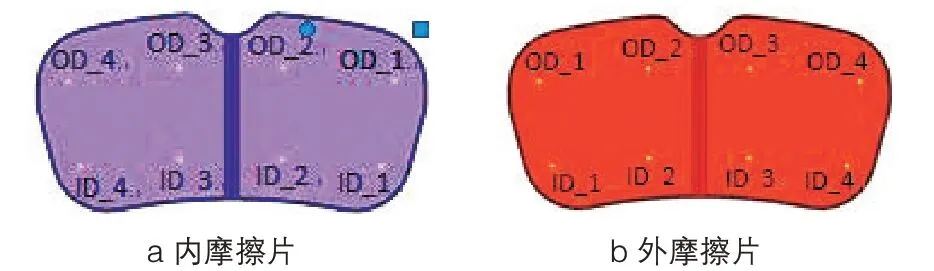
图3 摩擦片测试点布置
3.2 仿真结果
依据试验工况,选取22 bar和30 bar液压下的磨损数据,查看现有设计下摩擦片偏磨状况。表1和图4为内摩擦片偏磨数据。对内摩擦片而言,不同压力下磨损率和偏磨程度不同。首先压力越大切向和径向磨损斜率越大,即偏磨越严重。因此,高压制动更易导致偏磨问题。其次,当外半径leading侧的磨损量达到3.058 mm时,trailing侧的磨损量为2.837 mm,外半径的磨损率为3.24 um/mm;当内半径leading侧的磨损量达到3.024 mm时,trailing侧的磨损量为2.819 mm,外半径的磨损率为3.27 um/mm。因此,leading侧的磨损量要大于trailing侧,即偏磨发生在leading侧,此种现象与多数摩擦片工作中偏磨表现吻合。同时,对比内外径四对测量点的磨损可见,外径的磨损量大于内径的磨损量,因此径向主要是外侧偏磨。这也与摩擦片的实际工作表现吻合。

表1 内摩擦片磨损率
表2和图5为外摩擦片偏磨数据。对外摩擦片而言,压力也是影响偏磨的重要因素。对比22 bar和30 bar液压下的磨损率,可以看出压力越大偏磨越严重。其次,当外半径leading侧的磨损量达到2.96 mm时,trailing侧的磨损量为3.164 mm,外半径的磨损率为-2 um/mm;当内半径leading侧的磨损量达到2.959 mm时,trailing侧的磨损量为3.145 mm,内半径的磨损率为-2.97 um/mm;因此,trailing侧的磨损量要大于leading侧,即偏磨发生在trailing侧,恰与内摩擦片相反。而实际工作中,大部分外摩擦片的偏磨也都发生在trailing侧,这与制动钳自身结构和受力有密切的关系。同时,对比内外径四对测量点的磨损,可以看出,外径的磨损量略大于内径的磨损量,因此径向外侧偏磨,但没有内片严重。

图5 外摩擦片磨损曲线

表2 外摩擦片磨损率
由上述分析可定性得出,内片leading侧和外片trailing侧偏磨较重,主要表现在切向,需要结构优化以改善切向偏磨。

4 设计优化
4.1 优化方案
从Archard的磨损方程可知,压力和滑移速度是影响磨损的主要因素。径向和切向偏磨主要是因为压力分布不均和滑移线速度不同造成的,节点动态压力分布越均匀,偏磨越小。因此可以通过摩擦片开倒角,更改壳体、制动盘、活塞偏心、公差和尺寸配合、支架等结构[4]来改善压力分布。由于开倒角对噪音影响大,而其它零件基本冻结,不易更改,因此,从支架结构出发,通过加强支架桥部(如图6所示),希望改善偏磨,主要是切向偏磨。
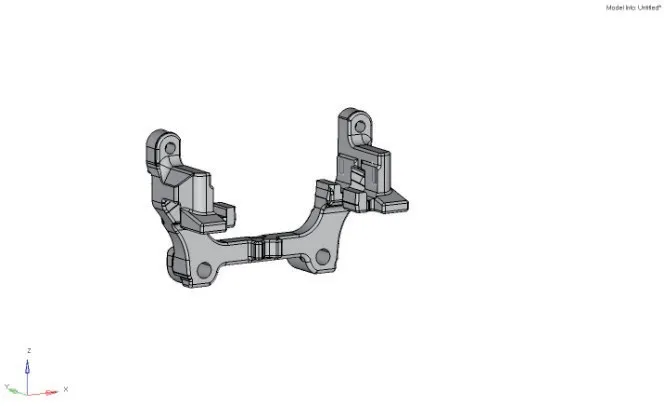
图6 加强后的支架模型
4.2 优化结果

图7内摩擦片磨损对比曲线
图7 和表3为支架更改前后内摩擦片偏磨数据。可以看出,在22 bar液压下,切向的平均偏磨由3.25 um/mm降到2.92 um/mm;在30 bar液压下,切向的平均偏磨由4.48 um/mm降到4.06 um/mm。由此可见,加强支架结构使切向偏磨得以改善,leading侧磨损得以减小。而对径向偏磨的影响甚微,且径向偏磨并不严重,可不予考虑。由此可见,加强支架结构也使外摩擦片切向偏磨得以改善。

表3 新旧方案内摩擦片磨损率对比
通过支架加强方案和仿真定性验证,可见内外摩擦片的偏磨都得到了改善,同时本方案也在台架试验中得以验证。
5 结论
本文根据制动钳的工作原理,建立了制动系有限元模型,并根据Archard磨损理论在Abaqus平台上实现了制动摩擦片偏磨模拟,很好地预测了偏磨趋势。通过更改支架结构使偏磨得以改善。因此,本仿真方法可作为研发中定性预测制动偏磨的
表4和图8为支架更改前后外摩擦片偏磨数据。可以看出,在22 bar液压下,切向的平均偏磨由2.98 um/mm降到2.60 um/mm;在30bar液压下,切向的平均偏磨由4.09 um/mm降到3.62 um/mm。一种快速有效的方法,同时本文所用的改善偏磨的方案也可作为实际工程项目的参考方案。由于本方法不能定量计算磨损,因此仅可以定性预测,还不能与台架试验形成定量对比。

表4 新旧方案外摩擦片磨损率对比
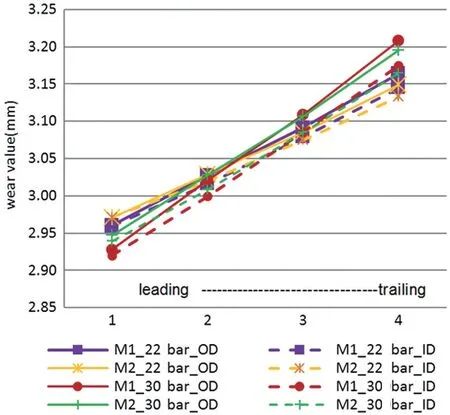
图8 外摩擦片磨损对比曲线
