人机交互力对下肢助力外骨骼关节期望角度的预测

宋纪元,朱爱斌,屠尧,武鑫雨,张育林,周旭

(1.西安交通大学机器人与智能系统研究所,710049,西安;2.西安交通大学陕西省智能机器人重点实验室,710049,西安;3.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安;4.中国煤炭科工集团太原研究院有限公司,030006,太原)

下肢外骨骼技术的开发是机器人技术和康复工程领域的进步[1]。识别穿戴者的运动意图以控制下肢外骨骼进行随动运动是该研究领域的重要问题,国内外学者从多方面进行了探究。

法国Wandercraft公司开发的Atalante机器人[2]可使用上身运动策略来检测下肢外骨骼的步态起始意图;Qiu等人采用人体动力学模型来估计人体步行意图[3];日本筑波大学研发的HAL外骨骼采用表面生物-电信号(EMG,electromyography)传感器、角度传感器、姿态传感器、足底压力传感器获取人体运动意图[4-5];神奈川理工学院研制的“动力辅助服”(PAS)[6]通过测量人体肌肉张力来获取人体感知;部分康复外骨骼,如MINDWALKER[7]、ReWalk[8]、Ekso[9]等,采用有限状态机加预定义曲线控制的方式,使用手表和控制按钮的运动模式切换;UC Berkeley大学研制的液压外骨骼BLEEX[10-12],采用灵敏度放大法进行外骨骼的实时跟随;中国科学院大学利用手臂的表面肌电信号区分七类运动,做为外骨骼机器人的控制指令[13];电子科技大学的陈启明等使用足底压力鞋的零力矩点ZMP作为特征信息,在外骨骼系统中学习并预测人体行走、停止的运动意图[14];西安交通大学的陈江城和李瀚哲等,采用训练神经网络模型拟合人体关节角度或关节力矩与EMG信号特征的非线性关系,实现了对下肢连续运动角度的估计和下肢关节力矩的预测[15-16];文献[17]提出一种采用踝关节处人机位姿误差信息用于外骨骼摆动腿的控制方法。

在之前的工作中,本团队采用了陀螺仪和足底压力信号[18]以及自研究可穿戴肌电采集系统采集人体下肢表面肌电信号[19]对人体运动意图识别做出了相关研究。通常情况下,陀螺仪和足底压力采集到的运动信息滞后于人体的运动,适合人体运动状态识别;肌电信号虽然相对人体运动具有一定超前性,但信号测量过程中存在的不稳定性使得在实际应用过程中有一定的困难。

本文以团队先前的交互力控制研究[20]为基础,针对步态的摆动相外骨骼的随动运动,将人体运动意图产生的大腿和小腿腿部交互力转换为作用于髋和膝关节的主动关节力矩,分别采用S型曲线模型和导纳控制理论建立关节力矩与关节角速度之间的映射关系,即可按照人体运动意图得到预测的下一时刻目标关节角度。本文致力于提升外骨骼穿戴者的人机交互柔顺性。

1 下肢助力外骨骼系统设计

本文采用的下肢助力外骨骼样机方案如图1所示,该外骨骼系统的髋关节和膝关节由Maxon EC90电机串联谐波减速器驱动;踝关节为被动关节,存在圆周阵列的弹性元件。外骨骼的腰部、大腿部和小腿部的长度都可调节,以适应不同身高和体型的穿戴者。外骨骼的腰部和腿部与人体之间用绑具连接,大腿部和小腿部的绑具底座分别安装了交互力传感器,以获取穿戴者腿部和外骨骼腿部之间的交互力信息。外骨骼的大腿部和小腿部分别安装有陀螺仪,可以获取外骨骼腿部的运动信息。

图1 下肢助力外骨骼样机系统

2 人体下肢运动分析及重力补偿

人体穿戴下肢助力外骨骼的理想柔顺状态是在步态摆动相过程中人体腿部的重量由外骨骼补偿,外骨骼跟随人体腿部运动。

人体步态的摆动相足部不接触地面,可将摆动腿简化为一个以髋关节为固定支点的二杆模型,建立如图2所示的人体下肢坐标系。大腿偏离y轴的角度为θ1,大腿屈曲为正;小腿轴线偏离大腿轴线的角度为θ2,小腿屈曲为正;大腿的长度为L1,质量为m1,大腿重心位置与髋关节旋转中心距离为Lg1;小腿与足部的质量为m2,小腿重心位置与膝关节旋转中心距离为Lg2;人与外骨骼大腿腿部交互力为F1,与髋关节旋转中心距离为Lc1;人与外骨骼小腿腿部交互力为F2,与膝关节旋转中心距离为Lc2。根据拉格朗日方程建立下肢摆动相的动力学方程,令其加速度和速度为零,即可得到在任意角度静止状态下人体腿部重力在交互力传感器位置测量方向的分量。

图2 人体摆动腿的简化模型

2.1 运动学分析和动力学建模

在人体下肢坐标系中,单腿模型大腿质心坐标为

(1)

人体单腿模型小腿质心坐标为

(2)

则系统中大腿的动能为

(3)

小腿的动能为

(4)

小腿的速度等于x、y方向分速度的平方和

(5)

大腿的势能为

E1=-m1gyg1

(6)

小腿的势能为

E2=-m2gyg2

(7)

由此可以得到该二杆模型的拉格朗日函数为

L=T-E=(T1+T2)-(E1+E2)=

m2gL1cosθ1+m2gLg2cos(θ1-θ2)

(8)

求得大腿的动力学模型方程为

m2gLg2sin(θ1-θ2)-F1Lc1

(9)

小腿的动力学模型方程为

(10)

2.2 人体重力补偿项

(11)

由式(11)可直接测量得出人体大腿长度L1=380 mm,交互力传感器距离髋、膝关节的距离Lc1=260 mm和Lc2=260 mm;大腿和小腿相对地面坐标系的角度θ1和θ2由陀螺仪直接测量得到,则去除腿部重力分量后的大腿和小腿腿部交互力分别为

(12)

去除腿部交互力传感器测量值中腿部重力分量后,交互力的数值可以作为人体运动意图的表征。为了便于将重力补偿后的腿部交互力用于髋,膝关节的期望关节角度预测,可将腿部交互力转换为髋,膝关节的关节力矩。由图2可知,由腿部交互力产生的髋关节力矩和膝关节力矩分别为

(13)

大腿质量m1和Lg1、小腿质量m2和Lg2等参数可以通过国家标准GB/T 17245—2004定义的人体各段质量及质心位置回归方程初步估计得到。回归方程的输入参数为人体体质量值和身高值,具体形式如下

Y=B0+B1X1+B2X2

(14)

式中:X1为人体质量,kg;X2为人体身高,mm;Y代表各段的质量m1、m2或者Lg1、Lg2;B0、B1、B2为回归方程的系数,如表1所示。

表1 人体下肢各体段质量及质心沿腿部方向位置的方程

带入实验对象的体质量和身高,通过式(14)估算得到大腿的质量m1=9.847 kg,Lg1=267.03 mm;小腿的质量m2=4.016 kg,Lg2=224.72 mm。

3 人体摆动腿的髋膝关节角度预测

为了预测下肢助力外骨骼下一时刻的期望关节角度值,分别采用基于S曲线的映射模型和基于导纳控制的映射模型两种非线性映射的方法在外骨骼的关节角速度与重力补偿后腿部交互力产生的关节力矩之间建立映射关系。

3.1 基于S曲线映射的髋膝关节期望角度预测

S型速度曲线控制常用于电机的速度控制,是一种平滑、可靠的速度控制技术,其加速度的变化连续,可以有效削弱对系统的冲击和振动[21]。本节将关节角速度与重力补偿后腿部交互力矩之间这种非线性映射关系用S曲线描述,如图3a所示。

(a)S型曲线示意图

一个完整的S型曲线运行周期包括3个阶段:缓速变化段、高速变化段和平层段。本文选用的S型曲线为Logistic型,关节角速度与腿部关节交互力矩之间的映射关系,可以表达成如下公式

(15)

式中:ω为关节的角速度;τ为关节力矩;a、b、c为模型的参数。

如图3所示,改变式(15)的不同参数,可以改变S曲线3个阶段的曲线形态。参数a能调节输出关节角速度的最大值,参数b能调节关节角速度高速变化区的变化剧烈程度,参数c能调节重力补偿腿部产生的关节交互力矩的阈值大小。

对关节角速度积分后,即可预测期望的下一时刻k的关节角度位置

θk=θk-1+ωΔt

(16)

为了定义S曲线的合理参数,采用Vicon光学运动捕捉系统采集人体步态信息,对正常人行走过程中不同步频的步态曲线进行分析。如图4所示,正常人在相同步幅不同步频的行走过程中髋膝关节角度范围一致,髋关节角度范围约为-25°～15°,膝关节角度范围约为-15°～25°;髋关节角速度范围约为-150(°)/s～200(°)/s,膝关节角速度范围约为-200(°)/s～250(°)/s。为了适应更大步频和步幅的行走运动以及其他运动模式的需要,对关节角度和关节角速度的范围进行适当地扩大。选定髋关节角度范围为-35°～35°,角速度上限值为250(°)/s,髋关节伸展方向为正,屈曲方向为负;膝关节角度的范围为-10°～70°,角速度的上限值为250(°)/s,膝关节屈曲方向为正,伸展方向为负。

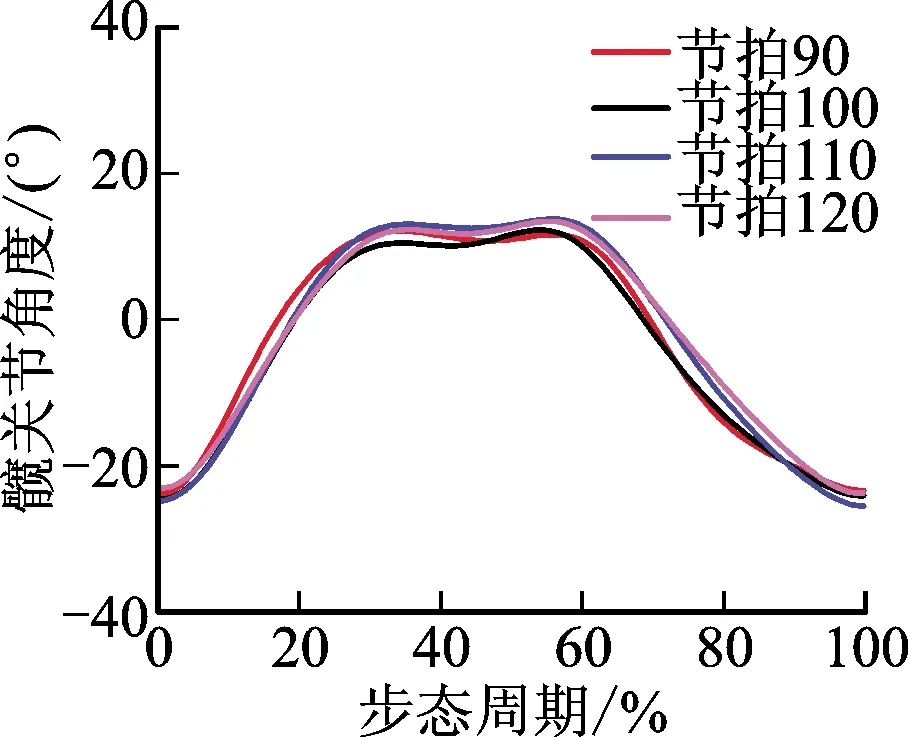
(a)髋关节角度曲线

为了确定人体穿戴外骨骼时合理的腿部交互力值范围,外骨骼机器人的腰部被固定在型材架上,实验对象穿戴下肢助力外骨骼单腿抬起并保持髋关节电机锁定不动,设定膝关节电机以0.5 Hz的频率来回摆动。分别在人体运动超前于外骨骼膝关节运动、人体运动滞后于外骨骼膝关节运动和人体运动跟随外骨骼膝关节运动3种运动过程中测量小腿腿部交互力,得到结果如图5所示。从图5a中可以看出,当人体运动超前于外骨骼膝关节电机运动时,腿部交互力值的范围为-40～20 N;从图5b中可以看出,当人体运动滞后于外骨骼膝关节电机运动时小腿交互力的范围为-50～10 N;从图5c中可以看出,即使人体有意识地跟随了外骨骼的运动,腿部交互力依旧有最大10 N的波动,这可能是高减速比的减速器造成的。因此为了消除由于腿部交互力变化造成的低速震荡,S曲线的参数c以10为初值,在后续的调试中向上递增进行参数调优。综合上面3种实验的结果,设定人体的腿部受力合理范围为-40～40 N,根据式(13)即可得出作为S曲线输入的关节力矩合理范围。

(a)超前运动小腿交互力

将测量得到的人体跟随外骨骼运动下的小腿腿部交互力值通过式(13)计算出主动力矩,作为S曲线式(15)的输入绘出腿部交互力产生的主动力矩与关节角速度之间的映射关系曲线。

当大多数的主动力矩值落在缓速变化区和平层区时,只有较少的点位于高速变化区。这样的映射关系明显是不可取的,因为这种映射关系会使得大部分的关节角速度在最大正向速度和最大反向速度之间变化,造成关节角加速度突变从而引起抖动的发生,这是不符合实际的外骨骼需求的。相反,如果使得尽可能多的主动力矩值位于S曲线的高速变化段,则外骨骼关节运动速度随人机交互力矩的改变能够均匀平滑地改变,能够表现出期望的柔顺性。改变S曲线式的参数值使得尽可能多的主动力矩值位于S曲线的高速变化区内,S曲线参数变化过程中主动力矩值与关节角速度的映射关系曲线如图6a所示,当参数a为250、b为0.3、c为500时,大多数主动力矩落在了缓速变化区和平层区,只有较少的点位于高速变化区;图6b和6c中,不断减小b的值,可以看出越来越多的主动力矩值进入高速变化区,映射关系也越来越合理,但当a为250、b为0.003、c为500时,缓速变化区消失了。这种映射关系会引起运动时的低速震荡和误触发,因此需要增大参数c,扩大缓速变化区的范围;如图6d所示,当a为250、b为0.003、c为2 000时,主动力矩值与关节角速度的映射关系曲线同时具有缓速变化区、高速变化区和平层区,该曲线平滑且较多的主动力矩值落在了高速变化区。

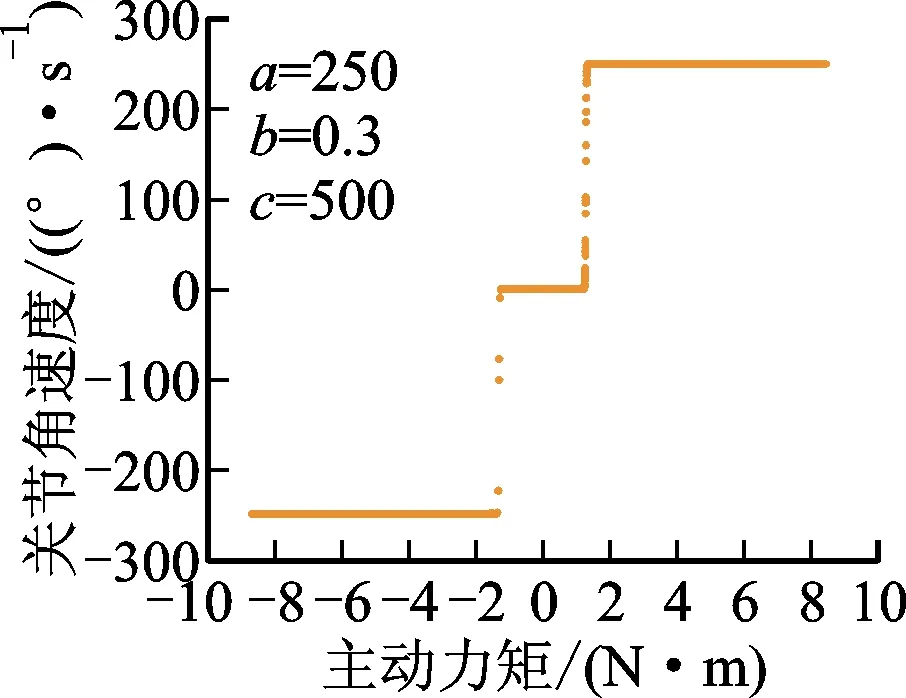
(a)b=0.3,c=500

3.2 基于导纳控制模型的髋膝关节期望角度预测

机器人的导纳控制方法是通过调节机器人末端位置与力之间的动态特性来实现柔顺性,能够把传统的位置控制和力控制统一到一个有机的整体中,其位置或者力的控制精度取决于控制参数与环境的阻抗特性[20]。本节将研究导纳控制模型用于建立下肢助力外骨骼的关节角速度与重力补偿后的腿部交互力对应的关节力矩之间的非线性映射关系。

3.2.1 导纳控制原理 根据导纳控制的基本原理,可将外骨骼和人体构成的动态系统简化为弹簧-质量-阻尼系统模型,如图7所示。

图7 导纳控制原理

构建导纳控制器的传递函数为

(17)

式中:ΔX为机器人的位置偏差值;ΔF为测量交互力与期望力的偏差值;Md为惯性系数;Bd为阻尼系数;Kd为弹性系数。

3.2.2 基于导纳模型预测期望关节角度 由于在人机物理交互牵引运动的过程中,外骨骼不需要具备回复力,则可将刚度参数Kd项忽略,对于输出速度的导纳控制器,式(17)可表示为

(18)

式中:ω(s)为外骨骼机器人关节运动角速度;τ(s)为经过重力补偿后腿部交互力对应的主动力矩。

如图8所示为依据导纳控制原理构建的机器人控制器框图。外骨骼通过腿部的力传感器采集人机交互力数据,经重力补偿后,根据式(13)计算腿部交互力产生的主动力矩。将主动力矩和外骨骼关节当前的位置、速度、加速度等运行参数作为导纳控制器的输入,经导纳控制器运算后输出机器人的目标运动角速度,最后将角速度乘以控制周期并加上当前的关节角度即可得到期望的关节角度。

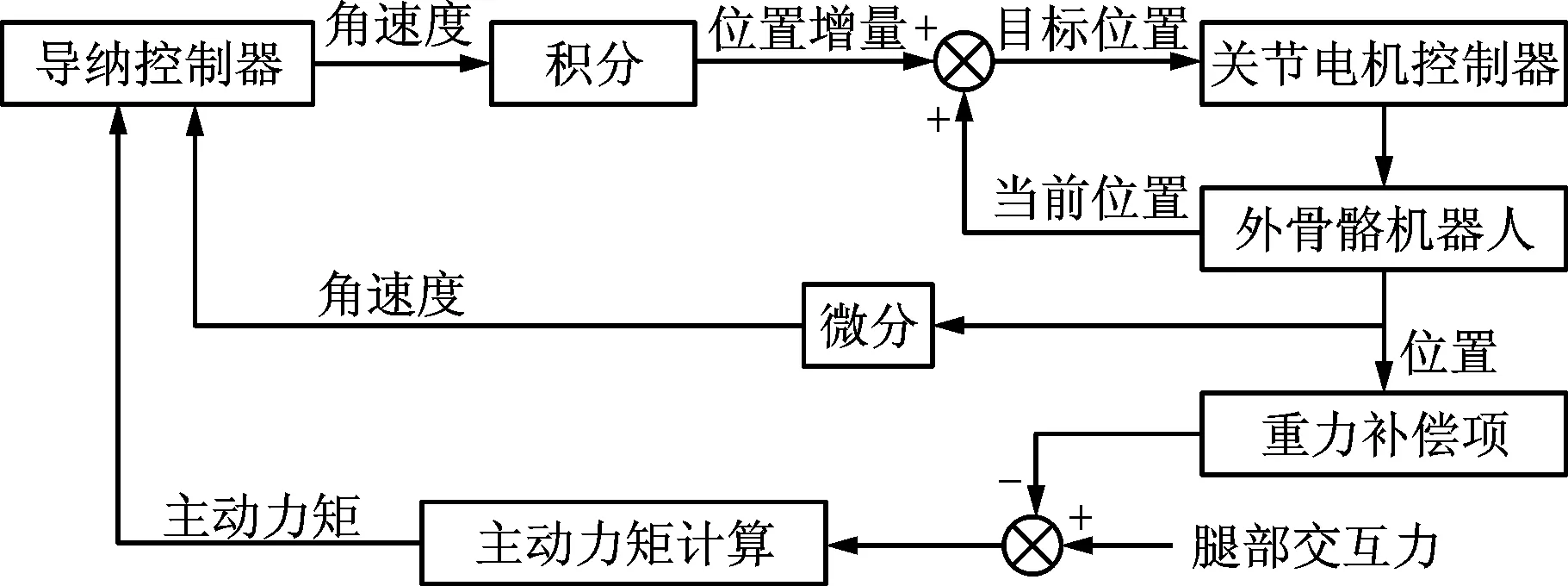
图8 机器人导纳控制器框图

在实际的外骨骼机器人运动控制过程中,需要对导纳控制器进行Tustin变换(即双线性变换),从而将导纳控制器的各输入输出量由连续信号转化为离散的数字信号,以便于进行编程控制。双线性变换公式为

(19)

式中:T为导纳控制器系统的控制周期。

将双线性变换式带入传递函数式(18)得到离散化后的导纳控制器为

(20)

通过z变换计算法则,可得到外骨骼机器人的关节角速度差分表达式为

(21)

同理,将角速度乘以控制周期再加上当前的关节角度即可得到期望的下一时刻关节角度位置

θk=θk-1+ωΔt

(22)

4 实验与结果分析

外骨骼腰部被固定在型材架上,分别进行基于S曲线映射和基于导纳控制模型的外骨骼主动控制实验,如图9所示。实验对象从腿部竖直状态先做髋关节的屈曲运动抬起大腿,随后连续做膝关节的伸展和屈曲运动,接着做髋关节的伸展运动,最后回到实验的初始位置。

(a)起始状态

4.1 基于S曲线映射的外骨骼摆动腿主动控制实验

基于S曲线映射的摆动腿主动控制实验中,当髋关节的S曲线参数a取250、b取0.003、c取2 500且膝关节的S曲线参数a取250、b取0.003、c取1 500时,外骨骼机器人启动平缓且保持在某一位置时无低速震荡现象,整个实验过程中外骨骼对人体的跟随运动柔顺流畅。

实验过程中大腿交互力的变化曲线如图10a所示,实验过程中小腿腿部交互力的变化曲线如图11a所示,经过滤波后的大腿交互力曲线较为平滑。外骨骼髋关节对人体运动的跟随过程中,人机间大腿交互力的最大值小于25 N。外骨骼膝关节在对人体运动跟随过程中,小腿交互力最大值小于20 N。外骨骼髋关节的角度变化曲线如图10b所示,膝关节的角度变化曲线如图11b所示,可以看出髋关节和膝关节电机角度曲线变化平滑,运动柔顺。

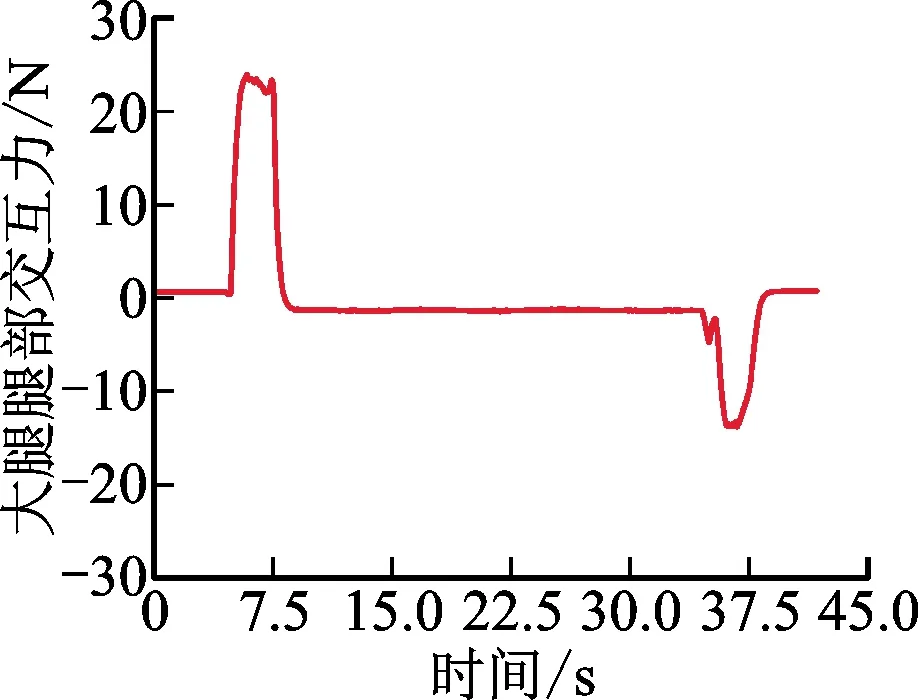
(a)大腿腿部交互力曲线

(a)小腿交互力曲线

4.2 基于导纳控制模型的外骨骼主动控制实验

外骨骼具有良好柔顺性的关键在于导纳控制器参数的合理选择,本部分通过多参数对照试验的方法,配置不同的惯性系数M与阻尼系数B,在小腿连续摆动下对腿部交互力数据对比。图12所示为固定导纳控制器惯性参数M、改变阻尼参数B的实验结果,可见随着阻尼参数B的增加腿部随动运动交互力的峰值也在逐步增加,但如果阻尼参数B过小,则容易出现关节的低速震荡现象。因此,导纳控制器阻尼参数B的选取方式是从较小值开始逐步增大。

(a)B=0

图13为固定导纳控制器阻尼参数B、改变惯性参数M的实验结果。可见,随着惯性参数的增加,腿部交互力的峰值也在逐步增加,但增加量稍小于阻尼参数。同样地,惯性参数M过小也会导致外骨骼低速震荡,因此导纳控制器的惯性参数M的选取方式是从较小值开始逐步增大,在外骨骼不出现低速震荡现象时的惯性参数M作为最优的参数值。

(a)M=1

根据以上研究最终选取的髋关节惯性参数M为10,阻尼参数B为2。如图14所示是大腿交互力曲线和髋关节角度曲线,从曲线可以看出在外骨骼跟随人体运动过程中,大腿腿部交互力的峰值小于10 N,相比于基于S曲线映射的控制算法,导纳控制模型对于人体运动意图的跟随性更好。

(a)大腿腿部交互力曲线

选取的膝关节惯性参数M为10,阻尼参数B为2,小腿交互力曲线和膝关节角度曲线如图15所示,可以看出在外骨骼跟随人体运动过程中,小腿腿部交互力的峰值小于15 N,相比于基于S曲线映射的控制算法,导纳控制模型对于人体运动意图的跟随性更好。与图5c中人体有意识地跟随外骨骼的运动,腿部交互力最大10 N的初始值对比,导纳控制模型实现了外骨骼的柔顺运动效果。

(a)小腿腿部交互力曲线

5 结 论

本文针对人体穿戴外骨骼单腿摆动相的外骨骼随动运动交互力过大的问题,为了将外骨骼与人体间的腿部交互力转化为人体髋膝关节下一时刻运动到的期望角度,实现对人体运动意图的识别,对关节角速度与腿部交互力产生的主动关节力矩间的映射关系进行研究。首先通过步态采集实验的关节角度数据,分析了正常人日常步态中下肢摆动相的运动特性,确定了人体不同相位采用的关节角度预测策略;然后将人体下肢摆动相的腿部简化为以髋关节为支点的平面二杆模型,建立人体下肢摆动腿动力学模型得到人体的重力补偿项;最后针对腿部摆动相,分别通过S曲线映射和导纳控制模型的方式,建立人体的关节角速度与重力补偿后腿部交互力产生的关节力矩之间的非线性映射关系,得到人体摆动相髋膝关节的期望角度预测公式。基于S曲线映射的期望角度预测算法使得外骨骼在摆动相跟随运动过程中大腿腿部交互力小于25 N、小腿腿部交互力小于20 N;基于导纳控制模型的期望角度预测算法使得外骨骼在摆动相跟随运动过程中大腿腿部交互力小于10 N、小腿腿部交互力小于15 N,且关节角度曲线平滑。导纳控制模型相比于S曲线映射算法能更好地识别人体运动意图。

同样地,当人体下肢腿部支撑地面运动时,则形成以踝关节为支点形成倒立摆,外骨骼的髋、膝关节也需随动运动。在接下来的工作中,我们需要做包括摆动相和支撑相的人体穿戴外骨骼在完整过程中的随动控制,进一步提升外骨骼在实际穿戴场景中的人机交互柔顺性和舒适性。