局部有源忆阻器电路及其在HR耦合神经元网络中的应用
2021-12-02乔印虎
孙 亮 罗 佳 乔印虎
①(池州职业技术学院机电与汽车系 池州 247000)
②(安徽科技学院机械工程学院 凤阳 233100)
1 引言
忆阻器被认为是继电阻、电容和电感之后的第4种基本电路元件,它表征了电荷与磁通之间的本构关系,具有纳米尺寸、非线性、低功耗和非易失性等特点。1971年,美国华裔科学家Chua教授[1]从数学对称性出发提出忆阻器理论并预测了它的存在性,2008年美国惠普实验室首次发现单个纳米级TiO2忆阻器件[2]。此后,许多不同的器件被确定为忆阻器,并提出了不同的应用,特别是忆阻器用于模拟生物突触[3-5]。
局部有源被认为是复杂性的起源,与生物神经突触具有密切联系[6,7]。2014年Chua教授[8]首次提出局部有源忆阻概念并设计了第1个局部有源忆阻器模型。2017年局部有源忆阻器被实验室证实[9]。局部有源忆阻器比无源忆阻器具有更加复杂的动力学特性,具有更加广泛的应用。近年来,一些局部有源忆阻器模型已经被提出和应用。例如,2018年Jin等人[10]提出一个局部有源忆阻器并与电容、电感电路组合实现了最简单的混沌电路。同年,Chang等人[11]实现了一种双稳态双局部有源忆阻器。2019年,Weiher等人[12]进一步从材料物理实验的角度证明了局部有源忆阻器的存在性。2020年,文献[13,14]首次把局部有源忆阻器引入人工神经元模型中,并提出了局部有源忆阻神经元模型。尽管一些局部有源忆阻器已经被报道,但是局部有源忆阻器因为数学模型复杂、有源区间小等缺点很难在人工神经网络中应用。生物神经系统具有丰富且复杂的放电活动,了解神经元以及神经元网络的放电动力学机制有助于人工智能的发展,在过去的几十年中已经吸引了大量的研究人员[15,16]。Hindmarsh-Rose (HR) 神经元具有简单的数学模型[17],能够模拟周期尖峰和簇发等多种神经元放电[18,19]。2019年Bao等人[20]使用一个无源忆阻器模拟两个HR神经元之间的连接突触,提出了基于忆阻突触耦合HR神经元网络,并分析了其同步动力学机制。
本文设计了一种简单的局部有源忆阻器模型,不仅数学表达式简单,物理电路实现容易,而且非常适合于模拟生物突触。使用该局部有源忆阻器模拟两个HR神经元之间的连接突触,构建了一种局部有源忆阻突触耦合的HR神经网络。这种局部有源忆阻突触耦合HR神经网络能够产生多种尖峰放电模式以及复杂的混沌行为。同时为了促进工程应用,设计了该局部有源忆阻器及其耦合神经网络的等效实现电路,并由电路仿真验证了数值仿真的正确性。
2 局部有源忆阻器
2.1 数学模型
根据忆阻器理论,一个广义的压控忆阻器可以表示为[21]

其中,W(x)是一个以x为变量的连续函数,称为忆导,v, i, x分别表示施加在忆阻器两端的输入电压,通过忆阻器的输出电流,和忆阻器的内部状态变量。基于式(1)和式(2),一个新的局部有源忆阻器模型能够被设计,它的表达式为

其中,x是忆阻器的内部状态变量,表示磁通,tanh(.)是双曲正切函数。
2.2 伏安特性
根据忆阻器理论[21,22],任意忆阻器应该具有以下3个特征:(1) 在双极性周期信号的驱动下,假设存在周期响应,该器件在电压-电流(v-i)平面中必须表现出过原点的收缩紧磁滞回线;(2) 从某个临界频率开始,紧磁滞回线波瓣面积应随着激励频率的增加而单调减小;(3) 当频率趋于无穷大时,收缩紧磁滞回线应收缩为单值函数。
当在局部有源忆阻器两端施加双极性周期激励信号v=Asin(2πFt)时,不同的激励信号幅度和频率对忆阻器的作用被研究。例如,当设置激励信号频率F=2,初始状态x(0)=0时,改变不同的信号幅度A所得到的伏安特性如图1(a)所示。从图1(a)可以看到,3个紧磁滞回线都通过v-i平面的0点,且幅度越大紧磁滞回线面积越大。当设置激励信号幅度A=2,初始状态x(0)=0时,调节不同的信号频率F所得到的伏安特性曲线如图1(b)所示。由图1(b)可见,3个紧磁滞回线都通过v-i平面的0点,且随着信号频率的增加,忆阻器的紧磁滞回线面积越来越小,逐渐趋向于一条直线。显然,所提忆阻器模型具有忆阻器的3个特征,是一种忆阻器件。

图1 输入信号幅度/频率相关的伏安特性曲线图
2.3 局部有源性
根据局部有源理论[8],如果一个忆阻器的直流(Direct Current, DC) 电压-电流V-I 曲线存在负的斜率部分,那么该忆阻器就是局部有源的。为了证明所提出的忆阻器是局部有源忆阻器,它的局部有源特性被分析如下:
首先令忆阻器状态方程dx/dt=0,可以得到它的平衡点状态方程

其中,V表示直流输入电压,X是满足dx/dt=0时的x的解。然后再把式(5)替换到式(3)中得到输出电流为

基于式(5)和式(6)可以得到忆阻器的DC V-I曲线,如图2所示。由图2可知,忆阻器的DC V-I曲线存在两个对称的负斜率区间,分别是0.89 图2 局部有源忆阻器的DC V-I图 基于式(3)、式(4)局部有源忆阻器模型,可以实现它的等效电路,如图3(a)所示。其中,U是模拟运算放大器,M是模拟乘法器。双曲正切函数使用文献[14]所提出的双曲正切电路实现,如图3(b)所示。在双曲正切电路中,当直流供电为±15 V,R=10 kΩ, RF=520 Ω, RC=1 kΩ, Io=1.1 mA时,电路能够实现vo=-tanh(vi)。忆阻器内部状态通过积分器的输出电压表示。根据基尔霍夫定律,局部有源忆阻器的电路方程可表示为 根据基尔霍夫定律,忆阻器数学模型式(3) i=x2v在忆阻器仿真器中对应的关系为i=(g2vz2v)/RL。其中,v和i分别表示输入电压和输出电流,g=1为模拟乘法器的增益,vz为积分器输出电压,表示忆阻器内部状态变量x,RL为可调匹配电阻。令R=10 kΩ, C=10 nF,根据积分时间常数RC=τ,可求得RL=g2R=1 0 k Ω, RA=R/0.5=2 0 k Ω,RB=R/1=10 kΩ。为了验证数值仿真,在功率模拟(Power SIMulation, PSIM)电路仿真软件中创建图3所示电路,如图4所示。为了方便测量忆阻器的输出电流,在仿真时把RL接地。 图3 电路图 图4 忆阻器PSIM仿真电路图 对于数值仿真输入电压源v=Asin(2πFt)所对应的电路实验输入电压源v=Asin(2πft),其中f=F/RC。因此,当数值仿真中F=2时,电路仿真频率f=20 kHz,不同的电压幅度仿真结果如图5(a)所示。当A=2时,不同的电压频率仿真结果如图5(b)所示。显然,图5的电路仿真结果与图1的数值仿真结果基本一致。 图5 局部有源忆阻器电路PSIM仿真结果 人类大脑包含了数以亿计的神经元,它们通过突触互相连接组成强大的神经网络。突触在神经网络中不仅是物理连接,而且对于神经元之间的电信号传输起着关键的作用。由于忆阻器具有类似突触的纳米级、可塑性、非线性和非易失性等特点,可以使用忆阻器模拟神经突触来开发等效的忆阻神经电路[23,24]。忆阻神经电路具有丰富的类脑放电动力学,利用忆阻器重构神经电路已经成为重要的研究课题。2维的HR神经元模型能产生丰富的尖峰和簇发放电行为,非常适合神经动力学的研究,其数学模型为[17] 其中,x是神经元的细胞膜电位,y是恢复变量,a,b, c, d是神经元模型参数。当使用局部有源忆阻器模拟两个HR神经元之间的神经突触时,两个神经元之间的膜电位差的改变将引起磁通的变化,从而产生电磁感应电流。此时,膜电位与突触的耦合可以使用忆阻器来描述[20]。因此,局部有源忆阻突触耦合HR神经元网络模型能够被建立,如图6所示。当两个HR神经元通过局部有源忆阻器耦合时,由于两个神经元之间的膜电位差x1-x2不断改变从而产生磁感应电流,感应电流可以通过忆阻器表征为ρ1(x1-x2)W。当这个磁感应电流分别作用在两个神经元上时,可以得到 图6 局部有源忆阻突触耦合神经元网络结构图 其中,ρ1, ρ2表示忆阻突触耦合强度,x1和x2分别表示神经元1和神经元2的膜电位,x1-x2表示两个神经元的膜电位差,y1和y2分别表示两个神经元的恢复电位,忆导W=z2表示突触权重,参数σ表示磁通泄露系数。 根据参考文献[13]的定义,神经放电模式一般可以分为周期的尖峰和簇发放电,随机的尖峰和簇发放电,混沌的尖峰和簇发放电以及混沌放电模式。当保持模型参数a=1, b=3, c=1, d=5, I1=-0.5, I2=-2.5, σ=0.2不变,两个不对称忆阻突触耦合参数ρ1,ρ2作为可调参数时,局部有源忆阻突触耦合HR神经元网络动力学行为被研究。设置ρ2为0.1,初值为(0.2, 0.2, 0.2, 0.2, 0.2),当忆阻突触耦合强度ρ1在区间[-1, 0]中逐渐增大时,系统的分岔图和相应的李雅普诺夫(Lyapunov)指数谱可绘制如图7所示。从分岔图中可以看到,系统随着耦合强度的增加,产生了多次正向周期倍分岔现象,在ρ1=-0.46时第1次由周期尖峰放电进入混沌放电后又多次以切分岔路径退出混沌再次通过周期倍分岔进入混沌状态。形成了多个不同周期放电的周期窗口。最后,在ρ1=-0.06时系统进入静默状态。图7(b)中李雅普诺夫指数谱验证了分岔图的正确性。图8给出了不同耦合强度ρ1时,系统的不同动力学行为时序图。从图8可见,局部有源忆阻突触耦合HR神经元网络能够产生周期-1尖峰放电、周期-2尖峰放电、随机尖峰放电、混沌簇发、混沌放电等多种放电模式。 图7 关于忆阻突触耦合强度ρ1动力学状态分布 图8 不同忆阻突触耦合强度ρ1所对应的多种放电模式 设置ρ1为-0.4,初值为(0.2, 0.2, 0.2, 0.2,0.2),当忆阻突触耦合强度ρ2在区间[0, 1]中逐渐增大时,系统的分岔图和相应的李雅普诺夫指数谱可绘制如图9所示。从图9(a)可以发现,在初始条件(0.2, 0.2, 0.2, 0.2, 0.2)下,随着耦合强度ρ2从0开始正向增大,系统一开始就进入混沌放电状态,直到ρ2=-0.7,期间存在周期窗口ρ2=0.1 6,ρ2=-0.51,随后通过反向倍周期分岔路径转为周期尖峰放电。李雅普诺夫指数谱表现的动力学状态分布与分岔图所展示的动力学基本一致。图10给出了不同突触耦合强度ρ2时,系统所产生的不同动力学现象,包括混沌、瞬态混沌、准周期以及周期行为。 图9 关于忆阻突触耦合强度ρ2动力学状态分布 从人工智能应用的角度来看,神经网络模型的电路实现具有重要的现实意义和必要性。通常,非线性动力学系统可以通过采用基本模拟电子电路实现。本节利用模拟运算放大器、模拟乘法器、电阻、电容对提出的局部有源忆阻突触耦合HR神经元网络进行电路设计与实现。基于图3的忆阻器电路和耦合HR神经元网络(9),局部有源忆阻突触耦合HR神经元网络电路如图11所示。其中,系统状态变量x1, y1, x2, y2, z通过5个电容积分器的输出电压表示。基于基尔霍夫电路定律,系统电路的等效电路方程为 图10 不同忆阻突触耦合强度ρ2所对应的多种动力学行为 图11 局部有源忆阻突触耦合HR神经元网络电路 假设C=10 nF, 根据系统参数与电路元件,部分电路元件阻抗值为:R=1 0 k Ω, R1=R6=R=10 kΩ, R2= R7=Rg/b=3.33 kΩ, R3= R8=Rg2/a =10 kΩ, R4= R9=Rg/c=2 kΩ, R5=R10=10 kΩ,RL1= Rg2/ρ1,RL2= Rg2/ρ2。为了验证数值仿真,在PSIM电路仿真软件中创建图12所示电路。仿真过程中,5个电容初始电压设置为(0.2V, 0.2V, 0.2V, 0.2V, 0.2V)。当I1=-0.05 mA,I2=0.25 mA, Ic=0.1 mA, ρ2=0.1, 相应的阻抗RL2= 100 kΩ, 调节不同的RL1,可以得到多种放电模式,如图13所示。当ρ1=-0.4,相应的阻抗RL1=25 kΩ,调节不同的RL2,可以得到不同的动力学行为,如图14所示。显然,在图13与图14的电路仿真结果很好地验证了图8与图10的数值仿真结果。 图12 忆阻耦合神经元网络PSIM仿真电路 图13 局部有源忆阻突触耦合HR神经元网络电路仿真结果 图14 局部有源忆阻突触耦合HR神经元网络电路仿真结果 本文设计了一种简单的局部有源忆阻器模型。通过理论分析、数值模拟以及电路实现,证明了该忆阻器的紧磁滞回线特征和局部有源属性。此外,利用该局部有源忆阻模型模拟生物突触特点,构建了一种局部有源忆阻突触耦合HR神经元网络。研究结果表明,该忆阻神经网络在不同的突触耦合强度下能表现出多种放电模式和混沌动力学行为,具有丰富的动力学特性。最后,通过采用模拟电子元件实现局部有源忆阻耦合HR神经元网络电路,并在PSIM电路仿真软件中得到新系统的多种放电行为和不同吸引子,从而证实了系统的有效性。
2.4 电路模型




3 局部有源忆阻突触耦合HR神经网络
3.1 模型建立



3.2 突触耦合强度相关动力学



4 电路设计与PSIM仿真验证


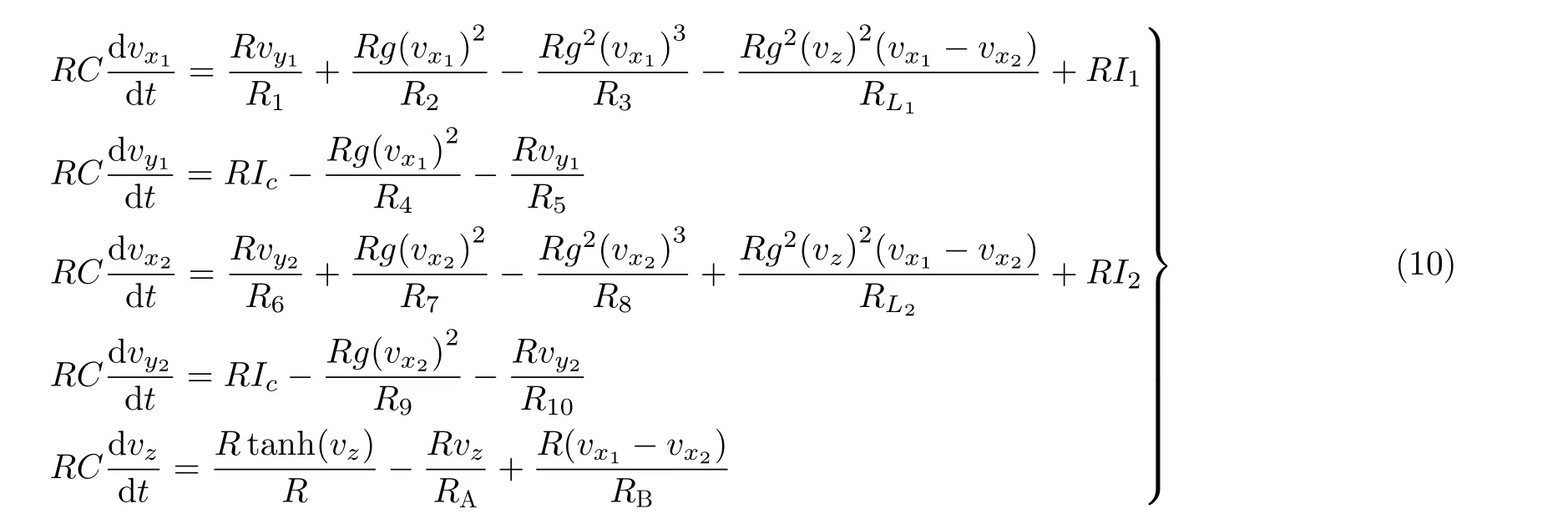



5 结束语
