基于模糊控制的永磁同步电机控制系统研究

姬浩然

（常州大学 微电子与控制工程学院，江苏 常州 213164）

伴随着绿色出行、低碳环保理念的推广，电动车在人们日常出行中逐渐占据主导地位。永磁同步电机（PMSM）具有简单的结构、较小的体积和较小的损耗，与传统直流电机相比，其依靠电力电子变换的器取代换向器和电刷，不会存在换向火花和机械磨损问题，因此被广泛应用于电动车上。永磁同步电机在多种工况下运行时，一方面电机的本体参数会有不同程度的变化，另一方面电机的负载也可能实时发生变化，从而使系统转动惯量发生改变，这些变化的参数都会影响系统的控制效果，削弱永磁同步电机的实际控制性能。因此如何实时对控制系统的PID 参数进行调整、实现系统最优控制成为了永磁同步电机控制的研究热点之一。

本文首先建立了永磁同步电机的数学模型，在此基础上进行了永磁同步电机模糊PID 设计，实时优化PI 参数，实现PI 参数的在线自整定，具有较好的实用意义和参考价值。

1 永磁同步电机的数学模型

永磁同步电机的结构由定子和转子两部分组成。定子结构与三相交流异步电机基本一致，转子部分由转子铁芯和永磁体组成。依靠电力电子变换器实现直流到交流的变换，取代了传统的电刷和换向器所组成的机械式换流器，从而避免了火花和机械磨损的出现。因此，永磁同步电机具有噪音小、使用寿命长的特点。

图1 中AX、BY、CZ 为在空间中对称分布的永磁同步电机定子三相绕组。以定子绕组中三相绕组的轴线作为参考坐标系的轴，可以建立一个三相静止坐标系，即ABC 三相静止坐标系。将永磁体的磁轴线N 极定为d 轴，垂直N 极定为q 轴，则可以得到一个固定在转子上的坐标系并将其命名为dq 轴坐标系。

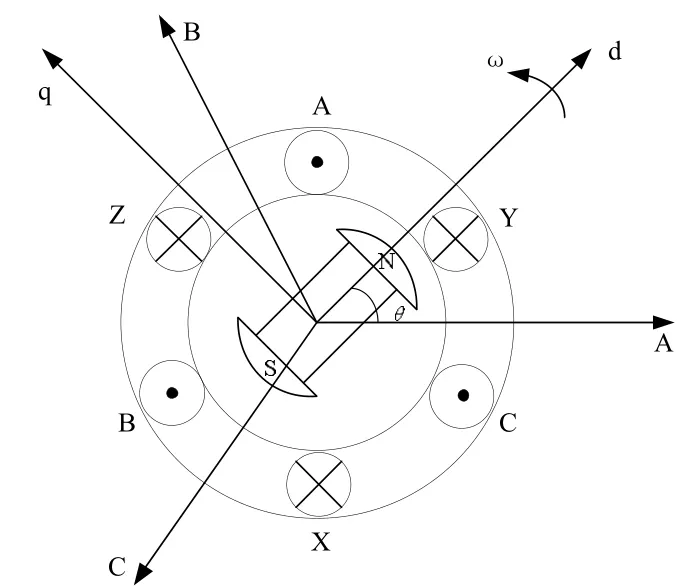
图1 永磁同步电机的绕组结构

磁链方程

式（1）中，Ψd、Ψq、Ψf别为 d 轴、q 轴、永磁体磁链；Ld、Lq分别为 d 轴电感和 q 轴电感；id、iq分别为 d 轴 q 轴电流。

电压方程

式（2）中，Ψd、Ψq为别为 d 轴、q 轴磁链，ud、uq为 d 轴和q 电压分量；R1为永磁同步电机定子相电阻，ω 为永磁同步电机角速度，p 为微分算子。

由公式（1）和（2）可以看出，永磁同步电机是一个多变量、强耦合的非线性系统，对其进行控制时需要对这些变量进行综合考虑。

2 模糊PI 控制设计

模糊控制和PI 控制相结合的算法结构框图如图2所示。其主要由模糊控制器和PI 控制器两部分组成，系统的误差e 和误差变化率ec为模糊控制器的输入，△Kp和△Ki为模糊控制器的输出，该输出作为PI 控制器的输入对Kp、Ki进行修正，实现PI 参数的实时整定。

图2 模糊PI 控制器原理框图

则PI 控制器的参数：

式（3）中，Kp和 Ki为修正后的 PI 参数，Kp0、Ki0为 PI 控制器根据电机静止状态时的参数所整定初始参数，△Kp、△Ki为模糊控制根据电机运行参数实时修正的PI参数变化量。

本文将模糊PI 控制用在永磁同步电机双闭环控制系统中速度环中。

根据模糊控制器的基本理论知识，结合永磁同步电机实际运行的工况按如下步骤设计模糊控制器：

第一步：确定输入输出变量的论域和模糊合集。

根据永磁同步电机速度环实际需要，将模糊控制器的控制结构设计成二输入二输出模式，控制结构的输入量为速度误差E 和速度误差变化率EC 输出量为速度环比例积分控制器参数整定量△Kp和△Ki。

模糊控制器输入输出变量的模糊合集的子集个数控制性能越好精度也就越高，但子集个数增加会占用更多的系统资源，增加实现的难度。在本文中，根据永磁同步电机实际控制精度要求，结合模糊集的结构，选择负大（NB）、负中（NM）、负小（NS）、零（ZO）、正小（PS）、正中（PM）、正大（PB）共七个级别作为本文所需的模糊集。

定义速度误差E、速度误差变化率EC 的模糊集合：

{NB、NM、NS、ZO、PS、PM、PB}

定义输出量△Kp和△Ki的模糊结合：

{NB、NM、NS、ZO、PS、PM、PB}

模糊控制器的粗糙程度由论域数值决定，过大的论域起不到调节效果，过小的论域会使调节速度变得缓慢。因此，本文将专家经验法和实验试凑法相结合，并根据永磁同步电机的结构特点选择模糊输入输出变量的论域，使模糊控制器输入变量的调节范围在+10和-10 之间，输出变量的调节范围在+1 到-1 之间。

定义速度误差E 和速度误差变化率EC 论域：

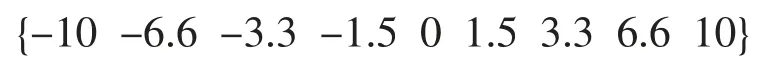
定义输出量△Kp和△Ki的论域：

第二步：清晰量模糊化及确定隶属度函数。

模糊控制器输入为清晰量，先进行模糊化，将模糊变化量控制在输入论域范围内，量化因子根据公式（4）确定：

式中，K1为速度误差E 的量化因子，K2为速度误差变化率EC 的量化因子；aE为速度误差E 的论域范围，aEC为速度误差变化率EC 的论域范围；NE为速度误差E的模糊集合的个数，NEC为速度误差变化率EC 的模糊集合的个数。

根据永磁同步电机速度控制特点，本文取K1=0.01，K2=0.0001 作为量化因子。

本文选择了三角隶属度函数作为速度环模糊控制器的隶属度函数，如图3 所示，其中图3（a）为速度误差E 和速度误差变化率EC 的隶属度函数，图3（b）为△Kp和 △Ki隶属度函数。

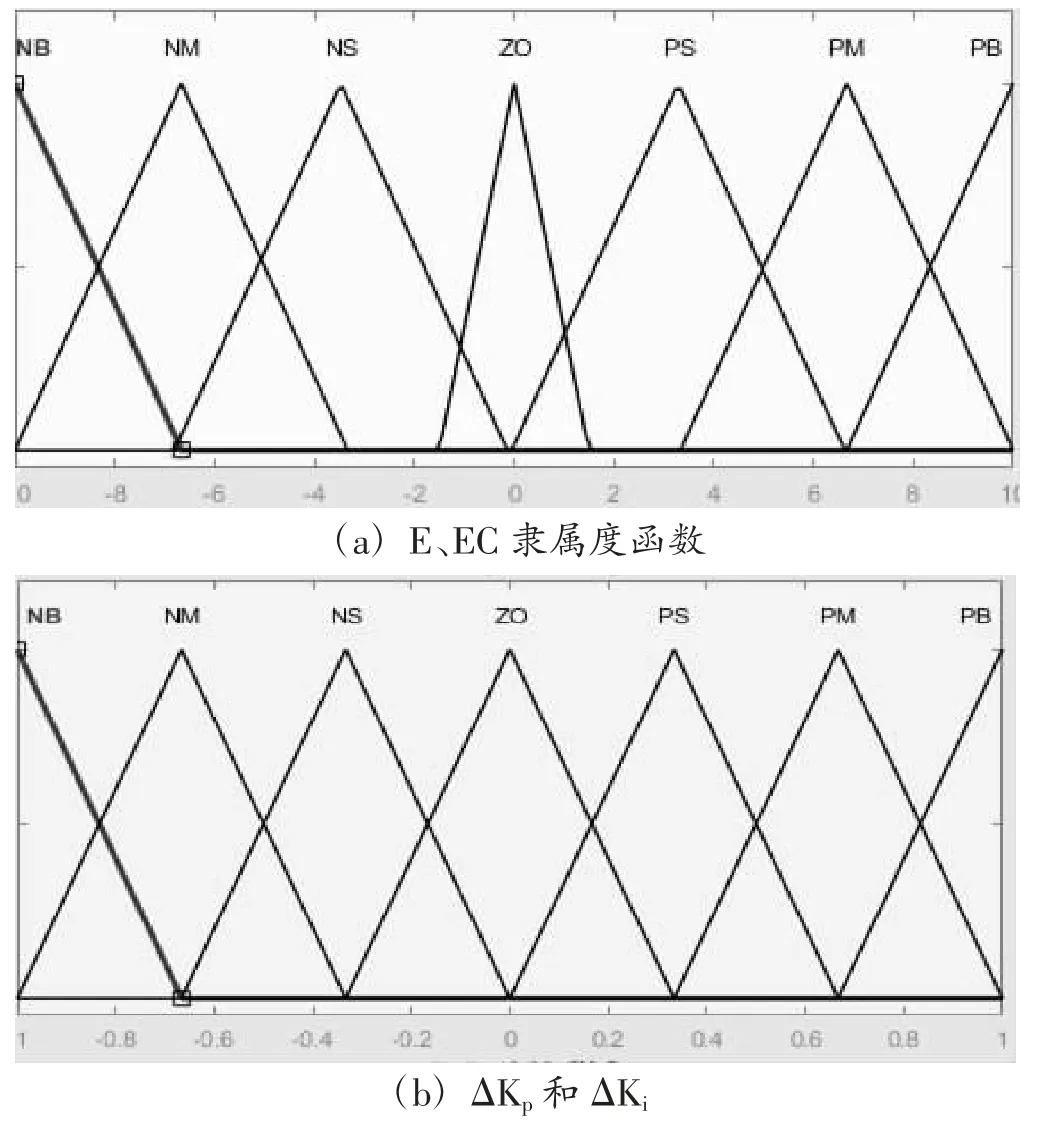
图3 隶属度函数

第三步：模糊规则。

根据PI 参数的整定要求，结合永磁同步电机控制特点，得到△Kp和△Ki的模糊控制规则，见表1、表2。

表1 △Kp 的模糊控制规则表

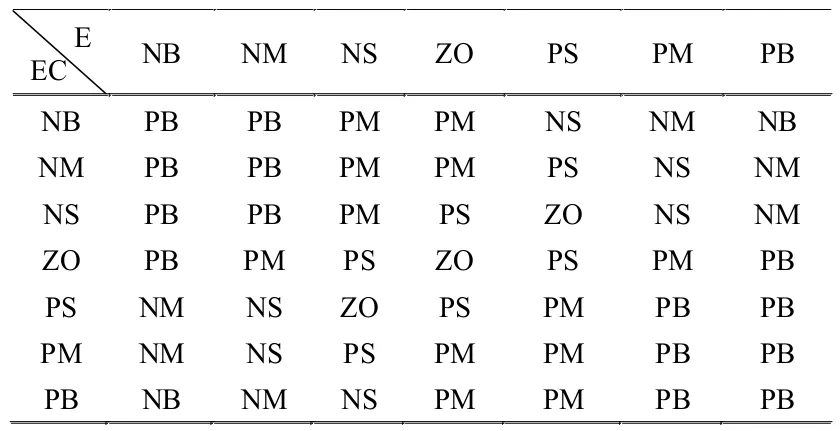
表2 △Ki 的模糊控制规则表

第四步：去模糊化。

模糊推理运算得到的结果为模糊输出量，该结果需要进行解模糊运算，本文中采用重心法进行解模糊，求解后得到变量μ。

式中，μ 为输出量清晰量，μi为各组元素的权重。

3 PMSM 系统控制器仿真与分析

在Matlab 中选择额定功率为3kW 的凸极永磁同步电机，电机的额定转速为1200rpm，定子电阻为0.958Ω，直流母线电压Udc为311V。具体电机参数如表3 所示。

表3 仿真电机参数

在Simulink 中建立的仿真模型如图4 所示，给定速度1000rad/s，与速度反馈信号经过比较器运算得到速度误差E、速度误差变化率EC，经过速度环的模糊控制处理后，作为q 轴电流环的给定，d 轴电流给定为0。

图4 基于模糊PI 控制的PMSM 仿真模型

模糊PI 控制器的SimuLink 模型如图5 所示，设量化因子Ke=0.01，Kec=0.0001，比例因子分别为Lp=7，Li=3.5，图 6 为 △Kp和 △Ki生成的三维模糊规则图。

图5 模糊PI 控制器的SimuLink 模型

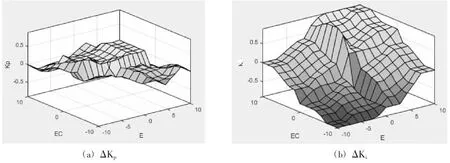
图6 三维模糊规则图

为了验证模糊PI 控制器的性能，在负载突变情况下，对控制系统的控制效果进行了仿真。

由图7 和图8 可知空载启动时，基于传统PI 控制的电机的转矩在0.002s 上升至限幅值，电机转速在0.03s 达到给定值1000rpm，进入稳定状态，而在模糊PI 控制中，转矩在0.002s 上升至限幅值，电机速度在0.019s 达到给定值1000rpm，进入稳定状态后电磁转矩迅速降低，直至转矩等于摩擦转矩0.84N·m。在0.1s负载转矩从0 阶跃到12N·m，电机电磁转矩迅速上升，然后快速稳定在12.84N·m，电机转速略微下降后迅速恢复至给定值。突加负载后，系统能够快速反应，输出转矩快速跟随负载转矩，转速能够迅速跟随。使得系统恢复稳定状态。

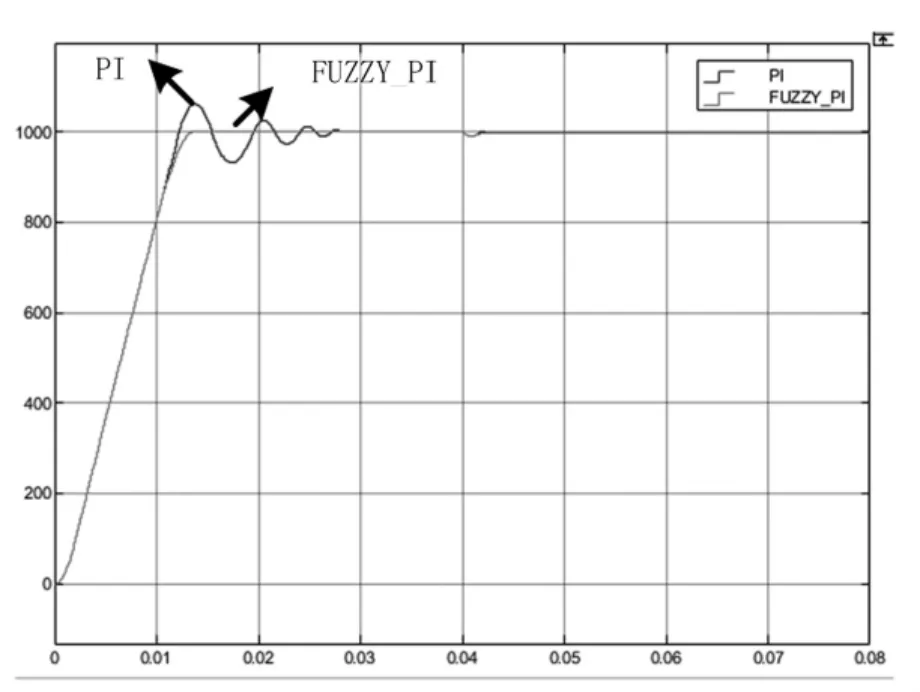
图7 电机突加负载速度响应对比

图8 突加负载转矩对比图

4 结论

本文根据永磁同步电机运行时参数容易变化的特点，将模糊控制应用于控制系统当中，设计了基于模糊的PI 控制器用于速度环的控制，实时调整速度环的比例、积分的增益。在Matlab 中建立了基于模糊PI 控制的永磁同步电机控制系统模型，在负载变化的情况下对模型进行了仿真，仿真结果表明模糊PI 控制器与传统的PI 控制器相比能有效提高速度环相应速度。