基于人工神经网络的亚格子应力建模1)
2021-12-02肖左利
吴 磊 * 肖左利 *,
* (北京大学工学院力学与工程科学系,北京 100871)
† (湍流与复杂系统国家重点实验室,北京 100871)
引言
大涡模拟(large-eddy simulation,LES)是湍流研究中一种重要的数值模拟方法[1].与直接数值模拟(direct numerical simulation,DNS) 和雷诺平均(Reynolds-averaged Navier-Stokes,RANS)方法相比,大涡模拟可以在分辨率相对较低的网格上对大尺度湍流运动进行模拟,能够在较低的计算成本下解析部分湍流结构.近年来在航空航天、多相流动、湍流燃烧与传热等众多工程领域得到广泛应用[2].
在大涡模拟方法中,通过滤波技术可将湍流脉动分解为可解尺度与亚格子尺度(subgrid-scale,SGS)流场.在不可压缩流动中,亚格子尺度流动对可解尺度流动的影响由亚格子应力张量表达[3-5].如何使用可解尺度流场信息表示亚格子应力张量成为大涡模拟方法的关键科学问题之一.传统亚格子模型在湍流理论和假设的基础上,利用可解尺度流场显式表达亚格子应力,主要包括Smagorinsky 模型[6]、动力Smagorinsky 模型[7-9]、相似模型[10-12]、梯度模型[11-13]、混合模型[10-11,14]、优化模型[15-17]、变分多尺度方法[18]、一方程模型[19]和二阶矩模型[20]等.这些模型虽然已经应用于各种流动的仿真计算,但仍有诸多缺点等待解决.例如,Smagorinsky 模型耗散过大;相似模型提供了过多的反传(backscatter),不能充分耗散能量,因此常常伴随着计算发散或不准确现象;梯度模型在网格较密时较为准确,但该模型随着网格尺度的增大而变得不稳定.上述模型的动力及混合版本可以有效解决能量耗散问题,并在大多数情况下可以得到更准确的结果,但这些模型伴随着较高的计算成本,且普适性较差.因此,有必要发展新的亚格子模型.
传统亚格子模型的构建多基于湍流物理和假设,目前基本陷入瓶颈期[21].然而,计算机性能和实验测试手段的发展使得研究者积累了大量高精度、高分辨率的计算和实验数据.如何利用这些数据建立更高精度的亚格子模型,成为当前的研究热点之一.随着人工智能时代的到来,神经网络等机器学习方法已广泛应用于图像识别[22]、自动驾驶[23]和生物信息学预测[24]等领域,并在湍流建模[25-27]、流动控制[28]和气动优化[29]等流体力学领域取得了一定成果[30-31].有鉴于此,本文利用人工神经网络(artificial neural networks,ANN)开展亚格子应力的建模研究.
目前有关机器学习的大涡模拟模型研究,主要集中于均匀各向同性湍流及槽道流.在二维衰减的各向同性湍流中,Maulik 等[32-33]等使用全连接神经网络(fully connected neural network,FCNN)模型预测反卷积的涡量和流函数[32]及亚格子应力[33],结果表明FCNN 模型在湍动能谱方面较Smagorinsky 模型等传统LES 模型有着更高的预测精度.对于不可压缩的三维各向同性湍流,Vollant 等[34]同样利用FCNN 建立滤波后的应变率张量和亚格子标量通量的散度之间的关系,预测结果接近于滤波后的DNS 数据(fDNS).Zhou 等[35]考虑了变滤波尺度的模型构建问题,他们所建立的模型能够预测不同滤波尺度下的亚格子应力.Xie 等[36]使用空间人工神经网络(spatial artificial neural network,SANN)建立了亚格子应力的预测模型,模型在先、后验中均有较好表现.Yuan 等[37]基于反卷积人工神经网络(deconvolutional artificial neural network,DANN) 对亚格子应力进行建模,后验结果表明DANN 能够给出更为准确的速度统计量及流动结构.Wang 等[38]分别使用随机森林和ANN 方法建立了滤波速度及其一阶、二阶偏导数与亚格子应力的映射关系,后验结果优于动力Smagorinsky 模型.在可压缩三维均匀各向同性湍流中,Xie 等[39-41]等利用 FCNN 对亚格子力和亚格子热通量的散度[39],混合模型的系数[40]和亚格子应力及亚格子热通量[41]开展预测研究,结果表明基于FCNN 的LES 模型能够得到比动力Smagorinsky 模型及动力混合模型更高精度的能谱和速度结构函数.针对槽道流的大涡模拟,Sarghini 等[42]使用FCNN 预测尺度相似和Smagorinsky 混合模型中Smagorinsky 项的系数,以保证大涡模拟计算的准确性和计算效率.值得注意的是,Sarghini 等[42]的工作是基于大涡模拟计算数据而非fDNS 数据.Gamahara 和Hattori[43]首次将ANN用于槽道流亚格子应力的模化,他们考虑了组不同的输入,其中是滤波速度的旋转张量.他们的研究结果表明使用作为输入时,ANN 亚格子应力模型与fDNS 的相关系数最高,甚至高于梯度(非线性)模型.然而在后验中并没有得到优于Smagorinsky 模型的结果,因此并没有解决传统亚格子模型中先、后验表现不一致[1]的现象.Park 和Choi[44]同样研究了FCNN 中不同输入对模型先、后验结果的影响,结果表明先验表现不佳的输入所构建的模型反而能够给出更为准确的后验结果.
根据亚格子应力的涡黏假设可知,亚格子应力除取决于可解尺度流场外,还依赖于滤波尺度.Zhou 等[35]在均匀各向同性湍流中考虑了含滤波尺度的亚格子应力模化问题,所建立的模型能够实现不同滤波尺度下亚格子应力的预测.然而,在槽道流中缺乏对变滤波尺度亚格子应力模型的系统研究.因此,本文使用ANN 方法,针对不可压缩槽道流中的亚格子应力开展建模工作,使得模型能够预测不同滤波尺度下的亚格子应力,并对该模型开展相应的后验研究.

图1 ANN 模型框架Fig.1 The framework of ANN model
1 数据驱动的亚格子应力建模框架
不可压缩流动的大涡模拟控制方程如下


2 数据准备
2.1 DNS 数据的准备与验证
模型训练与测试均需要槽道流的fDNS 数据,因此先要对槽道流开展DNS 计算.如图2 所示,x,y,z轴分别代表流向、法向与展向.流向与展向采用均匀网格并施加周期性边界条件,法向采用双曲正切函数生成的非均匀网格.本文使用了可压缩流动求解器,通过设置特征马赫数为0.2 来近似不可压缩流动.因此,在壁面处(y=±1)使用无滑移及等温边界条件.采用有限差分方法开展DNS 计算,对流项采用Steger-Warming 流通矢量分裂的7 阶迎风格式,黏性项采用8 阶中心差分格式离散.时间推进采用3 阶 Runge-Kutta 方法,其中时间步长由CFL 条件决定.为了使流动达到充分发展状态,流动由均匀的体积力驱动,其中体积力根据指定的质量流量而随时间变化.
图2 槽道流计算区域示意图Fig.2 Schematic for computational domain of turbulent channel flow
本文考察3 组不同的雷诺数.以入口平均速度(bulk velocity)Ub为特征速度的雷诺数Reb=Ubδ/γ分别为2800,5000 和7000,其中 δ 为半槽宽.对应以壁面摩擦速度uτ为特征速度的雷诺数Reτ=uτδ/γ 大致为180,300 和395,其中uτ=(τw/ρ)1/2,壁面切应力 τw=(ρν)∂u/∂y.表1 列出了DNS 的参数,其中Lx,Ly,Lz分别为3 个方向的计算域长度,Δx+与 Δz+为流向和展向使用黏性长度(viscous lengthscale)δν=ν/uτ无量纲化的均匀网格间距,分别表示法向使用 δν无量纲化的最小和最大网格间距,Nx,Ny,Nz为3 个方向的网格数.图3 为DNS结果,其中图3(a)为槽道流的平均速度剖面,图3(b)和图3(c)为槽道流雷诺应力剖面,与文献[45-46]的计算结果基本吻合.

表1 DNS 计算参数Table 1 Computational parameters of DNS
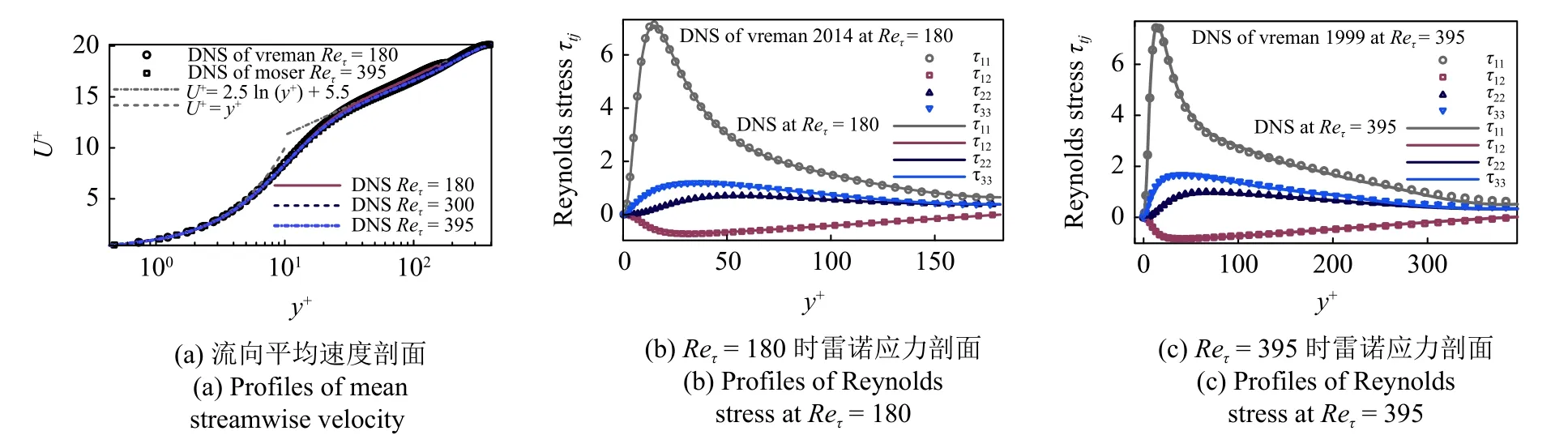
图3 DNS 计算结果Fig.3 DNS results
2.2 离散滤波方法
在DNS 完成后,需要对DNS 数据进行滤波操作以得到fDNS 流场信息.以一维滤波为例,在连续空间中对物理量的滤波由下式表达
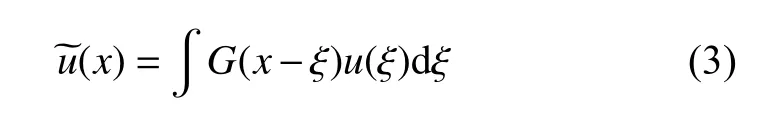
其中,G为滤波函数.式(3)并不适用于离散点的滤波,故有必要在离散空间发展相应的滤波表达式
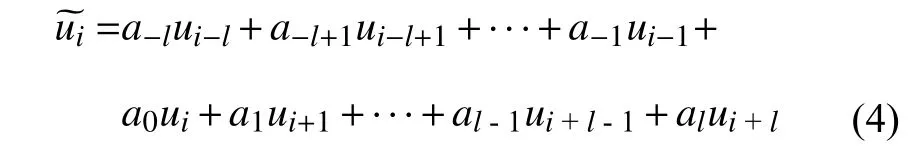
其中,l为离散滤波使用的基架点个数.Sagaut 和Grohens[47]利用泰勒展开式推导了不同滤波函数下滤波量的微分表达式,对盒式滤波器来说

3 人工神经网络
3.1 基本原理与输入输出变量的选择
本文使用前馈人工神经网络[48]建立可解尺度流场与亚格子应力的映射关系.图4 为网络结构示意图.
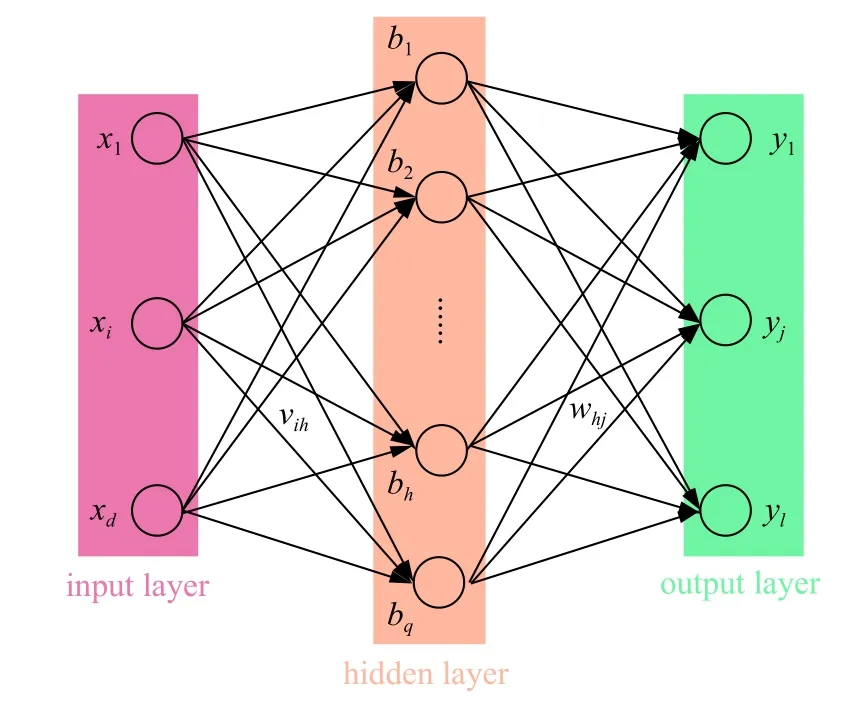
图4 前馈人工神经网络示意图Fig.4 Schematic of the feedforward ANN
假设将d个可解尺度流场变量作为输入量x=[x1,x2,···,xi,···,xd]T,由神经元模型可知,隐藏层第h个神经元接收到的输入为
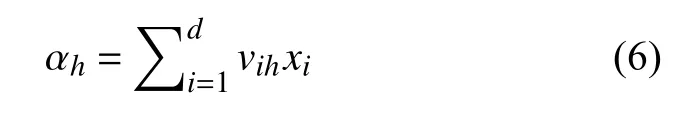
其中,vih为输入层第i个神经元与隐藏层第h个神经元之间的连接权重.输出层第j个神经元接收到的输入为

其中,wh j为隐藏层第h个神经元与输出层第j个神经元之间的连接权重.因此,神经网络输出层第j个神经元的输出值为

其中f为输出层的激活函数,θj为输出层第j个神经元的偏置.借助误差逆传播算法[49-50],不断调整网络权重与偏置,使得网络输出与DNS 亚格子应力最为接近.
除特别声明外,本文所采用的输入特征为x=[Δf∂ui/∂xj,Δ,y]T,其中i,j=1,2,3,并使用单层128 个神经元作为隐藏层.考虑到DNS 亚格子应力分量 τ13与 τ23接近于零,故本文仅针对亚格子应力分量 τ11,τ12,τ22及 τ33分别建立ANN 模型.
3.2 网络超参数的设定
为防止模型训练过程中出现过拟合,本文为损失函数添加惩罚项,具体表达式如下

其中第一项为预测值与真实值的均方根(RMS)误差,第二项为L2正则化项,n为样本数,Yi和Ti分别为第i个样本的真实值和预测值,w是模型的权重,λ为正则化系数.
本文采用ReLu 激活函数,表达式如下[51]

可以有效缓解梯度消失问题且计算效率高,近些年得到了广泛应用.
Adam 算法是目前深度学习领域内的流行算法,因此本文采用Adam 算法进行网络权重与偏置系数的调整.同时,Loshchilov 和Hutter[52]的研究表明Adam+学习率的动态衰减可以提高Adam 的算法性能.因此,本文在采用Adam 作为优化器算法的同时,还在训练过程中动态调整学习率.
4 模型的训练与先验测试
4.1 不同滤波尺度下的训练与先验测试
如前所述,对于3 个不同雷诺数的DNS 流场而言,均可得到在5 个滤波尺度下的fDNS 数据及对应的亚格子应力.为了考察滤波尺度的影响,首先对相同雷诺数下不同滤波尺度的数据开展训练,具体如表2 所示.
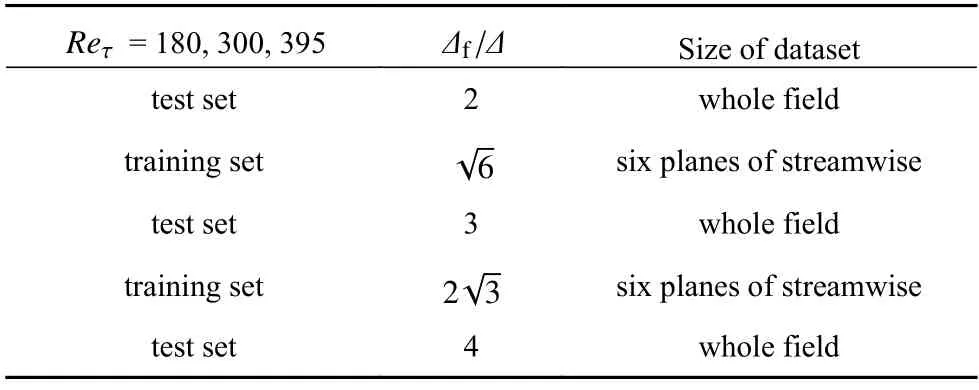
表2 相同雷诺数下不同滤波尺度ANN 模型训练及测试集Table 2 Training and test sets of ANN model at the same Reynolds number and different filter widths
本文模型训练在基于Tensorflow 和Theano 的开源深度学习库Keras 中展开.利用训练的ANN 模型可以预测得到测试集下的亚格子应力.下面从不同方面评估模型的预测结果.
4.1.1 亚格子应力
首先考察ANN 模型的建模项,亚格子应力.可绘制DNS 与ANN 的亚格子应力云图以直观比较二者的分布差异.为了对比分析,本文还计算了两个常用的LES 模型,即Smagorinsky 模型[6]与梯度模型[11,13]的亚格子应力.在Smgorinsky 模型中,亚格子应力由下式表达

以Reτ=180,Δf/Δ =4 的测试结果为例,给出了y=0.9 截面上对角线分量 τ11与非对角线分量 τ12的亚格子应力云图,如图5 所示.可以看出ANN 模型能够精确地预测出真实的亚格子应力分布,而梯度模型和Smagorinsky 模型与DNS 亚格子应力存在较大偏差.
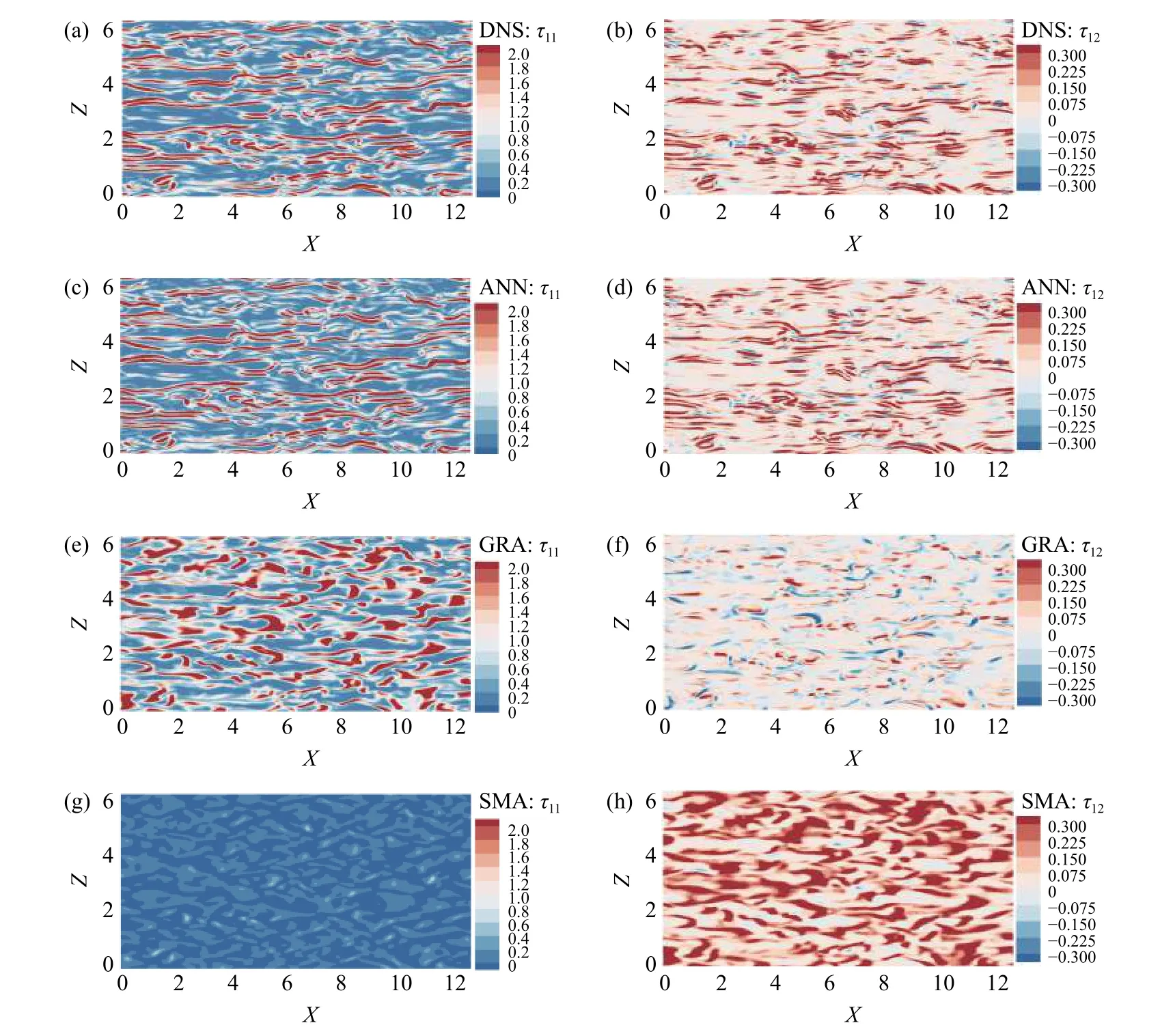
图5 R eτ =180,Δ f/Δ =4 时 y =0.9 截面上亚格子应力分量 τ 11 及 τ 12 的分布云图.(a,b) DNS;(c,d) ANN 模型;(e,f)梯度模型;(g,h) Smagorinsky 模型Fig.5 Contours of the SGS stress components τ 11 and τ 12 at R eτ =180,Δ f/Δ =4 and y =0.9.(a,b) DNS;(c,d) ANN model;(e,f) gradient model;(g,h) Smagorinsky model
在槽道流中,常常对物理量 φ 进行流向和展向平均并研究其随法向的变化规律,计算方法如下

以Reτ=180 ,Δf/Δ=2 时的测试结果为例,绘制DNS 与ANN 模型的亚格子应力在xz平面内的平均值及其脉动的均方根剖面,如图6 所示.从图6 中可以看出,ANN 模型的亚格子应力与DNS 高度吻合.因此,尽管ANN 模型并未在 Δf/Δ=2 滤波尺度下训练,且该滤波尺度在训练集所涵盖的滤波尺度之外,但是ANN 模型依然能够给出正确的亚格子应力均值及均方根值.
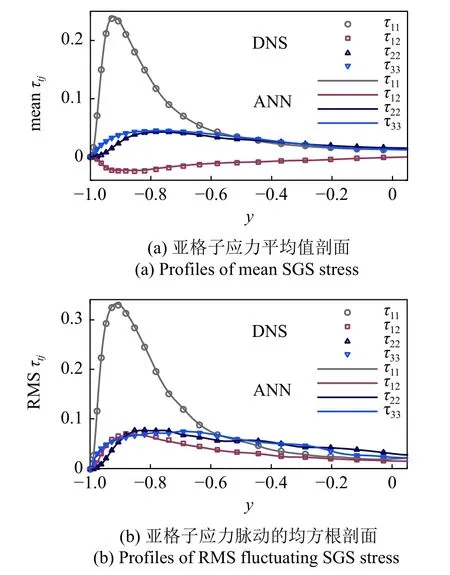
图6 R eτ =180,Δ f/Δ =2 时DNS 与ANN 模型的亚格子应力平均值及其脉动的均方根剖面Fig.6 Profiles of mean SGS stress and RMS fluctuating SGS stress obtained from DNS and ANN model at R eτ =180,Δ f/Δ =2
相关系数是LES 亚格子模型先验测试的一个重要衡量指标,在槽道流中,相关系数定义如下


图7 R eτ =180,Δ f/Δ =3 时各模型与DNS 亚格子应力的相关系数剖面(横坐标: y)Fig.7 Profiles of correlation coefficient between modeled SGS stress and DNS data at R eτ =180,Δ f/Δ =3 (x-coordinate: y)

图8 R eτ =180,Δ f/Δ =3 时各模型与DNS 亚格子应力的相关系数随 y+ 的变化剖面(横坐标:y+)Fig.8 Profiles of correlation coefficient between modeled SGS stress and DNS data at R eτ =180,Δ f/Δ =3 (x-coordinate: y+)
通过相关系数剖面可进一步计算空间平均的相关系数
以此计算了3 个雷诺数下共9 个测试算例的空间平均相关系数,结果如表3 和图9 所示.可以看出,对3 个雷诺数的所有测试算例来说,ANN 模型与DNS 的相关系数都几乎接近于1,而梯度模型和Smagorinsky 模型与DNS 的相关系数大致在0.65和0.25 左右.这再次证明ANN 模型能够成功地利用可解速度场模化出较为真实的亚格子应力,并且在滤波尺度上有着很好的泛化性能,解决了Gamahara 和Hattori[43]遇到的模型无法推广至其他滤波尺度的问题.此外,随着滤波尺度的增大,梯度模型及Smagorsisky 模型的相关系数都有一定程度的下降,这与Zhou 等[35]在均匀各向同性湍流中观察到的现象类似,而ANN 模型的下降程度并不明显.

表3 亚格子应力空间平均相关系数Table 3 The spatial averaged correlation coefficient of SGS stress
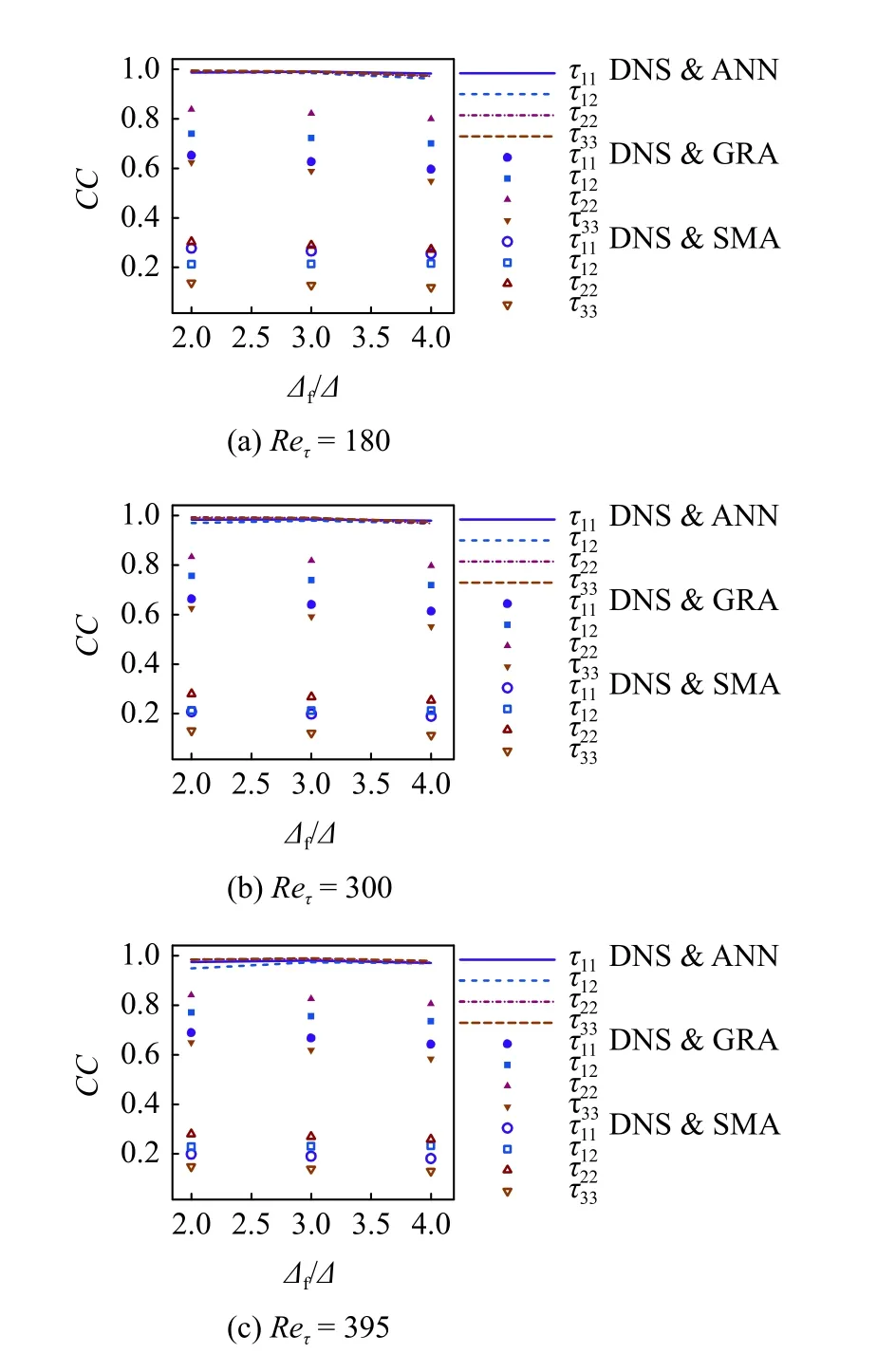
图9 亚格子应力空间平均相关系数Fig.9 Spatially-averaged correlation coefficients between the modeled and DNS SGS stresses
以上是关于ANN 的建模项,即亚格子应力与真实应力的相关性评估.在槽道流中,还存在一些对LES 具有重要影响的物理量[53-55],下面对ANN 模型在相关方面的预测能力进行分析讨论.
4.1.2 其他亚格子物理量
可解速度场湍动能Ef的输运方程如下[1]
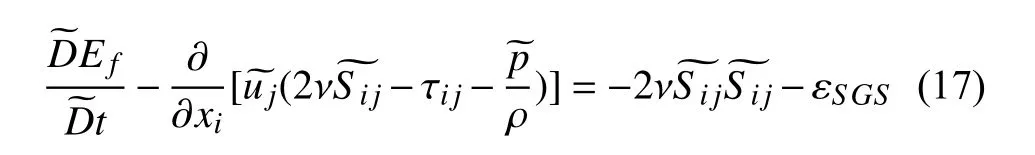

图10 R eτ =300 时3 个测试算例的平均亚格子耗散剖面Fig.10 Profiles of mean SGS dissipation for the three test cases at R eτ =300
平均来讲,能量由可解尺度向亚格子尺度传递.然而在壁湍流尤其是其缓冲层中,能量由亚格子尺度向可解尺度传递,该现象称作亚格子能流反传(SGS backscatter).湍流理论表明,在壁湍流中,亚格子反传与上抛(ejections)和下扫(sweeps)现象密切相关[57-58].传统的LES 涡黏模式并不能够捕捉壁湍流中的反传[57],因此ANN 模型是否能够精确预测亚格子反传值得关注.当存在亚格子反传时,亚格子耗散 εSGS<0,因此可用εSGS-back=(εSGS-|εSGS|)/2 来表示亚格子反传.图11 为Reτ=300 时3 个测试算例的平均亚格子反传.可以看出ANN 模型能够准确给出真实的亚格子反传,梯度模型虽能够给出反传随着壁面坐标y+的变化趋势,但极大地高估了亚格子反传的峰值,且出现峰值的位置也存在较大偏差,这与Balarac 等[59]的结论基本一致.较大的反传容易导致LES 计算的不稳定,本文结果再次印证了梯度模型容易导致计算不稳定的观点[60].
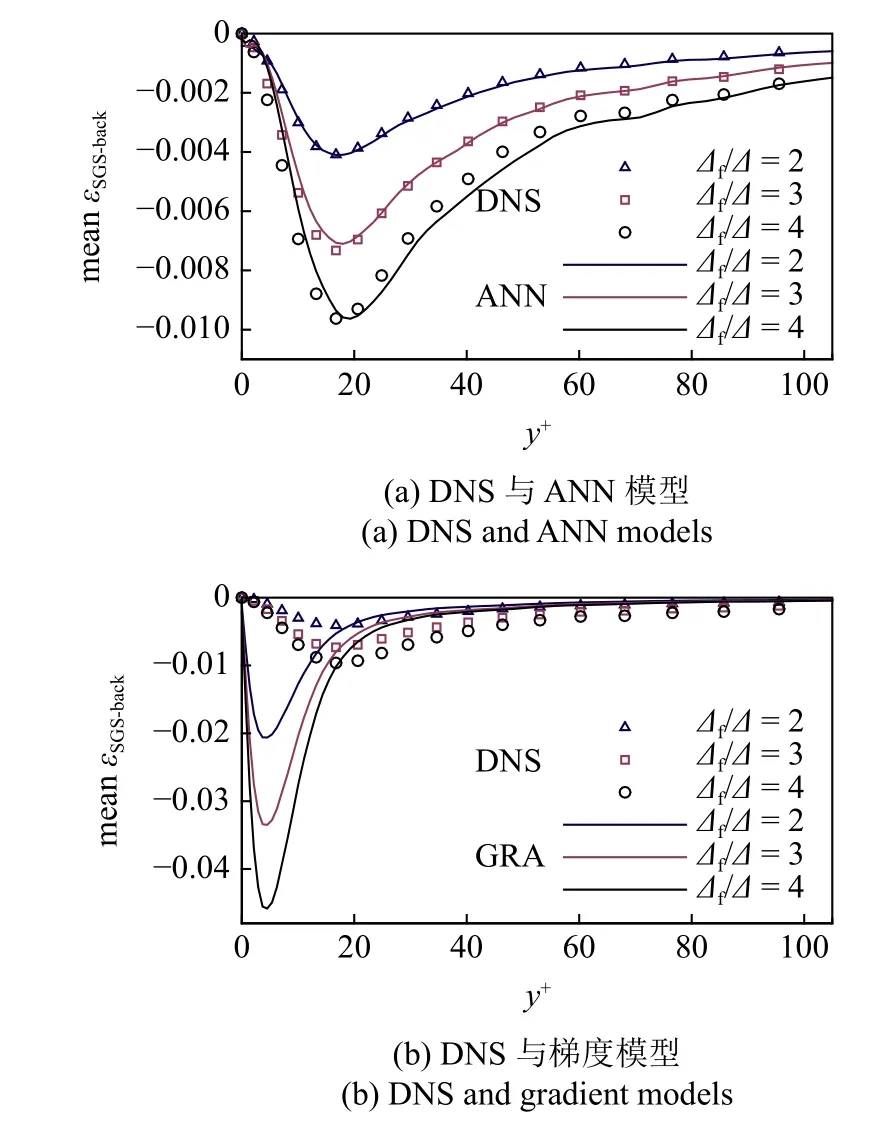
图11 R eτ =300 下3 个测试算例的平均亚格子反传剖面Fig.11 Profiles of mean SGS backscatter for the three test cases at R eτ =300
由式(2)可知,亚格子应力实际上以散度形式∂τi j/∂xj出现在动量方程中,称为亚格子力(SGS force).现考察模型对亚格子力的预测能力.以流向动量方程的亚格子力 ∂ τ1j/∂xj为例,图12 为Reτ=300 时3 个测试算例的平均亚格子力.可以看到,尽管ANN 模型在峰值处略微低估了亚格子力,但仍然能够很好地预测出亚格子力随壁面坐标y+的变化趋势,相比于梯度模型有了极大提高.
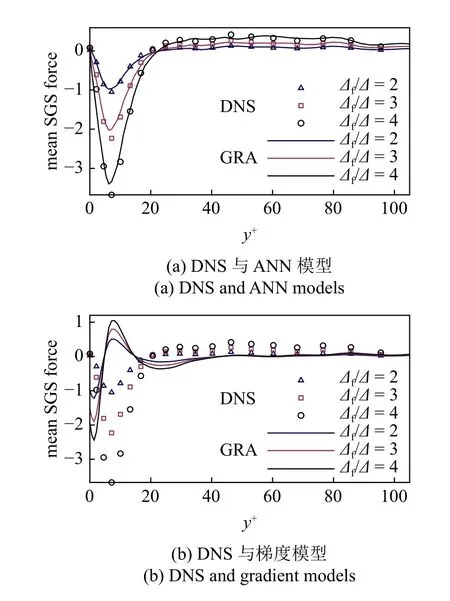
图12 R eτ =300 下3 个测试算例的平均亚格子力 ∂ τ1j/∂xj 剖面Fig.12 Profiles of mean SGS force ∂ τ1j/∂xj for three test cases at R eτ =300
Völker 等[61]指出,亚格子输运对于开展精确的LES 具有重要影响.图13 为Reτ=300 时3 个测试算例的平均亚格子输运.从中可以看出ANN 模型的计算结果与DNS 高度吻合.
此外,计算了3 个雷诺数下共9 个测试算例的



图15 DNS 与ANN 模型的亚格子应力平均值剖面Fig.15 Profiles of mean SGS stress obtained from DNS and ANN model

表5 亚格子应力空间平均相关系数Table 5 Spatially-averaged correlation coefficient of SGS stress
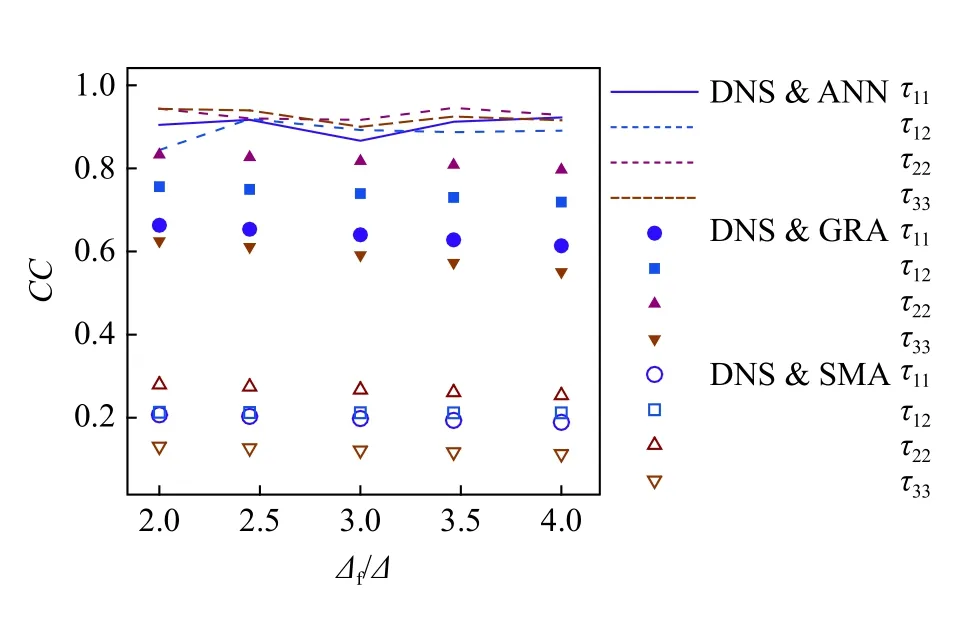
图16 亚格子应力空间平均相关系数Fig.16 Spatially-averaged correlation coefficient of SGS stress
5 不同滤波尺度下的后验测试
4.1 节对2~4 倍DNS 网格尺度 Δ 下的fDNS数据进行了ANN 模型的先验测试.本节基于该模型,在3 个雷诺数下分别开展ANN 模型的LES 后验计算.本文LES 计算为隐式滤波,故LES 计算的网格尺度分别为DNS 网格尺度 Δ 的2~4 倍.控制方程为式(1)和式(2),其中方程(2)中 τij由ANN 模型在计算过程中实时给出.根据对比分析需要,本文在相应网格尺度下同时利用带壁面衰减函数[62]的Smagorinsky 模型[6]、梯度模型[11,13]及ILES 方法[63-64]开展了数值模拟,数值方法与2.1 节中提到的DNS计算保持一致.计算过程中槽道的质量流量保持不变,因此摩擦雷诺数Reτ取决于亚格子模型.表6 列出了各个算例在计算稳定后的Reτ值.图17 为相应的相对误差,误差计算公式如下
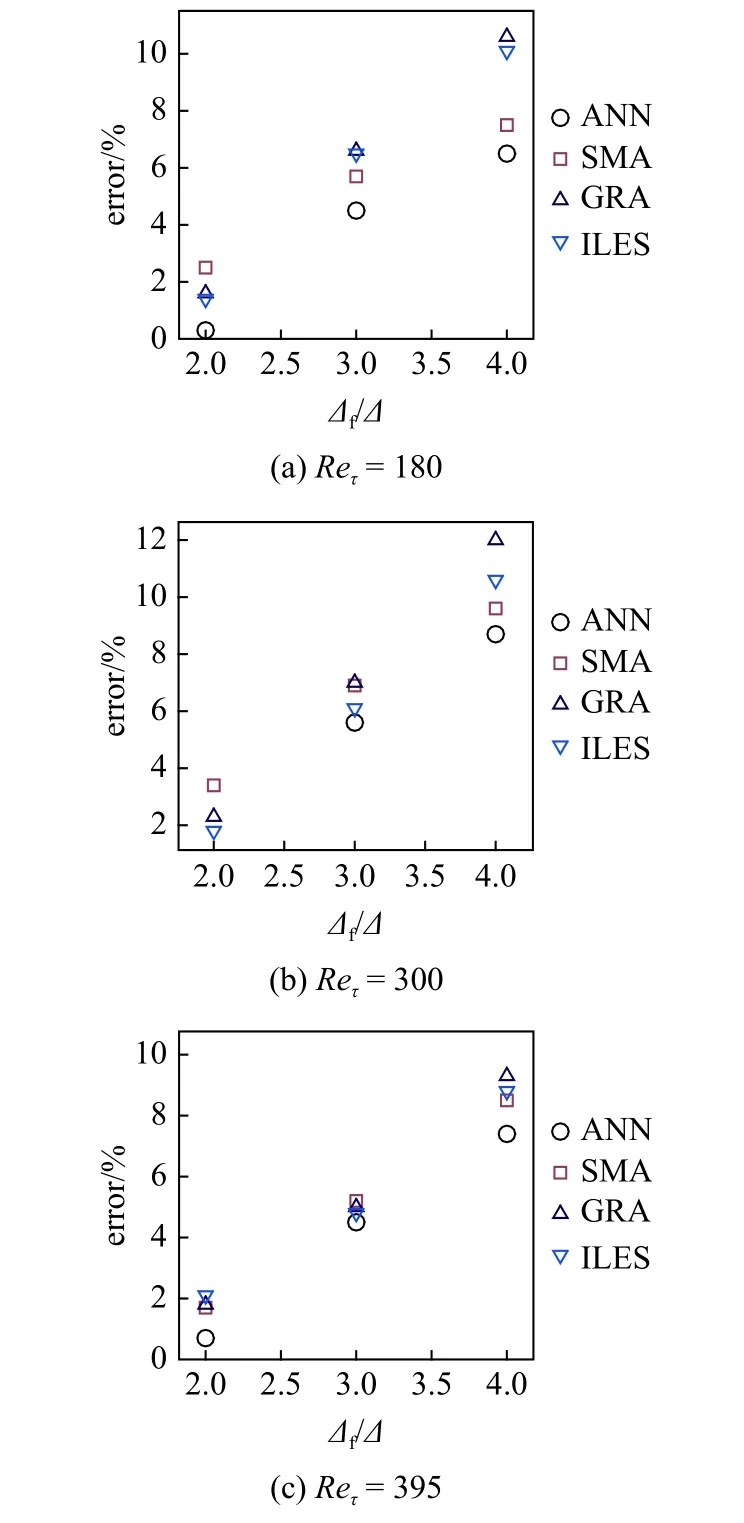
图17 各个后验算例计算稳定后 R eτ 值的相对误差率Fig.17 The relative errors of R eτ for a posteriori test cases at statistically steady state

表6 各个后验算例计算稳定后的 R eτ 值Table 6 Values of R eτ for a posteriori test cases at statistically steady state
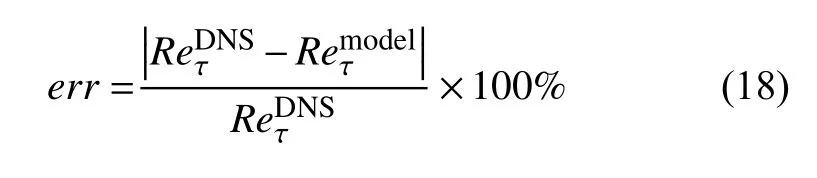
以Reτ=180 为例,绘制不同模型在3 套网格下的流向平均速度剖面,如图18 所示.可以看出,相比于Smagorinsky 模型、梯度模型及ILES 模型,基于ANN 模型得到的流向平均速度剖面更接近于DNS结果.观察梯度模型及Smagorinsky 模型的先、后验结果可以发现,尽管梯度模型在先验相关系数上优于Smagorinsky 模型,但后验表现并不如Smagorinsky 模型.也就是说,传统LES 模型中存在着先后验不一致的现象:亚格子应力先验的高相关性并不意味着亚格子模型后验计算的成功[1,44,65].对比ANN模型的先、后验结果发现,尽管随着LES 网格尺度的增大,ANN 模型与传统LES 模型一样均出现一定程度的精度下降,但ANN 模型有效解决了先后验不一致的现象,不仅给出了明显优于传统LES 模型的先验结果,在后验计算上也有一定提升.
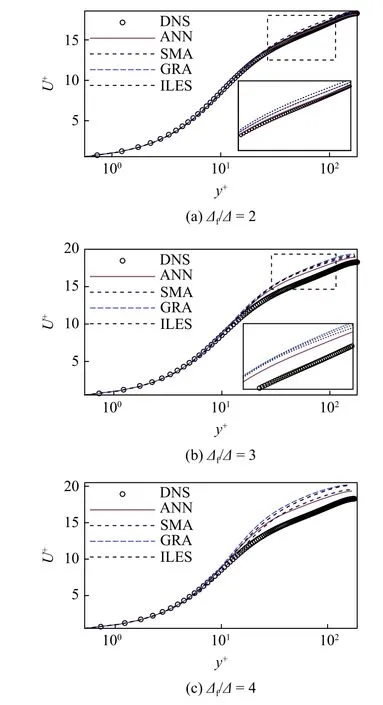
图18 不同模型在3 个网格尺度下的流向平均速度剖面Fig.18 Profiles of mean streamwise velocity obtained using different models at three grid scales
为了进一步检验ANN 模型在预测脉动速度方面的能力,计算了3 组网格尺度下各个脉动速度分量的均方根值在垂直壁面方向的分布,并与其他模型(包括Smagorinsky 模型、梯度模型及ILES 方法)的计算结果以及滤波后的DNS (fDNS)结果进行了比较.各种方法获得脉动速度均方根剖面如图19所示.观察各个模型在不同网格尺度下对3 个脉动速度分量预测上的表现可以发现,虽然ANN 模型的性能整体上相对其他3 个模型有所提升,但是在某些法向位置的表现不如其他LES 模型.特别地,随着网格尺度的增大,本文的ANN 模型所预测结果与fDNS 结果的偏差会逐渐增大.这与现有参数化模型的后验表现一致[66].引起此类现象的原因之一可能是平行于壁面方向与垂直壁面方向的网格长宽比过大[67].因此,ANN 模型在后验,尤其是在预测速度高阶量等方面的表现仍然值得进一步研究.

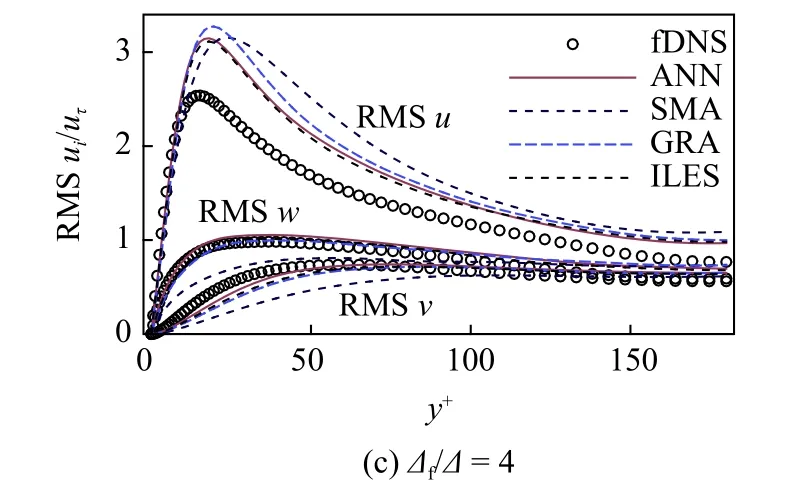
图19 不同模型在3 个网格尺度下脉动速度均方根剖面Fig.19 Profiles of RMS fluctuating velocity obtained using different models at three grid scales
6 结论
本文使用人工神经网络方法,考虑滤波尺度及雷诺数影响,对槽道湍流大涡模拟的亚格子应力模型开展研究,建立了可解尺度流场与亚格子应力之间的数据映射模型,并对模型开展了先、后验测试.
先验测试结果表明,ANN 亚格子应力模型能够给出与DNS 高度吻合的亚格子应力,在不同滤波尺度及雷诺数上有较好的泛化能力.此外,ANN 模型在亚格子耗散等非建模量上也体现出良好的预测性能.该模型与基于DNS 数据直接获得的对应物理量相关系数大都在0.9 以上,与梯度模型及Smagorinsky 模型相比有大幅提高.在模型后验测试中,利用ANN 模型得到的流向平均速度剖面优于Smagorinsky 模型、梯度模型及ILES 方法.从脉动速度均方根剖面上,ANN 模型在预测湍流脉动的性能方面相对其它常用参数化模型没有明显提升.综上所述,较之于传统LES 模型,基于ANN 方法得到的亚格子应力模型在先、后验中预测能力均有不同程度的提升,兼具先验高相关和后验高精度的特点.尽管如此,ANN 模型在后验中的精度提升程度较为有限,并且随着LES 网格尺度的增大,ANN 模型同样出现一定程度的精度下降.
在后续研究工作中,拟深入探究ANN 模型后验表现不如先验的原因,期望得到一个在先、后验测试中均与DNS 结果高度吻合的ANN 模型.此外,使用更多能够反映湍流物理机理的输入以及提高模型的可解释性和模型后验计算效率也是值得研究的问题.
