高温后单向侧压作用下混凝土与钢筋黏结-滑移性能研究

2021-12-01杨海峰马仙娣肖建庄张天宝

工程力学 2021年12期

杨海峰，马仙娣，肖建庄，张宇，张天宝

(1.广西大学土木建筑工程学院，广西防灾减灾与工程安全重点实验室，广西，南宁 530004；2.同济大学土木工程学院，上海 200092)

随着建筑业的快速发展和城市人口密度的增大，建筑火灾隐患逐渐增大，火灾高温会给钢筋混凝土结构带来不同程度的损伤[1]，其中就包括混凝土与钢筋间黏结性能的退化[2]，直接降低了钢筋混凝土结构承载力，因此开展高温后钢筋-混凝土间黏结性能的研究有助于钢筋混凝土结构的灾后评估。目前，国内外学者针对高温后混凝土与钢筋的黏结-滑移性能研究已取得了不少成果，如Ergün等[3]、Shamseldein等[4]分别研究了钢筋的直径、类型、位置以及混凝土强度对高温后混凝土与钢筋间黏结-滑移性能的影响，提出了预测高温作用后黏结强度的简单表达式。实际工程中，钢筋混凝土构件如梁柱节点等受周围混凝土的侧向约束，因此部分学者开始关注混凝土与钢筋在多轴应力下的黏结性能。Xu等[5]和Li等[6]分别研究了常温环境中钢筋混凝土在不同侧拉、侧压以及多轴组合应力作用下的黏结-滑移，分析了侧向应力对峰值黏结应力和峰值滑移的影响规律，建立了多轴应力下的黏结-滑移曲线方程。尽管如此，高温后多轴应力状态下混凝土与钢筋间的黏结性能研究仍鲜见报道。为此，本文完成了48个高温后不同侧压作用下钢筋混凝土试件的中心拉拔试验，研究高温后单向侧压作用对混凝土与钢筋间的黏结-滑移性能影响，提出高温后侧压作用下的黏结强度理论，以期完善火灾后钢筋混凝土结构和构件的评估方法，为高温后混凝土与钢筋间的黏结理论研究提供参考。

1 试验概况

1.1 原材料与配合比设计

本试验的粗骨料(CA)来自南宁市武鸣区某石场，为粒径5 mm～31.5 mm的连续级配天然碎石骨料，表观密度2702.9 kg/m3，堆积密度1480.0 kg/m3，吸水率0.28%，压碎指标11.41%；细骨料(S)来自南宁市云桥建材市场，采用P·O 42.5 普通硅酸盐水泥(C)和城市自来水(W)；钢筋采用直径为20 mm的精轧螺纹钢筋PSB575，实测屈服强度684 MPa，弹性模量为200 GPa。参照规范《普通混凝土配合比设计规程》(JGJ 55−2011)并结合试配结果，最终采用的配合比如表1所示，表中fcu,20为常温状态下立方体抗压强度。

表1 混凝土配合比Table1 Mix proportion of concrete

1.2 试件设计及加载方案

本文以温度(T=20 ℃、300 ℃、400 ℃、500 ℃)和侧压力(p=0、0.1fcu,20、0.2 fcu,20、0.3 fcu,20)为变化参数设计16组中心拉拔试件，每组3个，共48个，试件尺寸如图1所示，钢筋-混凝土粘结段长度为100 mm。试件以温度-侧压力比的格式进行编号，如20-0.1代表20 ℃下侧压力比为0.1的试件。

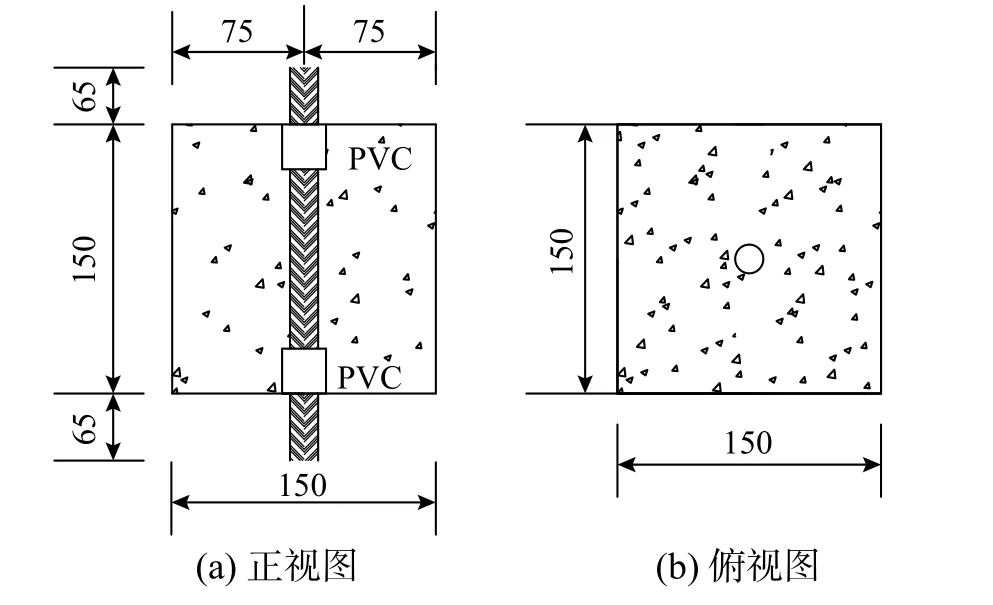
图1 试件尺寸 /mmFig.1 Specimens size

考虑到实际工程中建筑遭受高温后混凝土强度降低，但结构本身所承受的外部荷载不变，因此不同高温后试件施加的侧压力p相同，导致实际侧压力比p/fcu,T(fcu,T为经历高温T后的立方体抗压强度)随着高温后混凝土强度降低而发生变化，各温度下的实际侧压力比如表2所示。

表2 不同温度的侧压力比Table2 Lateral pressure ratio at different temperatures

高温试验采用结构大厅RX3-45-9工业电阻炉进行，见图2(a)。升温制度为仪器系统内置，对应目标温度300 ℃、400 ℃、500 ℃时分别记录下了如图2(b)所示的升温曲线，达到目标温度后再保持恒温6 h[7]。

图2 高温试验装置及升温曲线Fig.2 High temperature test device and heating curves

中心拉拔试验在可提供稳定侧压的高压伺服静动真三轴试验机(TAWZ-5000/3000)上完成。加载装置及受力简图如图3(a)、图3(b)所示，试验加载装置由高压伺服静动载真三轴试验机、中心拉拔反力架和侧压板组成。

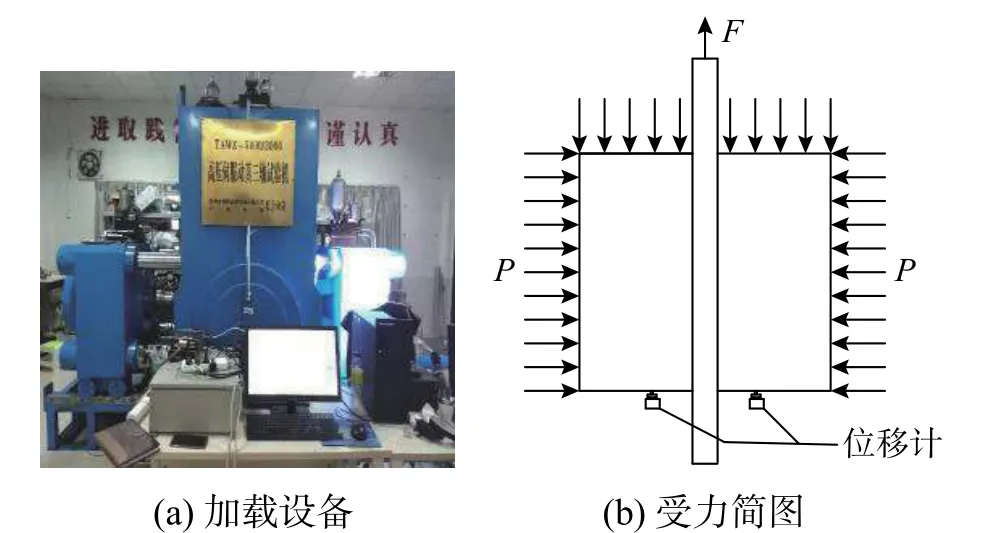
图3 侧压作用下中心拉拔试验Fig.3 Pull-out test under lateral pressure

中心拉拔荷载施加前，首先按力控方式对试件施加侧向压力至预定值，其次进行正式中心拉拔试验，加载方式采用位移控制，加载速度为0.5 mm/min，试件自由端滑移值采用2个外置位移计同步采集(如图3(b))。考虑到加载端滑移包含了钢筋的弹性拉伸和混凝土的压缩变形，为分析方便，后续仅使用自由端的位移数据进行分析。

2 试件破坏形态与实测曲线

试件破坏形态如图4所示。由试验结果及图4可知，高温后拉拔试件破坏形态主要与侧向压力和高温温度有关。

在无侧压下，由于没有侧向约束，试件出现劈裂破坏，混凝土试件随机被劈裂为2块～3块；在侧向力作用下，试件发生劈裂-拔出破坏，且裂缝垂直于侧压板方向，裂缝形态如图4(a)所示；如图4(b)的实际破坏图可知，随着侧向压力比从0.1增至0.3，试件破坏时表面产生的裂缝宽度明显减小。温度越高裂缝宽度越小，在20 ℃时，裂缝较为明显；随着温度的升高，试件表面的裂缝越来越小；当试件经历的最高温度为500 ℃时，试件表面没有明显裂缝，此时在侧压作用下破坏形式表现为拔出破坏(如图4(b))。随着温度升高，试件内部的破坏形态发生变化。当温度较低时，主要裂缝沿粗骨料发展；当温度较高时，主要裂缝沿砂浆和混凝土的界面发展，呈现一种被钢筋肋“刮出”的形态。出现上述现象的主要原因是：侧压比增加时，界面上混凝土的剪切性能可以充分发挥，试件发生延性破坏。随着温度升高，试件的劣化程度也越大，混凝土变得更“酥脆”，破坏发生在砂浆和粗骨料的界面上，因而混凝土从外观上看形态保持良好。

图4 试件破坏形态Fig.4 Failure patterns of specimens

高温后每组拉拔试件的平均黏结-滑移曲线如图5所示。图中τ表示平均黏结应力τ=F/(πdL)，其中：d为钢筋直径；F为拉拔力；L为粘结长度；s为钢筋自由段滑移量。结合图4、图5可知，在无侧压时曲线下降段较陡，试件表现为劈裂破坏，随侧压比的增加，试件发生劈裂-拔出破坏，曲线的下降段趋于平缓；随着温度升高，试件发生拔出破坏，下降段也趋于平缓。

图5 黏结-滑移全曲线Fig.5 Bond-slip curves

3 黏结-滑移特征值分析

为研究峰值黏结应力和峰值滑移特征值与温度及侧压力比的关系，定义峰值黏结应力为，峰值滑移为，残余黏结强度为实测黏结-滑移曲线下降段切线趋近水平时对应的黏结强度。统计每组3个试件特征值的平均值，得到如下特征值关系。

3.1 峰值黏结应力

高温后峰值黏结应力与侧压力比之间的关系如图6所示。由图可知，峰值黏结应力随着侧压力比值的增加而增大，20 ℃时，侧压力比p/fcu,T为0.1、0.2、0.3时比无侧压的峰值黏结应力分别提高了13%、25%、46%；300 ℃、400 ℃、500 ℃时，对应的数值分别提高了11%、58%、67%和48%、96%、125%以及103%、156%、164%。说明：随着高温温度增加，侧压力对峰值黏结应力的提高更为显著。这是因为，随着温度的升高，试件抗压强度明显下降，内部结构变得疏松，对钢筋的握裹力下降，施加侧压力后可以大幅增强混凝土-钢筋之间的机械咬合力和摩擦力。综合分析峰值黏结应力的变化规律，峰值黏结应力与温度和侧压比的关系可用式(1)描述：

图6 峰值黏结应力与侧压力比的关系Fig.6 Relationship between peak bond stress and lateral pressure ratio

3.2 峰值滑移

高温后不同侧压力比下试件的峰值滑移如表3所示。由表可知，在20 ℃、300 ℃时，峰值滑移整体随着侧压力比的增加而增大，结合表3及图5中黏结-滑移曲线可以看出，由于200 ℃、300 ℃时无侧压试件发生劈裂破坏，混凝土黏结强度瞬间下降，从而峰值滑移量较小。随着侧压力比增加，由于侧压力的存在，混凝土与钢筋肋之间的部分被剪坏后，混凝土与钢筋间的黏结力继而由摩擦力提供，故而滑移量有所增加。400 ℃时，试件400-0.00、400-0.15、400-0.30、400-0.45的峰值滑移分别为0.73 mm、0.97 mm、0.90 mm、1.01 mm，其中400-0.30试件的峰值滑移略有下降，可能为试验测试误差所致，说明随着侧压力增加，峰值滑移整体有所增加，但侧压力比大于0.15后，峰值滑移变化不明显。

表3 峰值滑移与侧压力比的关系Table3 Relation between peak slip and lateral pressure ratio

从表3中还可知，在500 ℃时，无侧压组的峰值滑移大于侧压组的峰值滑移，且侧压比0.2～0.6组的峰值滑移基本保持不变。可能原因是：混凝土受高温作用，内部结晶水蒸发和水泥砂浆的膨胀产生了大量了微裂缝，使得混凝土强度大幅降低。当施加侧压力时混凝土内部产生平行于侧压板方向的拉应力，这些拉应力使得混凝土内部的裂缝进一步开展，对混凝土造成了进一步的损伤。所以此时侧压力的作用不但不能使滑移值增加，反而使其减小，呈现在施加侧压力之后，峰值滑移较无侧压时减小且随侧压力的增加峰值滑移基本不变的现象。

3.3 残余黏结强度

图7 残余黏结强度与侧压力比的关系Fig.7 Relationship between residual bond strength and lateral pressure ratio

4 高温后黏结强度理论计算

4.1 黏结-滑移微观传力模型及肋前混凝土破坏准则

无侧压下混凝土与变形钢筋间发生破坏时的黏结-滑移传力模型如图8(a)所示[8]，图中的和μ表示高温后的挤压力和摩阻力，对图8(a)中肋前混凝土破坏面上的小微元A点进行受力分析可知，该点受到多向应力作用(图8(b))，其环向、径向应力σr、σθ、τ与主应力σ1、σ2、σ3之间的关系由文献[8]给出。

图8 黏结-滑移微观计算模型Fig.8 Micro calculation model of bond-slip

由于肋前混凝土承受多轴应力，本文选用文献[9]中建议的高温后混凝土多轴破坏拉压子午线方程与偏平面方程(式(2)、式(3))，其中：σ0、τ0分别为相对八面体正应力和剪应力(σ0=σoct/fc，τ0=τoct/fc，σoct、τoct为八面体正应力和剪应力)；θ为罗德角，θ与主应力间的关系及k1、k2、k3的取值均参照文献[9]确定。基于图8中的计算模型并利用文献[9]中高温后混凝土破坏准则计算得到变形钢筋肋前挤压力后，结合摩阻力µ关系并利用水平方向受力平衡方程，进而确定峰值黏结应力。

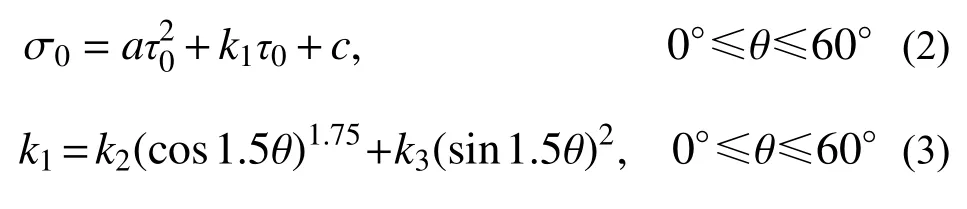
4.2 高温作用后无侧压时黏结强度计算

根据图8(a)可知，钢筋横肋挤压面积为π(d′+h)h/sinα，d′+2h为咬合齿任意计算点A处所在破坏面到变形钢筋基圆表面处的距离，在此状态下滑脱裂缝沿图8(a)模型中A点处所在平面发生破坏，荷载下降时形成峰值，此时咬合齿的计算面积为π(d′+2h)l，当达到极限状态时，发生劈裂破坏，根据几何关系设此时圆柱体的夹角γ=90◦−α−β (α为肋面倾角，取25°；β为钢筋与混凝土内裂缝的夹角，取β=52.5°)，则咬合齿的计算面积为π(d′+2h)lsinβ，对横肋作用面上的挤压力和摩擦力向齿根作用面投影可得到式(4)、式(5)，d为变形钢筋直径(本文中d=20 mm)，d′为变形钢筋基圆直径=0.94d，h为横肋高平均值=0.07d，l为横肋间距。

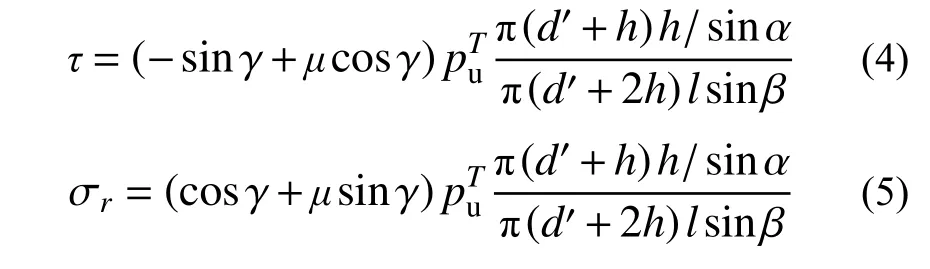
根据楔锥作用和环向应力假设[10]，由平均径向挤压力pr作用产生环向应力σθ得到式(6)、式(7)，式中：r为到圆心距离；kθ为环向应力系数，计算式如式(8)；c/d为相对保护层厚度(本文c/d=3.125)，根据文献[11]的实验数据，在20 ℃、300 ℃、400 ℃、500 ℃时钢筋-混凝土间的摩擦系数µ取值分别为0.518、0.541、0.561、0.582。

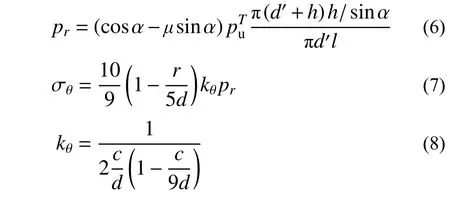
由式(4)～式(8)代入式(2)～式(3)可得到σr、σθ、τ值及相互关系，利用平衡条件以及σr、σθ、τ与的关系可得到此状态时所对应的挤压力。

为计算钢筋与混凝土间的黏结应力，将挤压力和摩阻力对变形钢筋产生的作用力向水平方向投影，即可得到如式(9)所示的混凝土与钢筋间的极限黏结强度表达式，将通过上述计算所得到的挤压力pTu代入式(9)即可得到极限应力状态下的峰值黏结应力计算值τTe。

4.3 高温作用后单向侧压作用时的黏结强度计算

侧向压力作用下的计算模型如图9所示，该模型将混凝土简化为开孔板，钢筋简化为小圆板。受侧压下混凝土平板和钢筋圆板模型的应力函数参考文献[12]。

图9 单向侧压力作用下的力学计算模型Fig.9 Mechanical calculation model under uniaxial lateral pressures

定义高温后混凝土中心拉拔试件在受到侧压作用时，混凝土内部产生的径向力、环向力、切向力分别为σρ、σφ、τρφ，侧向压力q对变形钢筋与高温后混凝土内部破坏面的应力(σr、σθ、τ)状态产生影响，为简化计算，假设肋前混凝土挤压力和侧向压力产生线性叠加作用，其余假设同文献[12]。对应力场函数沿界面进行积分计算得到如下所示的径向、环向平均应力表达式(切线应力积分结果为0)：

式中，k =Ec/Es(Ec、Es分别为混凝土弹性模量和钢筋弹性模量)，根据文献[13 −14]结果，在300 ℃、400 ℃、500 ℃时混凝土弹性模量分别取0.85 Ec20、0.90 Ec20、0.75 Ec20，其中： Ec20为常温下混凝土弹性模量；νc和νs分别取0.25和0.3；r和φ值的定义如计算模型所示，r=10 mm。

由于施加侧压力前后的传力模型相似，根据叠加原理对σr和σθ表达式进行修正，式(5)增加ρ=d′/2+h 处的径向平均应力计算值 σ¯ρ，得到拔出状态时的环向压力如式(12)：