基于BP神经网络的RC框架结构地震易损性曲面分析：考虑地震动强度和持时的影响

程诗焱，韩建平，于晓辉，吕大刚

(1.兰州理工大学甘肃省土木工程防灾减灾重点实验室，兰州 730050；2.兰州理工大学防震减灾研究所，兰州 730050；3.哈尔滨工业大学结构工程灾变与控制教育部重点实验室，哈尔滨 150090；4.哈尔滨工业大学土木工程学院智能防灾减灾工业与信息化部重点实验室，哈尔滨 150090)

已有研究表明：持时对结构损伤的影响显著[1−2]。Chandramohan等[3]、Raghunandan等[4]的研究表明，地震动持时会加速结构损伤的发展，降低结构滞回耗能能力，增加了结构倒塌的风险。韩建平等[5]和孙小云等[6−8]的研究表明，具有较长持时特性的地震动会使混凝土框架结构的节点发生严重破坏。基于上述研究，在结构抗震分析时忽略地震动持时的影响很可能会导致由地震动持时特性引起的明显结构抗震设计与评估结果偏差，使处于活跃的俯冲地震带(该区域常发生具有较长持时特性的地震事件)附近的结构具有低于预期的安全裕度。因此，需要进一步讨论如何在结构损伤分析中明确考虑地震动持时特性。

地震易损性分析能够量化结构系统的安全裕度，并全面地描述地震事件与结构中存在的不确定性，是基于性能地震工程的重要环节之一。于晓辉等[9]提出了条带-云图易损性分析方法，用于提高传统云图法的运算能力。Baker[10]分别针对云图、IDA和条带法提出了向量型易损性分析方法，在谱加速度的基础上进一步引入了谱型参数。尽管目前已有很多关于易损性方法的讨论及应用[11−17]，但涉及的分析方法都要求数据具有较好的稳定性，而具有离散性的持时数据则无法使用这些方法建立可靠概率模型，故无法将地震动持时特性定量地考虑到易损性分析中。

近年来，人工神经网络开始得到了地震工程研究人员的关注。Mitropoulou等[18]、Wang等[19]使用人工神经网络(artificial neural networks,ANN)建立了地震动强度指标(intensity measure,IM)与结构 损 伤 指 标(damage measure,DM)的 关 系。Papadrakakis等[20]提出了基于ANN的蒙特卡洛模拟方法，用于大型混凝土大坝的易损性评估。人工神经网络可以进行基于大样本的数据分析，为进一步在易损性分析中考虑地震动持时特性提供了思路。

综上，本文提出了一种基于BP(back propagation)神经网络的地震易损性分析方法，该方法可以合理考虑地震动持时特性的影响，获得同时包含地震动持时参数与地震动强度参数信息的地震易损性曲面。分别选用2组具有长、短持时特性的地震动记录作为输入，以5层、8层、10层钢筋混凝土框架结构作为研究对象，使用BP神经网络建立地震动强度、持时与结构响应间的相关关系并进行结构易损性分析，获得了不同损伤水平下的地震易损性曲面。进而以此为基础，对分析方法的有效性进行了讨论。

1 考虑地震动持时的地震动记录选取

地震动持时的定义较多，包括重要持时(Ds)、括号持时(Db)、一致持时(Du)及有效持时等。对于同一条地震动记录而言，其调幅前后的Db和Du值并不唯一，这会进一步增加地震动持时的不确定性[2]。相比之下，基于Arias强度[21]的重要持时仅表示地震动加速度时程的累积能量，地震动加速度幅值对其影响可忽略不计，具有较好的鲁棒性[3]。同时，5%～75%重要持时( Ds5-75)在地震工程的研究中应用更为广泛[3]。

依据文献[3]的研究结果，本文选用 Ds5-75作为地震动持时指标，使用条件平均谱(conditional mean spectrum,CMS)为目标谱，结合地震动持时特性，从PEER NGA-West2、USGS工程强震数据中 心(Center for Engineering Strong Motion Data，US Geological Survey)、日本NIED强震动观测台网(Strong-motion Seismograph Networks，National Research Institute for Earth Science and Disaster Prevention)、汶川地震动数据库以及墨西哥地震动数据库中挑选地震动记录[3]。CMS的构建方法参见文献[3,22]。

文献[3]收集了全球强震的2000组水平分量地震动记录，建立了所有记录的 Ds5-75直方分布图并综合分析，建议若地震动记录两个水平分量中至少有一个分量的 Ds5-75大于25 s则认定为长持时地震动记录。采用单个分量的 Ds5-75而不是两个分量 Ds5-75的几何平均，是因为这样做会把一些可行的长持时记录过滤掉。阈值的选取既要考虑持时要长到可以观察其影响，但也不能太长以致于可选的长持时地震动记录数量太少。本文借鉴这一建议，选用25 s作为界定长、短持时地震动记录的阈值。

由于地震动幅值和频谱特性会增加易损性分析结果的不确定性，因此本文对2组地震动记录进行了谱匹配[3]，以确保每条长持时地震动记录有与其谱型、频率相匹配的短持时地震动记录。该处理方法、误差控制以及调整系数详见文献[3]。

最终选取140条具有长持时特性的地震动记录和140条具有短持时特性的地震动记录，地震动信息详见文献[23]。谱匹配后两组地震动记录的反应谱如图1所示，地震动记录的 Ds5-75分布如图2所示。

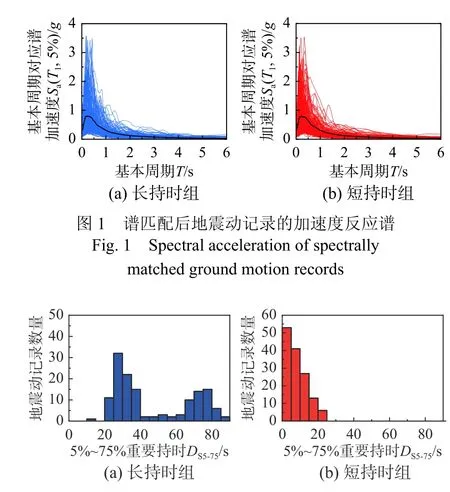
图2 谱匹配后地震动记录的Ds5-75分布Fig.2 Ds5-75 distribution of spectrally matched ground motion records

2 RC框架结构的设计及建模

本文选取5层、8层、10层RC框架结构为研究对象[24]。5层RC框架结构设防烈度为7度，基本设计加速度为0.15 g；8层RC框架结设防烈度为8度，基本设计加速度为0.2 g，10层RC框架结构设防烈度为8度，基本设计加速度为0.2 g。三个结构采用相同的设计基本资料：基本风压0.4 kN/m2；地面粗糙度C类；基本雪压0.30 kN/m2；标准层活荷载2.0 kN/m2；标准层恒荷载4.5 kN/m2；屋面为不上人屋面，楼板厚120 mm，屋面恒荷载为7.0 kN/m2；设计地震动分组为第1组，II类设计场地，场地特征周期为0.35 s。

梁、柱钢筋选用HRB335，箍筋选用HPB235；5层结构选用C30混凝土，8层结构选用C35混凝土，10层结构选用C35混凝土。三个结构的平面布置形式相同，选取2号轴线对应的一榀框架作为分析对象。结构平、立面布置如图3所示。结构主要梁柱配筋如图4所示，图中5KZ表示5层结构框架柱，5KL1表示5层结构1号框架梁，5KL2表示5层结构2号框架梁，其余编号依此类推。

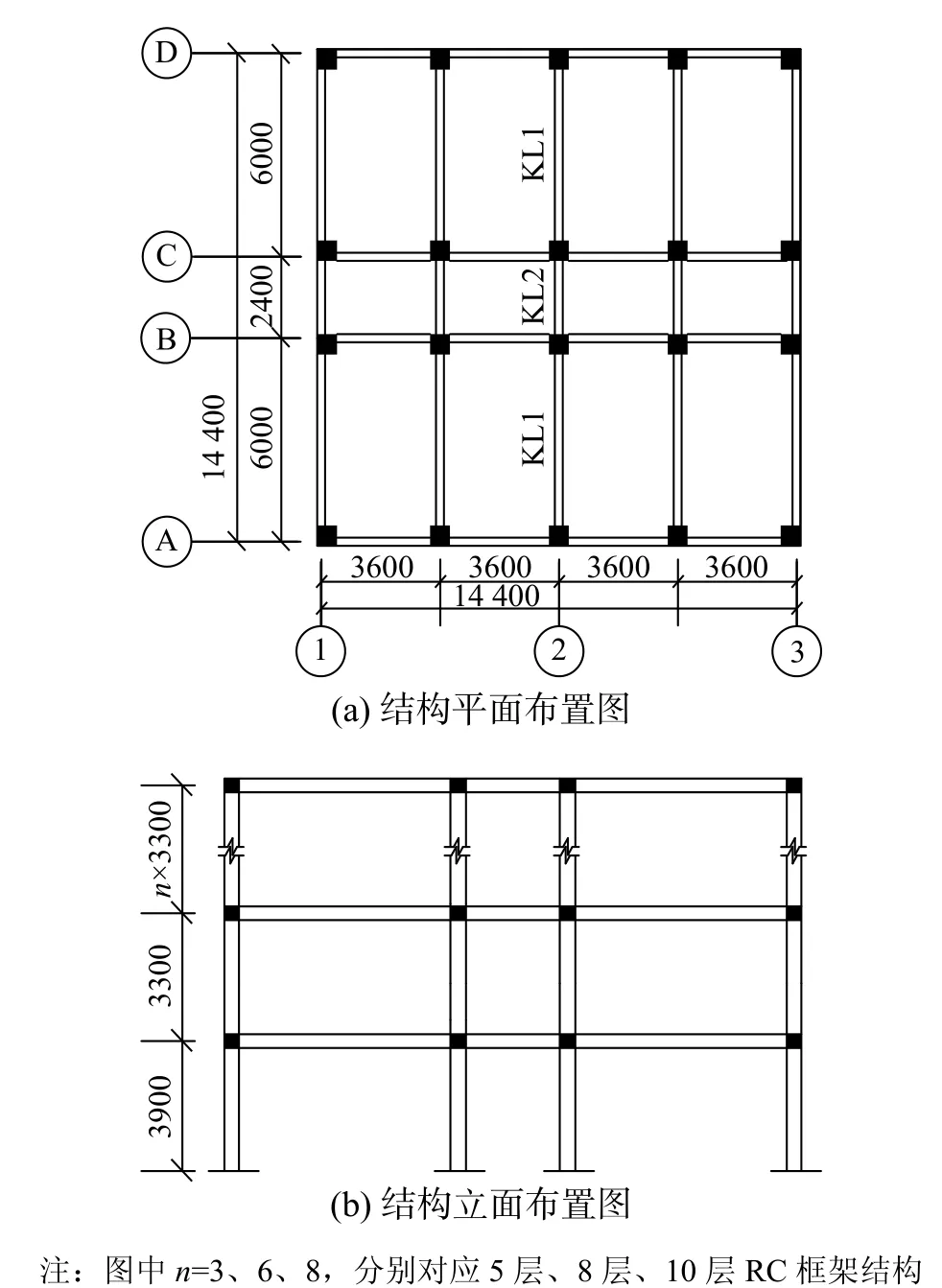
图3 算例结构的平面及立面布置图Fig.3 Plan and elevation view of study cases

图4 梁、柱截面配筋图Fig.4 Reinforcement details of typical beams and columns

使用OpenSees作为分析平台构建结构有限元模型，选取梁、柱作为结构的基本单元，并采用杆系模型模拟梁、柱单元。建模基本原则为：1)考虑梁-柱节点为固接，无特殊定义；2)使用Concrete01材料模型模拟混凝土材料，考虑箍筋对核心区混凝土的约束效应，不考虑混凝土受拉情况；3)使用Steel02材料模型模拟钢筋；4)考虑了柱单元因自重引起的P-Δ效应；5)使用非线性梁柱单元模拟结构非倒塌破坏。

3 基于BP神经网络的地震易损性分析

向量型IM可以提供更多地震动信息，从而提高结构损伤分析结果的准确性，降低因忽略地震动特性引起的结果偏差。故本文使用向量型IM(IM=[IM1,IM2])进行易损性分析，其中IM1为主参数，IM2为第二参数。

3.1 传统的基于向量型IM的地震易损性分析方法

对于条带法，传统的基于向量型IM的易损性分析是以IM1=im1为条件，将IM2作为预测变量进行条件概率分析，即使用逻辑回归计算结构倒塌概率，通过线性回归建立非倒塌结构响应预测模型[10]。倒塌概率模型如式(1)所示：

式中：a、b为经逻辑回归分析得到的系数，受IM1变化的影响；C为指示变量，0表示结构未倒塌，1表示结构发生倒塌。

传统方法使用线性回归的方法将IM2引入结构损伤分析[10]。对IM1=im1条带，建立IM2与结构损伤需求D的关系：

式中：c、z为系数；e为残差。

需要注意的是，上述参数需要随IM1的变化重新估算。在此基础上，结构非倒塌状态的条件超越概率可表示为：

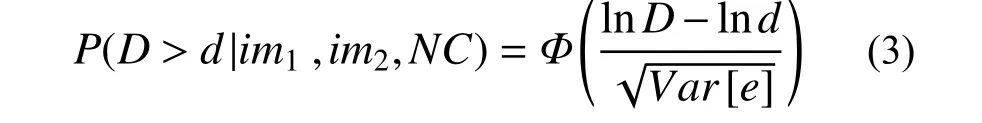
式中：d表示结构损伤水平；Φ()表示标准正态分布。

这一方法要求数据具有较好的稳定性，离散性较大的数据无法使用该方法建立可靠的线性回归模型。

3.2 基于BP神经网络的地震易损性分析方法

BP神经网络通过寻找输入与输出间的最佳关系建立网络模型，其数学意义及算法步骤明确，被广泛应用于概率统计分析领域。研究使用BP神经网络建立IM与结构损伤需求D的关系模型，为便于表述，记在IM1=im1，IM2=im2条件下网络模型的输出为 DANN,i|im1,im2。

基于BP神经网络的地震易损性函数为：

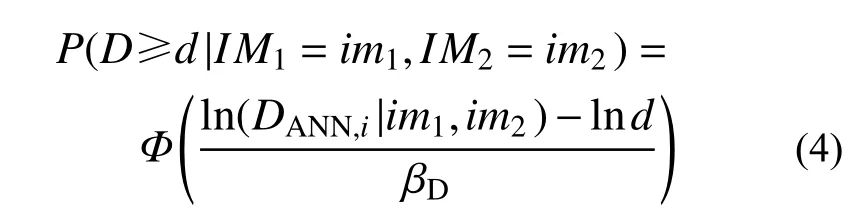
式 中： P(D≥d|IM1=im1,IM2=im2)表 示 引 起d损伤水平的条件超越概率；βD表示对数标准差，其表达式为：式中：Di表示当IM1=im1、IM2=im2时的结构损伤需求参数；N表示输入的地震动记录的数量。

本文使用逻辑回归计算了算例结构的倒塌概率：

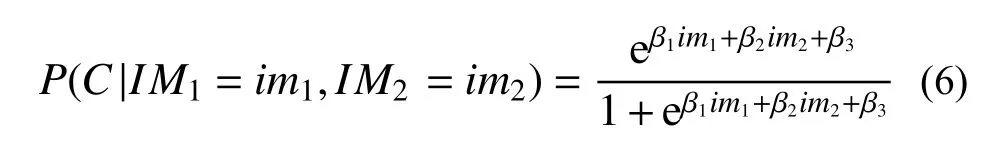
式中，β1、β2和β3是对统计结果进行逻辑回归分析得到的相关系数。

依据全概率定理对式(4)进行了倒塌修正[25]，考虑倒塌概率的易损性函数模型如下：

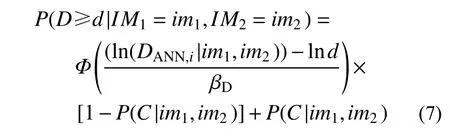
3.3 方法对比

由于结构基本周期T1对应谱加速度Sa(T1,5%)在工程领域应用广泛[10]，且具有很好的有效性及充分性[26]，故选择Sa(T1,5%)作为主参数IM1。5层、8层和10层RC框架结构的T1分别为0.774 s、1.187 s和1.460 s。

重要持时仅表示时间，不反映地震动记录的强度且具有不可预测性，因此很难建立Ds5-75与D的相关关系。此外，Riddell[27]的研究表明与能量相关的强度指标可用于反映持时特性，故本文选择均方根加速度arms[28]作为第二参数IM2。综上，使用IM=[Sa(T1,5%),arms]作为地震动强度指标，其中arms为：

式中：a(t)为时刻 t 的地震动加速度；t1和t2分别为强震段始、末时刻。

易损性分析中，强度指标与结构损伤需求的关系模型决定了分析结果的准确性，也是区别不同分析方法的标志之一。本节通过对比两种方法构建的关系模型进一步讨论BP神经网络在易损性分析中的应用，使用的数据均源自文献[2]。限于篇幅，在此列出8层结构 Sa(T1,5%)=0.29 g、Sa(T1,5%)=0.67 g和Sa(T1,5%)=0.91 g条带下[2]的对数线性回归结果，如图5～图7所示。

图5 8层结构 Sa(T1,5%)=0.29 g条带线性回归结果Fig.5 Linear regression results of 8-story structure of Sa(T1,5%)=0.29 g

图6 8层结构Sa(T1,5%)=0.67 g条带线性回归结果Fig.6 Linear regression results of 8-story structure of Sa(T1,5%)=0.67 g

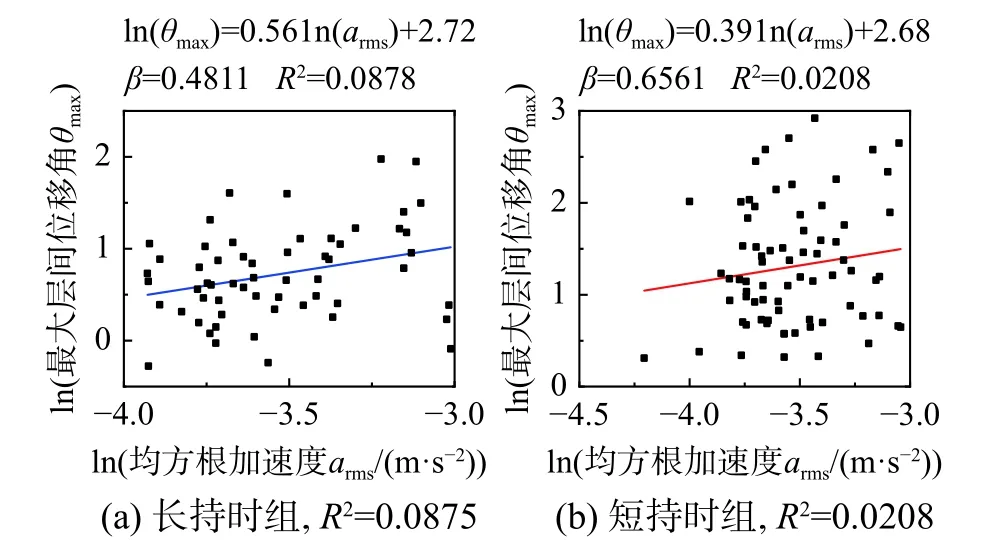
图7 8层结构Sa(T1,5%)=0.91 g条带线性回归结果Fig.7 Linear regression results of 8-story structure of Sa(T1,5%)=0.91 g

关于BP神经网络，Karsoliya[29]的研究表明，1层～2层隐含层足以解决工程中复杂的非线性问题，对精度要求高的网络可设3层隐含层，但不建议使用4层隐含层，因其会导致网络发生局部最优的问题。目前仍未有普适的方法确定隐含层及其神经元数量，因为这些参数不仅受到输入层、输出层的影响，激活函数的复杂程度、神经网络的架构、训练算法和训练样本都会影响参数的选择[29]。研究[29−30]建议在满足精度要求的前提下取最简单的网络结构，经调试确定网络参数。基于上述研究理论及网络调试结果，本文建立了3层(即含一个隐含层)神经网络，网络模型参数如下：

1)输入层含2个神经元，输出层含1个神经元，隐含层含3个神经元；

2)最大迭代步数为1000步；

3)学习速率设置为0.005；

4)误差容许值为0.001；

5)动量常数设置为0.5。

由图8～图9可知，8层结构BP网络模型R值为0.8995～0.9321，而传统方法的R2为0.0208～0.1038。通过对比可知，传统方法建立的模型的精度远低于BP神经网络的模型精度，其并不总能建立理想的关系模型。该方法要求数据具有较好的稳定性，也因此限制了在易损性分析中考虑持时特性。而BP神经网在回归分析中表现良好，建立的关系模型可靠，为考虑持时特性的损伤分析提供了可行方案。

图8 长持时地震动输入下，8层结构BP神经网络模型回归结果Fig.8 BP network model regression results of 8-story structure under long-duration ground motion

图9 短持时地震动输入下，8层结构BP神经网络模型回归结果Fig.9 BP network model regression results of 8-story structure under short-duration ground motion

4 地震易损性分析

基于文献[2]的数据进行易损性分析，选取最大层间位移角θmax作为损伤指标，依据FEMA273/356[31−32]确定了立即居住(IO)、生命安全(LS)和倒塌预防(CP)的极限状态定义值，采用条带法进行结构时程分析。其余详细信息及结构响应、极限状态和持时关系的讨论详见文献[2,33]。

基于3.2节理论，计算了长、短持时地震动输入下三个结构不同极限状态的易损性曲面，分别如图10～图15所示。由图10～图15可见，同一损伤水平下，各结构长、短持时地震动输入下易损性曲面的形态差异显著。

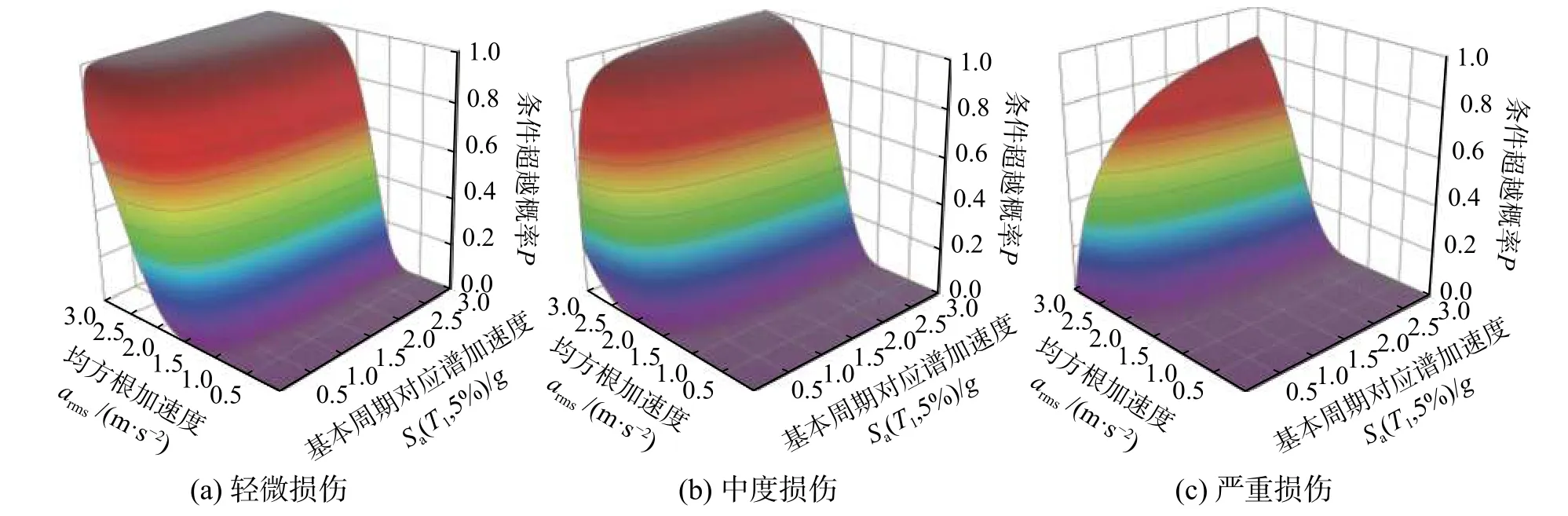
图10 长持时地震动输入下，5层结构易损性曲面Fig.10 Fragility surfaces of 5-story structure under long-duration ground motions

图11 短持时地震动输入下，5层结构易损性曲面Fig.11 Fragility surfaces of 5-story structure under short-duration ground motions

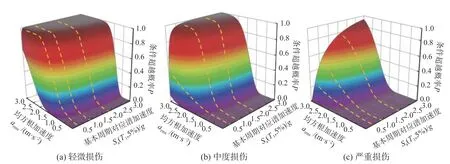
图12 长持时地震动输入下，8层结构易损性曲面Fig.12 Fragility surfaces of 8-story structure under long-duration ground motions

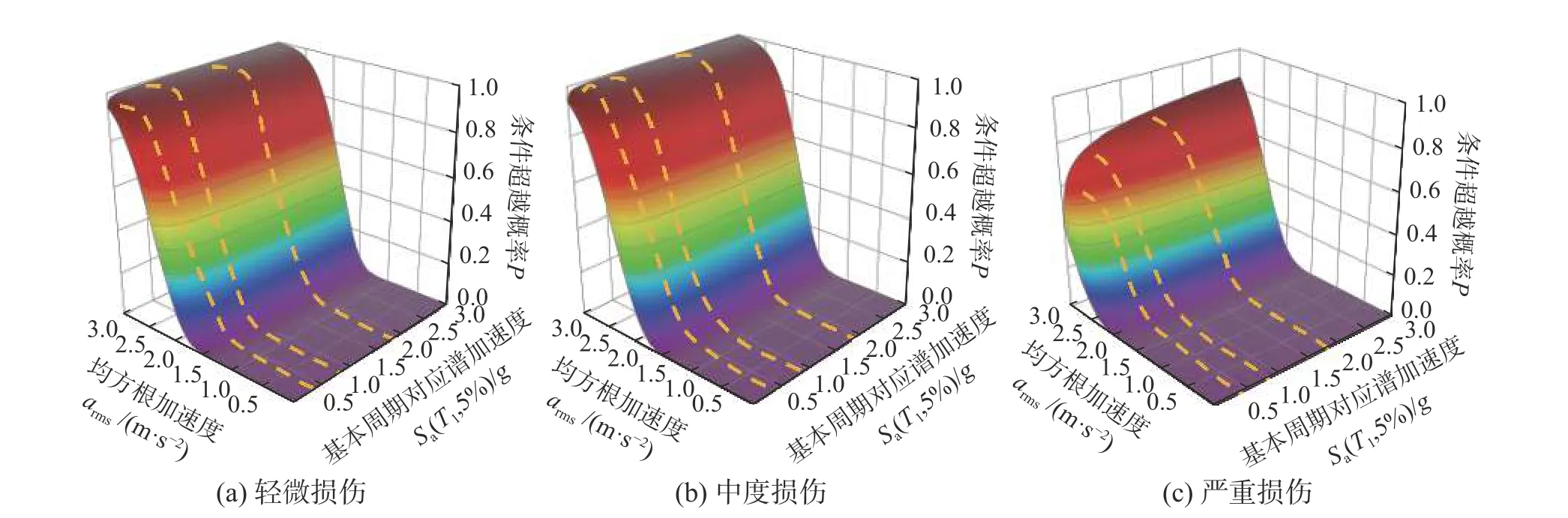
图13 短持时地震动输入下，8层结构易损性曲面Fig.13 Fragility surfaces of 8-story structure under short-duration ground motions

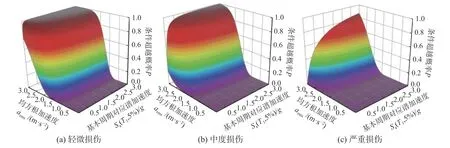
图14 长持时地震动输入下，10层结构易损性曲面Fig.14 Fragility surfaces of 10-story structure under long-duration ground motions

图15 短持时地震动输入下，10层结构易损性曲面Fig.15 Fragility surfaces of 10-story structure under short-duration ground motions

以8层结构为例，进行具体分析。图16、图17分别为图12、图13易损性曲面在arms-条件超越概率平面的投影曲线，长、短持时概率曲线的整体发展趋势差异显著。图中短持时地震动输入下得到的条件超越概率曲线的分布集中，不同Sa(T1,5%)条件下的损伤概率变化幅度平缓。与此相比，长持时地震动输入下得到的条件超越概率曲线的分布则较为分散，不同Sa(T1,5%)条件下的损伤概率变化幅度大。这是因为长持时地震动对结构损伤的影响与地震动强度水平正相关。即当Sa(T1,5%)增长到一定水平后，相比于短持时地震动，长持时特性会加剧结构损伤的发展，结构损伤风险也较之前有所提高，但在此之前结构的损伤程度由地震动强度水平控制。这一结果与前期研究结论一致[2,33]，可见BP神经网络能够抓取持时对结构响应的影响，建立IM与D的可靠回归模型，据其得到的分析结果是可信的。

图16 长持时地震动输入下，8层结构易损性曲线Fig.16 Fragility curves of 8-story structure under long-duration ground motions

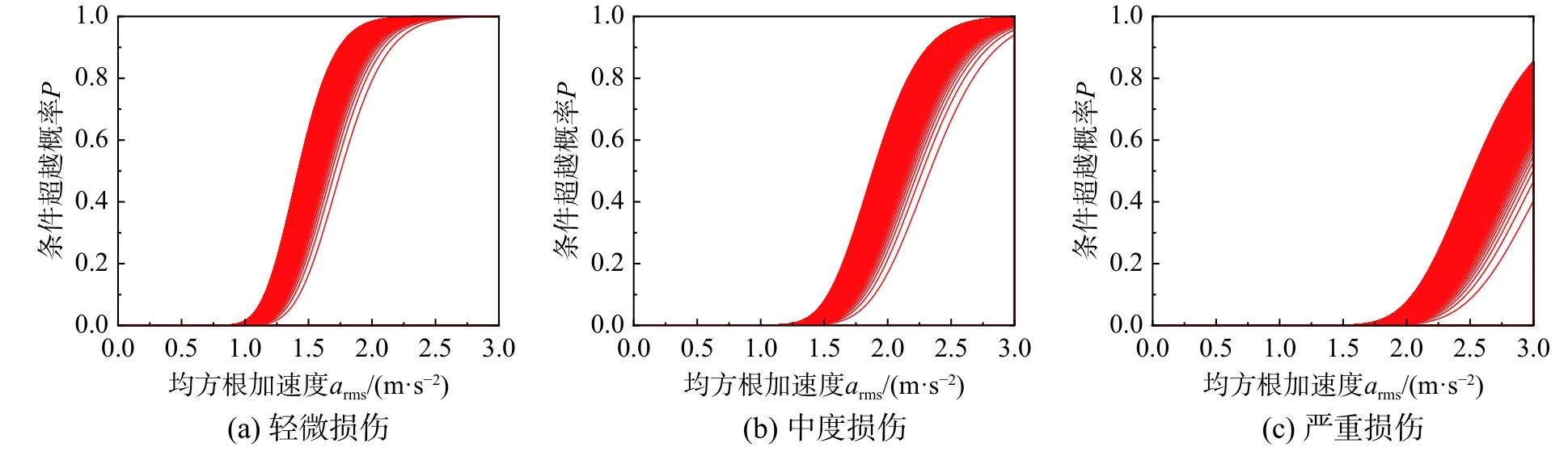
图17 短持时地震动输入下，8层结构易损性曲线Fig.17 Fragility curves of 8-story structure under short-duration ground motion

对8层结构，分别选取Sa(T1,5%)=0.2 g、Sa(T1,5%)=0.7 g和Sa(T1,5%)=1.7 g(图12～图13所 示虚线处的数据)条件下的易损性曲线进行进一步讨论，如图18(a)、图18(b)和图18(c)所示。当Sa(T1,5%)=0.2 g时，对应于三种损伤状态，短持时曲线明显高于长持时曲线，此时无论arms取何值，持时对结构损伤的影响都可忽略不计。当Sa(T1,5%)=0.7 g时，长持时地震动作用下的条件超越概率有不同程度的提高。当Sa(T1,5%)=1.7 g时，对应于三种损伤状态，长持时地震动输入下的条件超越概率基本均大于短持时地震动输入下的条件超越概率。当结构进入非线性阶段，在相同的地震动强度下，长持时地震动会引发更大的结构变形，结构损伤风险也相应提高。上述分析结果与前期研究结果一致[2]，即当地震动强度达到一定水平后，长持时地震动会使结构发生更严重的破坏。

图18 不同Sa(T1,5%)时长、短持时地震动输入下8层结构易损性曲线Fig.18 Comparison of fragility curves of 8-story structure under long-and short-duration ground motions with different Sa(T1,5%)values

5 结论

本文提出了基于BP神经网络进行易损性分析的方法，该方法易于操作允许使用向量型强度指标作为参数，综合考虑多种地震动特性。研究结果表明：

(1)BP神经网络可以综合考虑地震动强度、持时特性对结构损伤风险的影响，建立可靠的相关关系。引入arms后，数据离散性增大，此时传统方法无法建立可靠的关系模型，亦无法得到可信的损伤分析结果。相比之下，BP神经网络模型在回归分析中表现良好，使用该方法得到的易损性曲面的变化趋势及规律与前期关于持时影响的研究结果一致，其较好的模型精度确保了损伤分析结果的可信度，具有工程应用价值。

(2)持时对结构损伤的影响与地震动强度水平有关。只有当地震动强度达到一定水平时，才可在结构时程分析中观察到持时的影响，因此研究中应选取具有足够强度水平的地震动作为输入进行结构时程分析。