电网电压前馈控制VSG的阻抗建模与并网稳定性分析

2021-12-01杨伊茜陈杰万雨朦章新颖王开春

电力工程技术 2021年6期

杨伊茜，陈杰，万雨朦，章新颖，王开春

(1.南京航空航天大学自动化学院,江苏南京 211106；2.北京精密机电控制设备研究所，北京 100076)

0 引言

随着分布式电源在电力系统中渗透率的不断提高，传统电网将逐步发展成为电力电子变换装置占主导的低惯性、欠阻尼网络，电网调频调压难度增加，系统稳定性受到影响[1—2]。为解决上述问题，国内外学者提出了虚拟同步发电机(virtual synchronous generator,VSG)技术[3—6]，通过对电力电子并网装置施以特定的控制，模拟同步发电机(synchronous generator,SG)的外特性。

目前，针对VSG的虚拟惯量控制[4,6]、有功无功功率支撑[7]、小信号建模[8—10]、参数优化设计[10—11]等已开展了卓有成效的研究，但鲜有研究涉及电网含背景谐波的非理想条件下VSG对系统鲁棒性的影响。

针对背景谐波条件下的控制策略，如多谐振补偿器[12—15]、超前校正环节[16]、电网电压前馈控制[17—18]等已有诸多报道。文献[17]研究了LCL型逆变器的电网电压前馈方案，指出其可以有效降低电网电压引起的电流谐波；文献[18]从虚拟阻抗角度进行分析，指出前馈控制可以改变逆变器外阻抗特性，从而改善并网稳定性。但是上述文献仅针对常规电流控制型并网逆变器，并未涉及VSG技术。同时，为了推动VSG在分布式电网中的应用，国内外学者对VSG与电网之间的交互规律展开研究。文献[19—20]对比分析了电压控制型VSG与传统电流源型逆变器、电流控制型VSG的阻抗特性，发现电压控制型VSG的输出阻抗在中低频段呈感性，与电网交互时具有更加稳定的特性；但在高频段呈容性，并网时存在谐波振荡的风险。

针对以上问题，文中提出了一种基于电流环的VSG电网电压前馈控制。首先，分析了VSG工作原理及前馈函数的设计原则，采用谐波线性化方法，推导有、无电网电压前馈控制的VSG输出阻抗模型。然后，研究VSG在不同频段下的阻抗特性与各控制环节的关系，发现电网电压前馈控制可以有效抑制VSG接入电网时的谐波振荡，提高系统稳定性。最后，通过仿真和实验验证了阻抗模型以及相关分析的正确性。

1 VSG的电网电压前馈控制

1.1 VSG拓扑结构

图1为VSG的主电路拓扑及控制框图。其中，Vdc为逆变器直流侧电压；Sa1，Sb1，Sc1，Sa2，Sb2，Sc2为开关管控制信号；eabc为逆变器三相桥臂输出电压；ila，ilb,ilc为电感电流；voa，vob，voc为输出端电压；iga，igb，igc为三相并网电流；vga，vgb，vgc为电网电压；Lf，rl分别为滤波电感及其寄生电阻；Cf，rc分别为滤波电容及阻尼电阻；Zg为电网等效阻抗；Pset，Qset分别为给定有功功率和给定无功功率；PCC为公共连接点。

图1 VSG主电路拓扑及控制框图Fig.1 Main circuit topology and control diagram of VSG

根据瞬时功率理论可以计算得到有功和无功功率的表达式：

(1)

式中：iα，iβ分别为αβ坐标系下VSG的输出电流；vα，vβ分别为αβ坐标系下VSG的输出电压；Pe，Qe分别为实际输出有功功率和无功功率。

VSG的有功环路模拟SG机械特性，引入虚拟惯量，具备惯量调节和一次调频功能；无功环路模拟SG电磁特性，具备一次调压功能。两者的控制方程如下：

θ(s)=(Tset-Te+Dpωr)/[s(Js+Dp)]

(2)

Em(s)=[Qset-Qe+Dq(Vr-Vm)]/(Ks)

(3)

式中：s为复变量；J为虚拟转动惯量；Dp为阻尼系数；ωr为电网额定角频率；Tset，Te分别为给定转矩和电磁转矩，其中Tset=Pset/ωr，Te=Pe/ω≈Pe/ωr；θ为VSG输出电压调制波的相位；K为励磁调节器积分系数；Dq为调压系数；Vr，Vm分别为给定电压幅值和VSG输出电压幅值；Em为励磁内电势幅值，即VSG输出电压调制波的幅值。

有功、无功环路分别输出相位信号θ和幅值信号Em，两者构造得到VSG的桥臂电压eabc，作为空间矢量脉宽调制(space vector pulse width modulation，SVPWM)的调制信号：

(4)

VSG的滤波电感相当于SG的定子绕组，桥臂电压相当于内电势，且与电网电压之间存在一定的相角差φ，其中φ=arcsin[2ωrLfPset/(3EmVr)]。

1.2 电网电压前馈控制

图2为具有电网电压前馈控制的VSG结构框图，电网电压前馈点设置在电流控制器前后[21—22]。为便于分析，下文将该控制称为带前馈控制。

图2 VSG带前馈控制结构框图Fig.2 Block diagram of VSG with feedforward control

根据图2可进一步推导出等效控制框图，如图3所示，其中ic为电容电流；Kpwm为逆变器的输出调制比，可做归一化处理；GPI(s)为电流调节器；G1(s)，G2(s)为电网电压前馈函数。

根据图3，可以推导得到并网电流的表达式：

图3 VSG带前馈控制等效结构框图Fig.3 Equivalent block diagram of VSG with feedforward control

ig=GPI(s)iref/(sLf+rl+GPI(s))+G′(s)vg

(5)

其中：

G′(s)={[G1(s)(sCfrc+1)-sCf]GPI(s)+
[G2(s)(sCfrc+1)-(CfLfs2+
sCf(rc+r1)+1)]}/
[(sLf+rl+GPI(s))(sCfrc+1)]

(6)

由式(5)可知，VSG的输出电流不仅受电流环指令iref控制，还与电网电压vg相关。当G′(s)=0时，可得前馈函数G1(s)和G2(s)，如式(7)所示，此时ig与vg无关，消除了电网电压背景谐波对并网电流的影响。

(7)

2 正负序阻抗建模及分析

2.1 序阻抗模型推导

利用谐波线性化和对称分量法对VSG的正、负序输出阻抗模型进行推导。

在三相并网逆变器的并网端注入fp频次正序小信号扰动后，以A相为例，VSG的并网电压和并网电流为：

vga(t)=V1cos(2πf1t)+Vpcos(2πfpt+φv,p)

(8)

iga(t)=I1cos(2πf1t+φi,1)+Ipcos(2πfpt+φi,p)

(9)

式中：V1，Vp分别为基波电压和正序扰动电压的峰值；I1，Ip分别为基波电流和正序扰动电流的峰值；f1，fp分别为基频和正序扰动频率；φv,p为正序扰动电压初相角；φi,1，φi,p分别为基波电流和正序扰动电流的初相角。

对并网电压和并网电流进行坐标变换，得到其频域表达式：

(10)

(11)

(12)

(13)

其中：

(14)

(15)

将式(10)—式(13)代入式(1)，并忽略高次非线性小信号量，得到有功和无功功率在频域的表达式：

(16)

(17)

其中，上标“*”表示复数的共轭。

将式(16)和式(17)分别代入式(2)和式(3)，忽略二次项小信号量，得θ和Em在频域的表达式：

(18)

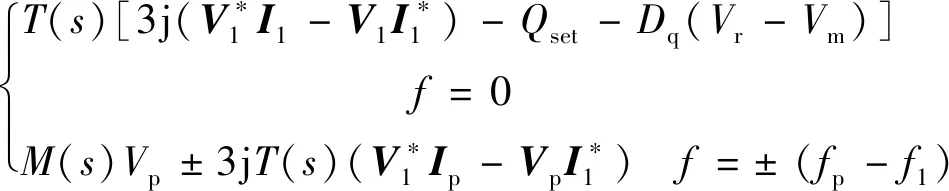
(19)

其中：

(20)

对式(4)的A相进行小信号分析，有：

(21)

(22)

将式(18)和式(19)代入式(22)，可得到fp频次下A相电压调制小信号，见式(23)。

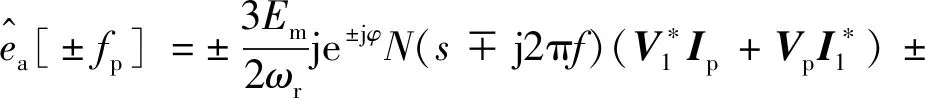
(23)

当VSG星型连接且对称运行时，VSG输出阻抗可用电压扰动及其激励产生的电流响应计算得到。A相电流响应等效电路如图4所示。

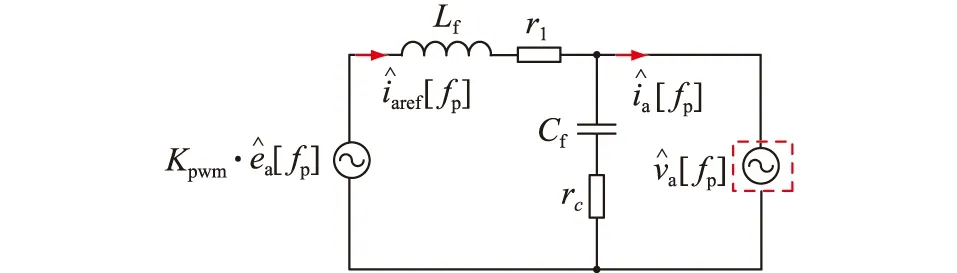
图4 fp频次下A相电流响应等效电路Fig.4 Equivalent circuit of A phase current response at fp

(24)

经图3前馈控制后的A相输出电压调制波为式(25)。再结合图4，得到具有电网电压前馈控制VSG的正序输出阻抗模型，如式(26)所示，同理计算得到并网端注入fn频次负序小信号扰动的负序阻抗模型，如式(27)所示。为便于比较，同时推导出了无电网电压前馈的VSG正负序输出阻抗模型，见式(28)和式(29)。

(25)

(26)

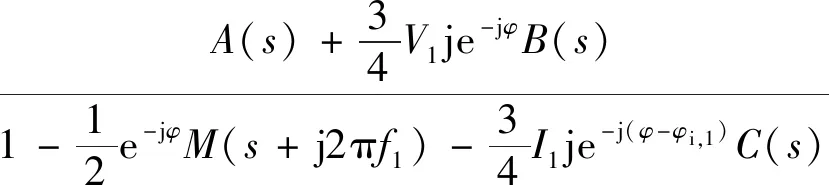
(27)

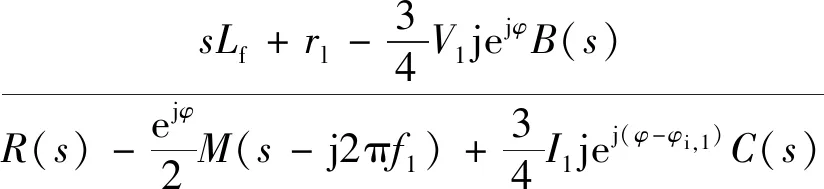
(28)

(29)

其中：

GPI(s)=kp+ki/s

(30)

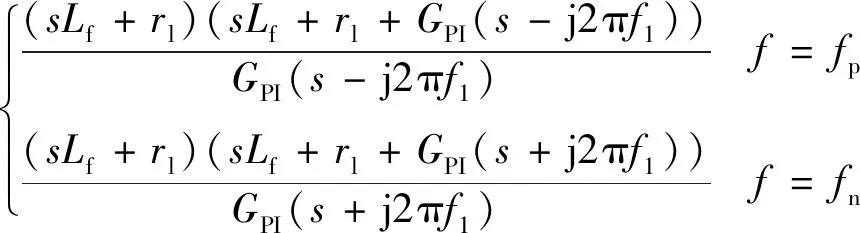
(31)

(32)

(33)

R(s)=(LfCfs2+rlCfs+rcCfs+1)/(rcCfs+1)

(34)

2.2 阻抗特性分析

依据表1参数数据绘制有、无电网电压前馈控制的输出阻抗模型对比图，如图5所示。

表1 VSG主要参数Table 1 Main parameters of the VSG

由图5可知，在低频段2种控制策略下的阻抗模型曲线完全重合，而在高频段带前馈控制的阻抗模型由容性提升为感性。针对各控制环节与阻抗模型的关系有如下分析。

图5 2种控制下的VSG输出阻抗模型Fig.5 VSG output impedance models of two controls

(1)功率外环与阻抗模型的关系。VSG低频段阻抗特性与电流内环和电网电压前馈控制无关，仅表现为功率外环特性，受功率外环控制参数影响。

(2)电流内环与阻抗模型的关系。当扰动频率fp很高时，s趋于无穷，表达式T(s)，N(s)，M(s)以及PI调节器中的积分项ki/s趋于零，式(26)和式(27)的正负序阻抗模型可简化为式(35)。可知，高频段阻抗曲线主要受滤波电感Lf以及电流环比例调节系数kp影响。

(35)

图6和图7表现了带前馈控制阻抗特性曲线与电流内环PI控制器的比例系数kp、积分系数ki之间的关系。结合两图与式(35)可知，当kp减小到一定程度，或者ki增大至一定程度时，相位可能过大，造成谐波振荡；kp对10 kHz以上的频段阻抗幅值有影响，相位无影响，且相位最终都趋近于180°。

图6 kp与带前馈控制VSG输出阻抗的关系Fig.6 Relationship between kp and output impe-dance of VSG with feedforward control

图7 ki与带前馈控制VSG输出阻抗的关系Fig.7 Relationship between ki and output impe- dance of VSG with feedforward control

(3)前馈环节与阻抗模型的关系。根据图3中电网电压前馈控制，可以得到VSG的等效控制框图，如图8所示。前馈控制传递函数可等效为虚拟导纳，与电流环输出阻抗并联，从而对VSG输出阻抗产生影响。

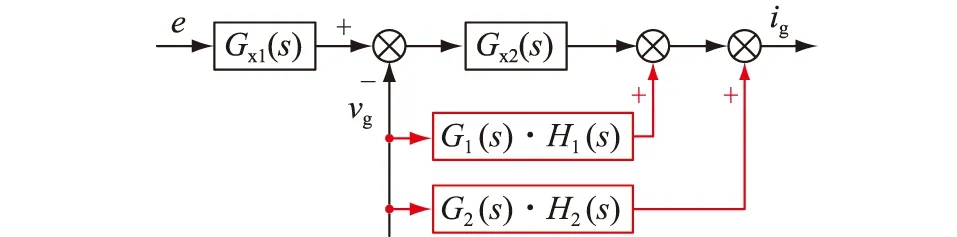
图8 前馈控制下的VSG等效控制框图Fig.8 Equivalent control block diagram of VSG with feedforward control

图8中各等效传递函数分别为：

(36)

(37)

(38)

(39)

(40)

为了分析前馈函数对阻抗的作用，结合式(7)可得前馈传递函数的伯德图，如图9所示。由图可知，G1(s)对小信号始终衰减，而G2(s)对VSG的阻抗特性高频小信号有放大作用，可改善调制波波形。同时，G2(s)导致相位超前，改变VSG阻抗高频段呈容性的特点，使相位大于0°，提高其与电网阻抗幅频曲线交截点处的相角裕度，改善并网稳定性。

图9 电网电压前馈函数伯德图Fig.9 Bode diagram of grid voltage feedforward function

3 并网稳定性分析

当VSG并网时，由阻抗分析法[23]可知，系统的稳定性可通过判断电网阻抗与VSG输出阻抗比值Zg(s)/Zo(s)是否满足奈奎斯特稳定判据进行证明。当Zg(s)与Zo(s)的幅频曲线相交频率点处的相角裕度γ=180°-|∠Zg(s)-∠Zo(s)|>0°时，系统稳定。在工程应用中，为增加交互系统的鲁棒性，通常要求γ>30°。

3.1 无前馈控制时的VSG并网稳定性

无前馈控制时的VSG正负序阻抗与电网阻抗曲线如图10所示，电网阻抗值Lg分别取为3 mH，8 mH和14 mH。

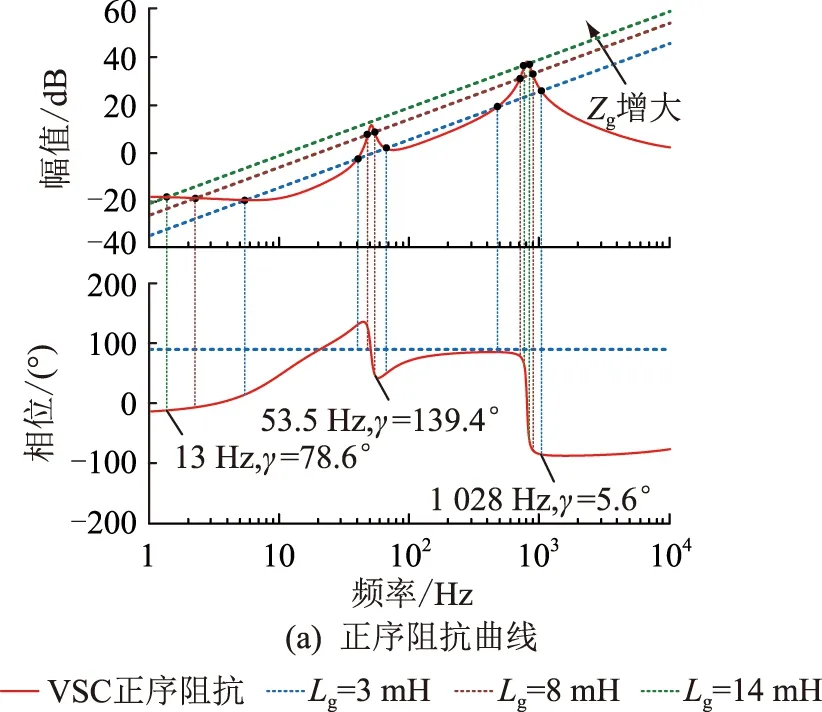
图10 无前馈控制下的VSG与电网阻抗特性曲线Fig.10 Sequence impedance curves of VSG without feedforward control and grid

通过分析阻抗幅频曲线交截点处的相位裕度可以发现，当电网阻抗Lg=3 mH时，受LC滤波谐振的影响，VSG高频段正负序阻抗均呈容性，电网阻抗与正负序阻抗在1 028 Hz产生交截，交互系统的相位裕度γ=5.6°，不满足实际工程的稳定性要求，若电网在该频次含有很小的背景谐波则极易引起整个系统的振荡。而当电网阻抗Lg=14 mH时，高频段交截点的相位裕度满足γ>30°，系统能够稳定运行。由此可知，当电网阻抗Lg较小时，其与VSG阻抗模型在高频段幅频曲线交截点处的相角裕度不满足工程稳定性要求。在实际应用中，通常通过适当增加阻尼电阻rc以改善并网系统的高频谐振，增加系统稳定性[24—26]。

3.2 带前馈控制时的VSG并网稳定性

带前馈控制时的VSG正负序阻抗与电网阻抗曲线如图11所示，通过分析图中正负序阻抗幅频曲线交截点处的相位裕度可以发现，交互系统均满足γ>30°，即无论电压阻抗如何变化，电网电压前馈控制下的VSG并网交互系统均能够稳定运行。

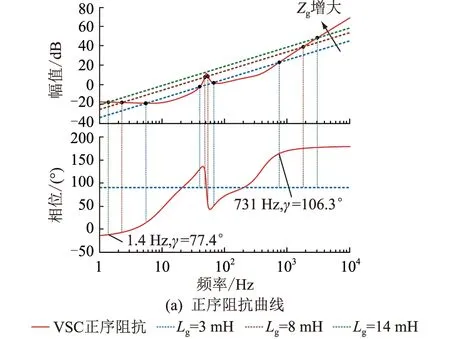
图11 带前馈控制下的VSG与电网阻抗特性曲线Fig.11 Sequence impedance curves of VSG with feedforward control and grid

4 实验验证及分析

为了验证前文理论分析的正确性，分别设计相应的仿真模型和实验平台，开展验证分析。

4.1 VSG输出阻抗模型验证

首先，为了验证理论阻抗模型的准确性，利用Matlab搭建带前馈控制的VSG仿真模型。在公共连接点注入不同频率的电压扰动信号，测量对应频率下的电流响应信号，求解该频率下的实测阻抗。VSG正、负序阻抗伯德图和仿真扫描结果如图12所示。

图12 带前馈控制下的VSG输出阻抗测量Fig.12 Sequence impedance measurement of VSG with feedforward control

由图12可以看出，理论阻抗曲线与测量结果非常吻合，验证了所建立模型的准确性。

4.2 VSG并网稳定性实验验证

基于实时仿真实验平台(real-time laboratory,RT-LAB)建立VSG并网的硬件在环实验平台。图13为RT-LAB平台系统结构。外部数字信号处理器(digital signal processor,DSP)控制器实现VSG的控制电路，RT-LAB平台仿真模拟VSG接入不同电网的系统主功率电路，并通过平台自带的数/模转换接口实现输出采样和输入控制。

图13 RT-LAB平台系统结构Fig.13 System structure of RT-LAB platform

为验证电网电压前馈控制对背景谐波的抑制效果，在电网中人为注入5次、7次以及11次谐波来模拟电网电压的背景谐波。图14给出加入电网电压前馈控制前后的并网电流对比波形。

图14 电网含谐波条件下实验波形Fig.14 Experimental waveforms when grid has harmonics

由图14可以看出，采用电网电压前馈控制后，VSG的输出电流波形比无前馈控制时谐波含量显著减少。实验结果说明了电网电压前馈控制可以消除电网电压背景谐波对并网电流的影响，改善波形质量。同时，也验证了前文前馈控制环节设计与分析的正确性。

为验证电网电压前馈控制对并网稳定性的影响，取电网阻抗Lg为3 mH，且含少量背景谐波。图15、图16给出加入电网电压前馈控制前后的并网电流波形及快速傅里叶变换(fast Fourier transformation，FFT)分析对比，M为其他频率电流与50 Hz频率电流的比值。

图15 无前馈控制下的VSG并网电压电流分析Fig.15 Grid-connected voltage and current analysis of VSG without feedforward control

图16 带前馈控制下的VSG并网电压电流分析Fig.16 Grid-connected voltage and current analysis of VSG with feedforward control

由图15、图16可以看出，无前馈控制时，受电网背景谐波的扰动，VSG的并网电流出现明显的振荡。FFT分析结果显示，并网电流在1 028 Hz频率处出现了大量的谐波，该频率与图10中的理论分析完全吻合。而采用前馈控制后，VSG并网电流波形及FFT分析显示并网电流谐波含量极小，验证了图11中理论分析的正确性。