基于压电材料的变压器振动能量收集装置研究

张琛，熊庆，汲胜昌，庄哲，张凡

(电力设备电气绝缘国家重点实验室(西安交通大学)，陕西 西安 710049)

0 引言

变压器作为电力系统核心设备，其安全稳定运行对电力系统的供电可靠性至关重要。在长期运行下，变压器绕组和铁芯不可避免地会由于老化而发生故障[1]，振动检测法是针对变压器绕组及铁芯状态的在线监测方法之一[2]。由于使用振动传感器需要有线电源、电池或挂线感应式能量收集装置进行供电[3]，限制了振动测量传感器的安装范围和使用寿命。在变压器的运行过程中，其本身存在振动。因此，收集变压器正常运行条件下的振动能量，为振动测量传感器供电，不但可以减小安装在线监测设备对变压器安全稳定运行的影响，还可以实现自取能以延长设备的单次使用寿命。

根据振动能量转换为电能的不同原理，振动能量收集装置主要分为电磁式[4]、静电式[5—6]和压电式[7—10]。压电式能量收集装置的基本原理是压电效应。压电陶瓷在某个方向上受到外部作用力而发生变形时，其内部会产生极化现象，并在其表面出现电荷量相等但正负相反的电荷；当作用力的方向发生变化时，电荷的极性也会发生变化；当外力撤出后，压电陶瓷又会恢复到原来不带电的状态，这种现象称为正压电效应。相比电磁式振动能量收集装置，压电式能量收集装置结构简单，不易受体积限制，且无需向电容施加初始电压作为静电式能量收集的初始条件，被广泛应用于电力设备振动状态监测[11]。文献[12]设计了一种压电式风能收集装置，装置由一侧开口的矩形谐振箱与压电梁构成，将压电元件的一端贴附于柔性梁上，另一端固定在谐振箱的顶部。气流流入谐振箱后带动柔性梁发生振动，实现将风能转化为振动的机械能，在柔性梁的振动下，压电元件发生形变并输出电能。在正向风速为17 m/s时，该装置能产生1.28 mW的输出功率，巧妙地利用风能带动悬臂振动实现能量的二次转换，但转换效率受风速与风向的影响较大。尽管目前国内外学者对振动能量收集方式与取能结构进行了大量的研究，但仍存在许多问题，例如：如何提高收能量收集效率[13]、扩大取能频率范围[14]、降低装置成本等。且由于压电材料刚度小，易疲劳，仍需大量理论和实验研究才能使其得到广泛应用。

文中设计针对变压器的压电式振动能量收集装置，建立仿真模型，获取能量收集装置的响应频率与发电能力，对其进行优化设计。搭建变压器振动能量收集实验平台，开展振动能量收集装置的测试实验，来验证装置的能量收集能力及可靠性。

1 压电式能量收集装置等效模型

压电式能量收集装置根据结构不同分为悬臂式、圆式与层堆叠式[15]。悬臂式结构主要应用于激励频率较低或振幅较小的振动激励，在质量块的作用下可以起到放大振动幅值的作用，使得压电元件产生较大形变。针对变压器外壳的振动特性，能量收集装置选择悬臂式结构。悬臂式压电能量收集装置主要由悬臂式压电元件、接口电路和负载三部分构成，如图1所示。压电元件实现振动能量向电能的转换，接口电路完成取能的电压整流，达到为后续负载供能的目的。

图1 悬臂式压电能量收集装置结构Fig.1 Structure of cantilever piezoelectric energy harvesting device

为研究压电振动能量收集装置负载端的端口电压，建立如图2所示的收集装置模型。其中，M，K，D分别为机械部分等效质量、刚度和阻尼；αε，Cp分别为能量采集装置压电片的机电转换系数与内部电容；F为施加在能量收集装置上的激励振动力；u为能量采集装置末端的振动位移；Vp，ip分别为压电元件的输出电压与输出电流，由此可建立压电式能量收集装置的运动控制方程。

图2 能量收集装置的等效机电模型Fig.2 Equivalent electromechanical model of energy harvesting device

根据压电器件的特性，建立如图3(a)所示的等效电路模型。其中，电源Vin为压电元件的输出电压；电阻Rm表示机械阻尼系数；电感Lm表示机械质量参数；电容Cm表示机械强度参数。耦合系数为n的变压器将机械域与电气域相连接，将机械域部分等效到电气域中，从而使压电元件等效为一个简单的非耦合模型，如图3 (b)所示，包括正弦电流源Ip，内部电容Cp和内阻Rp[16]。

图3 压电式等效电路模型与简化模型Fig.3 Piezoelectric equivalent circuit model and simplified model

2 压电式能量收集装置设计仿真

依据理论推导结果设计模型结构，先设计单悬臂梁式取能结构，研究不同参数对取能结果的影响，再利用变压器振动特性[17]，设计多模态[18]三悬臂式取能结构，拓宽取能频率，提高取能效率。

2.1 单悬臂式压电取能结构

在Comsol Multiphysics仿真软件中建立如图4所示的模型结构，基座部分选用不锈钢材料；悬臂部分选用厚度为0.3 mm的单晶片锆钛酸铅系压电陶瓷贴附在厚度为0.6 mm的不锈钢片两侧，形成3层的悬臂结构，悬臂臂长为170.3 mm，宽度为20 mm；重物选用不锈钢材料，大小为20 mm×20 mm×22 mm；基座部分固定在变压器外壳，即悬臂式压电结构的左侧作为固定面，基座部分随变压器振动一起产生振动，并带动悬臂振动，由于悬臂连接重物，在重物的影响下，悬臂两侧的压电片发生周期性形变，从而产生电能。

图4 单悬臂式压电取能结构Fig.4 Single cantilever piezoelectric energy extraction structure

在仿真中对压电能量收集装置整体施加周期性的载荷力，表示悬臂结构受变压器振动的结果。对施加载荷力的频率进行扫描，可以得到压电取能结构的固有频率，当外界激励频率接近悬臂结构固有振动频率时，压电能量收集装置达到最大取能峰值，结果如图5所示。

图5 单悬臂式压电取能结构外加激励频率与输出功率的关系Fig.5 The relationship between external excitation frequency and output power of one-cantilever piezoelectric energy extraction structure

由图5可以看出，当激励频率接近100 Hz时，压电能量收集装置的取能效果最佳。但同时，一旦激励频率偏离压电能量收集装置的固有振动频率，取能效果将大大减弱。

2.2 三悬臂式压电取能结构

针对变压器的振动特性分析，变压器振动主要由铁芯的磁致伸缩和绕组在负载电流作用下的安培力共同引起。铁芯的振动信号在频域谱图上表现为以100 Hz为基本频率，同时包含较多200 Hz，300 Hz，400 Hz等谐波。绕组的振动频谱图中包含丰富的倍频和高频谐波。据此可以设计多模态压电式能量收集装置，根据变压器的振动特性来拓宽取能频率，提高取能效率，设计结构如图6所示。

图6 三悬臂式压电取能结构Fig.6 Three-cantilever piezoelectric energy extraction structure

三悬臂式压电取能结构由三部分构成：支座部分、悬臂部分、重物部分。支座部分采用不锈钢材料，重物采用铅材料，悬臂部分则采用单层厚度为0.3 mm的压电陶瓷贴附于厚度为0.83 mm的不锈钢基片上。整体结构体积相比单臂式大幅减小，大小仅为30 mm×55 mm×15 mm。三悬臂臂长分别为35.3 mm，21.8 mm，16.3 mm，3个悬臂的固有振动频率分别为100 Hz，200 Hz，300 Hz。在100 Hz的外加激励下输出功率大约为0.03 W。

对三悬臂式压电取能结构进行仿真分析，结果如图7所示。由仿真结果分析可知，三悬臂式压电取能结构的固有振动频率分别为100 Hz，200 Hz，300 Hz。这3个频率作为取能结构的模态频率，当外界激励频率接近某个模态频率时，取能结构开始进行取能；而当外界激励频率是包含很多频率的复杂信号或具有一段频宽的频率信号时，压电取能结构可以有效提取模态频率下的振动能量，将其转换为电能。由于变压器振动是以100 Hz为基频，并含有200 Hz，300 Hz等谐波频率，因此设计该结构可以提高整个压电式能量收集装置的回收效率。

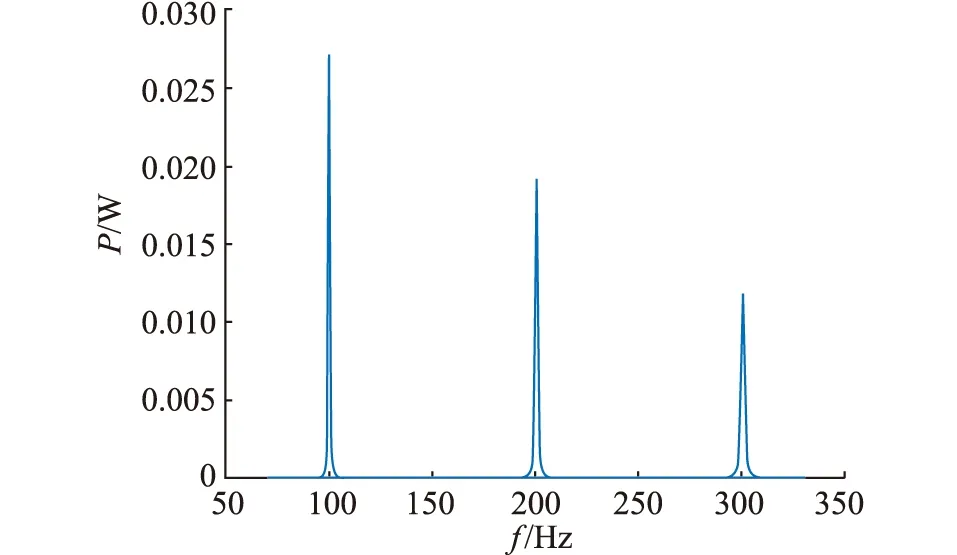
图7 三悬臂式压电取能结构外加激励频率与输出功率的关系Fig.7 The relationship between external excitation frequency and output power of three-cantilever piezoelectric energy extraction structure

三悬臂式取能结构在固有振动频率下输出功率分别为0.027 3 W，0.018 4 W，0.012 1 W。后续能量回收电路需要对3个悬臂的取能结果分别进行处理，经过整流电路后作为3个并联的稳定直流源，实现振动能量向电能的转换。

3 实验搭建与结果分析

3.1 振动能量及测量平台搭建

选用原边电压400 V，副边电压10 kV，额定容量为50 kV·A的电力变压器，变压器示意如图8所示。

图8 变压器外壳网格划分Fig.8 Grid graph of the transformer shell

变压器外壳宽180 cm，深100 cm，高85 cm，从左到右依次为A、B、C三相绕组。对变压器外壳进行等距地网格划分并对网格点进行编号，由于实际的能量收集装置不便安装于变压器表面边缘，故忽略边缘处标号。将3×6点列所在面称为正面，3×3点列所在面称为侧面，测量在变压器负载运行下不同网格点的振动情况。

外壳温度为18 ℃，由于在实验过程中，油箱上部和下部的温差约为8 ℃，因此记录油箱中部温度作为变压器外壳温度。在网格点位置安装测量振动加速度的传感器，测量负载运行条件下各点的振动加速度。经测量得到测点7处振动最为明显，即变压器A相绕组中间位置。测点7的频谱分析如图9所示。该点的振动频率以100 Hz为主，振动加速度为2.19 m/s2，含有较少的50 Hz和200 Hz的谐波分量。

图9 测点7频谱分析Fig.9 Spectrum analysis of measuring point 7

3.2 压电式振动取能结果检测与验证

将三悬臂式压电取能结构通过热熔胶固定在变压器外壳上，测量实际取能效率。实验平台与实物如图10所示。

图10 压电式能量收集装置Fig.10 Piezoelectric energy harvesting device

压电式取能结构贴附在变压器外壳振动加速度最大位置处，此处振动加速度为0.22g(g为重力加速度)，小于仿真中施加给悬臂结构1g的外加振动激励。因此实际共振条件下压电式能量收集装置的输出功率P′1与仿真得到的理论输出功率P0的关系为：

(1)

为了验证压电式取能结构的实际输入功率，将压电式能量收集装置与标准的取能电路相连接，中间接入阻值为100 kΩ的测量电阻Rc，通过测量电阻Rc两端的电压差，计算输入电流，进而得到输入功率，同时每隔30 s测量储能电容两端的电压，得到电容所储能量，并计算电路效率，测量的结果如图11所示。其中，U1为输入电压，U2为测量电阻之后的电压。

图11 输入电压与测量电阻之后电压Fig.11 Input voltage and voltage after measuring resistance

根据实验数据与瞬时输入功率，经过计算后可得实际平均输入功率P1为11.547 μW。

(2)

将实际的压电式能量收集装置的输入功率P1与仿真得到的理论输出功率P0比较：

(3)

研究发现实际输出功率远小于理论仿真中达到共振条件下的输出功率。分析原因可能为压电式能量收集装置的固有频率与变压器振动频率存在一定偏差，没有达到共振条件。输出功率为共振条件下输出功率的1/134。将实际测量的输入功率代入仿真中如图12所示的输出功率与激励频率的关系，可以推断出压电式能量收集装置的固有频率较变压器外壳振动频率100 Hz相比偏差约为3 Hz。

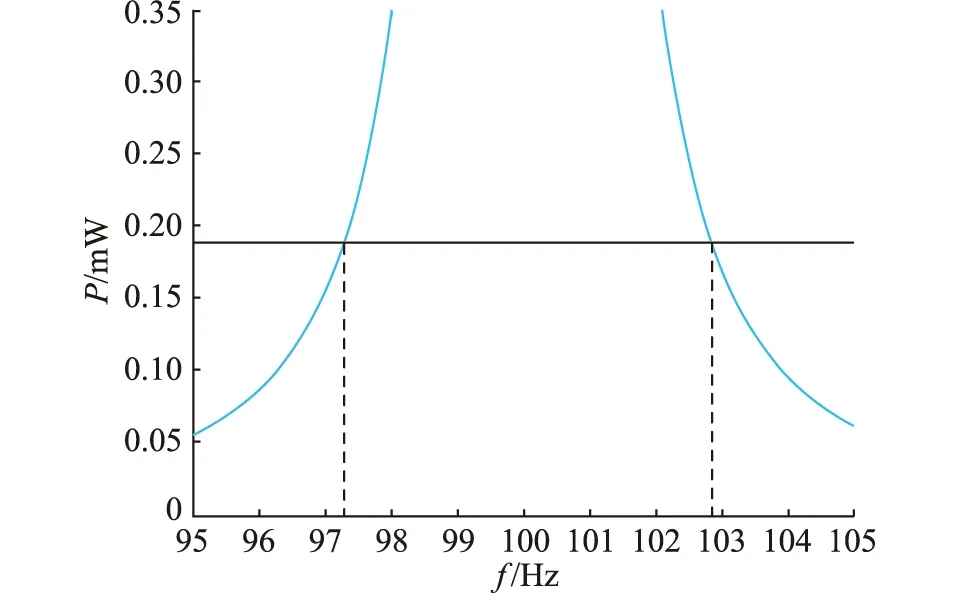
图12 输出功率与激励频率的关系Fig.12 The relationship between output power and excitation frequency

由于压电式取能结构较小，改变铅块质量引起的固有振动频率变化幅度较大。因此，该结构仍有优化空间，拓宽能量收集装置的谐振频率对于提高能量回收效率具有极为重要的意义。

4 结语

文中研究了振动能量收集装置的结构与能量收集转换电路的性能等，利用多模态的方法，设计了可贴附于变压器外壳的三悬臂式压电取能结构，并对能量收集装置进行了模拟仿真与实验研究。通过搭建变压器振动的能量收集实验平台，测得变压器外壳最大振动加速度为2.19 m/s2，并在变压器外壳振动最明显处安装能量收集装置，测量得到输出功率最高可达11.55 μW。根据外加激励频率与输出功率之间的关系，可推断出压电式能量收集装置的固有振动频率较变压器外壳激励频率偏差在3 Hz内。装置本身结构仍值得进一步完善与优化。为保证振动能量收集装置不影响变压器的正常运行，取能结构仍可在微型且高效的方向上继续优化。