基于V-I轨迹与高次谐波特征的非侵入式负荷识别方法

2021-12-01裘星尹仕红张之涵谢智伟江敏丰郑建勇

电力工程技术 2021年6期

裘星，尹仕红，张之涵，谢智伟，江敏丰，郑建勇

(1.深圳供电局有限公司，广东深圳 518048；2.东南大学电气工程学院，江苏南京 210096)

0 引言

随着国民经济的迅速发展，人民的生活水平获得了显著的提高，居民对家用电器的使用也大幅增加[1—3]。然而由于一部分家用电器，特别是含有大量高次谐波电流的家用电器，如电吹风、洗衣机等，存在着一定的安全隐患，因此需要对家用电器使用情况进行识别，进而排查潜在安全风险。非侵入式负荷识别技术可以实时监控用户侧用电设备的类型、运行状态和功率大小等，识别用户用电安全隐患，帮助用户排查安全风险，从而指导居民的安全用电[4—5]。

在非侵入式负荷识别技术的研究上，国内外学者做了大量的工作。文献[6]根据不同负荷的稳态电流特征，构建自回归移动平均模型(autoregressive moving average model，ARMAX)线性负荷与哈默斯坦(Hammerstein)非线性负荷的模型数据库，对未知负荷进行模型匹配以实现负荷类型识别，然而提出的多项式模型难以准确反映负荷的电流谐波特征。文献[7]选取负荷的有功功率和电流3次谐波幅值作为特征，利用遗传优化实现负荷识别，然而忽略了家用负荷的高次谐波特征。文献[8]选取电流前13次奇次谐波电流幅值作为负荷特征，并分别使用4种监督学习方法进行负荷识别，然而所提取的各次谐波幅值不能表现各次谐波在一个周期内的位置，无法完整描述波形特征。文献[9]绘制了不同负荷的V-I轨迹图像，通过对比分析证明了不同工作原理的设备(如电阻型、电机驱动型或电力电子型)拥有其独特的V-I轨迹图像，辨识度较高。然而V-I轨迹图像只能描述归一化后的电压、电流之间的关系，难以反映负荷实际功率的大小关系，即不能区分大功率负荷与小功率负荷。因此文献[10]提出了一种基于V-I轨迹特征与功率特征相结合的负荷辨识算法，证明了复合特征相比于简单的V-I轨迹图像特征有着更高的负荷辨识度，可以准确区分拥有相似的V-I轨迹但功率差距较大的家用电器。然而，为保证卷积神经网络(convolutional neural network,CNN)有较快的训练速度，将对V-I轨迹图像进行高度像素化，导致其难以反映负荷电流的高次谐波特征。且所提方法使用了3种不同的神经网络模型进行特征提取与辨识，需要耗费大量的时间进行参数调节，导致此方法的运用受到了一定的限制。上述方法均不能准确提取家用电器的高次谐波特征，难以检测用户用电的安全隐患。

针对上述问题，文中对传统的V-I轨迹矩阵特征进行改进，融合了高次谐波电流特征及功率特征，组成混合特征矩阵，弥补了家用电器V-I轨迹矩阵高度像素化带来的特征损失，再利用CNN进行特征辨识。对插头级电器识别数据集(plug-level appliance identification dataset,PLAID)，家用电器数据集和深圳某小区用户家用电器实测数据进行算例分析。实验结果表明，混合特征矩阵能够克服V-I轨迹矩阵高度像素化带来的特征损失，可以正确区分V-I轨迹矩阵相同、功率大小也相近的家用电器，极大地提高了对加热器和吹风机的辨识正确率，且所提方法的负荷辨识正确率相对于传统的V-I轨迹图像特征辨识法有明显提升。

1 家庭负荷的V-I轨迹图像对比

家庭负荷的供电电压一般来说是比较稳定的，不同负荷的电压波形基本一致，而反映负荷典型特征的主要是电流波形[11—12]。常用的V-I轨迹图像的作用是以图形化方式反映电流波形特征，通过构建一个稳态周期内家用电器归一化后的电流与电压间的函数关系，并绘制图像进行描述。

图1为不同负荷在一个周期内的V-I轨迹图像，表1为不同负荷的有功、无功功率特征。通过比较可得，大部分家用电器的V-I轨迹图像和有功、无功功率差异较大，然而加热器与吹风机这2种负荷的电流波形和V-I轨迹图像的相似度较高，且两者的有功功率与无功功率差距极小。由于吹风机含有大量高次谐波电流，在使用中存在一定的安全隐患，而加热器相较而言更为安全，因此，实现2种家用电器的准确辨识有助于排查使用含有大量高次谐波的家用电器的潜在安全风险，也是一个研究难点[13—15]。

图1 各类家用电器的V-I轨迹图像Fig.1 V-I track images of various family loads

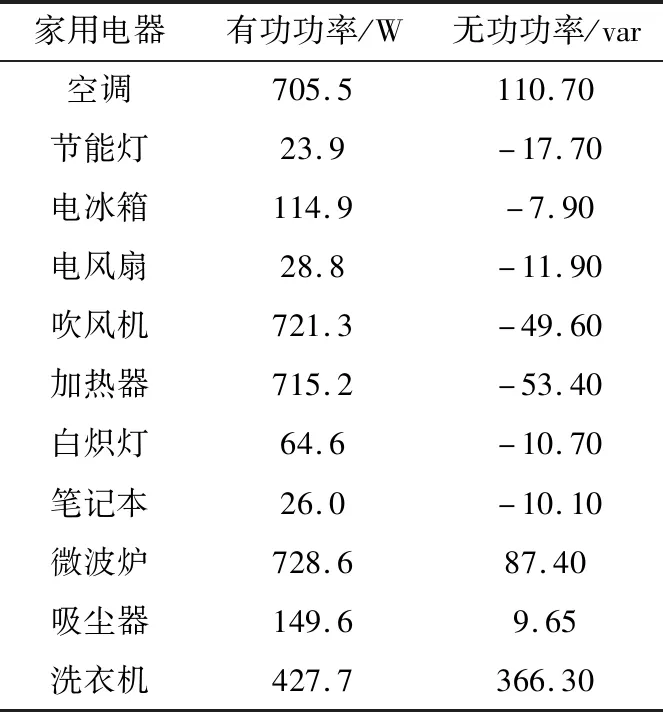
表1 各类家用电器的有功与无功功率Table 1 Active and reactive power of various family loads

为降低特征的复杂度，在特征提取的过程中需要将V-I轨迹图像高度像素化。图2为吹风机与加热器的22阶V-I轨迹矩阵图像，可见像素化后2种用电器的V-I轨迹图像几乎完全一致，给两者的正确分类带来了极大的难度。

图2 2种家用电器的V-I轨迹矩阵Fig.2 V-I trajectory matrix of two family loads

文中从频域分量方面对2种家用电器进行了深入研究，利用快速傅里叶变换(fast Fourier transform，FFT)对两者电流信号的基波及各次谐波的幅值进行了比较，如图3所示。

图3 2种家用电器的电流谐波幅值对比Fig.3 Amplitude histogram of harmonics of current of two family loads

由图3可见，吹风机与加热器在谐波分布上最明显的差异是，加热器只含有极少的9次谐波分量，而吹风机则包含较多的9次谐波，这些9次谐波分量主要是由吹风机内部无刷直流电机产生[16]，而加热器内部没有直流电机，因此高次谐波分量也较少。

选择高次谐波的含量作为附加特征，与像素化的V-I轨迹图像以及家用电器有功、无功功率组合为混合特征，从而弥补V-I轨迹图像高度像素化所带来的高次谐波特征损失问题，提高负荷识别的正确率。

2 基于V-I轨迹矩阵与高次谐波的特征融合算法

2.1 V-I轨迹矩阵提取方法

由于V-I轨迹表征负荷电压波形与电流波形之间的关系，不同负荷的V-I轨迹差异在于轨迹的形状，因此难以使用常见的信号处理方法，如FFT、小波变换等算法进行特征提取。因此，文中使用二维图像矩阵描述不同类型家庭负荷的V-I轨迹特征，具有计算简单且还原效果较好的优点[17]。计算步骤如下：

(1)提取负荷在一个周期内的电压电流波形，并将2种波形数据归一化至[0,1]范围内。

(2)构建N×N阶二维矩阵M作为V-I轨迹矩阵，矩阵在初始状态下的所有元素均为0。

(3)利用下式将电压电流波形映射至N×N阶二维矩阵中。

a=⎣V(p)×(N-1)+1」

(1)

b=⎣I(p)×(N-1)+1」

(2)

M(a,b)=1

(3)

式中：V(p)，I(p)分别为归一化后第p个采样点的电压与电流值；a，b分别为矩阵M的行索引和列索引；⎣」为向下取整符号。通过式(1)—式(3)可绘制V-I轨迹矩阵，如图4所示，N取20，白色表示矩阵元素为0，黑色表示矩阵元素为1。

图4 V-I轨迹矩阵Fig.4 V-I trajectory matrix

2.2 补充特征的提取方法

为了防止特征数据过于庞大，延长有监督学习的训练时间，在使用V-I轨迹矩阵描述负荷的电流波形特征时会适当减少矩阵阶数，进而降低了对电流波形的采样精度，这导致了一部分高次谐波特征，如9次谐波特征难以体现在V-I轨迹矩阵中，会对家用电器辨识造成一定的偏差。因此，文中选取了电流高次谐波以及有功、无功功率作为补充特征，高次谐波特征可以弥补V-I轨迹矩阵采样精度不足的缺点，而有功、无功功率特征可以区分大功率用电器与小功率用电器，两者可以极大提高负荷辨识的正确率。

运用FFT对一个周期内的负荷电流波形进行处理，将时域信号转化为频域信号，如式(4)所示。

(4)

式中：k为谐波次数；X(k)为第k次谐波的频域分量，使用复数表示；i(n)为第n个电流采样点；L为一个周期内的电流采样点个数。X(k)的模值表示了第k次谐波的幅值，而X(k)的幅角表示了第k次谐波的相位[18—19]。

由图3可以看出，家用电器的稳态电流波形中，奇次谐波的幅值远大于偶次谐波，且当谐波次数大于11次时幅值已经非常小，容易混入大量干扰噪声，因此文中选取7，9，11次谐波作为高次谐波特征。

高次谐波的幅值计算如式(5)所示。

Ai(k)=|Xi(k)|

(5)

式中：Ai(k)为电流第k次谐波的幅值；Xi(k)为电流第k次谐波的频域分量；k分别取7,9,11。

谐波特征除了包含幅值外，相位也是极为重要的参数。图5展示了加热器与吹风机这2种家用电器的奇次谐波相位。由图5可得，2种家用电器的高次谐波相位值各不相同，其中加热器的9次谐波相位为负，而吹风机的9次谐波相位则为正，因此电流高次谐波的相位特征也可以辅助区分不同家用电器。

图5 2种家用电器的电流奇次谐波相位直方图Fig.5 Phase histogram of odd-order harmonics of current of two family electrical appliances

为保证相位特征的准确性，选取电流各次谐波相位与电压各次谐波相位的差值作为相位数据进行特征辨识，如式(6)所示。

φ(k)=argXi(k)-argXu(k)

(6)

式中：k分别取7,9,11；Xu(k)为电压第k次谐波的频域分量；φ(k)为最后提取出的各次谐波相位值；arg为幅角运算函数。

2.3 混合特征矩阵的构建

将功率特征、高次谐波特征和V-I轨迹矩阵进行整合，形成混合特征矩阵，方便识别算法的后续运算。使用二进制编码的方法对功率与高次谐波特征进行处理，再添加至V-I轨迹矩阵中形成混合特征矩阵，具体步骤如下。

(1)确认特征顺序，共8个补充特征，从左至右分别为：7次谐波幅值，9次谐波幅值，11次谐波幅值，7次谐波相位值，9次谐波相位值，11次谐波相位值，有功功率值和无功功率值。

(2)根据式(7)将不同样本的同一特征归一化至[0,2N-1]范围内。

Sm,g=⎣(sm,g-smmin)/(smmax-smmin)×(2N-1)」

(7)

式中：g为样本编号；m为特征编号，取1,2,…,8；Sm,g为归一化后第g个样本第m个特征值；sm,g为归一化之前第g个样本第m个特征值；smmin，smmax分别为第m个特征下最小和最大的样本特征值。

(3)将上述归一化后的特征值转换为N位二进制数。比如N=8，归一化后的特征值为181，则二进制数为10110101。

(4)构建N×8阶二维特征矩阵F作为补充特征矩阵，矩阵在初始状态下的所有元素均为0。

(5)使用式(8)将二进制数的各位填入矩阵F中。

Fg(a,m)=binm,g(a)

(8)

式中：a为二进制位索引，范围为[1,N]；Fg(a,m)为第g个样本的补充特征矩阵F的第a行第m列元素值；bin为二进制运行函数，即binm,g(a)为第g个样本第m个特征下的二进制特征值的第a位。

(6)将F矩阵添加到V-I轨迹矩阵右侧，即M矩阵的第N+m列为F矩阵的第m列，形成一个N×(N+8)阶的混合特征矩阵W，如图6所示。

图6 混合特征矩阵Fig.6 Fusion feature matrix

图7展示了文中负荷辨识的流程，主要包含家用电器稳态数据采集、特征提取、特征组合与负荷识别4个步骤。

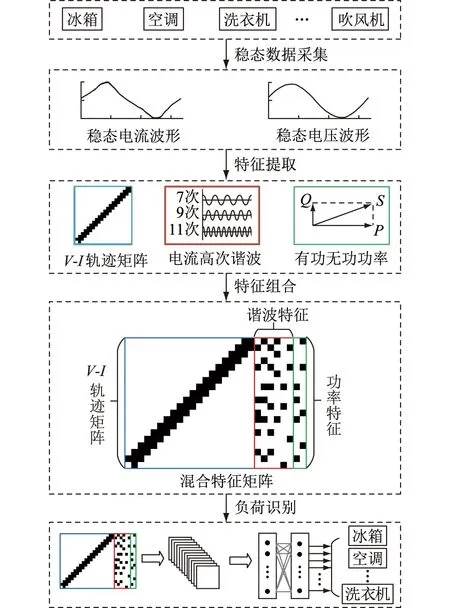
图7 负荷辨识流程Fig.7 Flow of load identification

3 CNN的构建方法

第2章为每一个样本建立了N×(N+8)阶的混合特征矩阵W，由于矩阵元素的取值只有0和1，因此可以将矩阵视为黑白图像，进而使用图像识别技术进行特征提取。文中选用CNN进行矩阵特征的识别，相比于其他全连接神经网络，CNN在训练二维图像数据的过程中可以保留数据的空间特征，拥有较高的训练效率，且不容易出现网络过拟合的情况。其结构如图8所示，其中N取20。

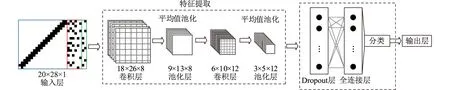
图8 CNN的结构示意Fig.8 Schematic diagram of the structure of the CNN

由图8可得，CNN的输入层维度与混合特征矩阵维度相同，输出层的维度与待分类负荷种类数量有关，而CNN的隐含层是由卷积层、池化层、Dropout层和全连接层组成的，其中卷积层和池化层交替重复，且上一层的输出直接作为下一层的输入[20—21]。

卷积层的作用是进行输入数据特征提取，由多个卷积核组成。卷积核也被称为滤波器，其内部权重均由多次反向传播修正而来。使用卷积核对输入特征进行从左到右、从上到下的扫描，对扫描区域进行卷积运算，可以提取输入图像的特征。

池化层的作用是对输入图像进行压缩，从而降低下一层的输入维度，提高运算效率。同时池化层也能减少网络参数的数量，达到抑制过拟合的效果。文中选取的池化层过滤器大小为2×2，因而可以将输入单元数缩小4倍输出，极大地加快了训练过程[20]。

Dropout层工作的原理是：层内的神经元在前向传导的过程中，每一个神经元都有一定概率停止工作，即无法向后续神经元传递信息。通过设置Dropout层，可以提高网络的训练速度，防止过拟合现象的出现，提高模型的鲁棒性。

最后一层全连接层的激活函数为Softmax函数，损失函数为交叉熵损失函数，其作用是实现样本的分类，输出向量的维度与样本总类别数相同，向量的第i个元素代表了本次辨识结果为第i类设备的概率，所有元素的和为1。文中选取的损失函数为平方损失函数，在每一次训练结束之后，全连接层都会将分类结果与样本实际类别进行比对，利用损失函数计算训练误差，再微调网络中神经元之间的权重，进行下一次训练。对网络进行多次训练的目的是使损失函数最小化，保证样本实际类别对应的元素概率值最大，从而达到最佳的分类效果。

深度学习算法CNN的本质是使用大量的特征滤波器进行特征提取，并进行层层卷积与池化，进而一步步地从混合特征矩阵中提取有效特征，构建分类规则。一般来说，网络层数越多，则提取的特征也越具有代表性。文中建立的CNN结构如表2所示。

表2 CNN的具体结构Table 2 Specific structures of CNN

4 算例分析

4.1 PLAID数据集算例分析

文中选用PLAID数据集对所提出的负荷识别算法进行验证。PLAID数据集包含了11类家用电器，总共有1 793组样本数据，以采样频率30 kHz记录了每一个样本单独运行超过2 s的电压与电流信号[22]。由于大部分家用电器的开启瞬态过程都能控制在2 s以内，因此从数据集的每组数据中均能提取家用电器稳态运行波形[23]。然而，在PLAID中，不同类别的家用电器样本数量有较大差距，样本数量最多的几类家用电器，如吹风机、微波炉、空调和笔记本电脑等，均包含超过200个样本，而如冰箱、洗衣机、吸尘器和加热器等家用电器，均只包含70～80个样本，样本数量的不平衡度较高。因此文中选用了合成少数类过采样技术(synthetic minority oversampling，SMOTE)对少数类样本进行过采样，保证不同类别家用电器的样本数量大致相同[24]。过采样算法的具体步骤如下：

(1)对少数类中的每一个样本x，计算其与其他所有样本之间的欧氏距离，形成x对应的K近邻。

(2)设置过采样倍率R，即运算结束后少数类的样本个数增加至R倍。对于每一个样本，从其K近邻中随机选择R个样本，分别为x1,x2,…,xR。

(3)利用式(9)生成新样本：

xi,new=x+Rrand(0,1)×(x-xi)

(9)

式中：xi,new为新生成的样本；xi为上述随机产生的样本；Rrand(0,1)为生成一个在0和1之间的随机数。

文中从扩充后的样本中，每一类家用电器选取75%作为训练集，选取剩余的25%作为测试集。表3展示了不同类别的家用电器训练集与测试集的样本数量分布情况。

为评估文中所提算法的准确性，利用混淆矩阵展示各类用电器的识别正确率[25]。算例使用的混淆矩阵为11×11阶方阵，混淆矩阵的行表示家用电器的真实类别，而混淆矩阵的列表示神经网络的预测类别，矩阵第i行第j列元素代表神经网络将真实类别为i的样本预测为j类的数量。混淆矩阵一般使用召回率R、精确度P、平衡分数Q和总识别率Ac来描述识别的总体效果，计算公式分别为：

(10)

表3 不同类别家用电器的训练集与测试集样本分布Table 3 Sample distribution of training set and testing set of different types of family electrical appliances

(11)

(12)

(13)

个数；Ri为第i类电器的召回率；Pj为第j类电器的精确度。当Ac和Q值越大时，表示分类器的判断效果越好。表4展示了使用混合特征进行负荷识别的混淆矩阵，图中类别序号1～11分别表示空调、节能灯、电冰箱、电风扇、吹风机、加热器、白炽灯、笔记本、微波炉、吸尘器和洗衣机，测试样本的平衡分数值分别为90.5%，98.1%，88.5%，94.0%，92.9%，97.0%，89.7%，89.7%，97.4%，97.3%，90.4%。

表4 测试样本混淆矩阵Table 4 Confusion matrix of test data

在特征提取的有效性方面，相比直接使用V-I轨迹矩阵进行负荷辨识和文献[10]所提融合V-I轨迹矩阵与功率特征的负荷辨识算法，文中所提算法拥有极大的优越性。表5对比了文中所提算法、基于V-I轨迹矩阵的负荷辨识算法以及文献[10]所提负荷辨识算法的正确率，3种算法的总正确率分别为93.2%，80.9%和89.0%。可以看出，混合特征可以极大地提高辨识正确率，特别是5号吹风机与6号加热器，这2种家用电器之间没有错误识别的现象发生。同时文中所提算法对其他类型家用电器均有较好的识别效果，总辨识正确率超过93%。

表5 3种方法辨识正确率对比Table 5 Comparison of the accuracy of three identification methods %

为验证文中所提算法的优越性，对比了该算法与其他典型负荷辨识算法的识别速度与正确率。实验均基于PLAID数据集，实验环境为win10系统下CPU为Intel i7 10700k，GPU 为 GeForce RTX 2060 Super，内存为32 GB 的计算机，所用语言为Python 3.8，深度学习框架为PyTorch 1.6。使用11类家用电器，共1 793组样本数据进行训练。其中文献[10]提取了V-I轨迹图像特征与功率数值特征，利用CNN与反向传播(back propagation,BP)神经网络进行负荷识别；文献[8]提取负荷电流的奇次谐波特征，分别利用多层感知器(multilayer perceptron，MLP)神经网络、K最近邻(K-nearest neighbors，KNN)算法、逻辑回归(logistic regressive，LR)和支持向量机(support vector machine,SVM)进行负荷辨识，具体结果如表6所示。由表6可得，文中所提算法的单样本识别时间为1.02 μs，识别正确率为93.2%，在6种负荷辨识算法中均为最优，且在训练时间上也有着良好的表现，证明了算法的优越性。

表6 与其他负荷辨识算法的辨识效果对比Table 6 Comparison of the performance with other load identification algorithms

4.2 我国实测数据算例分析

文中基于我国广东地区家用电器计量数据进行算例分析，样本数据均来源于深圳某仪表公司的智慧能源终端。数据集包含了6种家用电器，分别是定频空调、电冰箱、吹风机、加热器、微波炉和洗衣机，总共有600组样本数据。由于不同类别的家用电器的样本数量大致相当，因此无需使用合成少数类过采样技术解决样本不平衡问题。与4.1节相同，每一类家用电器选取75%作为训练集，选取剩余的25%作为测试集。分类结果如表7所示，其中总正确率为97.5%。