基于DDPG策略的四旋翼飞行器目标高度控制
2021-12-01刘安林时正华
刘安林,时正华
(河海大学 理学院,江苏 南京 211100)
0 引言
四旋翼飞行器作为一种复杂的无人技术设备,凭借其质量轻、体积小、成本低、灵活机动的特点,在农业植保[1]、工业监测[2]、航空运输[3]、军事领域[4]等方面发挥广泛效用.为保证飞行器能高效完成任务,控制策略的设计至关重要.因此,许多研究着眼于对无人飞行系统进行智能化技术训练.
四旋翼飞行器是一种高度非线性、互相强耦联的欠驱动系统[5].此外,加上实际飞行环境中的外部干扰,如何设计控制策略变得尤为复杂.为解决上述困难,当前的研究提出了众多控制策略.经典的比例-积分-微分(PID)控制器[6]是根据系统误差进行负反馈的过程,在稳定的环境中已成功运用于四旋翼飞行器定高悬停、姿态控制等任务.然而,PID算法忽略了系统中的非线性因素,具有超调量大、易受外部干扰等缺点,并且采用试错法人工整定PID系数难以满足控制性能的要求.为解决模型的非线性问题,增强抗干扰能力,涌现了众多非线性控制策略,例如滑模控制[7]、反步法[8]、自适应控制[9]等.有些研究将上述几种方法整合以提升控制策略的鲁棒性[10,11],但是这些方法各有优缺,并且模型的复杂性会加大控制策略的复杂度,不利于实施.
在过去几十年中,人工智能的蓬勃发展也扩展到控制领域,许多研究学者基于神经网络、深度强化学习算法设计控制策略.具有强化学习功能的控制策略最早可以追溯到2005年,Waslande等[12]采用标准策略迭代方法实现了四旋翼飞行器的精准跟踪.近年来,Koch等[13]开发了高保真的仿真平台用于测试飞行性能,同时使用深度确定性策略梯度(DDPG)、信赖域策略优化(TRPO)以及近端策略优化(PPO)算法进行内环姿态控制,取得了比PID算法更优的效果.Wang等[14]以及Hu等[15]分别使用DDPG、PPO算法对四旋翼飞行器进行速度控制,表明该算法在质量和臂长方面的泛化能力优于PID算法.然而,现有的强化学习控制策略大多集中在姿态和速度控制,位置控制相对较少.Tiwari等[16]利用增强随机搜索(ARS)算法实现了对四旋翼飞行器的目标位置控制.
基于上述文献的启发,本文使用DDPG算法对四旋翼飞行器进行目标高度及悬停控制.强化学习算法可以使智能体直接与环境进行交互,从神经网络中直接学习控制策略且无须对动力学模型进行假设和简化.同时,DDPG算法控制策略使模型具有泛化能力.基于上述原因,本文使用DDPG算法对四旋翼飞行器进行目标高度及悬停控制.为达到目标高度控制效果,本文基于reward shaping理论设计了新颖的体现越界惩罚的奖励函数.由于智能体难以探索到最终目标,稀疏奖励很难达到效果,本文设置多个奖励引导智能体逐步到达目标.该函数设计越界惩罚,若智能体越界,将给出-10的惩罚并终止回合,解决了智能体易陷于环境边界问题.仿真结果表明,本文的目标高度控制策略的响应速度比PID算法更快;在稳态误差性能指标方面优于增强随机搜索(ARS)方法;在质量、臂长方面具有泛化能力.本文的主要内容安排如下:第一节建立了四旋翼飞行器的动力学模型,第二节主要介绍了所提出的基于深度确定性策略梯度的四旋翼飞行器的目标高度控制,第三节介绍了仿真实验的过程以及结果讨论,验证了DDPG控制器的有效性.第四节为全文结论.
1 四旋翼的动力学模型
本节将给出四旋翼飞行器的动力学模型的创建过程.四旋翼飞行器的基本结构如图1所示.

图1 四旋翼飞行器及机体坐标系
为描述四旋翼飞行器的位置和姿态,建立了两个坐标系统:地球固连坐标系和机体坐标系.四旋翼动力学模型主要根据牛顿第二运动定律建立,有
(1)
1.1 旋转运动
对于四旋翼飞行器的旋转运动,依据动量矩方程建立模型.四旋翼飞行器由四个螺旋桨提供升力,升力方向始终与机体轴z轴的方向一致,四个旋翼分布在距质心L的位置上.作用在机体上的总升力f为:
(2)
式(2)中:Ti(i=1,2,3,4)为不同螺旋桨提供的升力;ωi(i=1,2,3,4)表示螺旋桨转速;cT为系数.
通过分析由扭矩驱动的旋转运动和由升力驱动的平移运动的动力学方程来建立模型.针对旋转运动建立姿态动力学模型,将欧拉旋转方程应用于机体坐标系,则施加到四旋翼飞行器上的合外力矩M可以表示为
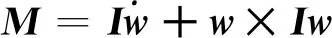
(3)
(4)
1.2 平移运动
对于平移运动,在地球固连坐标系中应用牛顿第二运动定律
(5)

(6)
式(6)中:S{·},C{·}分别表示sin(·),cos(·).最终,联立旋转运动和平移运动的动力学方程,可将四旋翼动力学表示为以下非线性微分方程:
2 深度确定性策略梯度(DDPG)算法
对于四旋翼位姿控制问题,主要目标是找到合适的控制策略以快速且稳定的方式将四旋翼从初始状态驱动到目标状态并悬停.基于策略梯度的算法最适合求解这类连续动作与连续状态的问题.通常使用基于期望回报的梯度来调整参数,寻找每一步的最佳动作,即策略梯度定理:
(7)
式(7)中:J(Aμ)为期望回报,ρAμ为策略Aμ的状态分布,QAμ(s,a)为实际状态价值函数.
深度确定性策略梯度(DDPG)算法是一种策略学习方法,在策略梯度算法中引入神经网络模型.本节将给出使用DDPG算法对四旋翼飞行器进行目标高度控制,并实现定点悬停的任务.确定性策略是一种将每个状态映射到最大概率的动作的策略,该动作是唯一确定的.因此,DDPG选择给动作空间添加扰动量以实现探索,本文使用的是OU噪声.
(8)
δt+1=rt+γQw(st+1,μ(st+1))-Qw(st,at)
(9)
式(9)中:rt为t时刻的奖励;γ为折扣率;Qw(st,at)为critic目标网络Q值.
critic网络通过最小化损失函数来更新参数:
Qw(si,ai))2
(10)
wt+1=wt+αwwL(w)
(11)
式(10)~(11)中:L为损失函数,N为批采样尺寸,w为critic网络参数,αw为critic网络学习率.
actor网络的目标是选出最佳动作,按DPG定理进行更新,更新方向为最大化Q值方向,actor网络更新方式如下:
(12)
μt+1=μt+αμμJ(μ)
(13)
式(12)~(13)中:J(μ)为期望回报;μ为actor网络参数;Aμ(s)为表征actor网络的策略;αμ为actor网络学习率.
四旋翼飞行器目标高度控制的确定性策略梯度算法的actor-critic网络结构如图2所示.
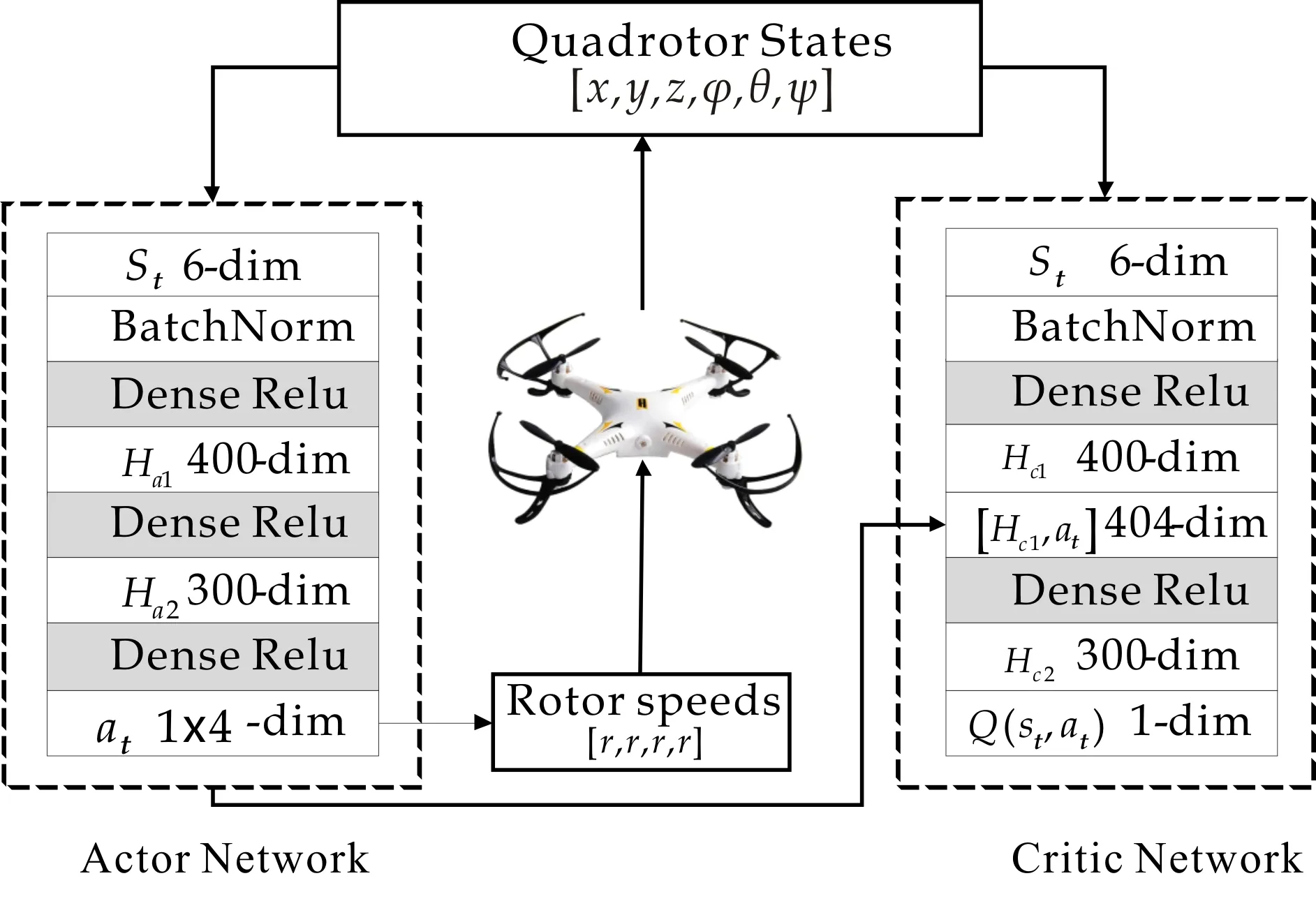
图2 四旋翼控制的DDPG算法的AC框架
此外,DDPG为增加学习过程的稳定性,分别创建目标actor网络、目标critic网络,在训练完经验回放的数据之后,通过梯度下降法更新当前网络参数,之后采用软更新方法更新目标网络参数.
w′←τw+(1-τ)w′
(14)
μ′←τμ+(1-τ)μ′
(15)
式(14)~(15)中:w′,μ′分别为目标critic网络参数及目标actor网络参数;τ为目标网络的学习率.使用DDPG对四旋翼进行目标高度控制的算法流程如下:

算法1 DDPG进行四旋翼目标高度控制随机初始化动作网络的权重Aμ随机初始化批评网络的权重Qw初始化经验回放池D加载简化的四旋翼动力学模型forepisode=1toMaxEpisodedo 初始化OU噪声以实现动作探索 观测初始四旋翼状态 fortimestep=1toMaxStepdo 选择动作at=Aμ(st)+nt 根据控制信号at来运行动力学模型 获得奖励rt并到达下一状态st+1 将经验(st,at,rt,st+1)存储到经验回放池中 从回放池中随机采样经验 根据公式(10)(11)更新批评网络 根据公式(12)(13)更新动作网络 根据公式(14)(15)更新目标网络 if超出安全范围then break endif endforendfor
3 实验与结果分析
3.1 实验说明
本实验使用深度确定性策略梯度算法对四旋翼飞行器进行位姿训练,使飞行器到达目标高度并悬停.使用第二节的动力学模型进行建模.基本的四旋翼参数如质量、尺寸、转动惯量展示如表1所示.
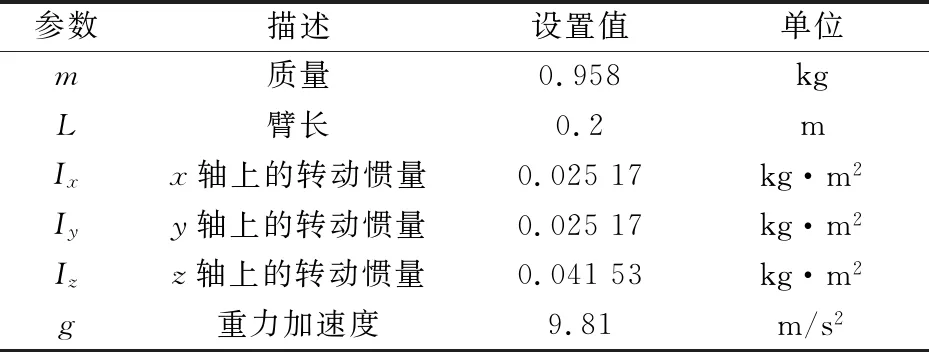
表1 四旋翼飞行器参数
本实验是在Windows操作系统上运行,处理器为Intel Core i7-9700CPU@3.00GHz.该无人机仿真使用Python进行编程.对于网络训练优化,本文使用的是内置Adam优化器.深度确定性策略梯度算法的网络训练参数设置如表2所示.
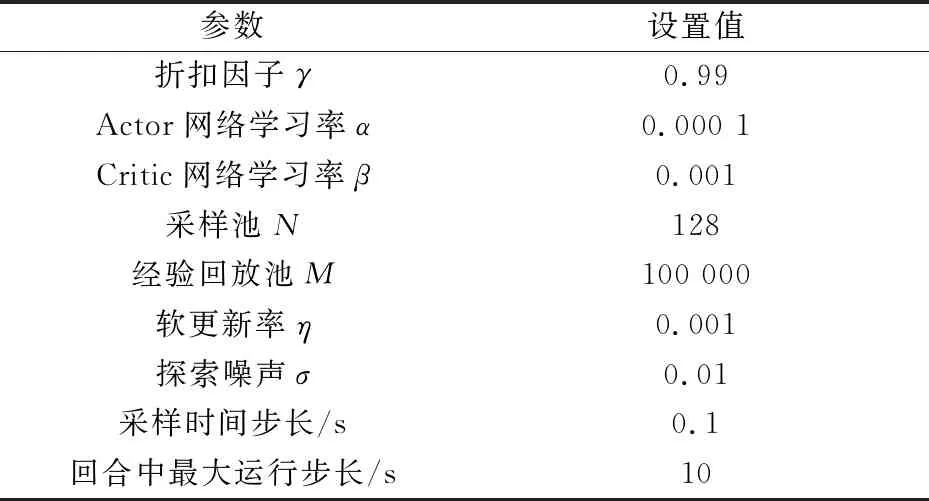
表2 DDPG算法训练参数
本实验的任务是利用深度确定性策略梯度算法将四旋翼飞行器从初始位置处垂直驱动至目标高度位置处悬停.首先初始位置是[0,0,0],设置目标高度为[0,0,10].本实验共进行1 200回合,每回合的最长运行时间为10秒,智能体每隔一个时间步长进行一次采样,时间间隔为0.1秒.
为保证四旋翼飞行过程中的安全,实验设置了安全范围,对于位置x,y,范围为[-150,150],对于高度z,范围为[0,300].出于安全考虑,实验的停止条件有两个,一是越过安全范围,二是超出回合最大运行时间.
3.2 目标高度控制任务
奖励函数作为强化学习中的核心部分,它引导智能体的期望行为,是强化学习的学习目标.针对四旋翼飞行器易陷入环境边界的问题,本文基于回报函数塑造(rewardshaping)理论,设计了一个新颖的体现越界惩罚的奖励函数,引导智能体在边界内运动.本文所设计的奖励函数为:
(16)
式(16)中:xe,ye,ze分别为当前坐标位置与目标坐标位置之间的差值,t为越界符号,未越界用0表示,越界用1表示.
本文基于reward shaping理论设计回报函数,由于智能体难以探索到最终目标,稀疏奖励很难达到效果.通过多个奖励设置引导智能体逐步到达目标.每个时间步长给基础奖励1,克服保守行为,鼓励智能体运动.以当前位置与目标位置之间的距离作为惩罚项.设计越界惩罚,如果智能体越界将给出-10的惩罚,并终止回合.
在奖励函数设计中,本文的一个新颖的体现越界惩罚的奖励函数,不体现越界惩罚的奖励函数为:
(17)
文献[17]中使用Soft Actor-Critic (SAC)算法进行四旋翼飞行器的位姿控制,将文献[17]中的奖励函数用于本文的DDPG框架中,所设计的奖励函数为:
(18)
本文将所设计的新颖的体现越界惩罚的奖励函数公式(16)与公式(17)以及公式(18)中的奖励函数进行试验对比,通过两个指标衡量任务的训练效果,一是累计奖励,二是稳态误差.本任务为目标高度控制,因此稳态误差计算的是每回合实际高度与目标高度之间的差值.在每回合中,较高的累计奖励意味着较低的稳态误差,越接近目标高度.训练过程中每回合的累计奖励以及稳态误差对比如图3~4所示.
从实验对比图可以看出,本文所设计的新颖的体现越界惩罚的奖励函数(公式(16))在训练后期收敛,且奖励值保持在一个很高的水平,而将文献[17]中的奖励函数用在DDPG算法中(公式(18))以及不体现越界惩罚的奖励函数(公式(17))进行实验,累计奖励一直在波动,并未收敛.从误差角度,本文所设计的奖励函数使得误差保持在一个较低的水平,训练后期逐步趋于0,而文献[17]中的奖励函数以及不体现越界惩罚的奖励函数误差还一直较高,说明本文所设计的新颖的奖励函数的有效性.
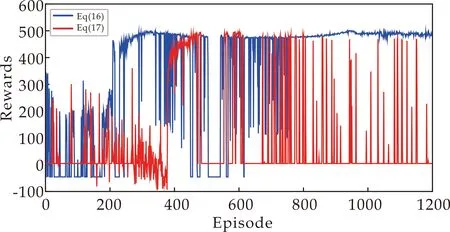
(a)累计奖励对比

(a)累计奖励对比
使用本文所设计的奖励函数的DDPG算法在训练的初期,没有收敛,因此奖励值很低并且波动较大,同时稳态误差很高.在750回合往后,奖励值逐渐升高,并且奖励值维持在一个较高的水平,说明训练效果较好且稳定.使用深度确定性策略梯度算法对四旋翼飞行器进行目标高度控制能够使稳态误差保持在一个很低的水平,进一步说明了该算法在四旋翼飞行器目标高度控制方面的有效性.为表明训练后期结果的稳定性,本文展示最后100回合的累计奖励和稳态误差的描述性统计,如表3所示.

表3 累计奖励、稳态误差描述性统计
在训练的最后100回合中,奖励值一直保持在一个很高的水平,且波动小,标准差为4.292 9,而稳态误差值同时保持很低的水平,标准差为0.943 5,说明训练效果稳定.
为测试算法的稳定性,使用DDPG算法进行目标高度的控制任务,将四旋翼由初始位置[0,0,0]驱动到[0,0,10]处悬停,并与整定良好的PID控制器进行对比,PID控制器参数设置为比例系数为15,积分系数为1,微分系数为15.结果如图5所示.从图5可以看出,在相同控制任务下,DDPG策略能够更快的到达目标高度,并在目标高度10 m处悬停,稍有抖动,而PID需要5秒左右才能到达目标高度悬停.
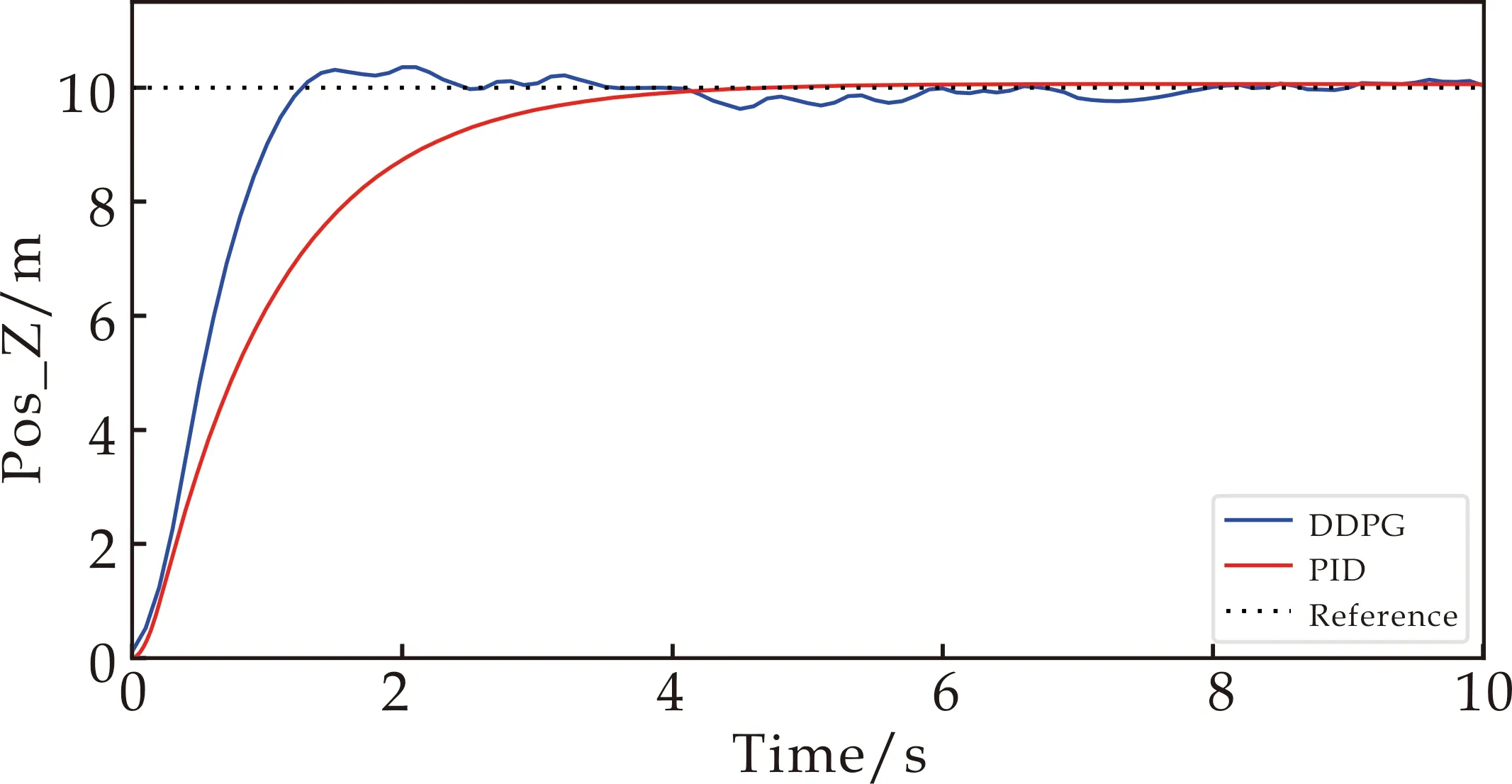
图5 DDPG策略和PID控制器的位置控制响应性能
为验证控制系统的有效性,本文设置了两个不同的目标高度进行测试.其余的任务设置保持不变,目标高度分别为[0,0,20]、[0,0,30].仿真结果表明,在不同的目标高度下,飞行器均能快速到达指定高度并保持悬停.高度通道的响应曲线如图6所示.
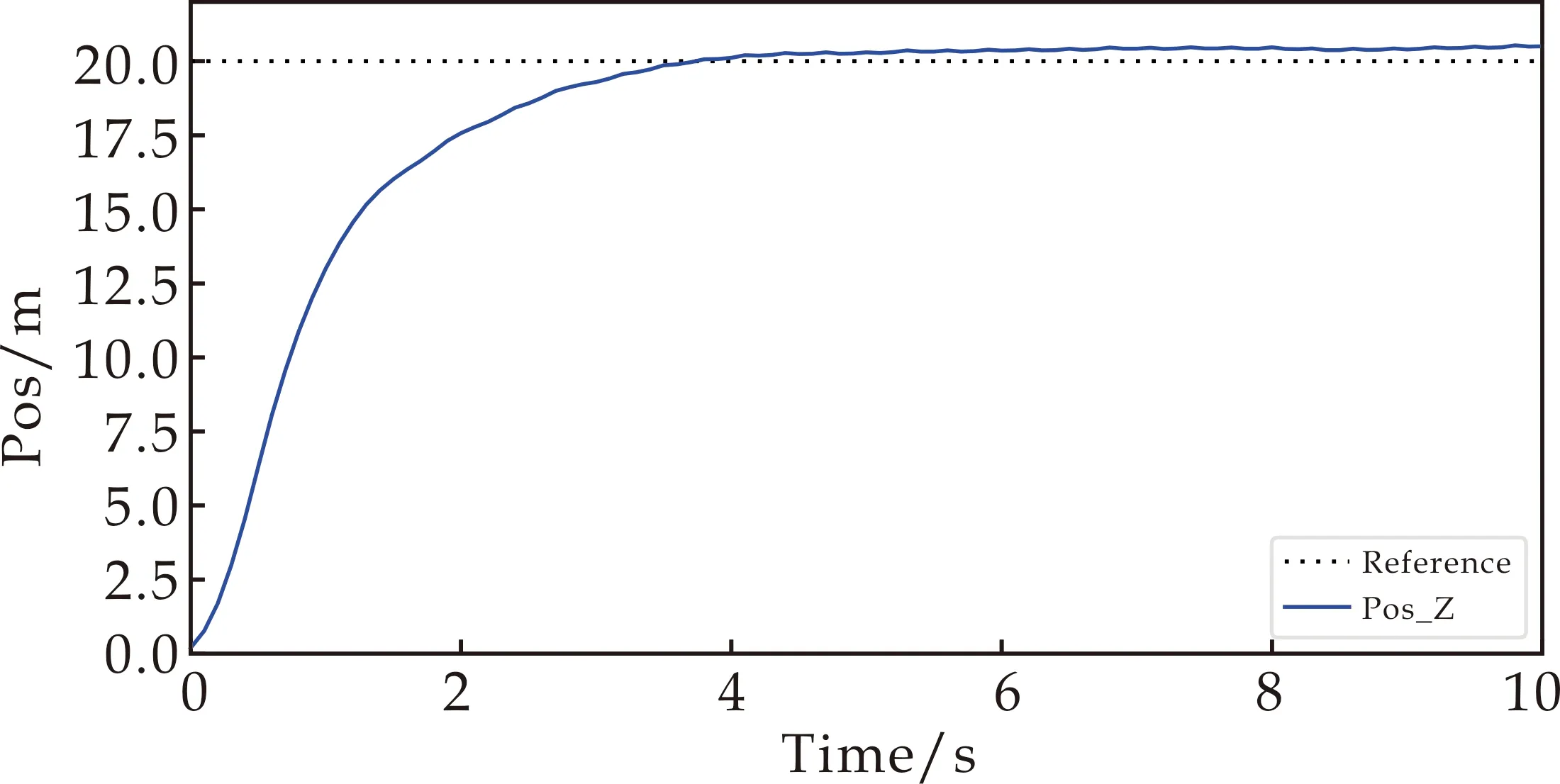
(a)目标高度为20 m
与其他强化学习算法相比,本文所提出的目标高度控制DDPG方法在稳态误差性能指标方面优于Tiwari等[16]提出的增强随机搜索(ARS)方法.分别使用两种算法设置相同的任务,初始位置[0,0,10],目标位置[0,0,150],目标高度控制性能对比如表4所示.由表4可得,在相同控制任务下,本文所使用的DDPG算法在进行目标高度控制时,高度的稳态误差更小.

表4 控制器性能分析
3.3 训练结果泛化能力测试
四旋翼飞行器的位姿控制最终是要将控制策略运用于真机飞行.因此,模型的泛化能力和鲁棒性尤为重要.本节主要研究对于不同质量以及不同臂长的四旋翼控制策略的泛化能力.使用目标高度控制任务进行模型泛化能力测试,将四旋翼从初始位置[0,0,0]驱动到目标高度[0,0,10]处并悬停.
质量对四旋翼飞行器的影响尤为显著,因为在实际飞行中,经常会给四旋翼飞行器加负载,如添加摄像头等.本文通过逐步给四旋翼飞行器加负载的方式探究控制策略对于质量的泛化能力.在固定其他参数不变的前提下,分别对整体质量为0.958 kg、1 kg、1.1 kg的四旋翼进行目标高度测试.不同负载的四旋翼飞行器训练效果如图7所示.
在固定其他参数不变的情况下,对臂长进行泛化能力测试.将四旋翼的臂长L分别增大和减小25%对四旋翼飞行器进行目标高度控制任务,四旋翼飞行器的臂长分别为0.3 m、0.4 m、0.5m.不同臂长的四旋翼飞行器的目标高度控制如图8所示.
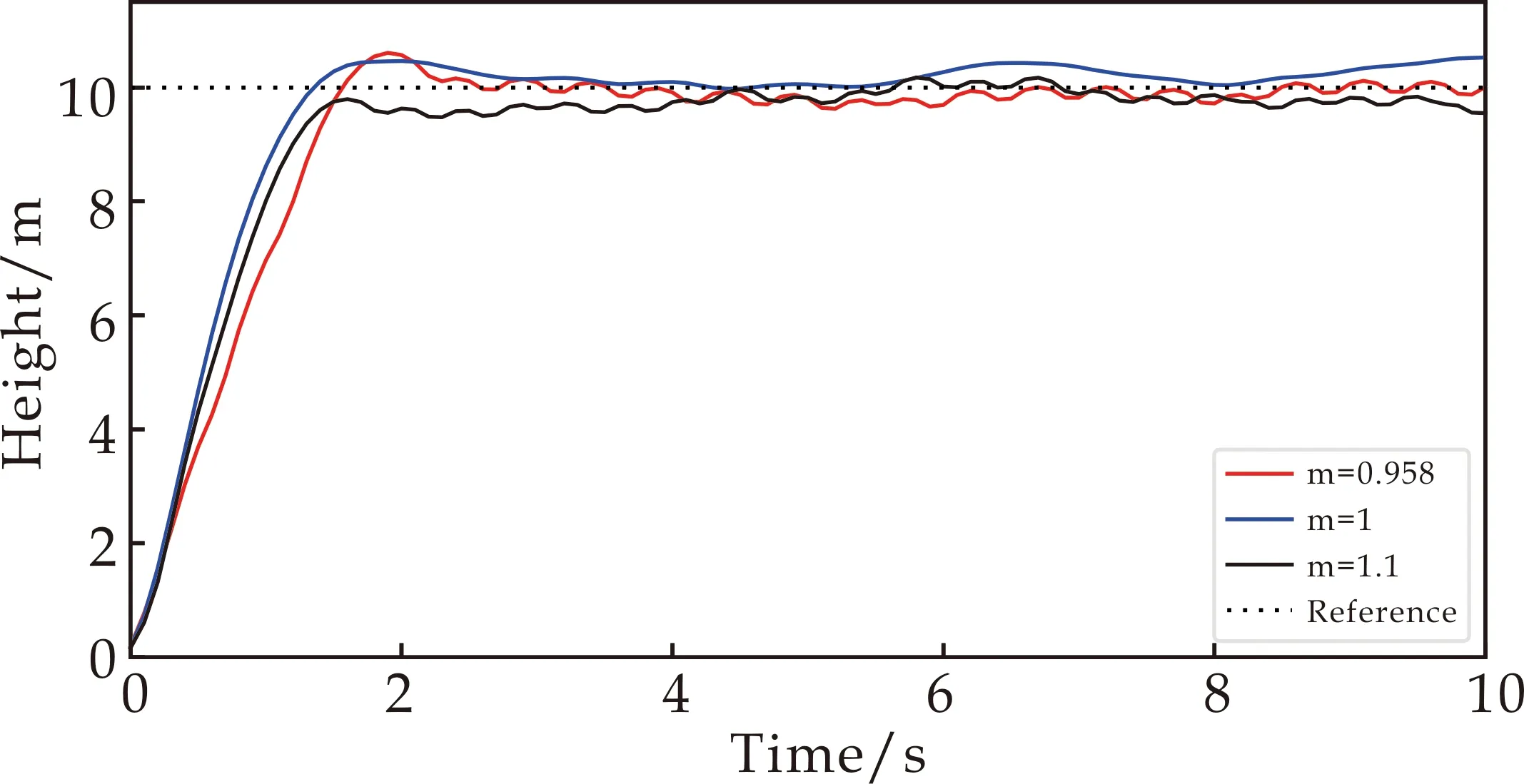
图7 四旋翼飞行器质量泛化能力测试
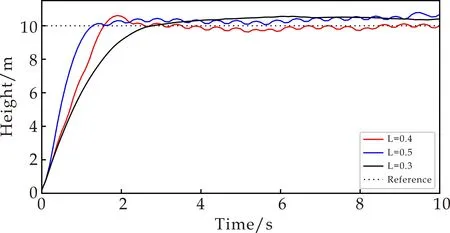
图8 四旋翼飞行器臂长泛化能力测试
从图7~8可以看出,在固定其他参数,仅改变四旋翼飞行器质量参数以及臂长参数的情况下,各通道的响应曲线没有太大变化,控制策略始终能完成四旋翼飞行器的目标高度控制任务,并实现悬停.通过对质量、臂长的泛化能力测试,说明深度确定性策略梯度算法在四旋翼飞行器目标高度控制方面具有鲁棒性.
4 结论
(1)本文基于回报函数塑造(reward shaping)理论,设计了一个新颖的体现越界惩罚的奖励函数,解决了飞行器易陷于环境边界的问题.利用深度确定性策略梯度算法实现了四旋翼飞行器的目标高度及悬停控制.该策略响应速度快于PID算法.与增强随机搜索(ARS)算法相比,该策略在高度上的稳态误差更小.
(2)在质量、臂长方面对本文的控制策略进行了泛化能力测试,验证了该策略的有效性与鲁棒性.
