基于响应面法的油气润滑ECT传感器优化设计

2021-12-01孙启国李照威

计算机测量与控制 2021年11期

孙启国,孙奥,李照威

(北方工业大学机械与材料工程学院，北京 100144)

0 引言

电容层析成像技术(ECT，electrical capacitance tomography)是一种工业过程层析成像技术。ECT系统主要由电容传感器、数据采集装置和计算机构成，其工作原理是被测物体具有不同的介电常数从而导致电容发生变化，其特点是价格低廉，非侵入式，响应速度快，成像过程无干扰[1-2]。目前，此技术被广泛应用于在多相流识别。

ECT传感器的结构将直接影响测量电容的采集和灵敏度的分布，进而影响重建图像的质量。目前，针对大管径(直径20 mm以上)的结构参数优化问题进行了较为广泛地研究。如文献[3]推导了电容敏感阵列电极的数学模型，根据灵敏度场确定优化指标，分析了结构参数对优化指标影响,并获得了一组结构优化参数。结果表明结构优化参数可靠，电容阵列敏感电极分辨率提高了10%。文献[4]设计了一种具有8个电极的ECT传感器，根据敏感场的均匀程度对传感器的参数进行选取，采用正交设计法对参数进行计算及优化，得到一组优化参数，结果表明优化后电容传感器可以获得较为理想成像结果。文献[5]建立了12电极的矩形ECT传感器，通过有限元法计算了电容极板和屏蔽极板长度对灵敏度分布的影响，提出了最佳电容极板长度应该与传感器的宽度或直径相同。文献[6]为研究管内为油水两相流设计了12电极的ECT传感器，根据灵敏度的均值和标准差确立了评价函数，改变单一结构参数对电容值重新计算，并结合正交实验法对4个参数进行优化。文献[7]采用遗传算法与响应面法结合的优化方法对电容传感器的相关结构进行优化，结果表明该方法有效，可以获得更佳的灵敏度分布。文献[8]根据仿真得到电容极板间敏感场的分布情况，基于PSO与混沌搜索策略理论提出了一种改进算法，以敏感场中的灵敏度大小为目标，并结合上述算法对ECT传感器结构进行优化，结果得到一组最优结构。文献[9]设计了一种三维结构的ECT传感器，研究了电容极板长度对灵敏度和图像重建的影响，提出了一个优化的三维ECT传感器设计，即电容极板的长宽比为0.75。文献[10]分别以均匀性指标和图像误差为目标对传感器结构进行分析，提出一种模糊综合指标作为优化目标，并结合正交法进行优化设计，结果表明优化后的传感器可以同时获得更好的灵敏度分布和图像重建结果。然而，目前对于油气润滑小管径(直径10 mm以下)有关结构参数优化的研究较少。

油气润滑ECT传感器尺寸较小，它对测量电容值、灵敏度场和重建图像质量的影响更加突出。本团队曾对油气润滑ECT传感器的二维结构的主要参数进行过优化设计，但考虑的优化参数较少，并且没有考虑其三维结构参数导致的特定影响。例如在小管径下，径向软场效应更加明显，管道电容和边缘电容不可忽略，这都导致传感器的灵敏度分布不均，测量电容值不准确，图像处理病态严重[11]。

针对以上问题，本文在二维结构参数的基础上，建立了UMIST型油气润滑ECT传感器的基准三维物理模型；分析了管道厚度、电容极板长度、轴向屏蔽电极长度和径向屏蔽电极深度4个结构参数对传感器性能的影响并确定优化范围；通过灵敏度影响系数和电容响应比确立了传感器性能优化函数；采用响应面法对上述4个结构参数进行了优化设计。最后以图像相对误差和图像相关系数为评价标准，对优化后传感器的重建图像质量进行评判以验证其可靠性。

1 油气润滑ECT传感器模型建立与结构参数分析

ECT传感器结构变化会影响正问题中的测量电容值和灵敏度场分布，进而影响反问题中的流型识别和图像重建质量。本文首先以UMIST型的ECT传感器作为基准传感器，并计算测量电容值，然后在基准传感器上改变单个结构参数值，重新计算测量电容值，最后通过比较满场/空场电容差的大小来判断传感器性能变化，从而确定结构参数的优化范围。

1.1 物理模型建立

ECT传感器通常采用低频激励，即小于1 MHz，其内部可视为静电场。在油气管道中只考虑环状流，建立基准传感器。基准传感器从外到内的构成为外屏蔽罩、轴向屏蔽电极、电容极板、径向屏蔽电极、管道，如图1所示。图2给出了其径向管道二维视图，图中极板张角为θ，径向电极插入深度为h1，管道圆心到管道半径距离为R1，管道圆心到管道外径距离为R2，管道圆心到外屏蔽罩距离为R3，其具体结构参数，见表1。

图1 基准传感器的结构图

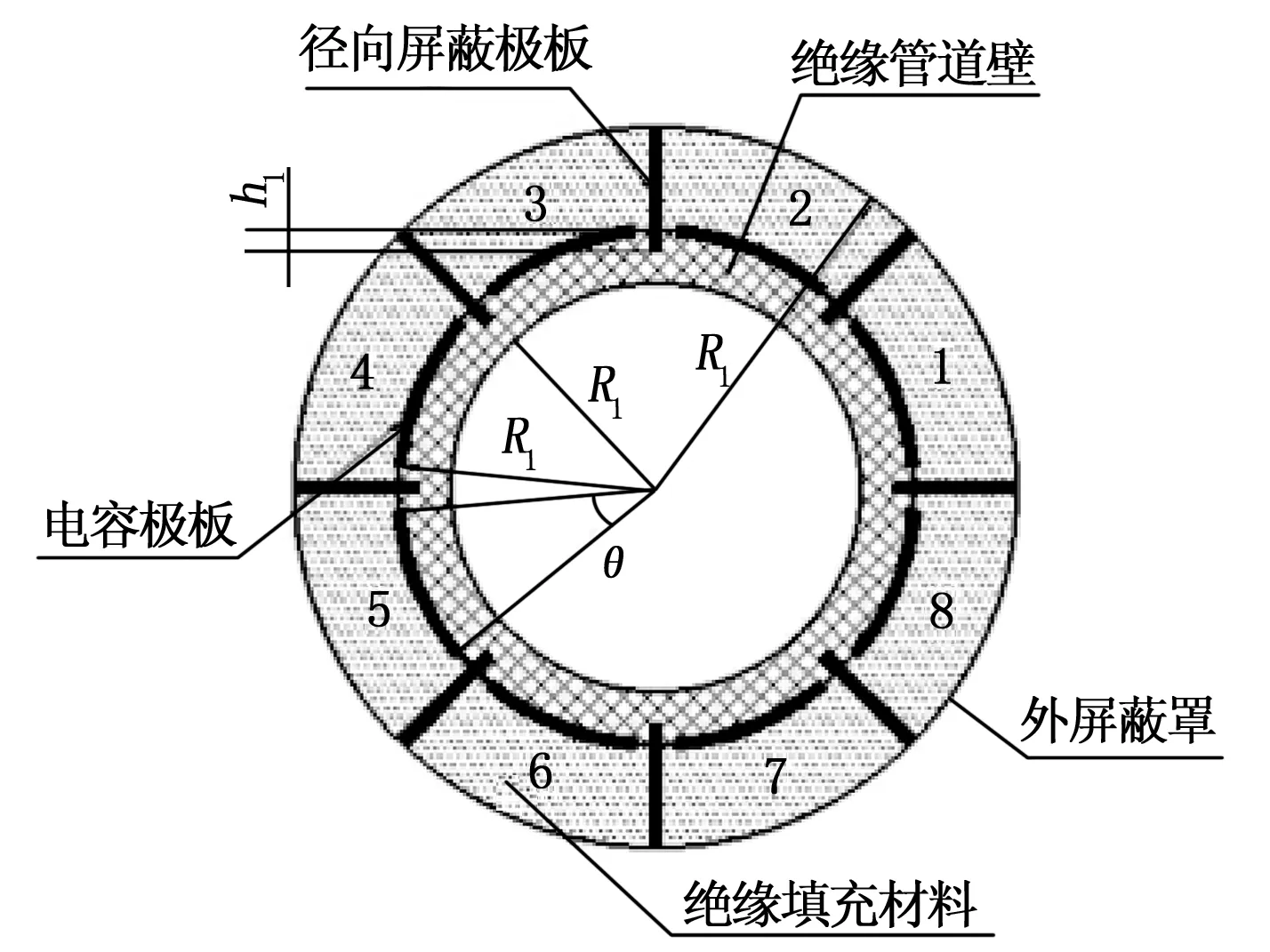
图2 径向管道二维视图

表1 基准传感器的结构参数

1.2 数学模型建立

为了求解ECT模型的电容值及其灵敏度，对三维模型做以下假设:1)各相介质分布均匀且互不干扰；2)屏蔽罩隔绝外部电场；3)管道内无自由电荷。

根据以上假设，电势分布可以用泊松方程可以表示为[12]：

▽·[ε(x,y,z)▽φ(x,y,z)]=0

(1)

式中，▽·及▽分别为散度及梯度算子，ε(x,y,z)相对介电常数分布，φ(x,y,z)为三维电势分布。

以8电极传感器为研究对象，若激励电容极板为i，狄里赫利边界条件为：

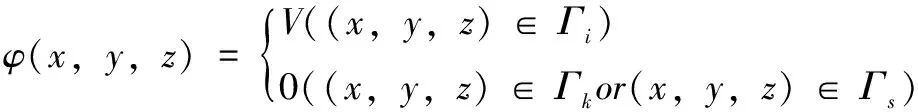
(2)

式中，k=1,2,...,8且k≠i，V为极板激励电压，Γi为激励极板表面，Γk为检测极板表面，Γs为径向屏蔽极板和屏蔽罩表面。

对一端的电容极板i施加电压V，另外一段的电容极板j由于电势差就会产生相应的电荷，根据高斯定理可得极板j的电荷量，则i，j俩极板之间的电容可以表示为：

(3)

式中，Q(Γj)为电极j上的感应电荷量，Γj为在极板j周围的封闭区域。

在第i和第j电容极板间的灵敏度可以表示为：

(4)

式中，p(x,y,z)为(x,y,z)的体坐标点；Ei(x,y,z)，Ej(x,y,z)为i极板激励，j极板接地时，在(x,y,z)处的电场强度。

1.3 结构参数分析

本文对管道厚度，电容极板长度，轴向屏蔽电极长度，径向屏蔽电极深度4个结构参数进行分析。由于油气润滑ECT传感器的对称性，只求解电容极板1与电容极板2、3、4、5间的测量电容及电容变化量。改变结构参数的测量电容值如表2所示，其中满场为管道内全为润滑油，空场为管道内全为空气。由表2数据可以看出，当ECT传感器的结构发生改变，电容极板间的测量电容值也会发生变化。

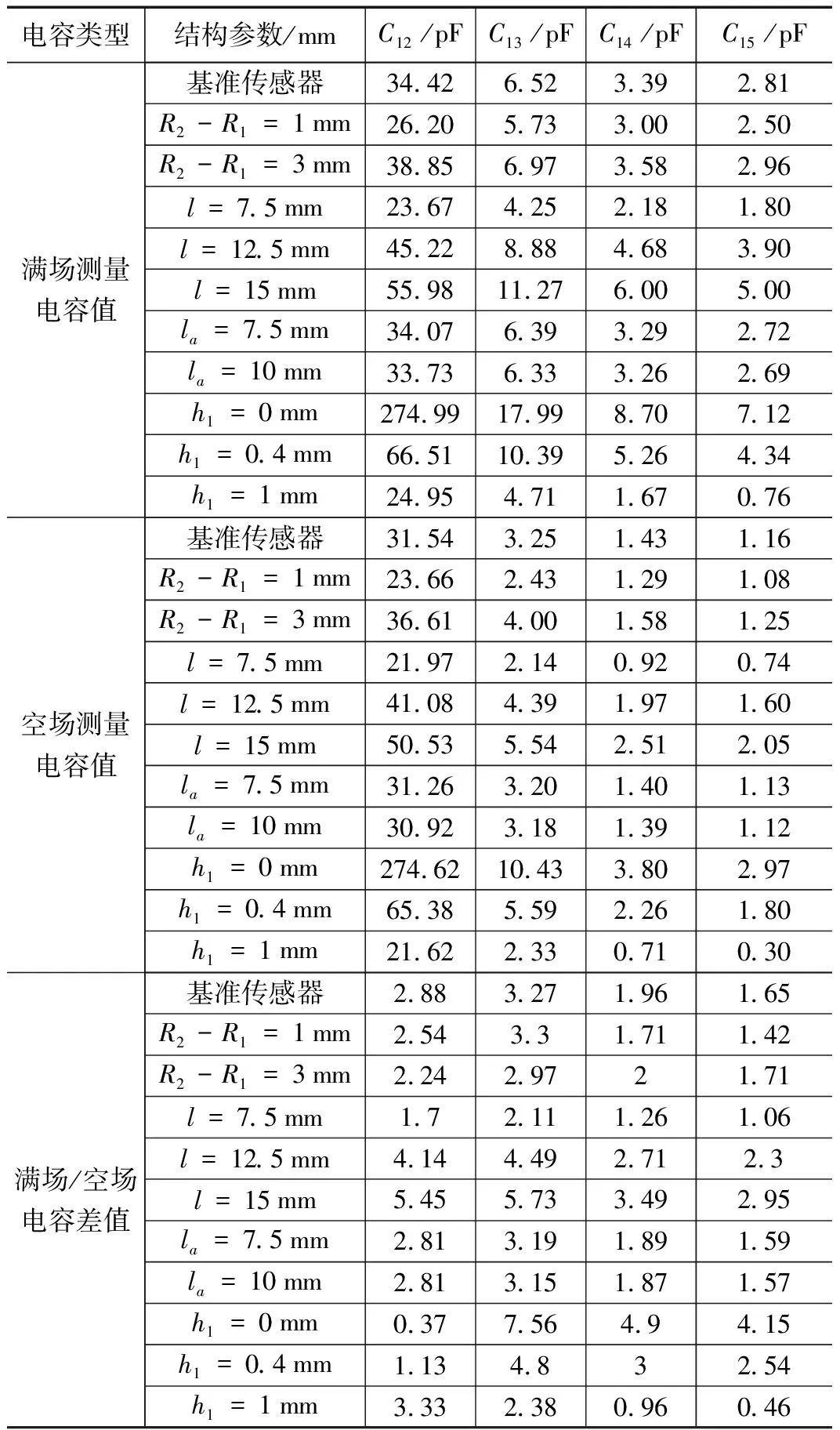
表2 改变结构参数的测量电容值

满场测量电容值与空场测量电容值的差值反映了传感器对管内整体单元的敏感程度，其差值越大，说明传感器对管道内多相流变化越敏感，性能越好[13]。因此，本文用满场/空场电容差值来评价传感器性能。

各结构参数分析如下。

1)管道厚度R2-R1：管道厚度越大，满场和空场的测量电容值越大，数据采集越容易，但由于油气润滑系统的管道较小，管道电容对测量电容有一定影响，即减低测量电容值的准确性，减低管道厚度可以减小管道电容对测量电容的影响，即提高测量电容值的准确性，故管道厚度的优化范围不宜太大。从表2可以看出，随着管道厚度不断增加，满场/空场电容差值中的C12、C13不断减小，C14、C15不断增加，可见满场/空场电容差值整体变化并不明显。综合考虑油气润滑管道厚度的优化范围在R2-R1∈[1,3]比较合理。

2)电容极板长度l：电容极板越长，其有效面积增加，管内所包含的介质越多，测量的电容值越大，但会出现三维弱化现象，不能很好地反应管道内多相流的分布。电容极板越短，其有效面积减少，虽然能很好的反应管内不同相的分布，但测量电容变得较小，这增加了数据采集的难度。由表2可以看出，电容极板长度越长，满场/空场电容差值越大，但增加的趋势不明显。故电容极板长度的优化范围为l∈[10,15]。

3)轴向屏蔽电极长度la：油气润滑系统中，边缘电容影响系数超过0.5，即轴向的边缘电容也会影响测量电容值[14]。轴向屏蔽电极不但可以消除边缘电容，提高测量电容的准确性，而且可以提高传感器管道内部灵敏度场的均匀性。由表2可以看出，轴向屏蔽电极长度对满场/空场电容差值影响不大，故轴向屏蔽电极长度优化范围为la∈[5,10]。

4)径向屏蔽电极深度h1：径向屏蔽电极主要作用于相邻电容极板对之间，它可以阻断相邻电容极板间的电场线，使相邻电容极板对间的测量电容降低。由于非相邻电容极板对间的电场线主要经过管道空间，所以径向屏蔽电极对其影响不大。由表2可以看出，随着径向屏蔽电极深度的增加，相邻电容极板对的满场/空场电容差值不断增加，但非相邻电容极板对的满场/空场电容差值不断降低，综合加工工艺问题，故径向屏蔽电极深度的优化范围为h1∈(0,1]。

2 油气润滑ECT传感器优化实验

2.1 优化函数的确定

油气润滑ECT传感器中，由于“软场效应”导致管道内部的灵敏度分布不均匀，即管道外侧靠近电容极板的位置传感器的灵敏度高，而在管道中心传感器的灵敏度相对较低，进而导致重建图像的质量不佳[15]。因此。优化传感器的一个重要指标是让其管道内部具有均匀相等的灵敏度。油气润滑ECT传感器具有8个电极，由于对称性，典型的灵敏度场只有4个，即1-2，1-3，1-4，1-5。本文定义灵敏度影响系数P：

(5)

(6)

(7)

(8)

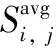
P值越小，表示油气润滑ECT传感器中的灵敏度场分布越均匀。

在油气润滑ECT传感器中，测量电容值的准确性是影响图像重建质量的另一重要指标。在管道内为环状流的情况下，相邻电容极板对间的测量电容值最大，表示为：

(9)

相对电容极板对间的测量电容值最小，表示为：

(10)

本文定义电容响应比，表示为：

(11)

电容响应比Cr值越小，说明传感器所需的量程范围低，测量的电容值越准确。

综上所述，油气润滑ECT传感器的优化设计需要同时考虑灵敏度和测量电容值这两个方面的指标。因此，本文定义油气润滑ECT传感器的性能优化函数，权值系数都为1，结合公式(5)和(11)表示为：

ySOF=P+Cr

(12)

可见，综合优化函数ySOF值越小，油气润滑ECT传感器的性能越好。因此，本文将优化问题转化为求ySOF的最小值。灵敏度和测量电容值是通过有限元仿真计算得到的，与传感器的结构参数并无明显的数学表达式，因此需要采用一定的优化理论建立数学关系。

2.2 响应面法实验设计

响应面法(RSM，response surface method)综合了数学建模和实验设计，首先通过对少量且具有代表性的样本点进行实验，然后回归拟合并建立所需因素和结果的函数关系，最后根据实验者的需要取得所需因素的最优水平值。近年来成为发展最快的优化理论方法，多用于医学制药，环境工程，机械工程等领域中各种因素的优化设计[16]。

响应面法的基本方法是运用线性或者多次方程来拟合未知复杂的函数。它与正交实验相比，正交实验不能在选取区域内获得样本点的最优组合，从而无法得到响应目标的最优解。而且当有较多实验因素时，正交实验次数会极大增加，增加工作量。响应面法的优势明显，例如拟合精度高，实验次数和周期短，预测效果好等[17]。

一般情况下系统响应Y与影响因素x之间关系可以表示为[18]：

(13)

实验值与响应值通过响应面法拟合的目标函数可以表达为：

(14)

式中，β0为偏移系数，βi为待定系数，φi(x)为基函数，k为基函数的个数。

在能满足目标函数的要求下，设计的响应面函数要尽量简单。本文优化参数较多为非线性问题，因此采用二阶响应函数，表达式为：

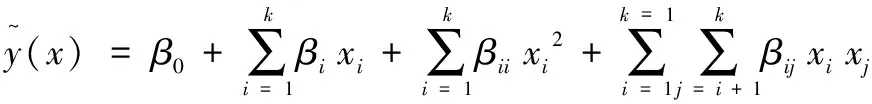
(15)

式中，βi为一次项系数，βii为二次项系数，βij为交互项系数。

本文影响因素为4个，因此采用Box Behnken Design(BBD)方法确定油气润滑ECT传感器的设计优化方案。BBD实验点分布如图3所示。BBD设计法中每个影响因素有3个水平，水平从小到大分别以-1，0，1对其编码,即-1代表最小值，0代表中间值，代表最大值。各个影响因素水平值和编码值如表3所示。

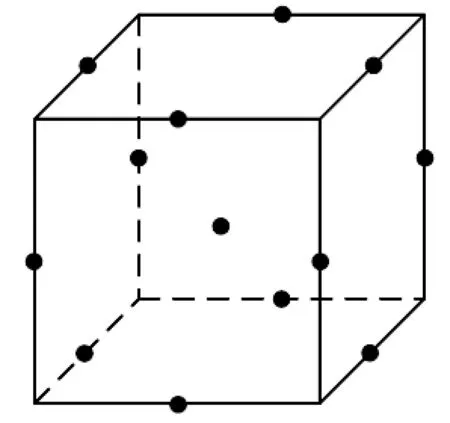
图3 BBD实验点分布

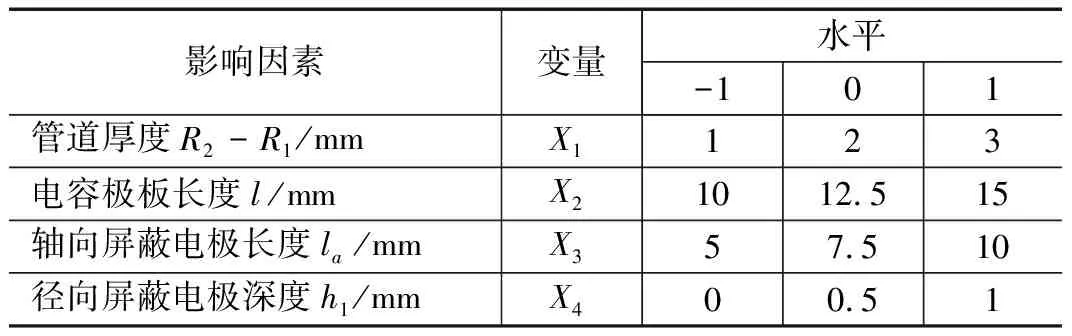
表3 影响因素的水平值和编码值

2.3 实验结果分析

根据表3可自动生成结构参数组合，再通过仿真计算和数据处理可以得到性能优化函数值(ySOF)，最后结合响应面实验对4个参数进行综合考虑并优化。响应面实验具体数据如表4所示。

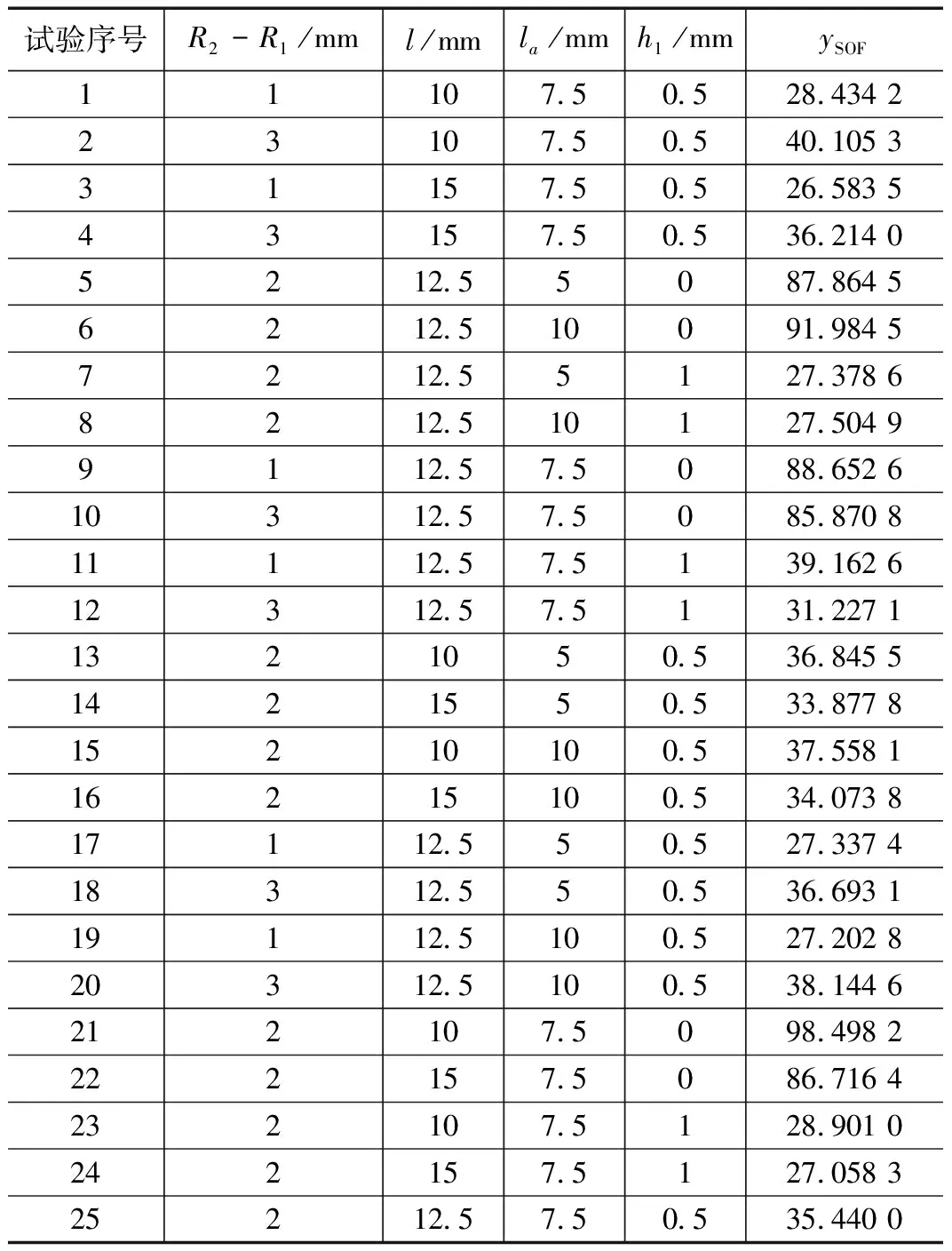
表4 响应面实验具体数据

拟合出来的回归方程需要进行误差分析，以判读回归方程的拟合程度。残差概率分布几乎在一条直线上，说明回归方程拟合效果好[19]。残差概率分布如图4所示。

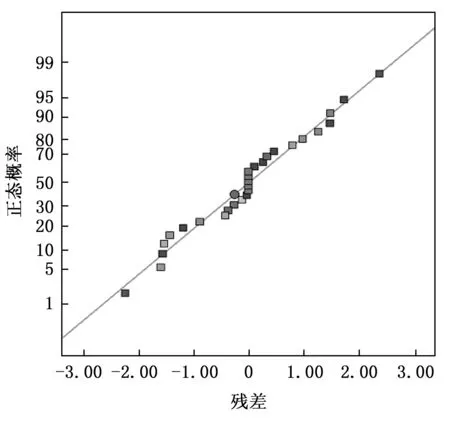
图4 残差概率分布

由图4可知，本次拟合的回归方程精度高，适应性较好，可以对油气润滑ECT传感器的影响参数进行优化预测。根据预测功能选取ySOF值最小的一组参数组合。优化参数组合如表5所示。

表5 优化参数组合

3 油气润滑ECT传感器优化结构验证

本文采用LBP和Tikhonov正则化算法对基准传感器和优化后的传感器进行图像重建，并通过图像相对误差(IME，the relative error of image)和图像相关系数(CORR，the image correlation coefficient)来比较图像质量。

IME和CORR表达式分别如下[20-21]：

(16)

(17)

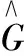
本文对管内所有像素点进行计算。图像相对误差(IME)反应了重建图像与真实图像误差大小，其值越小越好。图像相关系数(CORR)反应了重建图像与真实图像的相关程度，其值越大越好。IME和CORR值如表6所示。

表6 IME和CORR值

由表6可以看出，基准传感器的图像相对误差平均为0.632 3，优化传感器的图像相对误差平均为0.402 4，相比基准传感器的图像相对误差平均降低了22.99%；基准传感器的图像相关系数平均为0.710 6，优化传感器的图像相关系数平均为0.927 9，相比基准传感器的图像相关系数平均提高了21.73%。可见，采用优化传感器得到的重建图像质量更高。