基于AHP、灰色关联法和TOPSIS的航天测控装备评估模型研究
2021-12-01朱东济蔡红维欧阳霄
朱东济,蔡红维,欧阳霄,仝 非,杨 辉
(1.西昌卫星发射中心,四川 西昌 615000;2.中国航天员科研训练中心,北京 100094)
0 引言
随着北斗二代导航卫星、嫦娥探测器、空间实验室等建设需求的增多,发射场的火箭发射也急剧增多,我国2020年全年39次航天发射任务[1]。测控系统承担着运载火箭发射弹道测量、遥测、遥控等任务,长期处于工作状态,测试维护的时间和周期越来越少[2-3],这就要求在平时和工作中及时掌握装备的性能状态。由于测控系统有着设备种类多、复杂度高、参数指标杂、地域分布广等特点[4-5],评估难度较大。而且,当前评估方法追求超前的理念和复杂的算法,评估方法种类繁多、评估理念层出不穷[6]。所以,目前发射场测控系统性能评估主要靠岗位人员主观进行分析和评判,受人员知识能力、技术水平和经验等因素制约,还没有成熟、客观、全面的性能量化评估系统。
本文结合发射场测控系统的上述特性,以符合具体的应用环境、以实用为导向,提出了一种采用传统AHP层次分析法、灰色关联分析法和TOPSIS法的组合模型,从指标体系建立到量化分析、再到评估结果输出,构建了一套完整的数学处理方法用来评估测控系统的装备性能,并选取具有代表性的某型单脉冲雷达发射机分系统为例,验证了该方法的可用性、合理性、有效性,在实际中取得了较好的效果。
1 评估思路与流程
AHP层次分析法是一种对系统进行层次建模的方法,该方法由于契合了事物的层次特点,目前已经应用于很多领域很多方面。每个系统都有各自的指标参数,这些指标从不同方面表征了系统性能,而这些指标可能各不相属又紧密关联,彼此之间即有区别由有联系,这契合了层次分析法的根本思想。采用层次分析法不仅便于梳理系统存在的指标,还可以对指标进行分析比较,最终能够获取各个指标在系统中的权重[7]。测控系统尽管由各种不同种类的不同功能的装备组成,但都具有典型的层次结构[8]。在建立问题的评价指标体系时,采用AHP层次分析原则,契合了测控系统的层次结构,更有助于评估指标体系的梳理确定;对于测定指标数据,指标的维数和样本量往往没有严格的要求,不知道具体的分布特性,很难判定系统是“好”是“坏”,界限的确定不易分辨,而这正是灰色分析要解决的问题。1982年我国学者邓聚龙教授提出了灰色系统理论,其主要思想就是利用掌握的系统信息对系统进行“非此即彼、非好即坏、非黑即白”的情形评价;对系统的样本数据也没有严格的要求,拓宽了其应用范围,目前已经形成了比较完备的理论体系[9]。灰色关联度分析作为其中一种多因素统计分析方法,用灰色关联度来表征因素间关系的大小顺序或强弱关系,综合灰色关联度,形成灰色关联系数,以反应各评价对象对基准或参考对象的接近次序[10-11];对于所有的关联系数求和平均即绝对关联度,显然不是一个理想的方法。采用Yoon和Hwang开发的接近理想方案的相对接近程度的序数偏好方法TOPSIS,具有方案信息使用较充分,丢失较少的优点[12]。所以,为了更好地体现方案数据曲线位置上的关系,从而能够集中反映方案决策信息的总体情况,对灰色关联系数进行数值比较,可以对整体的偏好程度进行清晰明了的排序[13-14]。采用AHP、灰色关联法与TOPSIS综合评估的流程包括从指标体系构建→权重量化→指标量化→分析评估→结果确认的全过程,如图1所示。

图1 综合评估流程
2 评估过程
2.1 AHP模型的构建
每一个要评价的对象都应该有反应自身特性的一系列、甚至一大堆指标,这些指标即区别又联系,应具有反应评价对象的充分性,能够从不同的方面反应评价对象的某种性能,体现出评价对象的优劣程度,进而所有这些指标的集合形成综合评价系统的指标体系[15]。指标体系的构建需要一套全面严格的评估规范、评估程序、评估标准[16-17]。雷达是担负导弹航天发射测控的重要设备,选取某型单脉冲雷达作为代表,梳理发射机系统指标层次关系[18]:目标层为根目录,即发射机分系统;准则层为波形参数、频谱特性、输出功率、钛泵电源、水冷状态、高压电源、充气组合和调制器等8个并列单元;方案层以脉冲前沿、脉冲后沿、顶降,杂散分量、谐波分量,峰值功率、功率稳定度,收集极电流、管体流量、输出窗流量、温度,高压电源输出电压、电流,高压脉冲电压、电流等15个子科目作为最低层。钛泵电源和充气组合准则层由于不能再分下级科目,可直接引申至三级,这样便于底层指标数据的统一处理。整体层次关系如图2所示。
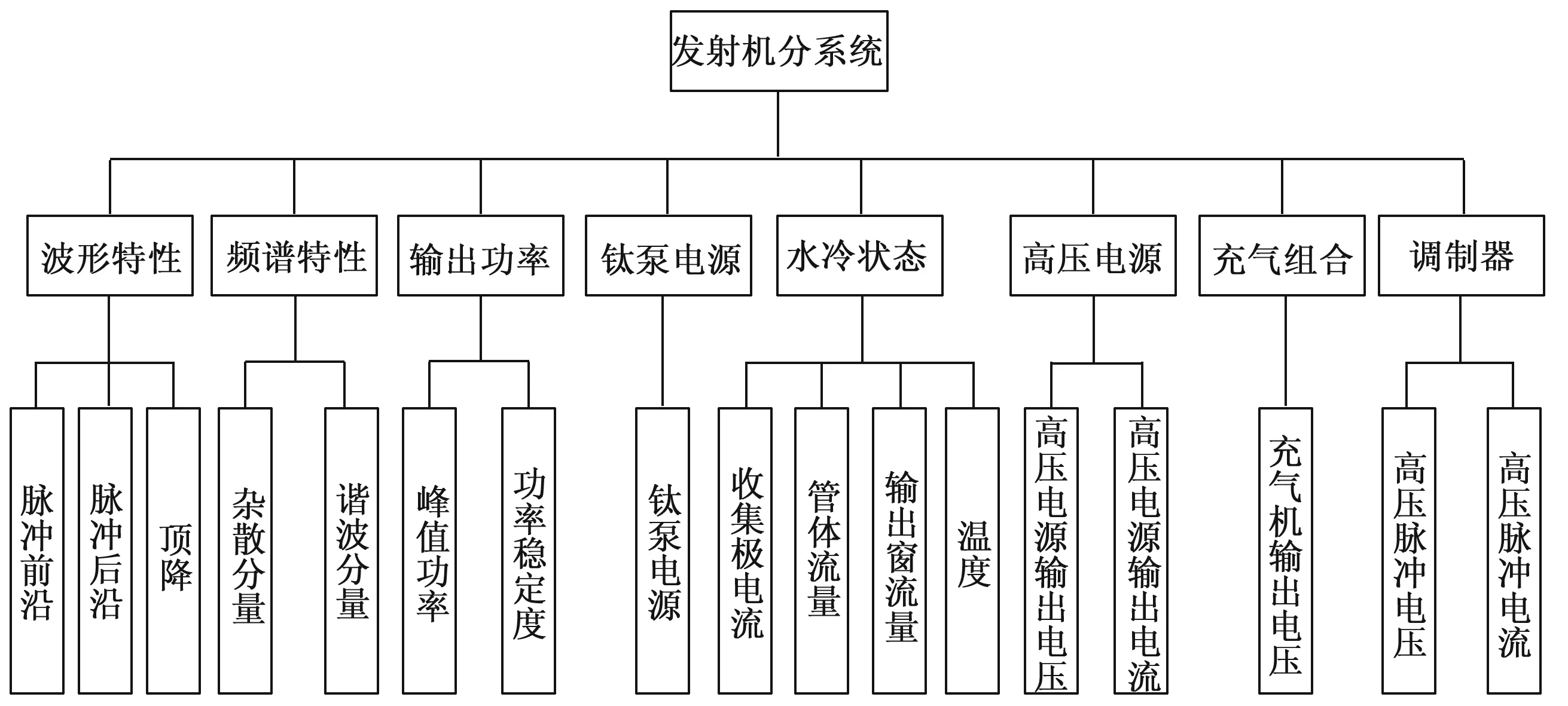
图2 某型雷达发射机分系统层次关系模型
2.2 判断矩阵的构造与赋值
利用图2构造的AHP模型形成判断矩阵即利用层次关系构造判断矩阵,同一层次的参数按相应的行和列进行排列,如第二层8个参数,可构造8×8矩阵,第三层水冷状态参数可构造4×4矩阵。矩阵数值引用数字1~9及其倒数作为标度[19],表1列出了1~9标度的含义。

表1 1~9标度的含义
表中只给出了奇数的含义,但它们之间的数2、4、6、8及各数的倒数具有相应的类似意思。
2.3 层次模型权重的确定
利用上文构造的赋值型矩阵计算模型的权重,即从数值矩阵出发,计算矩阵的最大特征根λmax,进而求取对应的特征向量W,W即为层次模型的权重。计算矩阵最大特征根λmax及特征向量W方法不一,但都大同小异,区别只是在计算精度上不同而已。由于和积法计算采用近似方法计算比较简化,又能保证足够精确度,这里采用了和积法的计算步骤,详细演示了计算AHP权重的过程,具体如下。
1)将判断矩阵每一列正规化:
(1)
2)将每一列正规化后的判断矩阵按行相加:
(2)
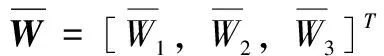
(3)
所得到的W=[W1,W2,W3]T即为所求特征向量。
4)计算判断矩阵最大特征根λmax:
(4)
式中,AWi表示向量AW的第i个分量。
5)判断矩阵的一致性检验:
由于判断矩阵是以人的主观认识构造的,为了防止矩阵的不合理性,需要对矩阵进行一致性检验,计算它的一致性指标CI,定义:
(5)
若CI=0,则判断矩阵完全一致。λmax-n越大,一致性越差。进一步将CI与平均随机一致性指标RI进行比较,RI分别如表2所示,则可获得满意的一致性。

表2 RI平均随机一致性指标
对于1阶、2阶判断矩阵,矩阵关系明确,一致性检验意义不大,所以总是完全一致的;当阶数大于2时,如果判断矩阵的CR=CI/RI<0.10时,则其具有满意的一致性,否则就需要重新对判断矩阵赋值。通过一致性检验的向量特征向量W才能确定为层次权重。
2.4 TOPSIS分析
1)分析指标数据,建立决策矩阵。TOPSIS法从n个属性和方案两个维度形成评价的决策矩阵,属性可视为对象即雷达的层次关系、方案视为一组指标的具体数据。
(6)
2)确定矩阵的正基准、负基准、参考基准。令两个假设的方案A+和A-定义为:
(7)
式中,J为效益型属性集合,J′为成本型属性集合。方案A+和A-分别表示正基准和负基准的方案。
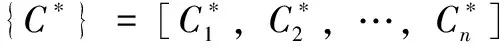
3)计算灰色关联系数:
用关联分析法计算矩阵矩阵灰色关联系数,第i个方案第k个指标与第k个最优指标的关联系数ξi(k)为:
(8)
式中,ρ∈[0,1],一般取ρ=0.5。
由式(3)得到权重W,由式(8)计算关联系数ξi(k)矩阵:
此模块实现五类题型的管理功能。试题类型分别为单选题、多选题、判断题、填空题和问答题。根据需要对指定的课程的试题进行录入、更新和删除操作。本模块是考试系统的主要功能模块。由于科技的进步,知识会不断创新,教师可根据课程内容和知识的更新,定期不定期的对题库中的试题进行编辑(包括增加、修改等)操作,便于对题库及时更新,保证了考试时所组的卷与教材和所学的知识同步。
vi=W(k)×ξi(k)
(9)
4)计算距离:
计算每个方案的距离,通过多维Euclid距离来测量。每个方案与正基准方案的距离为:
(10)
同理,与负基准方案的距离为:
(11)
5)计算相对基准解的接近度。Ai与A+的相对接近度定义如下:
(12)
依据Ci+的降序,排列偏好顺序。
3 评估实例与分析
3.1 雷达AHP模型分析
由图1可知,以发射机分系统为根目录,其下的层次有8个并列单元,对这8个单元按行和列排列,由式(1)形成8×8矩阵,如表3所示;同理,以水冷状态参数这一层为目录,其下有4个并列单元,对这4个单元也按行和列排列,形成4×4矩阵,如表4所示。对于4阶以下的矩阵,由于单元关系简单明了,直接采用专家赋权法。
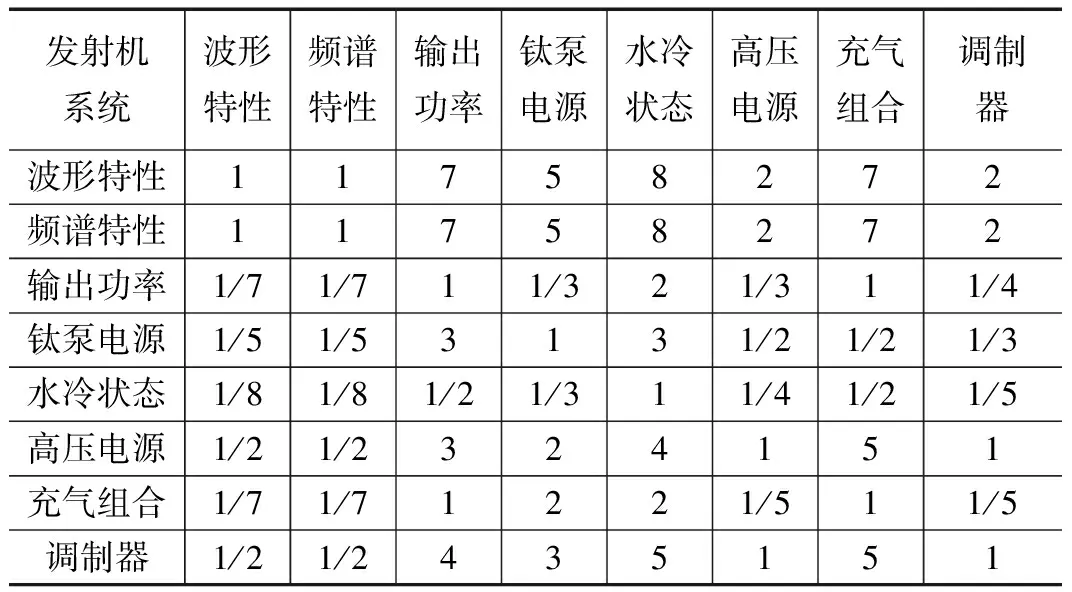
表3 发射机准则层判断矩阵

表4 水冷状态判断矩阵
3.2 雷达AHP权值计算
式(1)~(5)的计算有特征根法、方根法、和积法、行和归一化法,仅有计算速度的区别,计算结果差异不大。本文采用和积法,计算结果如下:
4×4矩阵:特征向量=[0.052 86 0.211 65 0.211 65 0.523 84]T
λmax=4.073 849
CI=0.024 616
CR=0.027 352<0.10
8×8矩阵:
特征向量=[0.268 574 0.268 574 0.039 241 0.062 921 0.027 219 0.135 525 0.047 219 0.150 726]T
λmax=8.324 788
CI=0.046 398
CR=0.032 907<0.10
从权重(特征向量)、最大特征根、一致性指标等参数看,判断矩阵设置合理,权重计算结果一致性良好。用和积法计算发射机分系统得到的权重为第一层权重,水冷状态权重为第二层权重,第二层其它权重采用专家赋权法[20]。对应的的二层权重和相应的第一层权重对应相乘,得到最底层的权重W。
W=[0.268 574*0.5 0.268 574*0.3 0.268 574*0.2 0.268 574*0.5 0.268 574*0.5 0.039 241*0.5 0.039 241*0.5 0.062 921 0.027 219*0.052 86 0.027 219*0.211 65 0.027 219*0.211 65 0.027 219*0.523 84 0.135 525*0.5 0.135 525*0.5 0.047 219 0.150 726*0.5 0.150 726*0.5],AHP模型的权重量化如图3所示。

图3 发射机权重量化AHP模型
3.3 雷达指标参数归一化、灰色关联度
本文将正理想归一化为1、负理想归一化为0,并以正理想为参数数列。指标参数归一化、灰色关联系数,结果如表5所示。
3.4 综合评估结果
由式(10)~(12)可知,如果Ai=A+,那么Ci+=1;如果Ai=A-,那么Ci+=0。当Ci+趋近1时,方案Ai接近A+,据此计算表5中的序列综合结果,计算结果如下。

表5 发射机系统评价指标、归一化及关联系数ξi(k)
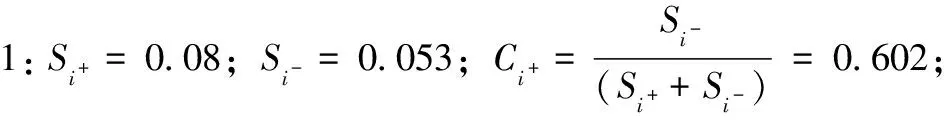

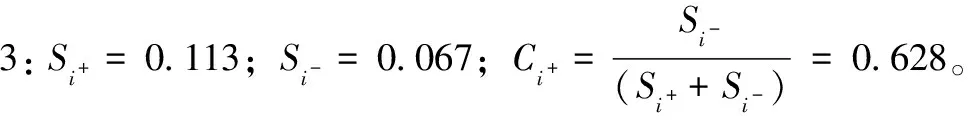
根据综合评判结果排序,序列3>序列1>序列2,所以序列3的量化评估效果比序列1的效果好,序列1的效果比序列2好。数值大小直观的互相比对,非常便于测试、联调、合练等过程效果的评估。例如,在测控系统联调中,当积累足够多的数据后还可以对联调等级进行更仔细的划分,从而对联调效果进行更精确的评估。综合评估方法,用AHP确定指标权重、将指标优劣中间的灰色地带转换成定量指标,用TOPSIS法进行最后的选择,避免了评估过程每个环节依靠岗位人员评估的主观性。
4 结束语
针对测控装备评估难的问题,采用AHP层次分析法进行指标体系的权重量化、灰色关联分析对多维指标参数进行分析处理、TOPSIS法进行灰度比较选择,从而建立起测控装备量化评估的综合模型;并以航天发射场具有代表性的某型雷达发射机分系统为例,验证了该模型的合理性、可靠性、有效性。采用AHP基于测控系统本身的层次结构,有利于指标体系的梳理和建立;采用灰色关联法针对测控系统装备参数多、指标差异大的特点,避免了岗位人员评估的主观性,能够比较客观、全面的评估系统性能;应用TOPSIS则能够对AHP和灰色关联结果产生清楚的偏好顺序。
采用该综合评估方法,可以解决航天测控装备性能量化分析难以及时、客观、全面评估的问题,但由于测控装备种类多、系统复杂度高,在将本文对单脉冲雷达的处理方法应用在其它设备时,还需要根据具体实际情况进行针对性的层次关系梳理、灰度关联和TOPSIS计算。另外,评估方法给出的结果可能和人为判断存在不一致的地方,这还需要根据相关人员的技术经验、知识水平等对方法不断完善和改进,才能更贴合于实际。
