双轴跟踪式光伏发电设备的风载仿真研究
2021-11-30沈胜伊董春颖
沈胜伊 董春颖
摘要:光伏发电设备的抗风能力对其安全性、使用寿命和制造成本有直接影响。目前,发电效率最高的光伏设备是二维跟踪式光伏发电设备。该设备始终跟踪太阳的方位和仰角运动,最大限度保证光伏板垂直于光照方向。跟踪式光伏发电设备比固定式结构更复杂,随着光伏板跟踪太阳旋转,所受风载也随之不断变化。本文主要研究:(1)采用有限元法进行流固耦合仿真,对不同姿态角的跟踪式光伏发电设备进行风载仿真。研究了风载随姿态角的变化规律,分析了特定姿态角产生最大风载的原因。(2)通过风力矩测量实验系统采集实验数据,对实测值和仿真值进行对比,验证上述仿真方法及结论的正确性。
关键词:风载荷,仿真分析,跟踪式,光伏发电
一.研究背景
双轴跟踪式光伏发电设备是本文的研究对象。它有两个回转轴,分别旋转跟踪太阳的方位和仰角,保持光伏板始终跟踪太阳运动,发电效率较固定式提高35%左右。它的最大跟日风速为14m/s,极限抗风风速为28m/s。
跟踪式光伏发电设备具有特殊的工作环境和跟日结构,由于该设备的光伏板一直跟踪太阳运动,所以风载荷最复杂。本文采用计算流体力学,以流体力学为基础,以数值计算为工具,对流动问题进行分析的方法。
目前,跟踪式光伏发电设备存在一些问题:减速器驱动扭矩过小,设计扭矩与实际工作扭矩不符。在大风天气下,减速器经常过载工作,需要定期维修减速器;
本文的研究目的是解决跟踪式光伏发电设备减速器容易过载工程实际问题,对该设备研发设计有工程指导意义。
二.风力和风力矩定义
风载荷作用在物体上的力一般可简化为风力和风力矩,根据坐标系可简化为3个力和3个力矩。参考天线结构风力体轴坐标系[1],本文建立以跟日减速器轴线为基准的体轴坐标系。对处于三维空间中的风力,通常用、和三轴分别表示空间中的风力方向。体坐标系的六个分量为:
轴向力,沿设备轴线方向;
横向力,沿设备轴线方向;
横向力,沿俯仰轴方向,与地面垂直;
翻滚力矩,力矩轴线与轴线一致;
俯仰力矩,力矩轴线与轴线一致,与俯仰减速器旋转轴同轴;
横向力矩,力矩轴线与轴线一致,与回转减速器旋转轴同轴;
轴向力、横向力和横向力可合并为风合力。
三.光伏板风载荷仿真建模
根据跟踪式光伏发电设备的几何参数,建立了几何模型和流体域,本文模型为两个长8.0m×1.9m×0.04m的平板,确定流体域的尺寸为:70 m×55 m×25 m,模型中心距地面高度为 4.2 m,风的入口面距模型中心距离为 20 m;对仿真模型划分了合适的网格,在流速变化大的位置网格划分更密,提高计算精度;根据实际的流体风环境,设置选用标准的湍流模型,流体域材料为空气,设定法向入口风速为14m/s,气温20℃且绝热,参考气压为1标准大气压,流体视为不可压缩流体;根据仿真模型的特点,选择流固耦合求解器;最后通过后处理计算,得到了各种姿态角的风力和风力矩。
四.各种姿态角光伏板的风载荷分析
因为光伏板始终跟踪太阳旋转,所以其迎风角一直在变化。通过仿真后处理,计算得到各种姿态角度光伏板的风载荷。本节对风载荷随姿态角的变化规律、最大值和特定角度产生最大值的原因进行了研究。
根据各种姿态角度光伏板的仿真风力和风力矩,研究得到风载荷的影响因素和变化趋势;根据流体仿真,研究特定姿态角产生最大风载荷的原因。主要得出一下结论:
(1)各向风力主要与力方向的迎风投影面积有关,风力的形成原因是光伏板表面的压差阻力,光伏板迎风面阻碍流体通过形成正风压,背风面尾流区形成负风压;
(2)各向风力矩主要与迎风面积和特定角度的偏心风载力有关,风力矩的形成原因是光伏板表面风压不均产生的偏心风力和边缘涡旋吸力;
(3)在回转角0°、俯仰角90°时,迎风面积最大,风合力最大,最大值为5572N,该值是光伏板最大风载力;
(4)在回转角0°、俯仰角30°时,光伏板不均布的风压力,产生y轴方向的力矩,俯仰力矩最大,最大值为1649.2N·m,该值是俯仰减速器风载扭矩;
(5)在回转角60°、俯仰角90°时,光伏板不均布的风压力,产生z轴方向的力矩,横向力矩最大,最大值为5084.4N·m,该值是回转减速器风载扭矩。
五.光伏板风载荷仿真计算的实验验证
通过实验测量风载荷,对风载荷仿真计算结果进行验证。本文在自然低风速环境下进行试验:首先,采集实验现场低风速环境参数,进行风载荷仿真;然后,实验测量跟日减速器的负载扭矩;最后,对比仿真风力矩和实测风力矩的相关性,验证低风速风载荷仿真正确性和流固耦合仿真方法的可行性。
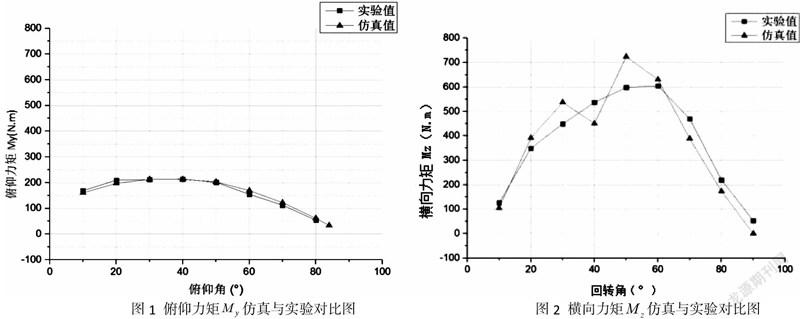
1.对比俯仰力矩的仿真值和实测值
如图1通过分析数据:实验值的平均值为165.7N·m,最小值为53.8N·m,最大值为214.1N·m;仿真值的平均值为167.3N·m,最小值为33.5N·m,最大值为213N·m;仿真值与实测值的皮尔森相关系数为0.87,呈高度線性相关[2]。
2.对比横向力矩的仿真值和实测值
如图2通过分析表中数据:实验值的平均值为378.5N·m,最小值为53.2N·m,最大值为604.7N·m;仿真值的平均值为377.9N·m,最小值为0.4N·m,最大值为724.4N·m;仿真值与实测值的皮尔森相关系数为0.85,呈高度线性相关[2]。
六.结论
本文研究了光伏板的风载荷构成、风载荷理论计算方法和风流动特性,为分析风载荷提供理论基础。建立了风载荷模型,使用流固耦合仿真方法,对不同姿态角度的跟踪式光伏发电设备进行了风载荷仿真分析。通过分析仿真数据,研究了风载荷随姿态角变化的规律。通过流场及风压仿真图,分析了特定角度产生最大风载荷的原因。在现有设备上,安装了一套风力矩测量实验系统,对比分析风力矩的实测值和仿真值,验证了仿真方法的可信性。
本研究通过使用COMSOL Multiphysics软件的流固耦合模块,仿真得到了光伏板风载荷,模拟了实际风压的分布特性,通过实验基本证实了该仿真建模方法的可信性和可行性。本文的风载荷仿真方法对光伏设备的研发设计有工程指导意义。
参考文献
[1]李在贵.天线结构设计[M].第一版.高等教育出版社,1986.
[2]杨帆,冯翔,阮羚等.基于皮尔逊相关系数法的水树枝与超低频介损的相关性研究[J].高压电器,2014,50(06):21-25+31.
1.沈阳佳晔能源科技股份有限公司 辽宁沈阳 110000;
2.沈阳飞亚水艺园景工程有限公司 辽宁沈阳 110000
