煤矿用无人驾驶辅助运输车辆的蒙特卡罗定位方法

鲍 文 亮

(中国煤炭科工集团太原研究院有限公司，山西 太原 030006)

0 引 言

无轨胶轮车在国内外煤矿的辅助运输系统中得到了广泛应用[1-3]。然而由于人员密集度高和劳动强度大的特点，无轨胶轮车辅助运输仍是煤矿生产中安全隐患突出的环节[4-5]。实现这类辅助运输车辆无人驾驶是煤矿安全生产的现实需求，也是智慧化矿山建设的必然趋势[6]。当前关于煤矿用辅助运输车辆无人驾驶技术的研究仍处于起步阶段，相关文献较少。

车辆自主定位是无人驾驶技术体系中的重要一环。定位技术用于建立车辆与环境地图之间的相互关系，也被称为位置估计。在移动机器人领域，概率技术因其鲁棒性好和模型依赖程度低等优点已成为研究热点和发展趋势[7-8]。移动机器人(涵盖无人驾驶车辆)的概率定位方法基本都源于贝叶斯滤波。得到广泛应用的扩展卡尔曼滤波(EKF)定位和无迹卡尔曼滤波(UKF)定位将机器人位姿的置信度表示为一个参数化的高斯分布[9]。其主要局限是不能解决全局定位和绑架问题，此外需要从传感器测量提取特征进行处理。DELLAERT等[10]提出了基于粒子滤波的定位方法，并将这一方法命名为术语蒙特卡罗定位(Monte Carlo Localization，MCL)。粒子滤波通过状态采样表示置信度，是贝叶斯滤波的一种非参数实现形式[11]。MCL易于实现并且适用范围广，受到了广泛关注。大量的研究工作针对算法中出现的粒子缺乏问题[12-13]，粒子退化和建议分布机制缺陷问题[14-16]，以及粒子集规模自适应调整优化等方面展开[17-18]。

笔者以煤矿用辅助运输车辆的自主精确定位问题为研究对象，在场景及需求分析的基础上，讨论了激光测距扫描的适用性，提出了将巷道内车辆的精确定位维持在一个典型场景所对应的区域地图范围内进行的策略；基于车辆的速度运动模型和激光测距的似然域模型，论述了蒙特卡罗定位方法的实现，提出了调节似然域模型不确定性范围，从而避免定位算法失败的方法，仿真结果验证了该方法有效,实现了车辆在煤矿井下巷道的自主定位。

1 场景分析

煤矿用车辆自主行驶时，在巷道延伸的纵向方向和垂直于巷道壁的侧向方向存在不同的定位要求。纵向方向上，在一个重要地点所对应的有限区域范围内，车辆需要获取精确位置坐标；而在一段仅作为通道存在的狭长直巷内则无需该信息，即需要时精确定位。侧向的情况则不同，为确保在规定的狭窄车道内安全行驶，车辆需要时刻了解自身相对巷道中心线基准的位置和转向姿态角，即实时精确定位。

尽管基于特征测量的定位方法能够实时获得车辆的全部三自由度位姿估计，但在井下巷道环境应用时存在一定的局限。考虑对重要地标进行观测的情况，由于狭窄巷道空间走向的单一性，地标只能依线性排列设置，从而长距离测量将不可避免。此时，特征方位角的测量噪声将对车辆侧向定位精度产生较大制约。并且由于侧向连续实时定位的要求，在车辆一次观测的可及范围内至少需要设置1个地标，这在煤矿长距离巷道环境下工程实现代价较大。

综合上述定位需求，侧向的激光测距扫描为车辆自主定位提供了一个可供选择的合理解决方案。测距扫描提供原始测量数据，而不是特征测量。此时侧向位置和姿态角能够获得实时的测量更新；对于纵向位置，当车辆未到达重要区域而不需要精确定位时，可以维持在一个多假设状态。

煤矿井下车辆行驶的巷道环境的一个典型场景如图1所示，图中同时绘出了车辆侧向测距扫描的情形，其中，A、B、C、D为图中4个固定点，x′和y′为车体坐标系的2个坐标轴，θ为车辆局部坐标系相对于全局坐标系的转角，逆时针旋转为正。在一段狭长直巷的中间某个位置发生巷道的交汇连接，该位置处出现的可能是硐室、联络巷或交叉巷。通常对于车辆来说这里对应一个重要地点或场所，车辆行驶的全域环境基本可认为是一定数量的该典型场景的集合。

图1 矿用车辆行驶的巷道环境的一个典型场景Fig.1 Typical scene of laneways in which vehicle for coal mine operates

基于分层定位技术，提出将车辆精确定位问题维持在一个典型场景所对应的区域地图范围内进行的策略，并进一步详细讨论蒙特卡罗定位方法的实现。需要强调说明的是，任何一个典型场景内只包含1处巷道交汇。这样划分的意义在于，在某一场景内的全局定位问题下，当传感器未观测到巷道交汇处时，位姿置信度可能呈现1个多峰分布，在纵向方向维持多个位置假设；而当传感器一旦观测到巷道交汇地点时，置信度迅速收敛到1个单峰分布，车辆将确信自己获得了正确的位置估计。如果1个典型场景中包含多处巷道交汇，通常在观测到2个以上巷道交汇地点前置信度将保持多峰分布，即维持多假设的情况，车辆有可能因此错过在某个重要地点获得正确位置估计的时机，即未能实现“需要时精确定位”，从而影响正常行驶。

2 蒙特卡罗定位算法

定义全局坐标系如图1所示，其中x轴沿巷道中心线定义，y轴在巷道横截面内方向垂直于巷道壁。车辆在全局坐标系下的位姿状态变量为

(1)

式中，(x,y)为车辆局部坐标系原点在全局坐标系下的坐标值。

在概率体系下，k时刻车辆的位姿由置信度bel(ξk)描述，其定义为后验概率分布p(ξk|ο1:k,u1:k)。

bel(ξk)≐p(ξk|ο1:k,u1:k)

(2)

式中，ο1:k和u1:k分别为k时刻以前所有的测量值和控制量。

当车辆首次进入某个典型场景时，首先面对的是在这个区域地图范围内的全局定位问题，同时考虑到车辆侧向的激光测距扫描提供的是原始测量值而非特征测量，从而EKF或UKF定位方法不适用于这一定位问题的解决。MCL通过一个状态采样获得的粒子集描述置信度bel(ξk)，能够解决位置跟踪、全局定位以及绑架问题，并且可以处理传感器的原始测量值而无需提取特征，算法按照如下步骤实现：

1)给定k-1时刻的粒子集χk-1，当前k时刻的uk、οk，以及环境地图m。

2)对所有j=1，2，…，N(N为粒子数量)进行采样。

(3)

(4)

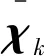
算法的第3步根据每一个预测状态的权值大小进行重要性采样，实现了贝叶斯滤波的测量更新过程。得到的粒子集χk能够描述任意形状(如多峰分布)的置信度bel(ξk)分布。如果为简单地获取定位估计，可采用高斯近似进行密度提取。分别以样本均值和样本方差作为近似高斯分布的一阶矩和二阶矩参数，得到定位估计。

3 运动与测量模型

3.1 运动模型

矿用辅助运输车辆一般采用阿克曼转向或铰接转向的驱动结构，其中前者用于运人车等轻型胶轮车，后者用于支架搬运车等重型车。这2类结构都具有非完整运动学约束[19]，具体来说，它们都具有1个瞬时旋转中心，控制自由度都等于2，由1个差分自由度和1个可操控自由度组成。对于阿克曼转向结构，可选取车辆纵向速度v和旋转角速度ω作为名义控制输入。而对于铰接转向结构车辆，其前后车体满足一个与铰接角相关的运动学约束关系，可选取前车体的纵向速度v及其旋转角速度ω作为名义控制输入。由此，采用统一的速度运动概率模型的采样算法完成式(3)表示的采样过程[20]。首先，向名义控制中加入控制噪声采样。

(5)

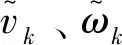
(6)

式中，Δt为采样间隔。

3.2 测量模型

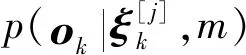
(7)

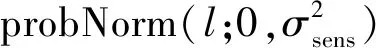
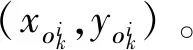
(8)

(9)

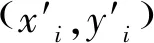
这里将激光测距返回的最大距离读数视为测量失败，将其简单丢弃。则式(7)—式(9)给出了激光测距扫描的似然域测量模型，由此可根据式(4)进行定位算法中权值的计算。

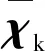
为适应MCL，笔者提出不确定性范围可调的似然域模型修正方法，即将式(7)修正为

(10)

其中，σLHF为可调节参数。增大似然域不确定性σLHF使得在正确状态附近范围内的预测状态值能够获得更高的测量概率(权值)，这时重要性采样能够基于测量信息采样出更接近真实值的状态。

4 仿真验证及分析

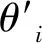
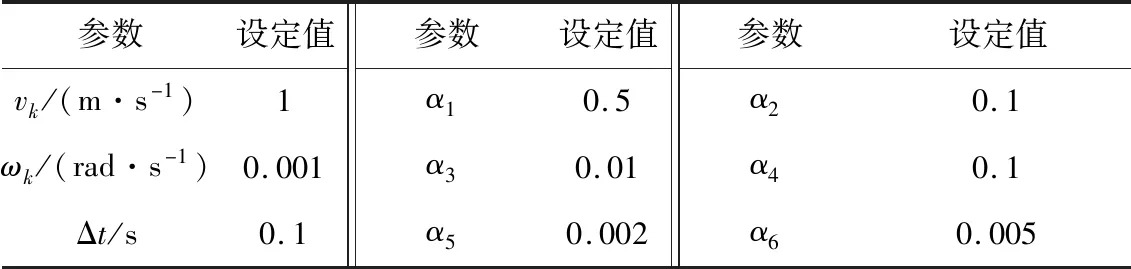
表1 仿真用运动参数Table 1 Motion model parameters used in simulation

MCL方法首先要解决全局定位问题。选取粒子数N=30 000，在地图范围内，按照均匀分布在车辆位姿状态空间进行采样，获得初始时刻粒子集，粒子在x-y平面的分布情况如图2所示。

图2 初始时刻的粒子在x-y平面的分布情况Fig.2 The distribution of particles in the x-y plane at the initial monment

MCL仿真过程中，调节模型参数σLHF=1 m，获得了良好的估计效果。进行参数调节时，当σLHF取值较小(向σsens靠近)，则粒子基本不能收敛到真实位姿附近，与分析情况相符。仿真得到MCL过程中不同时刻的粒子在x-y平面的分布情况如图3所示。设车辆的各位姿状态是条件独立的，通过高斯近似对粒子集进行密度提取，并以高斯分布的均值作为车辆位姿估计，则车辆位置估计的情况如图4所示，车辆姿态角估计如图5所示。

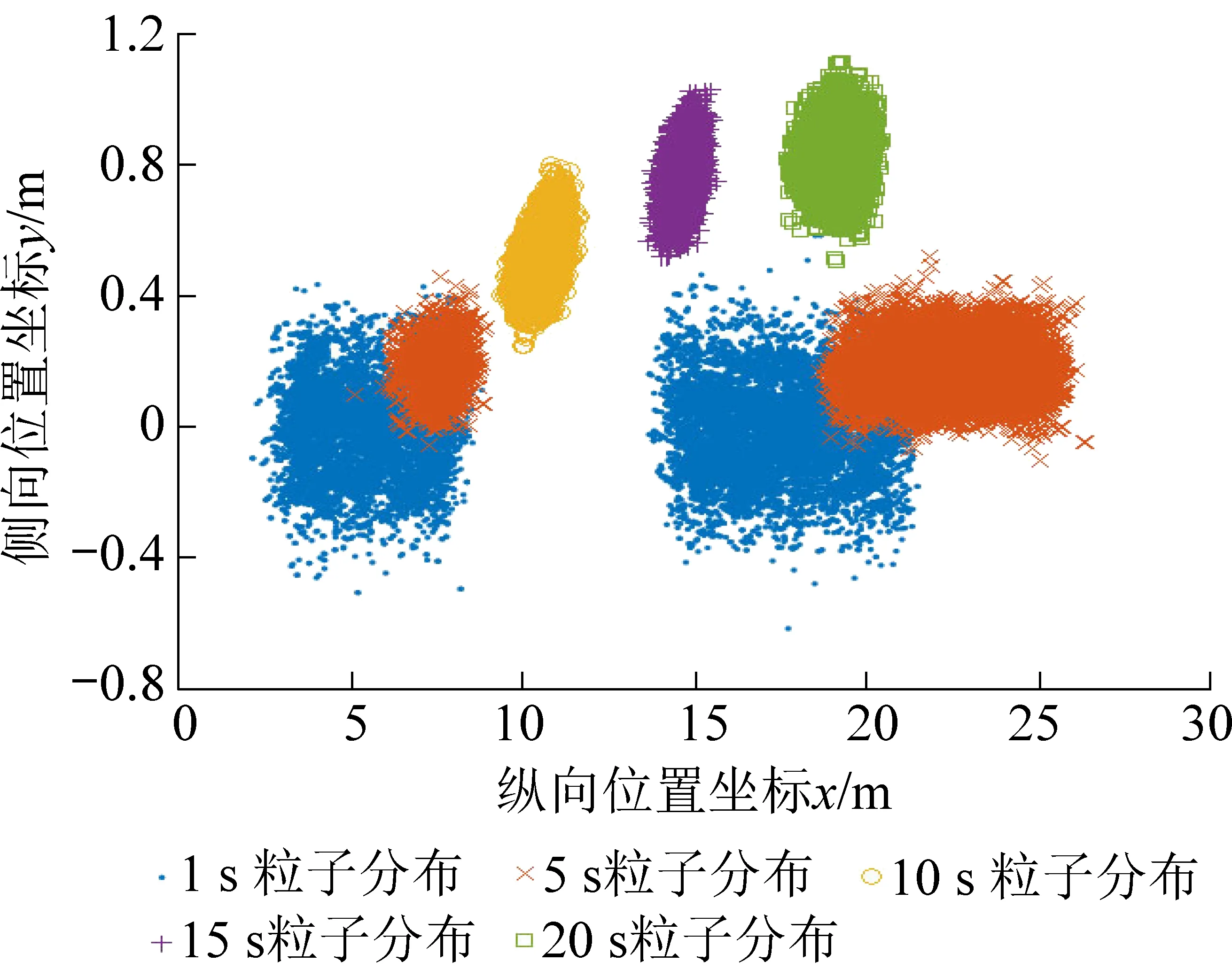
图3 不同时刻的粒子在x-y平面的分布情况Fig.3 The distribution of particles in the x-y plane at different monments

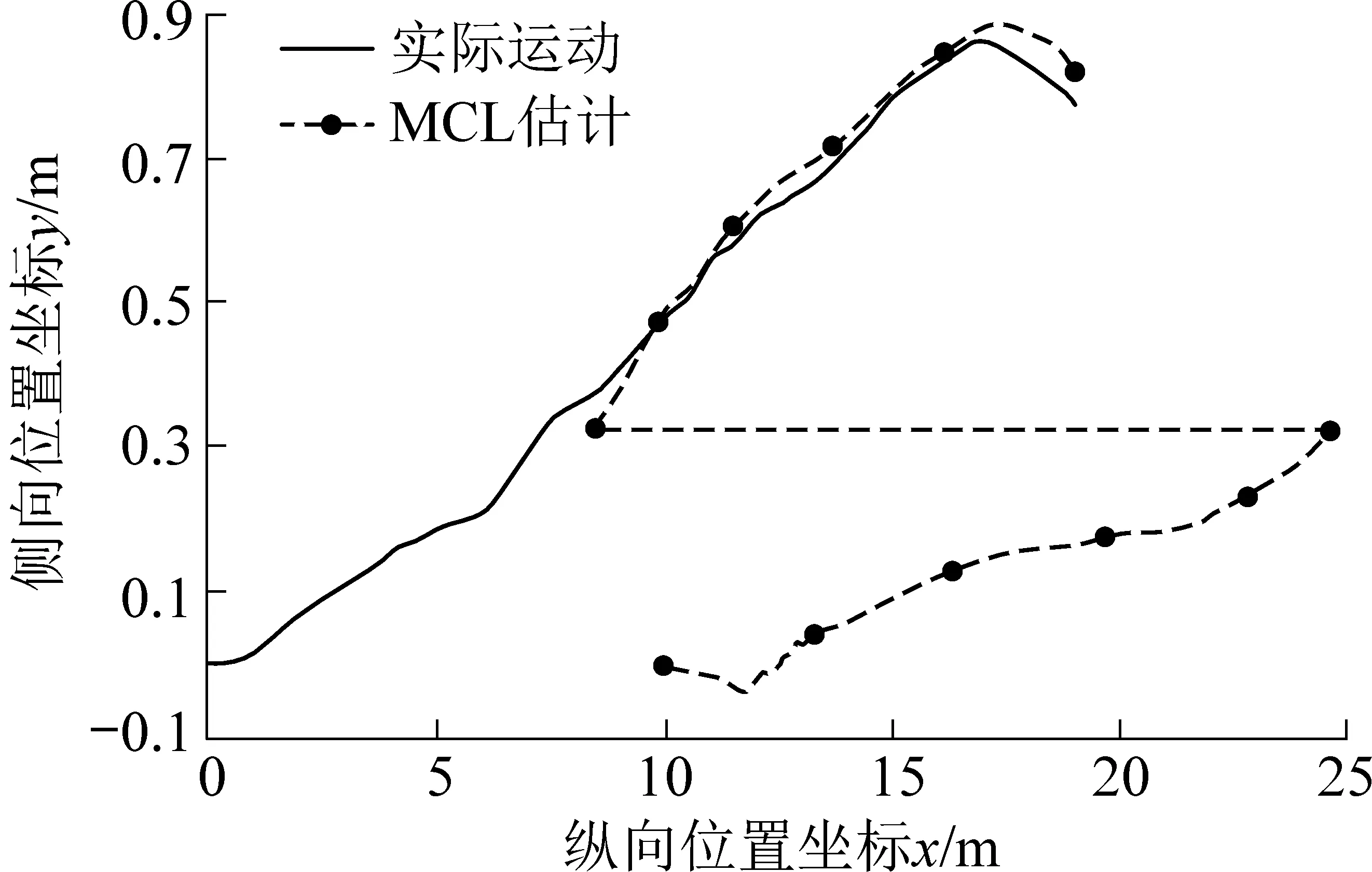
图4 MCL的车辆位置估计Fig.4 Position estimation of vehicle by MCL

由图3可得，在MCL开始后的一段时间里，初始时刻均匀分布的粒子聚集在2个区域之内。此时状态置信度对应1个多峰分布，即存在多个可能的位姿假设，这一阶段反映了车辆的全局定位过程。随着MCL的进行，粒子聚集到了一个确定的区域附近，该阶段反映出车辆已进入位置跟踪过程。图4的位置估计曲线也清晰地表现出这一过程变化。当置信度具有多峰分布时，高斯近似密度不能有效拟合真实置信度分布，从而使得位置估计具有较大偏差。当置信度变为单峰分布时，高斯近似精度大幅提升，位置估计迅速逼近实际运动轨迹。事实上，结合图4和图5可以看出，在整个MCL过程中，侧向位置估计和姿态角估计都很好地反映了实际状态值，真正导致置信度多峰分布的因素是纵向位置的后验分布特性。在t≈8 s时，置信度由多峰分布收敛为单峰分布，该过程反映了车辆侧向的激光测距扫描观测到地图中的巷道交汇这一事实。综上可知，车辆的定位特性确实满足了侧向“实时精确定位”和纵向“需要时精确定位”的要求。

为对比定位性能和效果，基于相同的实际运行轨迹，对EKF定位的实现情况进行了仿真。首先，EKF定位不能解决全局定位问题，因此仿真使用了车辆真实初始位姿附近的一个窄高斯分布作为初始值进行位置跟踪。其次，EKF不能直接处理前述的车辆侧向激光测距扫描的测量信息，仿真采用基于地标特征测量的方法实现EKF定位。考虑到煤矿巷道实际环境特点，假设可同时观测的地标数量为1个，地标在地图中的设置坐标为(100,0)，单位m。最后，分别设置特征方位角的测量误差σ为0.05和0.10 rad，仿真得到EKF定位的车辆位置估计情况如图6所示。基于MCL以及2种条件下的EKF定位仿真结果，绘制各自的侧向位置估计误差曲线，如图7所示。

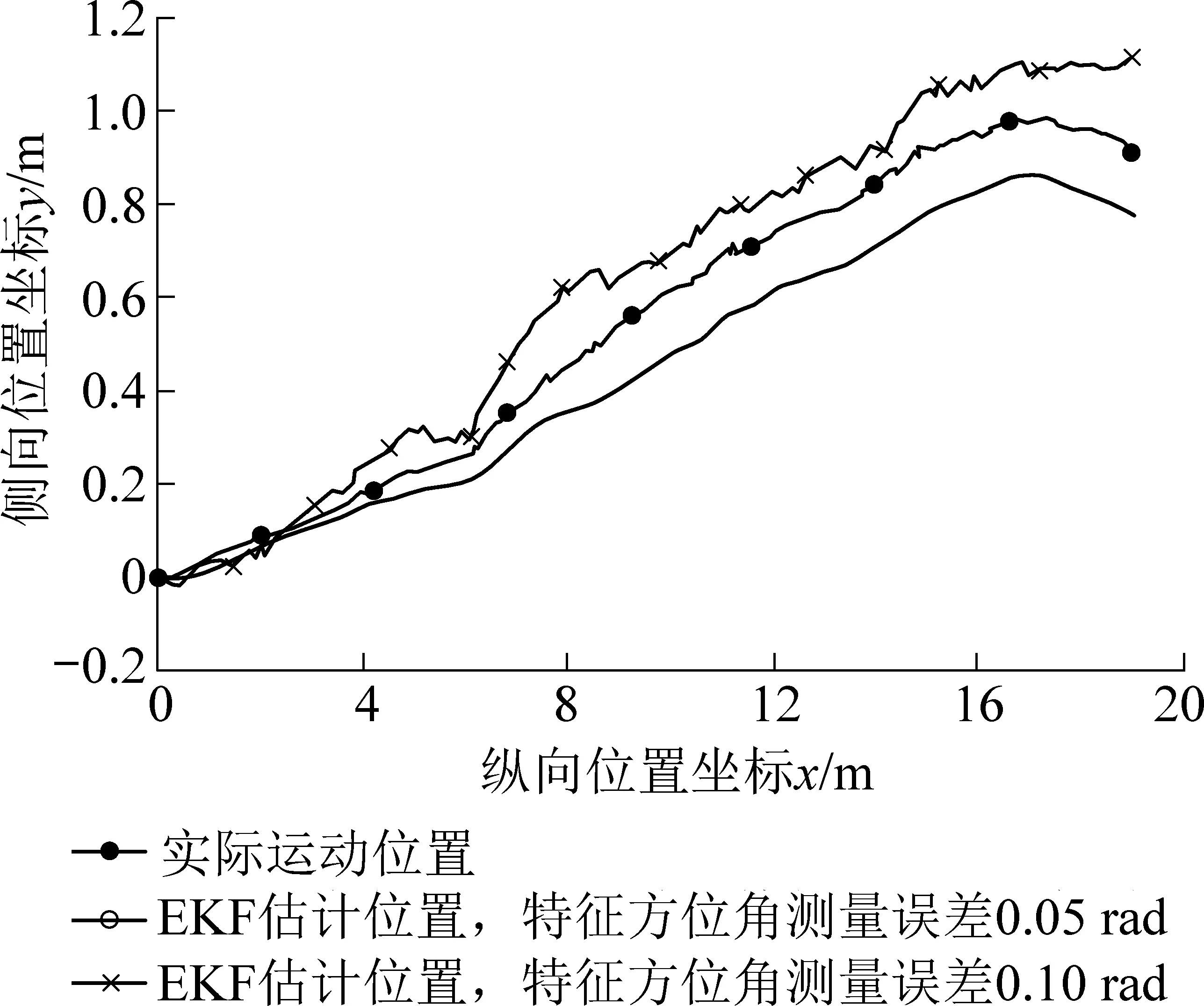
图6 EKF的车辆位置估计Fig.6 Position estimation of vehicle by EKF

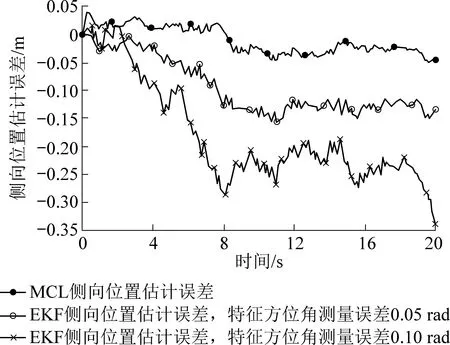
图7 侧向位置估计误差对比Fig.7 Comparison of errors of lateral position estimation

计算MCL和2种条件下EKF定位的侧向估计误差统计值，见表2。

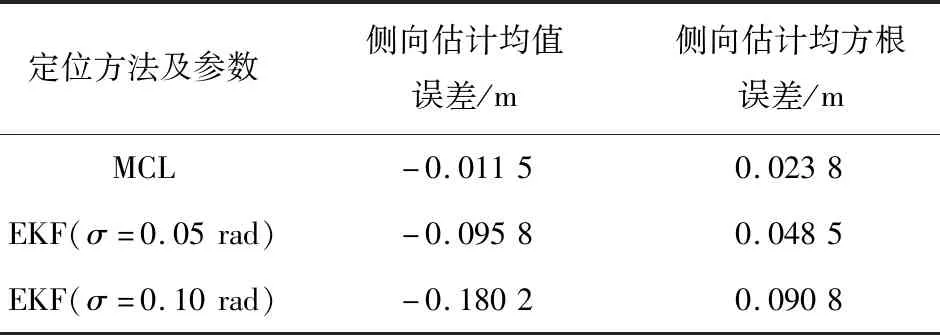
表2 侧向位置估计误差对比Table 2 Comparison of errors of lateral position estimation

可以看出，在基于特征测量的EKF位置跟踪定位情况下，侧向的定位精度受特征方位角测量误差的影响较为显著。对于煤矿巷道环境长距离单特征测量，适宜的特征测量方法和高精度传感器成为现实制约。

5 结 论

1)通过定义煤矿巷道环境的典型场景，矿井全域地图可分解为若干典型场景区域地图，矿用车辆的定位问题在区域地图范围内得到解决，简化了车辆全局定位的复杂度和运算量。

2)在巷道环境中，纵向和侧向相关位姿状态估计的及时性要求不同，采用车辆速度运动模型及激光测距传感器似然域模型的蒙特卡罗定位算法能够很好地适应这一要求，解决了全局定位和位置跟踪问题。

3)为适应蒙特卡罗定位算法的特点，将似然域模型中的不确定性参数作为可调节量，当传感器噪声水平较低时，适当增大该量值能够保证算法成功运行。

4)相比巷道环境下的扩展卡尔曼滤波定位，除能够解决全局定位问题外，蒙特卡罗定位方法使侧向位置估计精度得到有效保证。