基于烟气扩散特征的林区隧道火灾人群疏散模型

2021-11-30王羽尘马健霄刘宇航白莹佳

南京林业大学学报（自然科学版） 2021年6期

王羽尘，马健霄，刘宇航，白莹佳

(南京林业大学汽车与交通工程学院，江苏南京 210037)

随着全球气候变暖，极端天气事件增加，森林火灾发生频率逐年上升，快速、高效地扑灭森林火灾成为亟待解决的问题[1-2]。林区隧道作为一种在林区地下建造的工程建筑物，相对于林区道路，其空间封闭，除了入口和出口外，不会造成大量森林砍伐[3-4]。同时，作为连接林区与外界的运输通道，其承担着通勤、运送扑火人员和物资的作用，保障林区居民日常出行和生活。目前，关于林区隧道的研究大多针对洞口照明[5]、隧道内排水[6]和隧道设计[3]，对隧道火灾人群疏散研究较少。而林区隧道本身具有纵向狭长、内部封闭、通风受限的空间特点。当发生火灾后，烟气的快速扩散缩小了行人的可视范围，降低其对距离的感知，对身处其中的疏散人群产生影响，导致联络与逃生困难，如果不及时控制，蔓延至林区，将造成不可扭转的损失。因此，研究林区隧道烟气环境中人群的疏散规律，确定对应的保障措施，对于提高疏散效率、减少人员伤亡和保障林区的安全具有重要意义[7]。

基于上述分析，目前在描述林区隧道烟气环境中行人的移动规则时，未同时考虑烟气环境对疏散人群能见度和烟气动态变化对疏散行为的影响，难以体现林区隧道烟气环境中人群的疏散规律。针对上述问题，本研究在分析烟气扩散特征基础上，采用元胞自动机[21]中的地板场(floor field, FF)模型框架并进行拓展，建立烟气扩散模型来描述烟气的动态变化，分别引入消光系数和烟气场强来描述烟气对距离感知及行人在烟气中的逃生行为的影响，提出了基于烟气扩散特征的改进模型，并应用于林区隧道烟气环境模拟仿真，以期为林区隧道内发光标志等安全设施的设置提供依据。

1 基本模型

1.1 模型选用

国内外学者从宏观和微观的角度提出了许多人群疏散模型，其中微观模型主要研究个体间相互影响导致的群体动态现象，具有相对较大的计算量，描述更加多样化。典型的微观模型主要有元胞自动机模型、社会力模型和排队论模型等。其中，元胞自动机能较好地反映行人的各项特征，在空间、时间上具有离散状态，是描述复杂演化现象的一种简化模型，广泛应用于描述二维平面内行人流疏散问题[22-23]。

利用元胞自动机模型描述疏散过程时，对群体之间、群体和障碍物之间的力效应的处理方式，主要有以下3种。

1)直接忽略这种力效应，此模型为传统的元胞自动机模型。

2)结合社会力模型中个体的自驱力、群体间的排斥力、障碍物排斥力的计算公式，直接应用于元胞自动机模型，并将力效应处理为确定性作用力，此模型为格子气模型。

3)考虑排斥、吸引及其他力效应对行人运动的影响，将力效应分别处理为静态场强和动态场强。通过复杂的运动规则和选择机制，间接地体现疏散人群的受力情况，人群接触产生的相互作用力可通过元胞进行传递，此模型为地板场(FF)模型。FF模型能够间接描述力的作用，能较好解释疏散拥挤产生的力效应。本研究拟采用此模型进行研究。

1.2 基本FF模型

在FF模型中，行人向邻域转移的概率受到静态和动态场强的影响，静态场强(Sij)描述了元胞到出口的距离，该值取决于房间的几何形状。而动态场强(Dij)通过参考其他行人走过的线路信息，描述行人间的从众行为。动态场强具有时间依赖性，并根据扩散和衰减规律进行修正。惯性场强(Iij)是行人当前运动方向对后续移动偏好的影响。

在每个时间步长中，疏散者判断移动区域内各个元胞的场强大小，并考虑其余元胞是否被行人和障碍物所占据，得到移动区域内行人向其他元胞的转移概率(Pij)。

Pij=Nexp(kDDij)exp(-kSSij)Iij(1-ηij)εij。

(1)

在该模型中，为了描述疏散人群的运动，采用了Von Neumann元胞自动机邻居类型，如图1所示。

图1 Von Neumann邻居类型Fig.1 Neighbor cells for the Von Neumann

2 基于烟气扩散特征的改进模型

2.1 烟气扩散及其影响

2.1.1 烟气扩散模型

烟气扩散的确定性理论是将建筑物分为上热烟气层和下冷空气层，伴随隧道火灾的发生，高温烟气在浮力驱动下流向顶端，当碰到隧道顶棚后向四周散开，形成上部热烟气层[24]。本研究在量化烟气扩散时，为了减少模型计算的复杂性，增加模型的可理解性，将烟气扩散规律描述为数学模型。假定林区隧道内的火灾由局部点引发，烟气在浮力的作用下流向隧道顶棚，进而产生高温烟气，并在一定范围内以一定的扩散频率hs向周围扩散，则扩散范围Rs是关于扩散频率hs的函数，如式(2)所示。

Rs=f(hs)。

(2)

式中：Rs为烟气扩散的范围，元胞；hs为烟气扩散的频率，元胞/s。

2.1.2 烟气扩散的影响

1)对距离感知的影响。可见光的波长λ为0.4～0.7 μm，一般火灾烟气中烟的颗粒直径d为几微米到几十微米不等，即d>2λ。在疏散过程中，火灾燃烧产生的烟粒子会遮蔽可见光，对人群视物以及距离感知产生不利影响。在相同反光或照明的情况下，影响遮蔽程度的关键因素是消光系数，即不同燃烧物产生的烟气混合物和空气的衰减系数[25]。

随着烟气扩散，隧道将被分为可见区域和烟气蔓延区域。在可见区域中，行人可以看到并准确感知出口，保持正常的疏散运动；在烟气蔓延区域，行人的移动受到消光系数的影响，对距离感知产生误差。随着烟气扩散范围的变大，可见区域逐渐变为烟气蔓延区域，具体情况如图2所示。

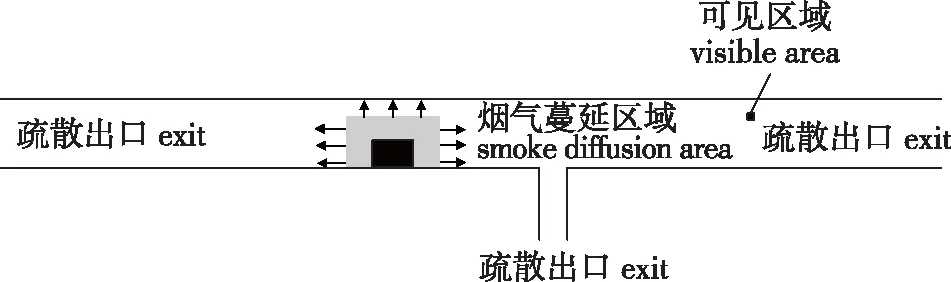
图2 可见区域和烟气蔓延区域图Fig.2 The visible and smoke diffusion regions

2)对逃生行为的影响。烟气扩散将直接影响行人的心理状态，疏散人群需要一定决心做出穿越烟气的逃生行为，否则将会留在原地或反向转移到更合适的逃生通道[26]。同时，身处烟气中的行人易丧失主观判断，产生恐慌心理，下意识反向逃离，容易造成迂回、反向转移的逃生行为。

2.2 更新规则描述

模型的更新规则采用并行更新的方式，具体的更新规则描述如下。

2.2.1 计算静态场强

行人受火灾燃烧物的影响，移动受到限制，无法直接穿越火灾区域。烟气扩散对行人的距离感知产生影响，导致行人迂回移动。本研究将火灾燃烧物所在区域的静态场强设置为无穷大来表示不可穿越，用消光系数(αij)来描述烟气扩散对距离感知的影响。综上所述，基于Dijkstra算法[27]计算各个元胞与所有出口之间的最小距离，如式(3)所示。

(3)

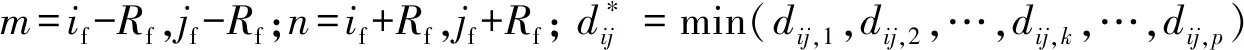
由于Von Neumann元胞自动机邻居类型仅有上、下、左、右4个方向，若出口k所在位置元胞为(i0,j0)，则元胞(i,j)到该出口k的距离dij,k=|i-i0|+|j-j0|。(if,jf)为火灾所在的元胞，(if,jf)到该出口k的距离dijf,k=|if-i0|+|jf-j0|。

根据式(3)和dij,k绘制隧道内有无火灾燃烧物和烟气时的静态场强分别如图3所示。其中，红色区域表示对静态场强值较大的位置，黑色区域为火灾燃烧物所在位置，行人不可通过。

图3 无火灾及有火灾燃烧物和烟气时的静态场强Fig.3 Field strength without fire and with fire combustion and smoke

在没有动态场的干扰下，人会倾向于从静态场强较大的位置移动至较小的位置。从图3可知，火灾燃烧物和烟气的存在会增大周围元胞的静态场强，导致行人面对火灾燃烧物和烟气会产生逃离、迂回的行为。

2.2.2 计算动态场强

动态场强主要考虑以下3步进行计算：

1)每当有一个人经过时动态场强加1，即Dij=Dij+1。

2)考虑到每个元胞动态场强的消退和扩散，即

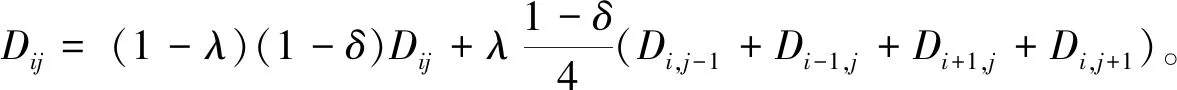
(4)

式中：Dij表示动态场强，λ表示动态场强向外扩散的概率，δ表示消退概率，Di,j-1，Di-1,j，Di+1,j，Di,j+1分别表示元胞(i，j-1)，(i-1，j)，(i+1，j)，(i，j+1)的动态场强。

3)将动态场强无量纲化，即

(5)

2.2.3 计算烟气场强

当行人位于烟气的影响范围Rs内，离烟气产生中心越近，受到的排斥作用越大；当行人位于Rs外，则不受烟气的影响。使用元胞(i,j)及其到烟气边缘的距离来反映烟气场强(Fij)，如式(6)所示。

(6)

式中：dij表示元胞(i,j)到烟气边缘的距离。

2.2.4 计算转移概率

每个目标元胞的转移概率Pij如式(7)所示。

Pij=Nexp(kDDij)exp(-kSSij)exp(-kFFij)Iij(1-ηij)εij。

(7)

2.2.5 冲突处理

由于模型的并行更新规律，存在两个或多个行人可能会选择相同的目标元胞。引入静止概率μ来定量描述该情况以及堵塞现象的形成。当其中1人以概率1-μ向目标元胞运动，其余人以概率μ静止，参与冲突的行人均有相同的概率成为实际移动的人[28-29]。

2.2.6 持续移动

疏散人群按照每个目标元胞的转移概率运动，直至到达疏散出口。

2.3 疏散模拟流程

模拟流程分为3个模块：场景模拟、行人的移动模拟和烟气扩散模拟。根据隧道数据建立场景模型，包括平面几何尺寸，出口宽度和位置，行人疏散通道和疏散方向等。行人移动模拟包括计算每个元胞的静态场强Sij、动态场强Dij、烟气场强Fij和惯性场强Iij，设置不同场强的敏感性参数kD、kS、kF，最终得到每个目标元胞的转移概率Pij。

模拟过程中，行人按照静态场强、动态场强和烟气场强，随机差异化地向疏散通道或隧道出口进行移动。发生冲突时，按照冲突准则进行处理。烟气扩散模拟相对较为简便，可根据具体情况确定火灾燃烧物位置、消光系数αij、烟气扩散范围Rs和扩散频率hs。本研究选取隧道内剩余人数的实时变化曲线作为疏散效率的评价指标。基于上述设定，考虑烟气扩散的林区隧道人群疏散模型应遵循以下流程，如图4所示。

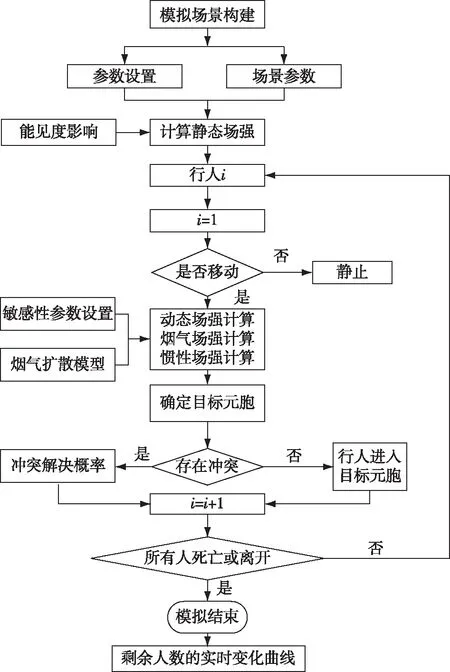
图4 疏散模拟流程图Fig.4 Simulation of evacuation

3 仿真与参数影响分析

3.1 仿真环境

使用python 3.7.0及其中的numpy1.20.1，random和csv程序库搭建基于烟气扩散特征的人群疏散仿真模型，以神农架林区209国道万福隧道的某段隧道作为试验场景(图5)。隧道行车道宽3×3.75 m，左侧路缘带宽0.75 m，右侧路缘带宽1 m。假定人行横通道距隧道入口235 m，距隧道出口285 m，通道宽2 m，长30 m。系统是以元胞为单位的平面坐标系，每个格点1 m×1 m，疏散空间的尺寸为520 m×13 m，在隧道的中部有10 m×5 m的火灾，疏散边界的厚度为3个元胞，隧道两侧各有疏散出口。

图5 可见区域和烟气蔓延区域图Fig.5 The visible and smoke diffusion region

3.2 基本参数和假定

模型的参数主要基于已有研究[30-31]确定，初始人群密度D1=0.05人/m，疏散空间中共有338人，行人移动速度为1.5 m/s。场强模型的基本参数及其取值为：烟气扩散的极限范围Re，取值100(元胞)；火灾燃烧物范围Rf，取值4(元胞)；静止概率μ，取值0.1；扩散频率λ，取值0.2；消退概率δ，取值0.2；动态场强敏感性参数kD，取值0.2；静态场强敏感性参数kS，取值0.5；烟气场强敏感性参数kF，取值0.3；惯性场强Iij，取值1.15。

3.3 疏散过程

设定t为当前模拟时间步长。当t分别取1、50、100、200、400 s时，行人在烟气扩散环境下的疏散过程如图6所示。

图6 不同时间的疏散情形Fig.6 Evacuation situations at different times

3.4 参数分析

疏散过程中行人在林区隧道烟气环境中的场强和转移概率受到消光系数和扩散频率影响。分别研究消光系数和扩散频率对行人移动过程、剩余人数和平均疏散时间的影响。同时，为提高仿真精度，每项统计结果均采取30次模拟结果的平均值。

3.4.1 消光系数的影响

本组参数分析取消光系数αij={1.15,1.25,1.35}，不考虑扩散频率hs的影响。不同αij对应的系统内剩余人数随时间的变化如图7所示。基本模型的平均疏散步长为508 s，αij为1.15、1.25、1.35时的平均疏散步长分别为514、557、579 s。

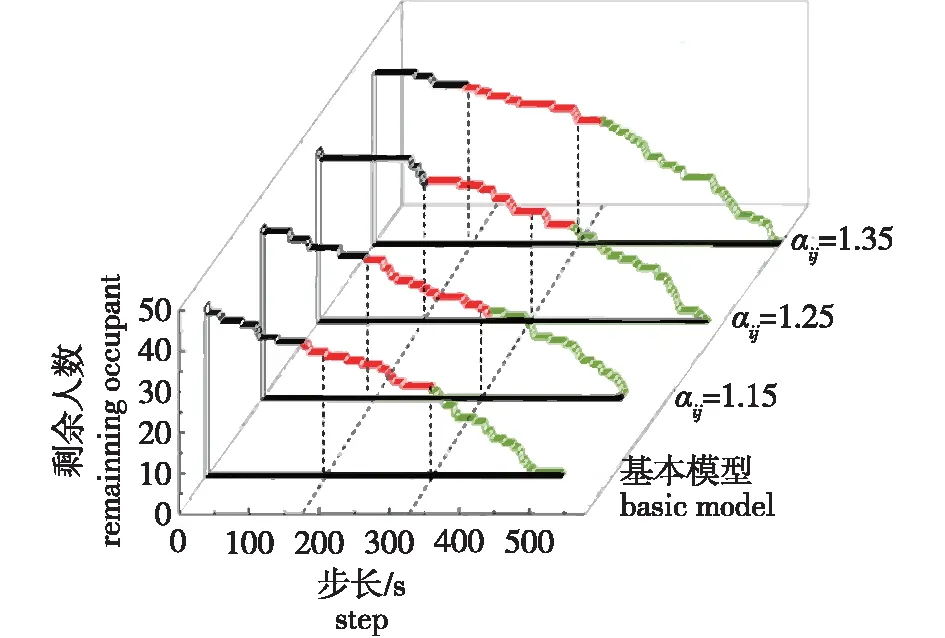
图7 不同消光系数值对应的剩余人数变化曲线Fig.7 Variation curves of remaining occupants related to different αij values

从图7中可知，当模拟步长小于170 s时，成功疏散的行人初始分布在距离疏散出口较近的位置，存在剩余人数在一段时间内保持不变的现象。这是由于行人所处空间为纵向狭长的隧道，需要一段时间才能到达出口。当步长为170～330 s，成功疏散的行人距离隧道出口较远，处于长时间运动中，受到消光系数影响较明显，且系数越大，单位时间内成功疏散到出口的人数越少。当步长大于330 s，行人位于起火点附近，受到烟气影响较大，到达出口的时间较长，出现剩余人数持续降低的现象。

引入消光系数，行人的平均疏散步长出现明显增加。相比基本模型，行人的平均疏散步长增加了71 s，并且数值越大，疏散时间越长。在模拟实例的物理环境中，引入消光系数能够体现疏散过程中行人因距离的聚集和移动缓慢现象。同时，不同时间步长内空间形态、烟气影响和距离三者对于人群疏散的影响也不同。

3.4.2 烟气扩散频率的影响

本组参数分析取扩散频率hs={3,6,9}，消光系数αij取1.15。不同hs对应的系统内剩余人数随时间的变化如图8所示。基本模型的平均疏散步长为508 s，hs为3、6、9元胞/s时的平均疏散步长分别为520、532、557 s。

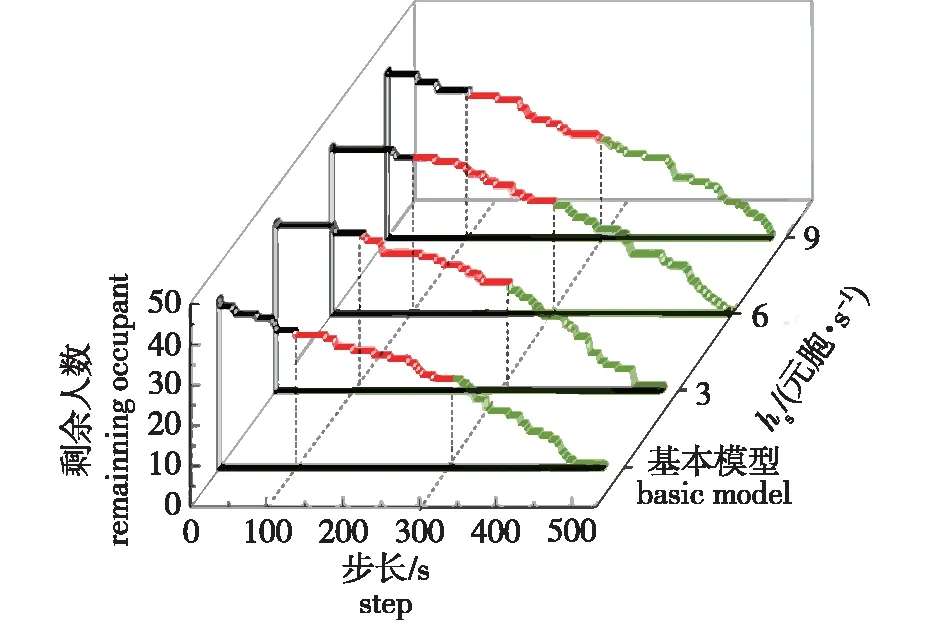
图8 不同扩散频率对应的剩余人数变化曲线Fig.8 Variation curves of remaining occupants related to different hs

当模拟步长小于100 s时，成功疏散的行人受到烟气影响较小，因隧道纵向狭长的空间，需要一段时间到达出口。而当步长大于100 s，扩散频率取3元胞/s时，剩余人数随时间的变化曲线与基本模型几乎一致，说明当烟气扩散频率较小时，主要是静态场强和移动速度影响行人的疏散效率；当扩散频率进一步扩大到6元胞/s时，行人疏散受到烟气影响显著，动态场强进一步影响移动概率，单位时间内成功疏散到出口的人数减少，以至于曲线出现偏移现象。

需要经过100 s的时间烟气扩散频率扩大到6元胞/s时，才能对疏散产生一定的影响。在模拟实例的物理环境中，引入烟气扩散频率能够体现在疏散过程中行人受到的动态场强造成的迂回移动。

基于上述分析，从仿真结果的角度，在改进模型后，疏散人群的实际移动情况与平均疏散步长能够很好地贴合，且在林区隧道烟气环境中疏散时，增加的“烟气扩散频率”概念描述了烟气扩散较慢时，是出口距离和人群移动速度影响人群的疏散效率，而当扩散频率较快时，受到烟气影响显著，说明改进后的疏散模型的仿真过程和结果更接近于实际疏散情况。因此，在实际的林区隧道烟气环境中，应当在隧道内设置穿透性较强的自发光标志，尤其是隧道出入口设置醒目的标志。从计算机的运算复杂度的角度，本研究的模型采用了与传统模型相同的并行更新规则，引入了消光系数来描述烟气对距离感知的影响，采用烟气场强来描述行人在烟气中的逃生行为，因此本研究的模型要比传统的模型运算复杂度高一些。但和社会力模型、排队论模型相比，本研究使用的模型是离散模型，并未引入积分微分等复杂的运算，每次仿真时间较短，占用内存较少，可进行重复计算，也可大量增加疏散的人数，随时中断修改参数以研究疏散情况。