基于手绘草图的快速植物建模

何振邦 程章林

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100049)

1 引 言

植物作为现实世界中常见的自然景观，其三维模型在影视特效、电子游戏和虚拟现实等场景中具有广泛的应用。然而，由于植物具有复杂的结构和多变的外形，植物三维模型的构建一直较为困难。传统的植物建模方法是创作者利用Maya 等三维建模软件以真实的植物图片或实物作为参考，进行细致地手工建模。但这种方法繁琐且低效，尤其是对大规模的植物场景进行建模时，任务会变得更艰巨。因此，高效、快速的植物建模方法一直是计算机图形学研究中一个具有挑战性的重要课题。本文提出一种基于手绘草图的高效植物建模方法。此外，鉴于传统植物建模方法主要聚焦于大型树木植物，对花卉等细小植物的精细结构建模研究较少，本文针对该类细小植物也进行了建模研究。

自 20 世纪 80 年代以来，研究人员和学者发展了许多有效的植物建模方法，如基于规则的过程式建模方法，基于视频图像和三维点云的重建方法，以及基于手绘草图的建模方法[1]等。其中，基于手绘草图的建模方法作为一种新颖、高效的建模方法，近年来得到许多学者的广泛关注。与其他方法相比，基于手绘草图的三维建模方法快速、简便、灵活，创作者可以根据自己的想法绘制草图并快速生成期望的模型，极大地提高建模效率。此外，其他建模方法如基于规则的建模方法较难控制植物外形，需要创作者具有丰富的植物学专业知识且熟悉各种参数的调控方法才能得到理想的目标模型，且模型生成后存在不易修改等问题。但基于手绘草图的建模方法能给创作者较大的自由度去生成各种外形复杂的植物模型而无需了解模型生成的相关细节。因此，基于手绘草图的建模是一种具有较大应用前景的建模方式。

从二维草图中构建植物模型，首先需要从二维草图中提取各种笔画特征，分析草图各部分的语义信息并理解创作者的创作意图，以此为导向进行后续的处理。然而，由二维草图得到三维模型过程不可避免地要面临深度信息缺失的问题，这也是所有基于草图的三维建模方法的难题。因此正确的深度信息对于生成具有较强真实感的植物模型具有至关重要的作用。另外，草图仅提供了植物的大致轮廓信息，如何根据粗糙草图进行相应细节的补充和润色，使最终产生的模型符合自然规律且具有一定真实感，也是基于手绘草图的建模方法需要解决的问题。

本文提出一种基于手绘草图的快速植物建模方法，支持对包括花卉、盆栽、树木等具有花朵、叶片和枝干的植物进行快速建模，弥补了传统方法仅支持单一种类植物建模的缺点，且模型构建过程完全自动化，无需额外的调整信息。算法首先根据草图自动推测建模者的建模意图；然后依靠基于植物学先验知识的模型来恢复植物各结构的深度信息，并根据植物的特点设计模型的优化算法；最后构建出具有一定真实感的植物模型。实验结果表明，本文方法可以构建出具有真实感的各种植物模型，且相比于传统方法，在建模速度上有明显优势。

2 相关工作

2.1 基于规则的过程式植物建模

基于规则的过程式建模方法是最早被提出和应用的植物建模方法。早期的过程式建模方法主要依据植物枝干的生长特性所提出的几何规则来构建植物模型，如枝干的角度、长度比例等[2]。Lindenmayer[3]通过观察植物枝干的分形结构提出 L-System 文法系统[4]——一个基于字符串的替换和重写系统。该系统反复使用不同的规则来生成字符串，通过这种模拟植物的生长的方式来构造分形结构。Prusinkiewicz[5]提出对字符赋予一定的图形的意义来解释这些字符串，从而使得L-System 能用来表达植物模型。

L-System 具有很强的表达能力，能够描述各种复杂的植物结构。但其对于普通用户来说并不友好，需要一定的数学和植物学专业背景知识。鉴于 L-System 难以控制植物的整体轮廓外形，有学者对模型进行逆向推测来获得 L-System 的模型参数[6]，亦有学者通过改进 L-System 来产生外形可控的植物模型[7]。由于现实中的植物还存在空间竞争、趋光性等特点，仅使用 L-System 无法模拟这种行为。Runions 等[8]提出一种空间殖民地算法来模拟树木生长的竞争过程。Palubicki 等[9]提出一种将叶序等植物学因素加以考虑的自组织算法，使生成的模型更为逼真、自然。此外，Yi 等[10]提出一种基于生长方程约束的植物建模方法，来模拟环境阻挡以及不同植物之间的空间竞争等因素对植物生长形态造成的影响。Wang 等[11]提出一种基于部件的快速花朵建模方法：用户可通过输入参数来生成一些预定义的花朵部件，并通过指定部件的组装方式来生成模型，同时花瓣和叶片的纹理也可以根据预设样式自动生成。

2.2 基于真实数据的植物建模

随着硬件技术的发展，高精度的植物图像和点云数据变得越来越容易获取，这为基于真实数据的植物建模提供了便利。Shlyakhter 等[12]提出一种基于照片的树木三维重建方法——通过提取照片内树木轮廓作为参考来生成树木主干，再结合 L-System 形成枝干分支来重建照片中的树木模型。Tan 等[13]提出一种基于单张照片重建树木模型的方法——以追踪图片中可见的树木主干为基础，结合树木轮廓，提出一种数据驱动的吸引子生长方法来补充被树叶遮挡的树枝部分。Guo 等[14]利用过程式建模方法从拍摄的多张植物照片中重建出具有逼真外形的植物模型。Yan 等[15]结合一定的先验知识从单张照片对花卉进行三维重建：假定花瓣围成一个三维圆锥且花瓣尖端围成的椭圆是三维圆锥在图像平面的投影，从而可以利用几何关系还原各个花瓣的大致三维位置。

由于现实场景中各种物体存在遮挡和测量角度限制，加之植物自遮挡现象，三维扫描获取的点云数据不完整且有噪声，如何从低质量的点云数据中重建植物模型具有不小的挑战。Xu 等[16]提出对点云数据进行带权图的构造，并使用最小路径算法结合一定的植物学先验知识进行骨架结构的提取。Livny 等[17]提出一种轻量级的树木表达方式，从杂乱的点云数据中提取较为清晰的主干骨架，而对于噪声较多的树叶部分采用 Lobe的结构表达——使用预储存的样本枝干进行填充，这比直接从点云数据构建树木模型更快速且占用的空间更小。此外，通过在 Lobe 内使用不同填充率还能完成不同层次的渲染。

2.3 基于草图的植物建模

从现实场景重建现实世界的植物有时并不能满足人们的需求，而基于手绘草图的植物建模方法允许人们以直观的方式表达其建模意图，从而能够自由创建生活中不存在的植物模型。草图建模最早于 1999 年由 Igarashi 等[18]在开发基于手绘草图的三维建模软件 Teddy 时提出，该系统根据草图轮廓进行膨胀来产生低复杂度的三维模型。Okabe 等[19]最早提出将手绘草图建模应用在树木建模上，并设计了一个交互式系统来帮助用户将草图生成真实的树木模型，该系统可以在 10 min 内从草图中构建一棵树的三维模型。Anastacio 等[20]提出使用基于构造线的概念草图方式去定义植物器官的排列顺序以及全局结构，而局部使用 L-System进行细节创建。Ijiri 等[21]也提出使用草图进行树木整体结构与轮廓的控制，并结合 L-System 进行局部枝干生成的树木建模算法。Longay 等[22]在平板电脑上实现了一个手绘树木建模系统，该系统结合了过程式建模和自组织建模方法，可以根据手绘草图模拟树木生长，产生真实的树木模型。Ijiri 等[23]还将手绘草图建模应用在花卉建模上，开发出根据手绘花卉草图和花序图进行建模的交互式花卉建模系统。唐棣等[24]提出一种素描式三维花朵建模方法，通过提取草图中的侧影线与边界轮廓线等笔画信息计算出花瓣的横截曲线来构造花瓣的曲面形状。濮群等[25]针对现有花朵建模方法形成的花瓣式样与形态单一的缺陷，提出先根据手绘花瓣的轮廓图提取花瓣模型的二维控制点，然后通过弯曲控制函数得到花瓣的三维控制点，继而利用三维控制点构造三维花瓣模型的方法。目前，大部分基于手绘草图的植物建模工作往往针对单一类型植物，鲜有支持多类型植物的建模方法。

3 草图预处理

对输入草图进行预处理是本文系统的第一步。受限于绘制水平与绘制设备的输入精度，创作者在绘制草图时常常会出现一些微小失误，如笔划的抖动。若不对其进行适当处理，这些绘制失误则会被如实反映到模型中，从而影响模型的质感。此外，从输入设备直接得到的草图采样点可能存在数据冗余和采样点分布不均等问题，不利于后续步骤的处理。因此，对草图进行预处理是十分必要的。

3.1 草图重采样

由于计算机只能处理离散数据，而从输入设备中得到的草图笔划实际上是一系列的离散点集合，且输入设备的采样率较高、采样点较为密集，存在一定的冗余数据，会影响后续算法的处理速度。此外，若创作者在绘图时移动光标的速度不均，可能出现采样点分布不均的情况。因此，为了简化笔划信息、获得间隔均匀的像素点，在预处理步骤中，本文首先对笔划进行的重采样，即先按次序连接笔划中的所有采样点以形成笔划线段，然后从首点出发，沿线段以一定半径对笔划线段上的点进行重新采样，以获得均匀的新采样点。

3.2 草图平滑

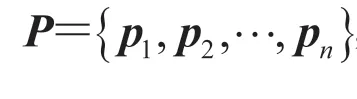
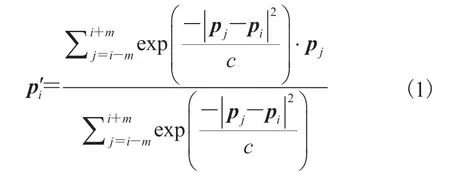
其中，m为对采样点进行平滑处理的窗口半径；c为权重影响因子。

4 草图分析

预处理后的草图只是一些采样点集合，所包含的信息十分有限，因此需要对这些点集进行图元分类，并对图元进行语义分析，以推测创作者的创作意图，最终得到建模对象类别和相关的参数信息，并提供给后续步骤进行模型构建操作。

4.1 图元分类

在获取草图时要充分考虑系统给予创作者的自由度与便利性，同时也要兼顾后续处理的难易度。因此，文本方法约定输入的图元类型有 5种：花瓣、叶片、枝干、枝干轮廓和叶片轮廓，各图元示意简图如图 1 所示。各图元的具体定义如下：叶片是具有近似闭环结构的曲线；花瓣可以看作是一种特殊的叶片，即若干互相聚集的叶片；枝干是多个非封闭曲线的集合；枝干轮廓是围绕枝干的曲线，定义了植物内部细枝干的生长范围和大致轮廓；叶片轮廓也是围绕枝干的曲线，定义了植物内部叶片填充的范围和大致轮廓。

图1 草图中支持绘制的各图元示意简图Fig.1 The sketch elements supported in our system

枝干轮廓和叶片轮廓分别在特定模式下绘制，故无需进行进一步的分类。而花瓣、叶片、枝干均在部件模式下绘制，为了能够分别对花瓣、叶片和枝干进行建模，需要将部件模式下绘制的笔划进行分类。鉴于花瓣和叶片在二维形态上是相似的，仅存在纹理以及空间位置上的不同，本文方法将花瓣和叶片的细分类留到后续的步骤中进行，在元素模式下仅需要将绘制的笔划分成花瓣和叶片一类，以及枝干一类。本文使用支持向量机根据提取的笔划特征进行分类。参与分类的特征有：(1)笔划起点到终点的距离与整个笔划长度的比值；(2)对笔划采样点进行主成分分析(Principal Component Analysis)后得到的较大特征值与较小特征值的比值；(3)对笔划采样点主成分分析后得到的两特征向量方向上形成的包围盒的面积与笔划长度的比值。本文预先绘制和标注了约 200 个笔划数据，并使用支持向量机训练一个分类模型来进行笔划分类。

将花瓣和叶片与枝干区分后，需要对花瓣和叶片作进一步分类。本文的花瓣和叶片分类算法是基于以下观察假设：自然界中同属于一朵花的花瓣是由同一个原基区域发育而来，花瓣的根点彼此靠近以形成所谓的花心，而叶片则通常从枝干的侧面单独生长发育而来，少有叶片的根点互相聚集。因此，可对叶片和花瓣的根点进行聚类，将互相聚集的花瓣和单独分布的叶片分类开来。本文并未要求创作者指定花朵的数目，聚类簇的数目是未知的，因此本文使用 Mean Shift 算法对花瓣和叶片的根点进行聚类。聚类后簇中元素个数＞2 的簇被分类为花朵，元素个数≤2 的簇则被分类为叶片。

4.2 枝干层级分析

前述步骤已完成枝干分类，在对枝干进行建模时，通过枝干的父子层级关系调整枝干的半径、延伸方向和姿态等参数可增强模型的真实感。本文设计了一个算法可对这些枝干进行父子层级分析，定义处理集 M 和未处理集 N，初始状态下所有枝干都在集合 N 中。算法首先从集合N 中取出最长的枝干作为 0 级节点移入集合 M；随后遍历集合 N 中所有的枝干，与当前集合 M中所有属于最大层级的枝干进行匹配，若集合 N中枝干nj的端点与集合 M 中属于最大层级的枝干mi的点集内任意一点的欧几里得距离最小且该距离小于阈值，则nj与mi匹配，即nj为mi的下一层级，mi为nj的父节点，并将nj从集合 N移入集合 M；重复上述操作直到集合 N 为空集或集合 N 内无枝干可以匹配。

4.3 区域填充

当创作者期望描述一个密集的细枝干簇结构时，本文系统允许创作者在待分枝的主枝干周围绘制一个轮廓笔划，代表轮廓内有许多细枝干从主枝干生成，且生成的新枝干簇整体轮廓与笔划大致相符。为了完成此目标，系统需要在轮廓范围内进行细枝干填充，本文参考 Tan 等[13]基于单张照片的树木建模工作中提出的数据驱动的吸引子算法。首先，对枝干进行采样得到若干生长点，同时对轮廓进行采样得到若干吸引点。然后，从某一生长点出发行进，设当前点为pi，则下一点的坐标pi＋1为：

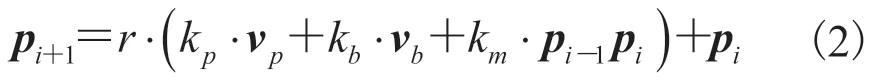
其中，kp为轮廓吸引系数，vp为当前生长点指向轮廓上最近吸引点的方向；kb为枝干吸引系数，vb为细枝干初始生长点所附着处的父枝干方向；km为方向记忆系数，pi－1pi为上一生长点指向当前生长点的方向；r为总体生长速率。重复迭代该过程直到当前生长点已靠近轮廓笔划。该公式综合考虑了轮廓吸引方向、细枝干附着的父枝干方向以及前一生长方向的影响，可通过设置不同的参数达到不同的生长效果。其中，不同参数对枝干的形态影响如图 2 所示。

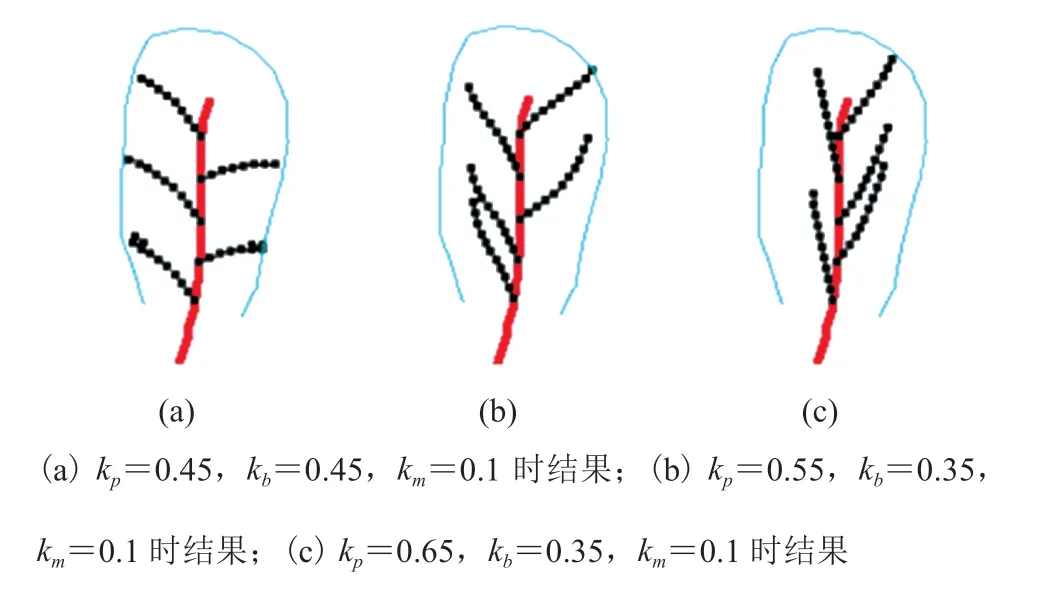
图2 不同参数对枝干形态影响图Fig.2 The impact of different parameters on the branch shapes

当创作者需要在一个枝干周围布满叶片时，可以在该枝干的周围绘制一个轮廓笔划，代表枝干上生长有与轮廓形状相符的叶片簇。与枝干填充算法类似，叶片轮廓填充算法先按照枝干填充算法生长出一个主叶脉结构；然后，在已绘制叶片中随机选择一个模板叶片执行仿射变换，并与主叶脉对齐——使仿射变换后的叶片的根点与主叶脉初始生长点对齐，同时该叶片的尖点(叶片笔划中曲率变化最大的点，即视觉上叶片最为突出的一点)与主叶脉的末点对齐。由此得到新叶片并将该新叶片加入当前叶片集合中去，该过程如图 3 所示。

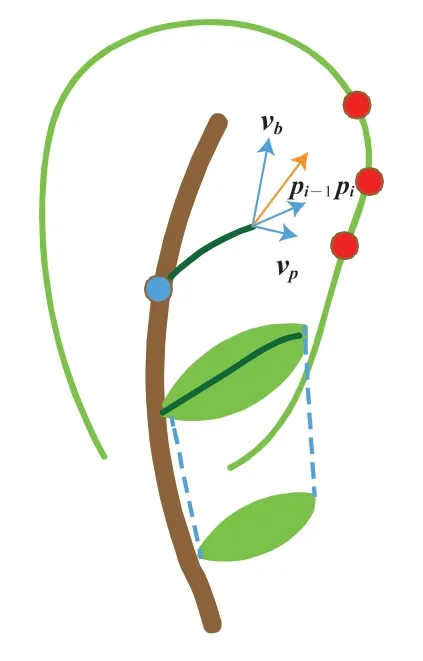
图3 叶片生长和填充过程示意图Fig.3 An illustration of the leaf growth and fill

5 深度恢复

基于草图建模技术最关键的问题是如何从二维图像中恢复深度信息。由于二维草图存在深度信息的缺失，用二维草图表示三维模型具有歧义性，即草图中的二维投影所对应的深度可以有无数种可能，如何找到一个合理的二维-三维映射是一项巨大的挑战。因此，在三维模型的逆向推测过程中需要结合一定的先验知识，以保证逆向推测得到的三维模型的合理性。本文以植物学知识为向导，结合对真实植物样本的观察，提出一定假设与约束来分别对花朵、枝干、叶片进行深度信息的恢复。

5.1 基于圆锥假设的花朵深度恢复

通过观察大量的花朵实物样本并参考 Yan等[15]相关工作，本文使用一个圆锥模型来恢复花朵的深度信息，即认为由若干花瓣组成的花朵是高度对称的：花瓣环绕花心近似形成一个圆锥，且圆锥的顶点位于花心处，花瓣大致贴合在圆锥侧面上，各个花瓣的尖点围成圆锥底面圆。其中，花瓣的尖点定义为笔划中曲率变化最大的点，视觉上是花瓣最外围的一点，如图 4(a)所示。

本文假设草图是由花朵实体经过垂直于绘图屏幕方向的平行投影所得，因此，通过分析草图中每朵花的花瓣形成的圆锥投影可以得到三维空间圆锥的方程，从而代入各花瓣上采样点的XY二维坐标解得花瓣的Z轴深度信息。

本文花朵深度信息恢复算法如下：

(1)计算当前处理的花朵中所有花瓣的根点坐标均值，记为花心cf。

(2)使用最小二乘法对所有花瓣的尖点进行椭圆拟合，得到椭圆E。

(3)根据假设，二维草图是通过垂直于绘图屏幕方向的平行投影得到的。因此，椭圆E的长轴即为原三维空间中圆锥底面半径r，圆锥的主轴与绘图平面所成的夹角θ有 sinθ＝a/b。其中，a、b为椭圆E的短轴和长轴，根据此关系可求得θ。

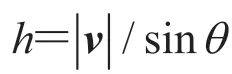
(5)步骤(4)中所得椭圆方程是以Z轴为圆锥主轴的标准形式，未考虑椭圆旋转角θ。为了计算旋转矩阵，以花心cf为原点建立三维直角坐标系。设垂直草图平面的单位向量z＝[0, 0, 1]，可计算得到椭圆的旋转轴vn＝v×z。已知圆锥主轴与草图平面的夹角θ，可计算通过绕vn旋转使得圆锥主轴与Z轴重合的旋转矩阵RM，如图 4(d)所示。

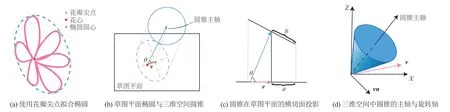
图4 花朵的深度信息恢复算法示意图Fig.4 An illustration of the flower depth recovery algorithm

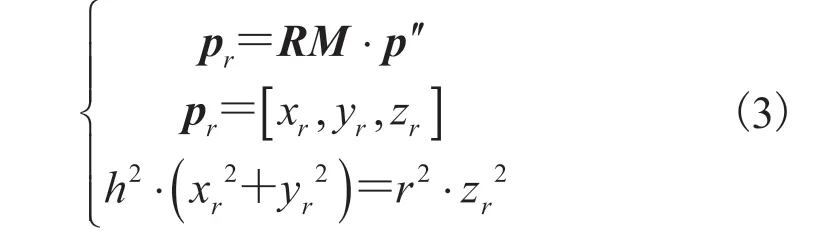
其中，pr为点 通过旋转矩阵RM变换到以Z轴为主轴的标准圆锥方程中的点坐标。

5.2 基于最大熵的枝干深度恢复

枝干的几何结构较为简单，只需知道枝干两端点的深度信息便可通过插值得到枝干上各点的深度。本文参考 Okabe 等[19]的基于草图的树木建模工作，设计了一种获取枝干深度的算法。算法的主要思想是基于之前得到的枝干父子层级关系，让所有子枝围绕其父枝旋转，以寻找一种枝干的三维分布状态——在该状态下，枝干的熵(即分布的散乱程度)最大，枝干在三维空间形成均匀、自然的分布效果。同时还对枝干的旋转角度进行一定约束，避免较大的旋转角导致旋转后的三维空间枝干长度与草图空间枝干长度的差值过大，显得过于突兀。对于某一枝干b，其熵S(b)的定义参考公式(4)：

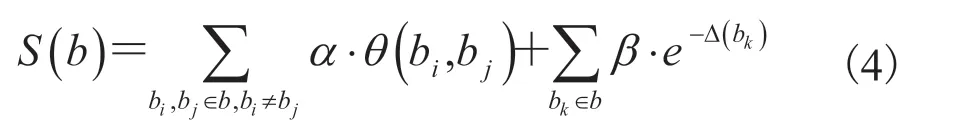
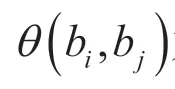
本文算法是递归进行的，处理完某枝干后再以相同方法处理其子节点。考虑当前枝干作为父枝干，将子枝干分成左侧的子枝干和右侧的子枝干两组，给予每个子枝干一个服从高斯分布的随机扰动角度作为初始值，应用最优化方法求解当前枝干熵最大时的子枝干旋转角度。在实际操作中，通常经过最优化算法的多次迭代计算后便可得到具有较好效果的旋转值，而无需解出最大熵值下的最优分布。值得注意的是，若不对子枝干进行左右区分，则可能出现某个子枝干得到一个较大的旋转角，使得该枝干从一个半球旋转到另一个半球空间内，造成与原二维草图表达意图相冲突的问题。根据三维空间的旋转角度可以从二维投影坐标反解出三维空间的Z轴深度值，从而实现深度信息的获取。图 5 展示了利用本文算法恢复深度信息重建得到的三维枝干模型。

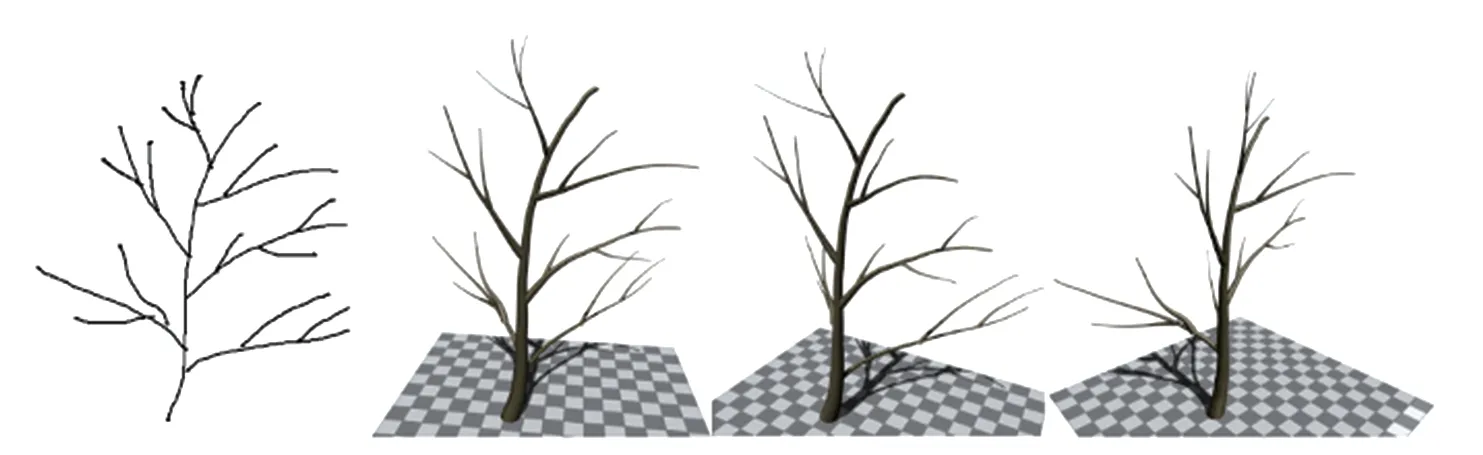
图5 利用枝干深度信息重建得到枝干模型Fig.5 The reconstructed branch model using recovered depth

5.3 基于先验的叶片深度恢复

由于叶片的生长较为自由，相关工作中也鲜有对叶片的草图建模研究，这对叶片的深度信息获取提出了一定挑战。鉴于叶片通常由枝干旁的小芽发育而来，且叶片作为植物养分生产器官总是趋向于接触到最多阳光的方向生长，因此叶片在大部分情况下位于垂直于阳光的平面上。此外，由于创作者在草图绘制的方式上不太可能使用精确的透视手法，即绘制的叶片草图仅描绘叶片的轮廓形状，而不代表特定的三维位置信息。

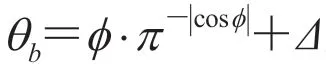
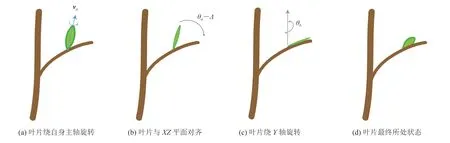
图6 叶片深度信息获取示意图Fig.6 An illustration of the leaf depth recover

6 模型构建与优化

在获得草图中各部分的深度信息之后，便可以通过 Delaunay 三角化进行网格模型的生成。由于植物的结构较为复杂、曲面形状多变，因此在建模时应充分考虑这些特点并呈现在模型中以增加模型的真实感。

6.1 花瓣弯曲模拟

花瓣弯曲广泛存在于各种类型的花朵中，其中有的是受重力影响，也有的是因花瓣固有的形态所致。本文认为花瓣是一个软体平面，满足弹性力学原理。根据力学的相关知识可以推出，一个长度为L的理想化软体棒上某点距离底端的长度x与该处弯曲形变y之间的关系有：

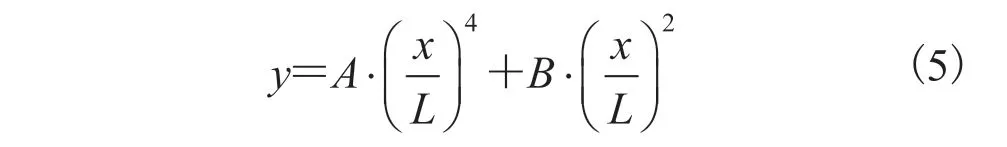
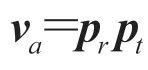
图7 花瓣弯曲模拟结果Fig.7 The result of petal bending modeling

6.2 花瓣内凹模拟

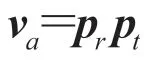
图8 花瓣内凹模拟结果Fig.8 The result of petal hollow modeling

6.3 各级枝干半径确定

在现实世界中可以观察到，植物枝干在分叉后具有不同的半径，且越末级的枝干半径越小。事实上，植物枝干的分支遵循一定的规律。规定每一级枝干的半径在各处都是一致的，设r为分支点处父枝干的半径， 为分支点以上各子枝干的半径，则满足：

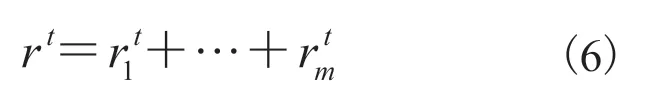
其中，幂级数t控制枝干半径积累程度，影响下一级枝干半径的相对粗细，且不同植物有不同的幂级数t。当t＝2 时，即为达芬奇提出的树木分支枝干半径关系；对于花卉等草本植物，取t＞2 可达到较好的效果。在草图分析步骤中，基于枝干间的父子层级关系，通过遍历枝干节点可以统计得到某枝干的子节点和子节点个数，将相关信息带入公式(6)可得到子枝干的半径供后续建模参考。

6.4 枝干半径衰减

事实上，植物某一级枝干的半径并不是恒定的。对于一级枝干，其半径从根部到顶端是逐渐衰减的，这是植物生长的先后顺序和生长累积效应造成的。为了捕捉这种现象，本文提出半径衰减公式(7)，在距离根部长度与枝干总长的比值为x处的半径衰减比值r为：

其中，s和α控制衰减的快慢，s一般取s＞10，α一般取 0.3～0.5；m控制枝干末端半径与根部半径的比值，一般取 0～1。

6.5 枝干的几何形体建模

目前，对于植物枝干的几何形体建模已有广泛的研究，常用的枝干描述方法有多棱柱、B 样条曲线、广义圆柱等。基于建模和渲染的综合性能考虑，本文默认使用八棱柱来对枝干进行建模：将一个正八边形的中心沿着枝干骨架移动放样，同时参考前文步骤中各级枝干的半径和半径衰减公式来调整八边形的半径。若建模时枝干设置的初始半径较大时，可增加棱柱边数以提高模型精度，并达到较好的视觉效果。

7 结果与分析

本文使用 C++ 实现上述算法，使用 Qt 作为图形界面框架并使用 OpenGL 进行模型的渲染显示，实现的系统界面如图 9 所示，创作者可在界面左侧进行草图绘制，并在右侧实时观察生成的模型。为了测试本文方法建模的有效性，在一台配置为 8 GB 内存、2.4 GHz 主频双核 CPU 的电脑上对建模算法进行若干测试实验。

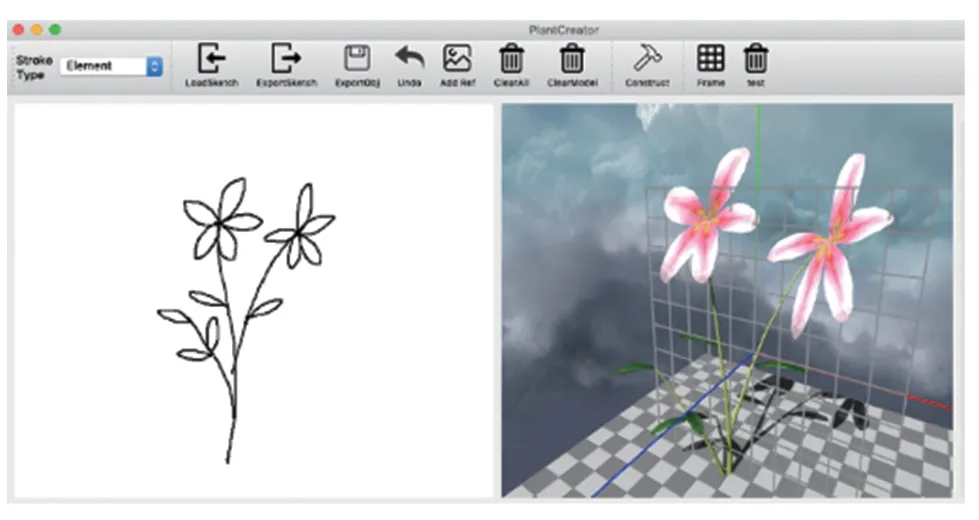
图9 本文基于手绘草图的植物建模系统界面Fig.9 The interface of our sketch-based plant modeling system

实验首先测试了本文方法建模的有效性和效率，即邀请 6 位未使用过本系统的用户进行手绘草图建模。在测试前，先对用户进行简要地介绍与指导；随后，用户在程序中自由进行草图的绘制并使用系统进行建模，直到用户构建出满意的模型，同时记录下建立 8 个不同种类和规模的植物模型所用时间与相应的模型参数。测试中的草图和模型如图 10 所示，植物模型的属性和建模时间如表 1 所示。由表中数据可知，对不同规模和种类的植物模型，本文系统具有较高的效率，均能在 1 s 内完成模型构建；用户也一般能在 2 min 完成整个草图绘制、调整与模型构建的过程，并得到满意的建模结果。总体而言，本文系统的建模速度主要与草图处理后得到的图元数量成线性关系，由于本文系统支持轮廓填充，可生成更多的枝干或叶片，因此较少的笔划也可能导致较长的处理时间。整个处理流程，二维草图的处理耗时较短，深度恢复和模型三角化占据了大部分处理时间。草图处理后得到的枝干、叶片和花瓣越多，处理时间越长。由于需要对叶片和花瓣进行形态模拟，较少的顶点数会导致较差的花瓣弯曲和内凹视觉观感，因此叶片和花瓣的顶点分布较为密集，具有较多该类图元的模型拥有的顶点数和三角面数也较多。另外，叶片和花瓣的处理时间显著长于枝干的时间，这是由于叶片和花瓣具有较多的顶点数，三角化需要的时间更长，且在建模时会进行额外的形态模拟。如图 10 和表 1 中模型(c、e、g、h)所示，这 4 幅草图中的叶片和花朵较多，特别是模型(g、h)为含有较多叶片的大型树木，相较于其他模型处理时间显著增长。

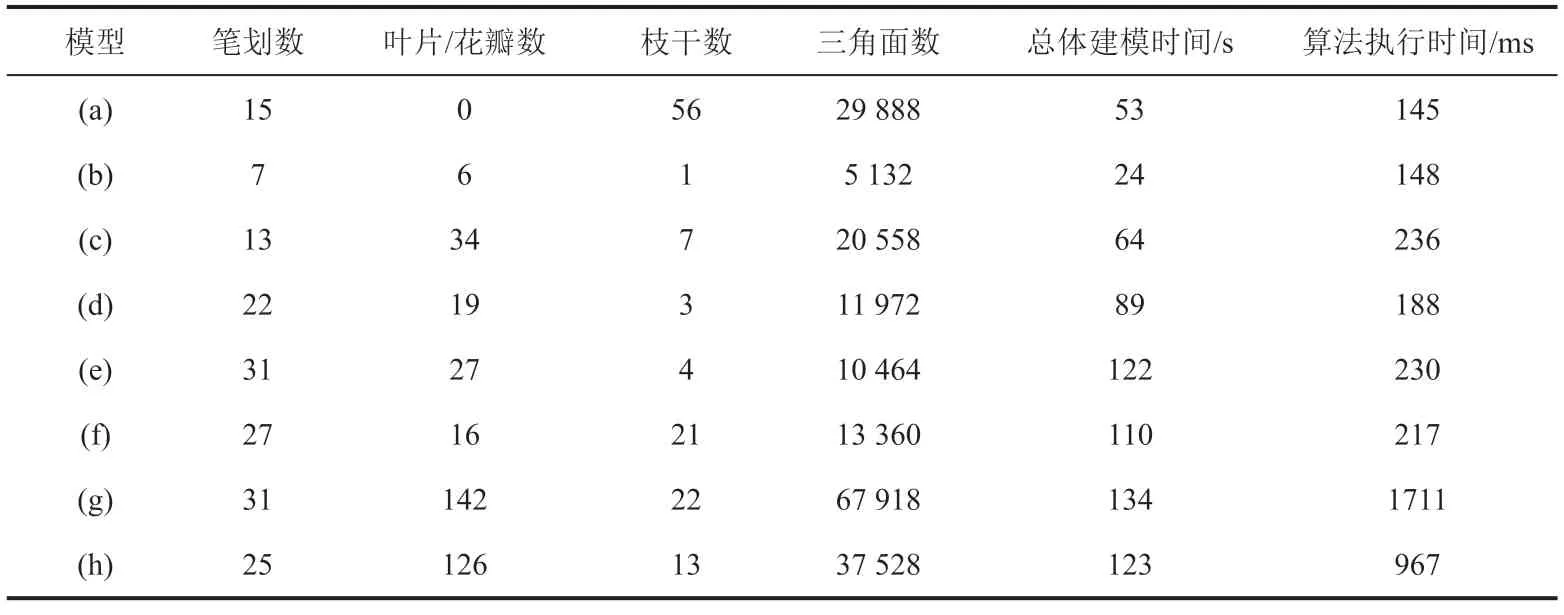
表1 植物模型的数据统计Table 1 Statistics on tested plant models

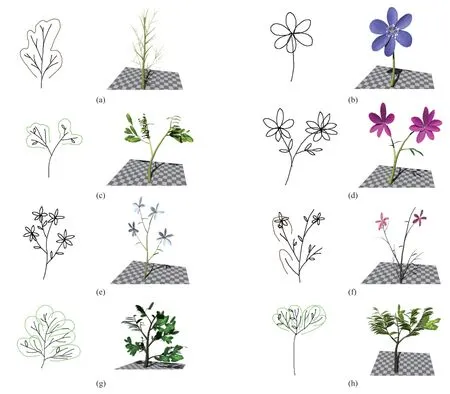
图10 实验中用户绘制的草图和得到的模型Fig.10 The sketches and constructed models in our test

为了展示本文方法所构建模型的真实感，本文还根据真实图片进行手绘建模的对照实验。实验收集了若干植物的真实图片，首先根据真实图片进行手绘临摹出草图，然后使用本文系统进行建模，并将真实图片中手工提取的纹理映射到所建立的模型上，实验结果如图 11 所示。从对比图可以看出，本文方法能够较好地还原植物的各种形态与细节，且构建的模型生动、形象，具有一定的真实感。

图11 根据真实植物图片临摹草图并重建得到的植物模型Fig.11 The reconstructed plane models according to real plane photos

横向对比其他学者的植物建模系统，唐棣等[24]的花朵建模系统需要绘制花朵的侧影线来确定花朵的三维结构，这对创作者的绘制水平提出了不小要求，本文方法无需用户精确绘制投影视角下的草图；濮群等[25]提出的基于手绘花瓣的花朵建模方法虽然允许用户通过绘制花瓣草图来进行建模，但仍然要求用户对花瓣轴线上的控制点进行控制来调整花朵形态，同时该方法涉及的参数较多，提高了操作的门槛；缪永伟等[26]提出的基于对称性的单幅图像花朵建模允许用户在已有图像上绘制花朵轮廓来进行建模，与本文方法相比，该方法仅支持对单个花朵进行建模，无法构建出具有枝干、叶片的完整花朵模型。本文方法与前述方法在花朵建模方面的效果对比如图 12所示。对比参考图像，本文方法构建的花朵具有较为还原的形态。相较于其他基于手绘草图的树木建模系统，Okabe 等[19]的系统需要细致地绘制叶片并手工排列叶片分布，而本文方法仅需要绘制若干模板叶片即可，算法会进行自动复制和填充；马玲等[27]的系统由于预先建立了枝叶数据库，仅需要绘制几笔草图便可快速得到树木模型，具有较高效率，然而其结果对树木的形态控制不佳，图 13 展示了该方法与本文方法在输入相似草图时的结果。总体而言，与传统的交互式建模方法相比，本文方法大大降低了用户的工作量，与现有的草图建模方法相比，本文方法不局限于单一树木或花朵的建模，可以通过自由组合各种图元来建立多种植物模型，为用户提供较大的创作自由度。

图12 不同方法的花朵建模结果对比Fig.12 The flower reconstruction result comparison on different methods

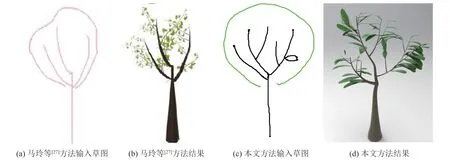
图13 不同方法的树木建模结果对比Fig.13 The tree reconstruction result comparison on different methods

8 结 论

基于手绘草图的植物建模方法作为一种直观、快速、便捷的建模手段，面对植物这种具有复杂形态、传统方式处理繁琐的建模对象，在建模效率上有突出的优势。然而，从深度信息缺失的二维草图中重建出符合创作者意图的三维植物模型一直是基于草图建模需要解决的难点。本文提出一种基于手绘草图的快速植物建模方法，能够自动地从绘制的二维草图中建立出花朵、盆栽、树木等具有枝叶结构的植物模型。本文方法通过结合植物学先验知识来辅助深度信息的恢复，其推断和重建出的植物结构较为自然且符合二维草图的形态描述。同时本文还对植物的形态细节进行了建模，产生的模型具有一定的真实感。与其他同类基于手绘草图的植物建模方法相比，本文方法支持的图元类型较多，能够通过组合图元来创作各种形态的植物模型，而不局限于单一种类的树木或花朵。

本文系统还存在一些不足，如仅支持花瓣、叶片和枝干这 3 种植物元素，后续可以增加如根、花蕊、果实等元素。由于本文方法对花朵的建模依赖于圆锥模型假设，处理形态较为复杂、具有较多层级和自遮挡的花朵模型时，难以对花朵形态进行较为忠实地还原。此外，由于先验知识模型的局限，本文系统生成的植物模型姿态较为单一，在后续的研究中可以结合更多的植物学知识，如参考趋光性、重力、自组织生长、空间竞争等因素来生成更为自然逼真、多姿多态的植物模型。近年来，植物建模研究的一大趋势是将传统的植物建模方法与机器学习、深度学习方法进行结合，在后续研究中可以考虑将这两种方法用于辅助深度信息的恢复、植物种类的识别和分类、纹理的生成等。