平面二维数学模型在土石坝溃坝洪水演进中的应用

曹 伟

（山西省水利发展中心，山西 太原 030002）

1 概况

庄头水库位于山西省长治市壶关县晋庄镇庄头村南，浊漳南源支流石子河上游，是一座多功能综合利用的中型水库，1977年10月建成，控制流域面积119.1 km2，总库容1 675万m3。大坝为均质土坝，最大坝高44 m，坝顶长300 m，宽5 m。开敞式溢洪道，堰顶高程1 083 m，宽17 m，最大泄量779 m3/s。水库设计洪水标准为100年一遇，校核洪水标准为300年一遇。庄头水库下游保护区有两个乡镇六个村庄，20余个企业及长治市区。保护耕地300余hm2，大畜1 000余头及杜家河、河口、闫家河、王家河、坛上等村1 300余间房屋，长平公路、长新铁路的安全畅通，还保障下游石子河水库的安全度汛。

2 模型原理与方法

采用土石坝溃坝统一公式，计算溃坝峰顶流量及流量过程线；使用平面二维水动力数学模型，对溃坝后洪水的演进过程进行模拟，得出不同溃坝情况下的淹没范围及最大淹没水深。

2.1 模型控制方程

数学模型的基本控制方程是二维浅水方程[1，3]：

（1）连续方程：

（2）运动方程：

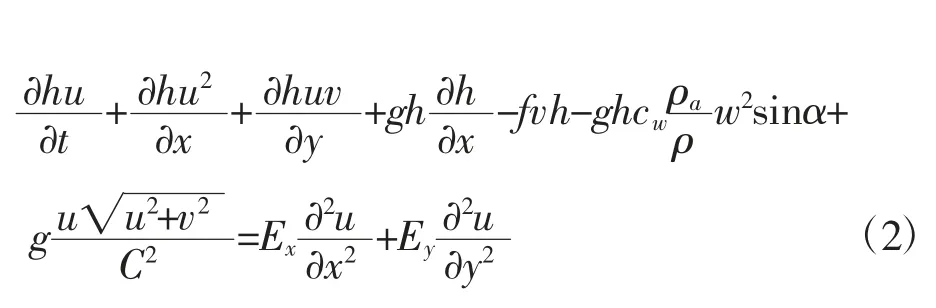
式中：h——水深，m；

t——时间，s；

u，v——沿x和y方向的垂线平均流速，m/s；

x，y——横轴和纵轴坐标；

g——重力加速度，9.8 m/s2；

f——柯氏力系数；

ρ——流体密度，kg/m3；

ρa——参考密度，kg/m3；

cw——风的摩阻系数；

α——风速与y轴的夹角

w——实时风速，m/s；

Ex、Ey——x，y方向的涡粘系数，m2/s；

C——谢才（Chezy）系数；

n——曼宁（Manning）粗糙系数。

在控制方程的求解过程中，使用有限体积法进行离散，采用三角形网格；时间积分采用显式欧拉格式；计算中采用干湿网格方法对浅滩进行考虑。

2.2 溃口流量计算

2.2.1 峰顶流量计算

庄头水库主坝为土石坝，本文主要考虑了在校核洪水位下逐渐溃坝（工况1）及瞬间全溃（工况2）两种工况，采用土石坝溃坝统一公式计算溃口流量[2]：

式中：Qmax——溃坝峰顶流量，m3/s；

λ——流量参数；

g——重力加速度，9.8 m/s2；

bm——最大口门宽度，m；

H0——溃坝前上游水深，m；

W——库容水量，万m3；

K——冲刷系数，%；

E——坝横断面积，m2；

φ——土质系数。

式中：σ、m、f——为沉溺系数、断面形状参数、堰高比；n2、n4、n6——指数；

e——堰宽比；

λe——矩形断面自由出流、口门拉至河底、堰宽比为e时的流量参数。

2.2.2 溃坝流量过程计算

峰前流量过程线计算：

式中：q——峰前流量，m3/s；

βm——溃坝处最大水深比；

n——库容指数，一般为2～2.5，本次取n=2.3；

t——时间，s；

τ——口门达到最大、达到峰顶流量时相应的时间，s；

Qm——峰顶流量，万m3；

E——坝横断面积，m2；

bm——最大口门宽度，m；

ρ——平均体积含砂量百分数；

W总——总库容，万m3；

K——冲刷系数，%；

H——峰前坝前水深，m；

λ——流量参数。

峰后流量过程线可按瞬间溃计算：

式中：W′总——峰后剩余总库容，万m3；

βm——溃坝处最大水深比；

W总——总库容，万m3；

H′0——峰后剩余最大水深，m；

H0——溃坝前上游水深，m。

放空时间按下式计算，近似n=2.5：

式中：t空——放空时间，s；

ξ1——取0.002，即水库放空到的2‰为止；

D2（ξ1）——n=2.5时相应的系数，查表得2.495。

根据相应的n值，可在《溃坝水力学》中查出值，（其中，qi为ti时刻的流量，m3/s；ti为放空期间不同时刻，s。），再根据公式（15）和（16），即可求出峰后流量过程线。

2.2.3 计算结果

（1）工况1：在校核洪水位下逐渐溃坝时，随着溃口宽度从小到大，流量也不断增大，当达到溃坝峰顶流量后又开始减少。最大下泄流量达6 283.66 m3/s，排水总历时2 h：11 min左右。

图1 校核洪水位下逐渐溃坝流量过程线

（2）工况2：在瞬间全溃情况下，由于溃口不存在逐步发展的过程，溃坝流量在开始即达到峰顶，之后随时间逐渐减少。峰顶流量达到23 275 m3/s，溃坝过程历时21 min左右。

各工况下溃口特征参数见表1。

表1 各工况溃口特征参数表

图2 瞬间全溃流量过程线

2.3 模型建立

构建模型时先选定模拟区域地形数据并导入，庄头水库下游地区地形数据是以美国SRTM数据库中下载的90 m精度的数字高程为基础，对散点图进行内插得到模拟区域的地形文件；之后进行地形网格的剖分，本次模拟使用的是非结构化三角形网格，计算时用网格生成器将地形区域分为若干不规则的三角形网格；最后设置模型边界条件及初始条件，选定上游庄头水库大坝处为入流边界，入流边界条件为溃坝流量过程，下游村镇及长治市郊区则采用陆地边界。模型模拟初始时，下游模拟区域无水流，初始条件设置为模拟区域中地面高程最低值，而上边界庄头水库大坝处的初始水位为开始溃坝时的水位值。为保证模型计算的连续性，还需要针对模拟区域动边界设置干水深和湿水深，本次将干水深设置为0.005 m，湿水深为0.1 m，即模型计算过程中水深小于0.005 m的区域不参加计算，水深大于0.1 m的区域参加计算[3]。

模型共1454个网格节点，考虑各方面因素，网格计算时间步长60.0 s，总计算步数为300，即模拟5 h。模拟区域网格划分见图3。

图3 模拟区域网格划分图

3 模拟结果

本次模拟区域地形上游为山区，下游为平原，因而地形高差较大。建立网格文件后，根据水动力模型，逐项输入相应数据，根据计算机性能调试模型，确定各项计算参数，然后进行2种不同工况下溃坝后洪水演进模拟。在本次模型模拟过程中，共选取了洪水演进至下游过程中的6个特征点。分别为：坝址处，闫家河村距离大坝2.56 km，集店乡距离大坝4.89 km，石桥村距离大坝8.15 km，壶口村距离大坝12.66 km，市区距离大坝17.5 km。

3.1 逐渐溃坝

逐渐溃坝不同时间段淹没范围及水深见图4。

图4 逐渐溃坝淹没范围

由淹没范围及动态演进结果分析，对于逐渐溃坝的情况，初始溃坝流量逐渐增大，达到峰值6 284 m3/s后又逐渐减小。逐渐溃时最终口门宽度发展到69.7 m，整个溃坝洪水下泄过程时间较瞬间全溃长，达到2 h多。溃坝开始后10 min内洪水已经到达距离大坝2.56 km的闫家河村。溃坝后洪水在山区地形中继续演进，在1.5 h左右到达距离大坝12.66 km的壶口村，随后开始进入长治市区。根据水位过程线，石桥村位置由于处于山区内位置比较低洼的地带，洪水向下传播过程中，该处的水深最深，峰值达到7 m，并且洪水在20 min内迅速聚集达到峰值水深。对于长治市区特征点，水位从1h：50 min左右开始迅速升高，水深超过2.5 m，5 h模拟结束后，虽然未淹没大部分城区，但市中心低洼地带的局部地区水深较深。

3.2 瞬间全溃

瞬间全溃不同历时淹没范围见图5。

图5 瞬间全溃淹没范围

由淹没范围及动态演进结果分析，对于瞬间全溃的情况，初始溃坝流量大，达到了23 275 m3/s，而且流速也最快，洪水下泄极为迅速，整个库容清空仅用时21 min。距离大坝最近的闫家河村，10 min内被洪水淹没，最大水深达到3.4 m。随后洪水迅速向下游演进，到达距大坝4.89 km的集店乡，乡镇中最大水深达到2.2 m。由于集店乡人口较多，距离大坝较近，受灾损失也比其他村庄严重。而在溃坝5 h后，长治市城区特征点的水位也达到1.8 m。相比于逐渐溃坝的情况，瞬间全溃洪量更大，洪水下泄更加迅速，对下游造成的灾害及影响也要严重很多。

3.3 模型合理性验证

对于溃坝模拟模型，并无实测资料可对其合理性进行验证，本文采用了水量平衡法对结果进行验证。选取工况1，在溃坝后10 min至2 h选定5个固定时间，分别根据溃坝流量过程线计算出下泄洪量，然后与模拟结果进行比较，求出相对误差。验证结果见表2。

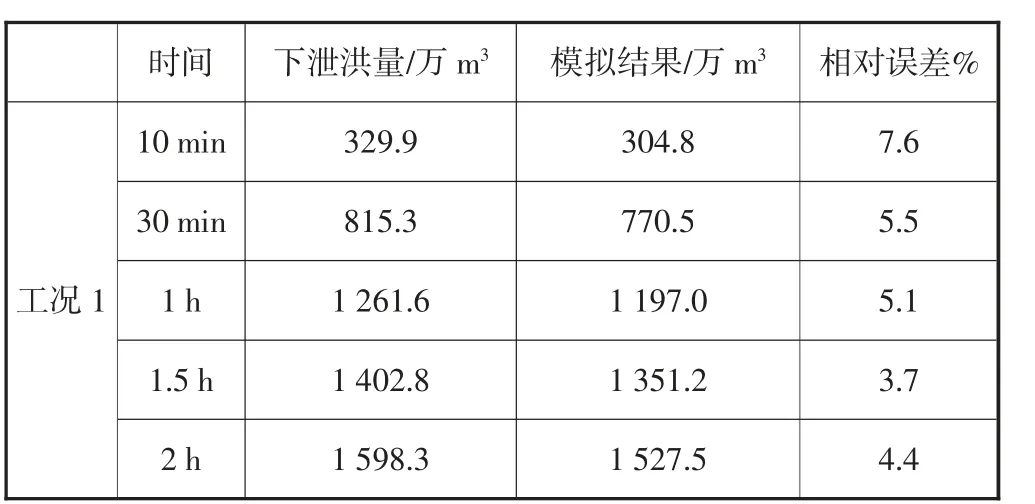
表2 水量平衡验证结果表

由表2可知，不同时间段二者相对误差为3.7%～7.6%，在合理误差范围之内，可见本文的溃坝模型能较好地模拟土石坝溃坝洪水演进过程。

4 结论

基于庄头水库逐渐溃坝和瞬间全溃2种工况，选用经验公式计算出溃坝峰顶流量及流量过程线，利用平面二维数学模型模拟了水库溃坝洪水演进过程。通过对下游特征点水位、流速分析，量化了溃坝洪水演进情况，并用水量平衡法验证了模型的合理性。

大坝的溃决是一种低频率、高风险的灾害，溃坝一旦发生将给下游地区带来灾难性的影响。希望能借此方法帮助人们了解溃坝后相关地区受灾状况及洪水发展动态趋势，能够提前建立疏散及预警机制，将溃坝损失降至最低，以保障人民的生命财产安全。