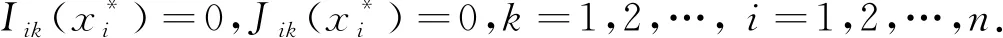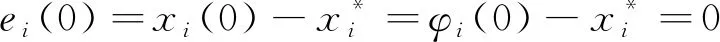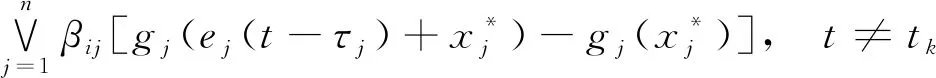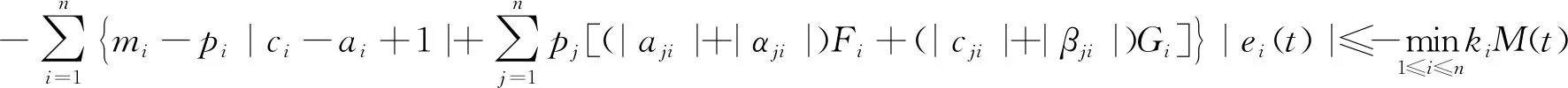具有脉冲效应的时滞Caputo分数阶模糊惯性神经网络的渐近稳定性

王景峰, 柏传志

(淮阴师范学院 数学与统计学院, 江苏 淮安 223300)

0 引言

本文考虑了下列具有脉冲效应的延迟分数阶模糊神经型惯性神经网络

(1)

其中

系统(1)的初值为

xi(s)=φi(s),CDβxi(s)=ψi(s), -τi≤s≤0

(2)

Yang Y和Yang L B于1996年提出模糊细胞神经网络与模糊逻辑和神经网络相结合理论[1]．模糊神经网络更适合并有潜力解决实际的一些问题,在过去几十年中,已经获得了许多关于时滞模糊神经网络稳定性行为的结果[2-7].1986年,Babcock和Westervelt首次在神经网络中引入惯性项[8].在神经网络的实际应用中,这种惯性项的添加会导致更复杂的动力学行为,如分岔和混沌[9].因此,人们对惯性神经网络的稳定性进行了大量的研究,并得出了许多有趣的结果[10-12],如:与整数阶微积分相比,分数阶微积分对各种过程的记忆性和遗传性有更好的描述．分数阶神经网络受到了广泛的关注,作为一个非常重要的问题,分数阶神经网络的动力学行为分析以及平衡点的存在性、唯一性和稳定性在过去几十年中受到了越来越多的关注[13-19].

目前，研究具有时滞和脉冲的分数阶模糊惯性神经网络的渐近稳定性的论文较少.基于上述的工作,本文首先提出了一类新的具有脉冲效应的延迟分数阶模糊惯性神经网络，并将文[20]的主要结果从分数阶模糊神经网络推广到分数阶模糊惯性神经网络.其次，提供一些引理辅助主要结果证明.最后，利用压缩映射原理证明了系统(1)平衡点的存在唯一性．此外,通过构造合适的Lyapunov泛函,利用导出了Caputo分数阶算子与Riemann-Liouville分数阶算子之间的关系及其性质,以及分式Barbalat引理, 来研究系统(1)的渐近稳定性.

1 预备知识和引理

本节将介绍一些关于Caputo和Riemann-Liouville分数阶微积分的定义和引理.

定义1[21]函数x(t)的分数阶α>0的积分定义为

定义2[21]连续函数x(t)的Riemann-Liouville的α分数阶导数定义为

定义3[21]连续函数x(t)的Caputoα分数阶导数定义为

引理1[22]如果u,v∈C1[0,b],α>0,则

2)DαD-αu(t)=u(t)；

3)Dα(u(t)+v(t))=Dαu(t)+Dαv(t).

引理2[21]对于0<α<1,CDαx(t)=Dα(x(t)-x(0)).

引理3[15]如果x(t)∈R是连续,在[0,δ]上可导的,0

DpDqx(t)=Dp+qx(t).

引理4[15]如果x(t)∈R是连续,在[0,δ]上可导的,0

D-pDqx(t)=D-p+qx(t).

引理6[24]设x(t)与y(t)是系统(1)的两种状态变量,则有

2 主要结果

本节将研究Caputo分数阶模糊惯性神经网络(1)平衡点的存在性、唯一性和渐近稳定性, 给出本文的主要结果.

(3)

下面给出本文中要用到的假设条件：

(H1) 函数fj,gj(j=1,2,…,n) Lipschitz连续的，即存在正常数Fj,Gj使得，|fj(x)-fj(y)|≤Fj|x-y|,|gj(x)-gj(y)|≤Gj|x-y|,∀x,y∈R；

定理1 假设(H1)与(H2)成立.如果存在常数mi,pi(i=1,2,…,n)使得下式成立

(4)

则系统(1)有唯一的平衡点.

(5)

∀u=(u1,u2,…,un)T,v=(v1,v2,…,vn)T.

由条件(H1)及(H2),得到

进一步,由式(4)得到

从而‖Φ(u)-Φ(v)‖<‖u-v‖.即Φ是Rn上的收缩映射.故存在唯一的不动点u*使得Φ(u*)=u*,i.e.,

(6)

(7)

(8)

由(H3)得

CDβei(0)=CDβxi(0)=ψi(0)=0

(9)

故由式(8)和式(9)及引理1～引理3,有

CD2βei(t)=Dβ(CDβei(t)-CDβei(0))=Dβ(CDβei)(t)=

Dβ(Dβ(ei(t)-ei(0)))=Dβ(Dβei)(t)=D2βei(t)

(10)

其中0<β≤1.

通过式(10)可知系统(7)等价于以下系统

(11)

在式(11)中, 采用变量代换wi(t)=Dβei(t)+ei(t).由引理1与引理3, 有

Dβwi(t)=Dβ(Dβei(t)+ei(t))=D2βei(t)+Dβei(t).

于是系统(11)可以改写为

(12)

Dβei(t)=-ei(t)+wi(t),t≠tk,

定理2 设0<β≤1,条件(H1)～(H3)成立.如果选择适当的正参数mi与pi, 满足式(4)及下列不等式

(13)

mi+pi(1-ai)≤0,n=1,2,…,n

(14)

则系统(1)有唯一的渐近稳定的平衡点.

其中mi,pi是待定的正常数.当t≠tk时, 由引理1和引理4,计算V(t)的一阶导数，得

(15)

另一方面,当t=tk时,根据(H2),得到

因此,可以推断系统(1)是渐近稳定的.