多紧急等级复杂维修任务即时调度优化与应用

2021-11-30夔国凤赵越谢毅高小永潘军左信

化工进展 2021年11期

夔国凤，赵越，谢毅，高小永，潘军，左信

（1 中国石油大学(北京)自动化系，北京 102249；2 中国石油大学(北京)安全与海洋工程学院，北京 102249；3 北京万普隆能源技术有限公司，北京 100195）

油气田的高效稳定生产离不开许多昂贵的设备和设施，随着生产进程的推进，不可避免地会出现复杂多样的维修任务。油气设备和设施的管理与维护质量对油气企业的生产质量和效率影响很大，一定程度上提高了企业的运行成本[1]。对人力资源制定调度优化方案，合理地安排维修技术员前往井场进行维修，可以有效地减少故障引起的产量损失，降低生产成本。

调度优化的应用非常广泛，在聚氯乙烯[2-3]、医疗[4]、油气生产[5-6]等领域，已有大量的研究和应用。近年来，维修调度研究方面也逐渐有了许多报道，大致可以分为模型描述和优化算法两方面。在模型描述方面，通过综合分析战时维修调度问题，朱昱等建立了基于最大保障时间的维修任务静态调度模型[7]和考虑维修流程的多单元维修任务调度模型[8]。王正元等[9]提出了一种动态维修任务调度方法，先将原问题分为静态和动态问题，分别建立相应的数学模型，根据任务变化情况反复调用静态模型，实现战场抢修任务的动态调度。后来，他们还提出了一种考虑维修专业的动态维修任务调度方法[10]。吕学志等针对伴随修理和定点修理两种维修保障形式，分别提出了装备作战单元伴随修理的仿真模型[11]和用于评估维修任务调度策略的定点修理过程仿真模型[12]。Achkar 等[13]提出了油气井维修调度优化的基于离散时间的MILP 公式，解决了以最小化操作成本和生产损失为目标的维修人员调度问题。在优化算法方面，王浩[14]将蜂群算法引入装备维修任务调度研究中，仿真结果表明，蜂群算法对动态随机任务调度具有很强的优势。吕学志等[15]建立了考虑维修的维修任务调度混合整数规划模型，并提出了一种粒子群求解算法，实例证明了该算法的有效性。曾斌等[16]提出了一种基于退火进化的优化调度算法，实验证明该算法能在较快的收敛速度下提高保障单元的利用率。昝翔等[17]为了快速准确地获得装备维修的调度结果，采用一种改进最大-最小蚂蚁系统求解维修任务调度模型。针对陆上石油生产安排修井设备的调度优化问题，Aloise 等[18]提出了一种变领域搜索启发式算法。Ribeiro等[19]对修井机调度问题的三种元启发式算法进行了比较，其中自适应大邻域搜索算法的效果最佳。另外，也有一些非常优秀的综述。Nwadinobi等[20]对已发表的维修调度优化模型进行了调查总结和分类。陈春良等[21]在分析了装备维修任务调度的需求和意义后，对装备维修任务调度理论研究现状进行了综述。

综上所述，现有的维修调度研究主要集中在装备维修方面，对油气田生产设备的维修调度研究还很少，更没有考虑不同情况以及任务紧急程度的维修调度优化。本文分析了不同种类的维修任务后，提出了考虑不同情况的4种调度方案，包含定时调度、临时调度、手动调度及紧急调度。利用C语言编写调度软件并进行了应用验证，结果表明，所提出的调度方案可以实现对不同情况下维修任务的及时有效处理。

1 问题描述

传统的维修调度由人工完成，是定期派人去井场检查设备的运行状态，无论是否有故障发生，被派的维修人员必须按照指定的时间，挨个排查所分配的井口，这样就造成人力资源浪费，工具、设备利用率低，从而导致生产成本大幅提高，不利于公司生产。

维修调度包括：①建立详细全面的底层数据，如维修工具信息、人员技能信息、班次信息等，进一步建立人员信息、任务信息、日常排班信息等基础信息；②通过人为设定规则，计算机分析计算得出最优人员和任务匹配方案、最优路线，进行任务分配即人员调度；③手机端收到任务，查看任务所需工具、维修路线，根据任务操作提示、验收标准等进行维修，并最终反馈。在此过程中，前期基础数据的建立可能会消耗一定的时间，但是系统一旦建立，就可以解决传统巡井的盲目性，不再是按时间、按规定去巡井，而是按需求、按任务去巡井，大幅降低了人力资源，提高工具、设备利用率，从而降低生产成本，以达到提高生产效益的目的。

调度流程见图1。首先，从上位机系统中获取例如维修技术员、维修任务及维修井之间最短时间路径信息，即完成基础信息录入、维修任务读取模块任务，并将这些信息作为调度优化模型生成模块的输入信息。其次，生成维修任务调度优化的数学模型描述，结合求解器，对数学模型进行优化求解。最后，借助优化结果自动整理、分析与发布模块对优化求解结果实现分析、整理与回传数据库功能，经过调度员审阅后自动向维修员手机发布求解结果。若系统接收到突发情况的紧急任务申请，根据任务的紧急程度立刻或定时触发再调度操作。

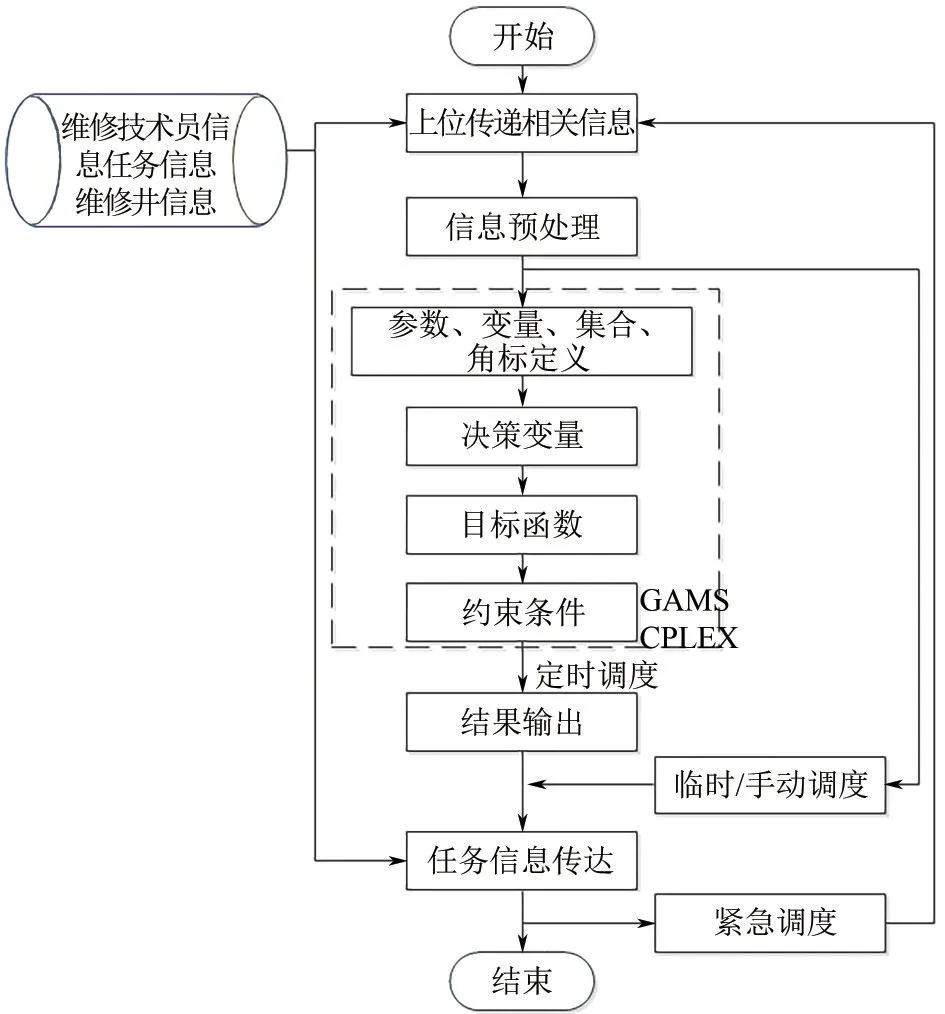
图1 调度流程

维修调度主要分为手动调度、系统调度和紧急调度。系统调度是指基于系统现有的数据基础，如任务信息、维修技术员信息、技能等级等基础信息，实现最少的车、最少的人，以最短的路径或时间进行的巡检任务分配。系统调度一般分为定时调度和临时调度两种情况。定时调度是指巡井开始前，由系统根据现有未调度任务情况和在值维修技术员情况，利用智能调度算法进行任务分配。定时调度每日调度时间固定，可根据不同时令自动区别，定时调度整体上要在巡井时间内进行任务分配。临时调度是指在巡井开始后，新添任务需要监控人员或者其他相关人员进行手动操作的系统调度。临时调度的调度时间不固定（一般情况在巡井时间内），需要充分考虑到维修技术员位置信息、任务完成情况、任务分配情况，更新指定维修技术员的任务列表。临时调度原则上在巡井时间范围内安排任务。

手动调度是指任务分派后，部分任务允许人为干预指定人员完成而进行的调度方式。手动调度需根据当前任务调度情况、维修技术员位置信息等相关约束，按照最优结果排序推荐，手动调度后，需要根据任务分配情况重新更新指定维修技术员的任务列表，原则上任务分配后时间不超过当日巡井时间。手动调度的任务需当日完成，任务为紧急时还需尽快安排。

紧急调度是指遇有突发情况，需要维修技术员尽快处理而产生的巡井任务。紧急调度时，结合维修技术员当前任务情况，自动推荐最佳的巡检人员。紧急调度后，自动更新维修技术员任务列表。紧急调度需要考虑紧急调度需求时维修人员处于工作、休息等情况。紧急调度流程见图2。

本文考虑上述4种调度方案，利用C语言编写了调度软件，结果表明，调度软件可以实现4种不同情况下的维修调度。

2 模型建立

针对不同的调度方案，本文建立了定时调度的MILP模型、临时调度和手动调度的MILP模型以及紧急调度模型。

2.1 定时调度的MILP模型

该部分建立的模型是由系统根据现有未调度任务的情况和在值维修技术员情况进行的任务分配模型。该模型考虑了维修任务类型的多样性、维修技术员的技能水平和工作时间范围、维修任务所处的物理位置、多维修任务在调度时间点并发产生等约束限制，以期在尽可能短的时间内完成最多的维修任务量，且维修技术员的行驶时间最短，最终决策出维修任务分配情况和执行顺序，确定每个维修任务的开始和结束时间。

2.1.1 问题假设

所建立的模型需要满足以下假设条件：①一个任务只需要一个维修技术员完成，各维修技术员独立完成各自分配到的维修任务，且维修任务相互独立，不存在相互支援的情况；②维修任务所在井、各维修技术员完成维修任务的时间、任务的重要度优先级、任务的技能等级需求、维修员技能等级等相关信息均已知；③任务之间相互独立，没有从属关系；④仅考虑维修任务是否在维修技术员的修理能力范围内，不考虑需要的设备器件等是否短缺；⑤前往任务所在位置均使用相同的交通工具且匀速行驶；⑥同一井存在多个维修任务，且任务的重要度由优先等级进行划分，同井的任务优先级不唯一。

2.1.2 MILP模型

（1）时间顺序约束定义每位维修技术员时间轴上时间段的始末时间的先后关系。对于每位维修技术员，下一个事件点的开始时间必须滞后于前一个事件点的结束时间，见式(1)。且均不能超过调度周期范围，见式(2)与式(3)。

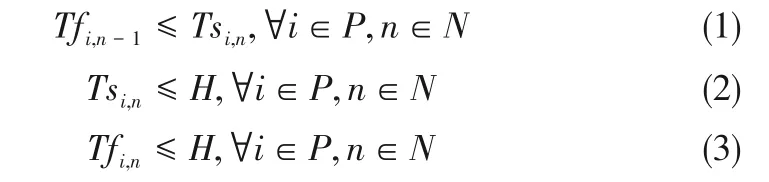
（2）事件点持续时间约束每个时间段的时间长度由该时间段归属的维修技术员和处理的维修任务确定，见式(4)和式(5)。

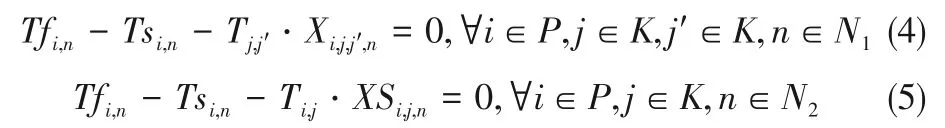
（3）任务分配约束一个任务最多只能完成一次，见式(6)。每位维修员的每个时间段最多只能安排一个任务，见式(7)。优先级为1和2的任务必须被安排，见式(8)。

（4）事件与时间段匹配约束前文提到，事件包含任务进行中和任务转换中两种类型，两种类型任务在时间轴上是交替出现的，因此同一时间轴的相邻时间段XSi,j,n和Xi,j,j′,n的取值只能是{0,1}或{1,0}。式(9)和式(10)保证了该规则，但由于两式是两个离散变量的乘积形式的非线性多项式，根据You 和Grossmann[22]提供的线性化思想，将这两式线性化为式(11)～式(15)。

（5）中断任务约束保证每位维修技术员在中午休息时间回到维修中心站，休息结束后继续完成剩下任务。式(16)保证每位维修员会分配到一个时间段休息，式(17)和式(18)确定休息时间的开始和结束时刻。由于式(17)和式(18)是属于离散变量和连续变量乘积形式的非线性多项式，参考You 和Grossmann[22]提供的规则可依次线性化为式(19)～式(23)和式(24)～式(28)。

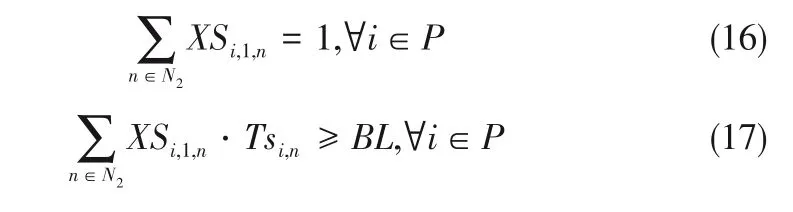
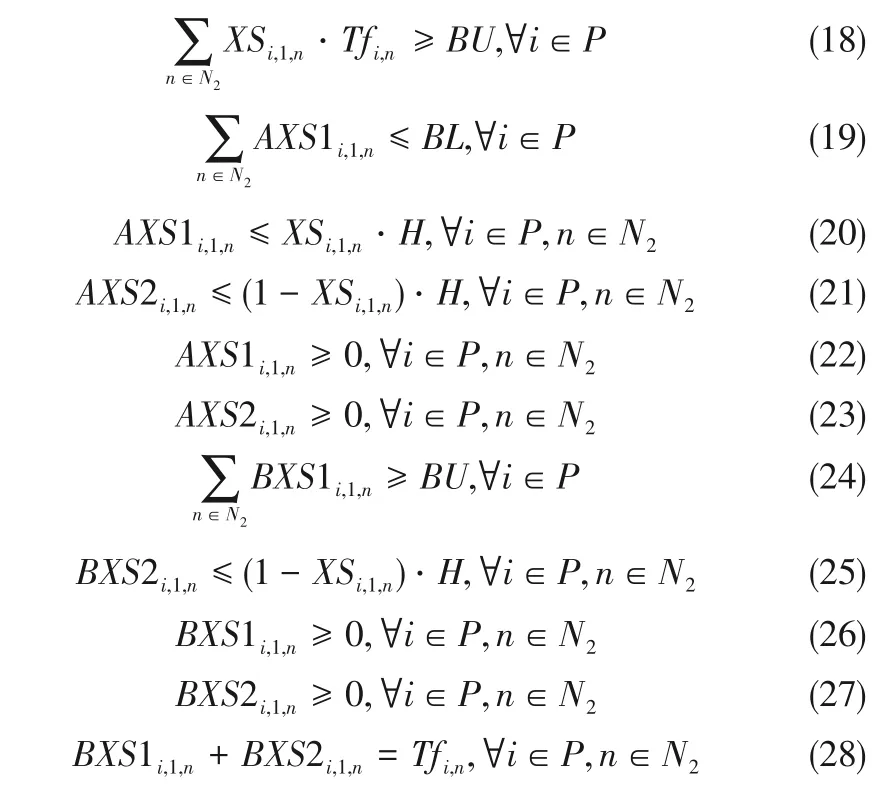
式(29)为该模型的目标函数，最小化成本和最大化任务量。为了描述方便，均统一为时间表示的成本问题。最终的目标函数包含四部分信息，第一项是一个软约束，即在每个技术人员的任务列表中优先级为1 的任务必须优先完成，M1是优先级惩罚的时间归一化系数；第二项是最大化安排任务数量，即在满足约束条件的前提下，尽可能多地安排维修任务，M2表示任务量归一化时间系数；第三项是最小化所有技术人员的路途行驶时间，M3确定总路途行驶时间的成本系数；第四项也是一个软约束，即保证在任务量较少的情况下，尽可能早地结束维修工作，M4是该项的时间归一化系数。

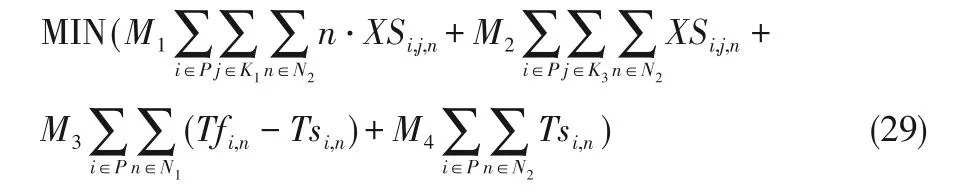
2.2 临时调度和手动调度MILP模型

临时调度是新添任务需要监控人员或者其他相关的人员进行安排；手动调度是任务分派之后，部分任务需要人为干预指定人员完成。所以，临时调度模型和手动调度模型可以归纳为同一个数学模型，但是输入参数不同。

2.2.1 问题假设

假设条件与定时调度相同。

2.2.2 MILP模型

调度专家根据现场的经验以及原始数据的分析，对式(29)目标函数中的系数M1、M2、M3、M4进行赋值。接下来详细介绍系数M1、M2、M3、M4的赋值过程。

根据式(8)，优先级为1 和2 的任务必须被安排。目标函数第一项为在每个技术人员的任务列表中优先级为1的任务必须优先完成。为了达到目标函数的最小化，n也会取到尽可能小的值，来保证优先级为1的任务优先完成。目标函数第二项是最大化安排一般任务数量，即在满足约束条件的前提下，尽可能多地安排一般任务。如果在优先级为1和2的任务被安排之后，调度周期内剩余时间不足以完成任何一个一般任务，此时第二项将不存在任何意义；如果在优先级为1 和2 的任务被安排之后，调度周期内剩余时间可以完成一般任务，此时为了保证时间的紧凑性，设置M1=M2=M，M为任意大于0的值。

在保证优先级为1的任务优先完成并且最大化完成一般任务量的前提下，目标函数中还设置了第三项与第四项。即同时保证最小化所有技术人员的路途行驶时间；而且保证在任务量较少的情况下尽可能早地结束维修工作，因此设置M3=M4=m，m为任意大于0的值。

M1、M2、M3、M4的取值主要包括三种情形，分别描述如下。

情形1：

最初的维修任务列表包含紧急任务、重要任务、一般任务时，系数M1、M2、M3、M4的取值见式(30)。

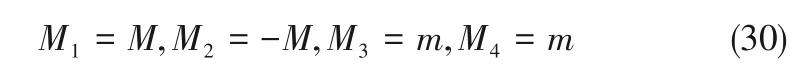
此时调度模型最主要的是满足优先级为1的任务优先完成，一般任务尽可能多完成。同时，保证最小化所有技术人员的路途行驶时间并尽可能早地结束维修工作。

情形2：

最初的维修任务列表包含紧急任务、重要任务时，系数M1、M2、M3、M4的取值见式(31)。

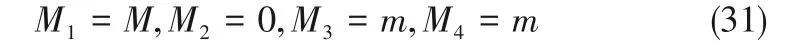
此时调度模型最主要的是满足优先级为1的任务优先完成。同时，保证最小化所有技术人员的路途行驶时间并尽可能早地结束维修工作。

情形3：

最初的维修任务列表包含重要任务、一般任务时，系数M1、M2、M3、M4的取值见式(32)。

此时调度模型最主要的是满足一般任务尽可能最多完成。同时，保证最小化所有技术人员的路途行驶时间并尽可能早地结束维修工作。

2.3 紧急调度模型

紧急调度部分没有具体的数学模型，该部分主要是对数据预处理和预判断。

时间约束的优化处理与预判断。

（1）如果所有紧急任务和重要任务的时间总和超过维修工时，则调度肯定无解，此种情况下以完成任务量最大为目标进行调度（既然完成任务量最大化，则路径自然应该是最优，只有充分节约了井组间运动时间才可完成任务数最大化）。

（2）如果紧急任务和重要任务时间总和少于维修工时，则可能存在调度优化解，此时启动正常优化求解（即在模型中以约束形式强制要求所有紧急和重要任务必须完成）。

紧急调度判断与处理。

（1）如果非工作时间内出现紧急任务，则以时间最优为目标进行优化。

（2）如果工作时间内出现紧急任务，分上午和下午两种情况进行优化求解：如果上午出现紧急调度，则模型中考虑维修技术员的中午午休约束；如果下午出现紧急调度，则模型中无需考虑午休约束问题。

3 仿真案例

建立了定时调度MILP 模型、临时调度和手动调度MILP 模型以及紧急调度模型后，利用C 语言编写了调度软件。3.1 节中对定时调度案例结果做了详细说明，3.2 节是四种调度方案的仿真案例的结果汇总。

3.1 定时调度

3.1.1 测试用例

假定有维修技术员4 人，2 人为高级技术员，2人为中级技术员；一共有待维修任务74个，其中重要任务23 个，一般任务49 个，紧急任务2 个。在本例中通过大量的案例数据总结分析，在统计意义下给出一组相对合理、求解可靠的经验值：M1=M2=M=10，M3=M4=m=0.01。调度结果见表1～表4。

表1～表4中，各个时间表中标红色的为紧急任务、标橙色的为重要任务、标绿色的为午休、其他的则为一般任务。4位维修技术员（分别为951号、311 号、767 号和050 号）的调度结果甘特图见图3。图3 中每个方框内的数字表示每一位维修技术员所维修的任务以及所花费的时间，例如ID 为951 的维修技术员第一个维修的任务编号为1171，花费41min。

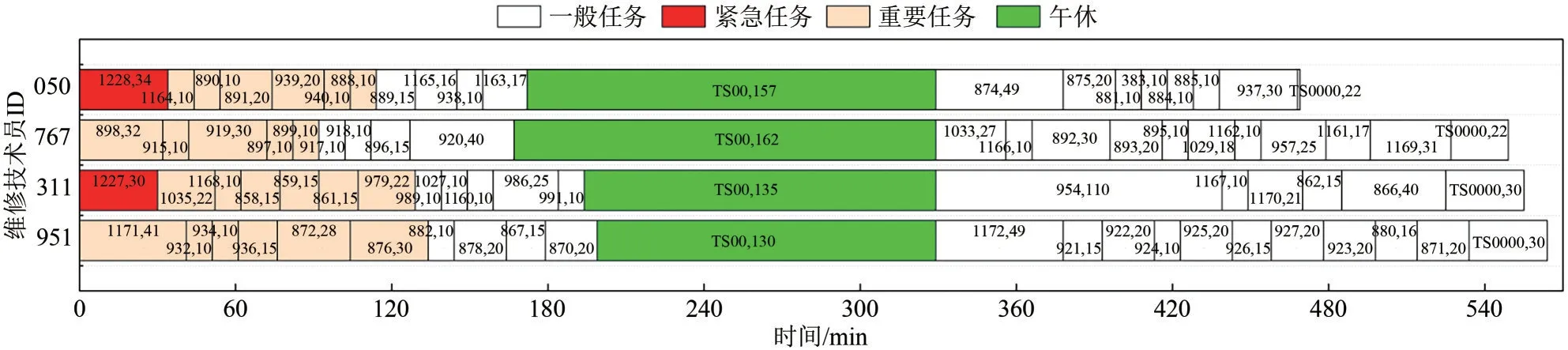
图3 定时调度甘特图

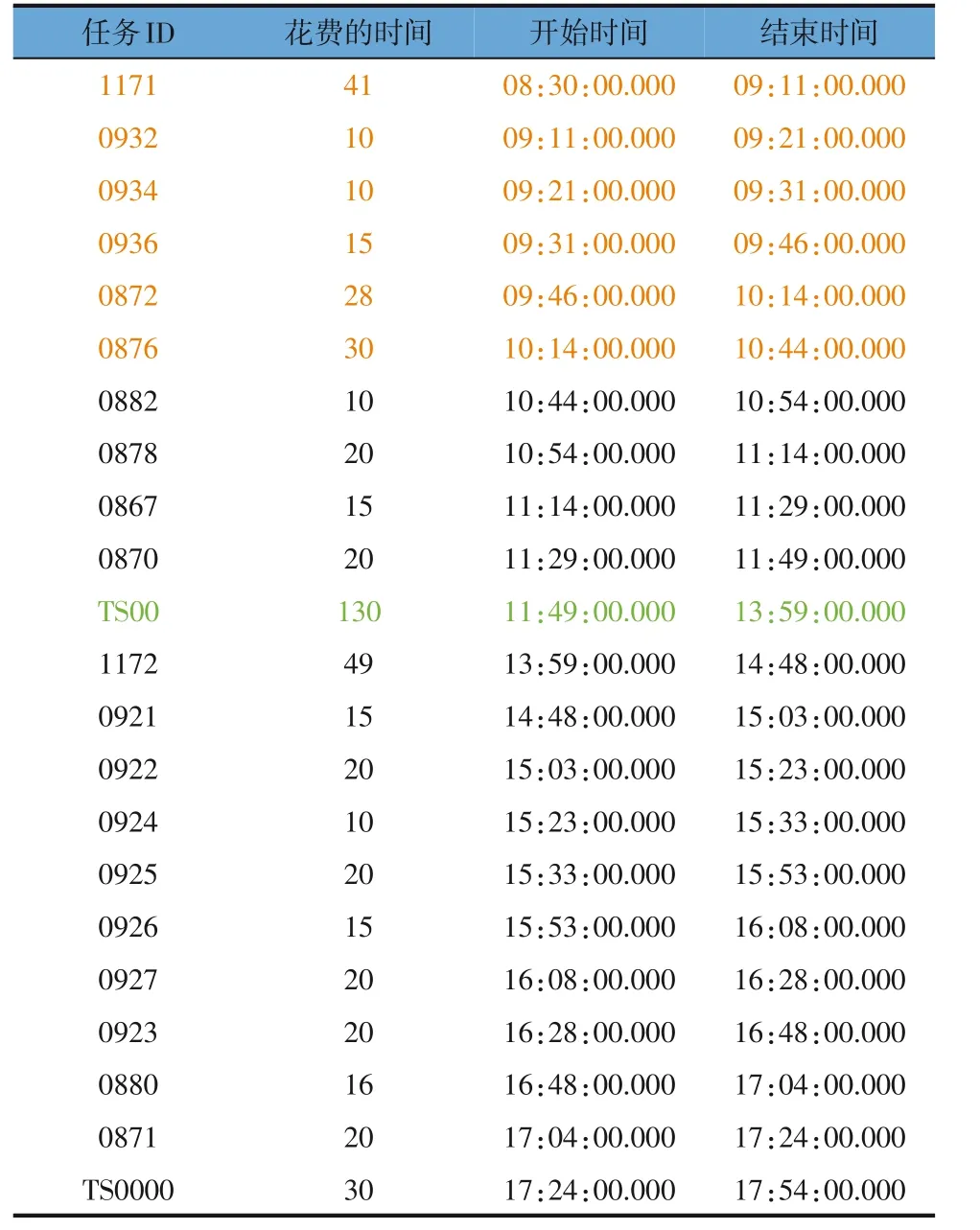
表1 951号维修技术员时间表

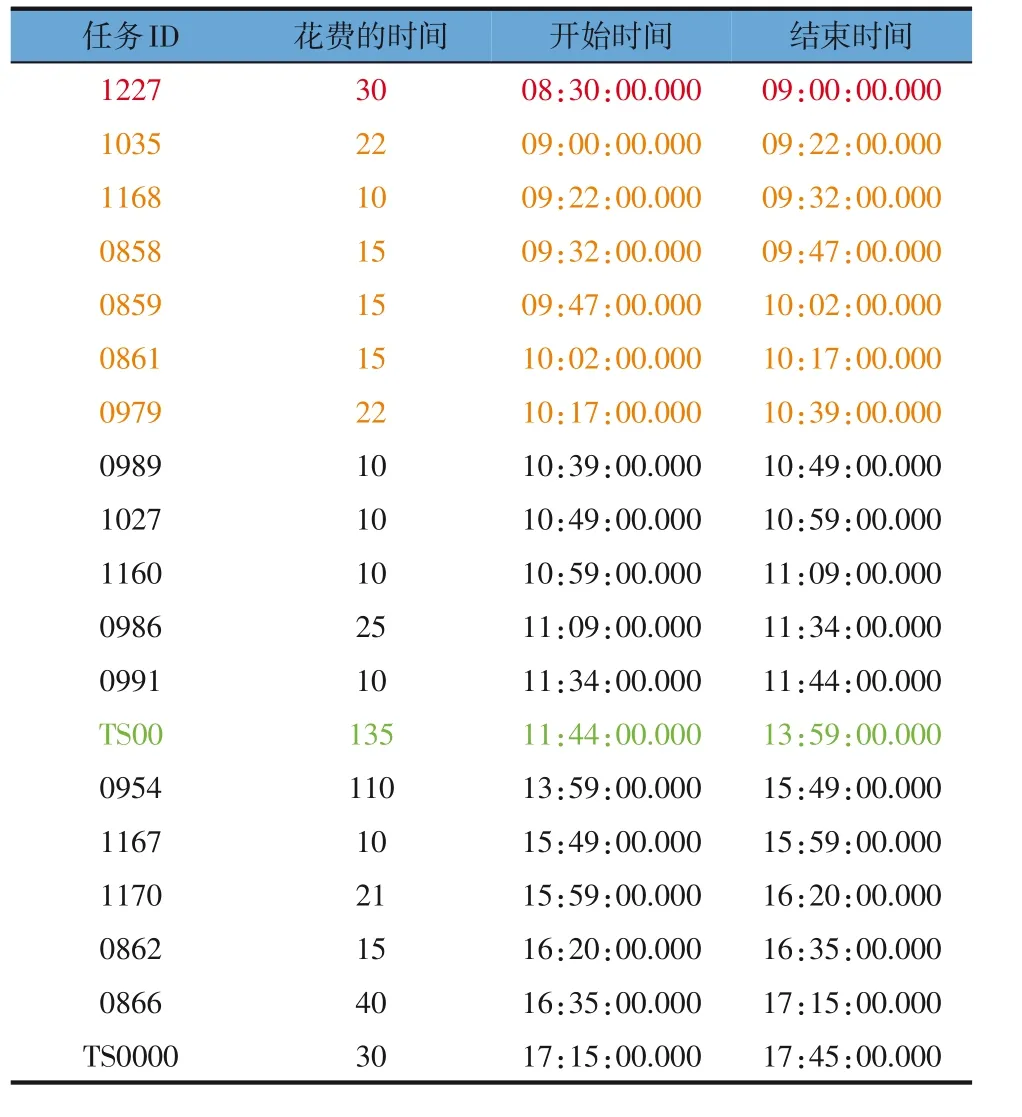
表2 311号维修技术员时间表

表3 767号维修技术员时间表

结合表1～表4 可以看出，4位维修技术员均在早上8:30出发，完成一天的维修工作后，在晚上18:00 之前回到维修站（TS0000）。中午12:00—14:00在维修站休息。两个紧急任务1227 和1228 均被完成。调度结果表明，本文中所提出的调度方案合理有效。

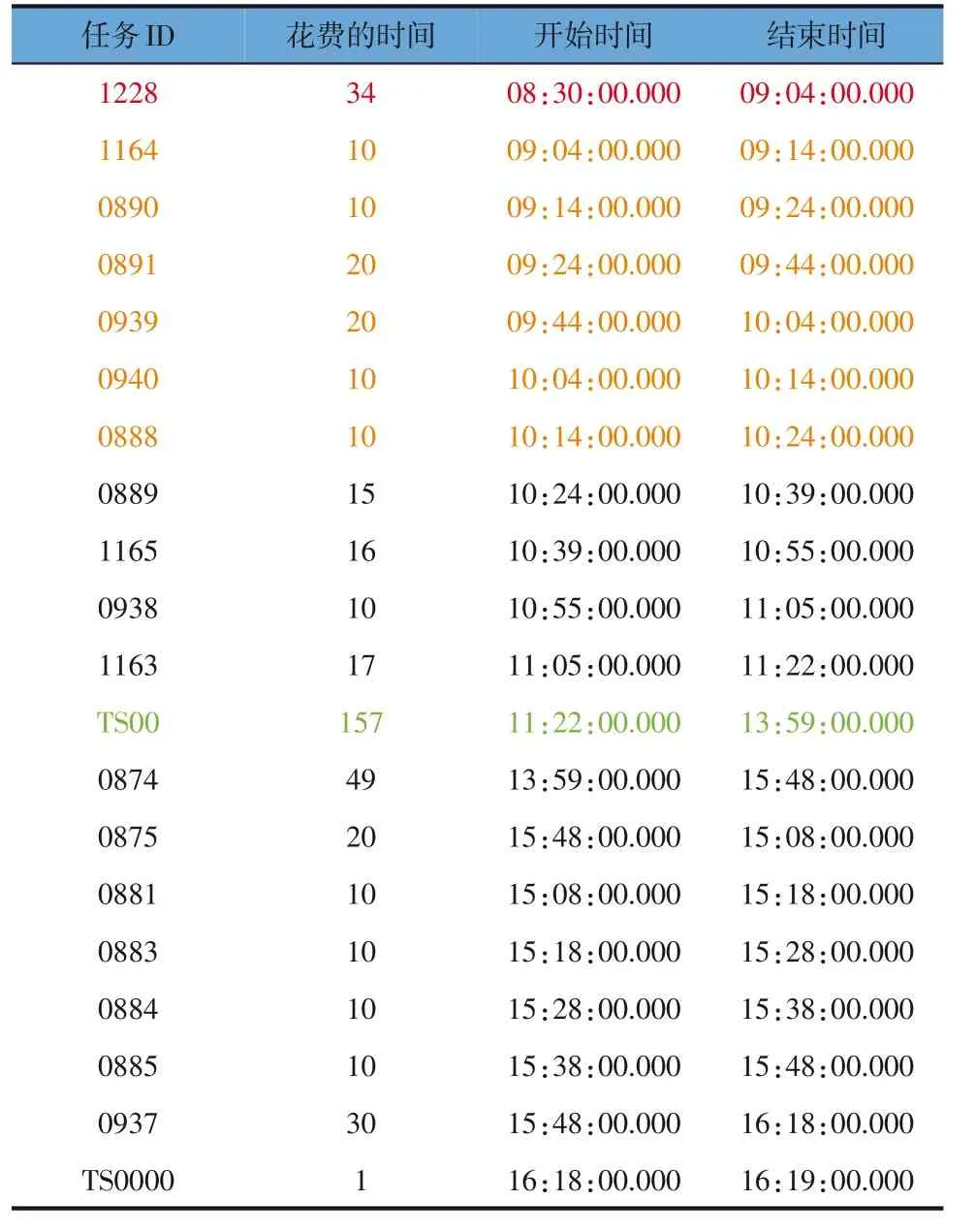
表4 050号维修技术员时间表

3.1.2 测试结果

（1）任务安排饱满：四个人任务均安排饱满，共计做了74 个任务（已去除早上从维修站出发以及傍晚回维修站任务），四人分别所做任务数为20、17、19、18。

（2）紧急任务、重要任务均已完成（紧急任务1227、1228均已按照优先级安排）。

（3）所要求的任务做了74 个，时间饱满，结果合理有效。

3.2 仿真结果

在本节中，对4种调度方案对应的仿真实验的结果进行了统计，结果见表5。

需要说明的是，在临时调度时，设置临时任务出现在9:30；在手动调度时，需要指定待维修的任务和待安排的维修技术员；在紧急调度时，设置紧急任务出现的时间为10:30，即需要考虑中午休息的约束。

从表5 的结果可以看出，在4 种调度方案中，优先级为1 和2 的任务，即紧急任务和重要任务，在调度周期内，都安排了维修技术员前往处理。目标函数第三项为最大化完成一般任务的数量，因此临时调度案例中的49 个待维修一般任务只完成了48 个。具体求解时间与人员、任务数量以及求解器性能息息相关。针对本文中给出的不同案例，优化求解收敛时间如表5所示。此外，目前大量运行案例的统计数据表明，调度优化求解时间为分钟级。