循环射流混合槽内液液两相混合特性数值模拟

2021-11-30孟辉波刘振江禹言芳张平吴剑华

化工进展 2021年11期

孟辉波，刘振江，禹言芳，张平，吴剑华

（1 沈阳化工大学机械与动力工程学院，辽宁沈阳 110142；2 沈阳化工大学辽宁省高效化工混合技术重点实验室，辽宁沈阳 110142）

混合是化工过程中最重要的组成部分之一，在许多工业反应中起着重要的作用[1-4]。化工生产过程中主要的液-液混合设备有搅拌槽、静态混合器、高剪切混合器、超重力反应器等。搅拌槽作为工业过程中的常见操作设备之一，可有效实现密度差异小的不互溶液液体系的分散过程[5-7]；静态混合器可有效克服密度差影响，改善局部过热，在受传递/混合速率控制的苯硝化等快速反应体系过程强化优势明显[8]；高剪切混合器由于具有局部较高的剪切速率和能量耗散速率，在液液乳化过程得到广泛的应用和研究[9]；超重力反应器在ms～s内实现分子级混合强化缩合反应，有效解决了高端化学品MDI 制造中混合难、副反应多、易堵塞停车等难题[10-11]。因此，液-液两相流的强化机理研究主要集中在分散相液滴粒径分布和流场流动特性等方面。李友凤等[12]对比分析了上述几种液液混合设备的强化机理及其不足。

循环射流混合槽是利用离心泵将高速流动的液体注入到静止或速度较慢的液体中，以实现快速混合。该设备具有造价低、能耗少、混合效率高及维修费用低等特点，可应用于各种化工过程[13-14]。Fossett和Prosser[15]采用实验的方法对单孔射流混合槽内的四乙基铅及石油的混合效果进行研究，得出混合时间关联式。Zughbi 等[16-18]对射流角度、射流高度、射流股数和对称性等参数对侧边三通、对边三通及单边三通等不同结构的射流混合槽的混合性能进行研究，发现侧边三通具有较好的混合效果。在射流槽中圆形喷嘴对射流的混合效果一直是研究的重点[19-22]，而对于异形喷嘴的混合效果研究较少。Mi等[23-24]用实验的方法对圆形、椭圆形、等边三角形、锐角等腰三角形和正方形等多种异形射流喷嘴进行研究，发现三角形喷嘴混合效果最佳。Azad等[25]与Quinn等[26]对尖角角度为10°、20°、30°和160°的三角形喷嘴进行实验研究，发现在射流近场区域角度越大射流卷吸特性越好。Eakarach等[27]对液体高度（H）与罐体直径（D）的比值以及对射流角度进行研究，发现液体高度与罐体直径对混合时间影响较小。Meng 等[28]对新型循环射流混合槽（CJT）内降液管结构进行研究，发现对称的矩形降液管能更好地减小射流中心线速度衰减趋势。Yu 等[29]通过数值模拟的方法对喷嘴间距、射流角度及挡板尺寸进行优化，并确定最合适的挡板尺寸及射流角度。禹言芳等[30-32]对CJT的湍流特性、瞬态压力脉动及喷嘴形状进行研究，发现CJT内喷嘴射流速度满足自相似性且能更好地实现混和。在上述射流研究中，侧重于研究单相流体，而在化工混合过程中，多为两种或多种物料的混合来实现工业目的。由于缺乏对其内多相体系流动和混合行为的研究，制约了循环射流混合反应器的优化设计与工业化应用。

本文选取水及二甲基硅油（C6H18OSi2）分别作为水相和离散相，在Re=3173～12692 和相含率αd=1.80%～6.00%条件下对循环射流混合槽内液液两相流动混合特性进行研究，分析量纲为1射流中心线速度、离析强度、拉伸率等参数的变化规律，以期为工业化推广提供理论依据。

1 数值模拟

1.1 物理模型

循环射流混合槽几何模型如图1所示，内部对称布置4块L形导流板，提升管、射流孔及降液管共同组成射流混合槽的流体循环部分。本文CJT计算模型直径为0.4m，槽体高度为0.4m，混合槽其余部分的结构参数见文献[28]。流体流动和混合是影响化学反应的重要因素，离析指数是表征流体混合程度的常用参数。为了避免射流孔等湍流强烈区域对宏观混合时间计算的影响，在混合槽液面以下区域采用图1 所示的1 个直径尺度的圆柱与4 个对称球两种方式Patch二甲基硅油。

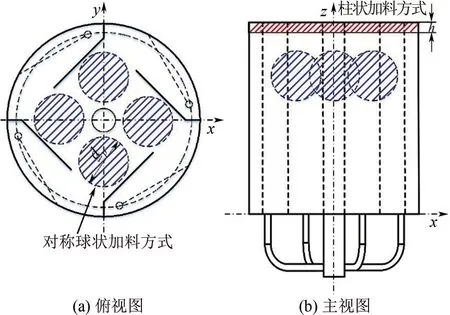
图1 CJT的几何模型及Patch位置

计算工质温度为20℃，以水为连续相：密度为998kg/m3，黏度为1.003×10-3Pa·s；二甲基硅油为分散相：密度为1000kg/m3，黏度为0.02Pa·s。分散相的两种Patch 方式、区域大小和注入位置详见表1。

表1 Patch参数

1.2 数值模型与方法

第k相的连续性方程和动量方程如式(1)～式(3)[33]。

连续性方程

动量方程

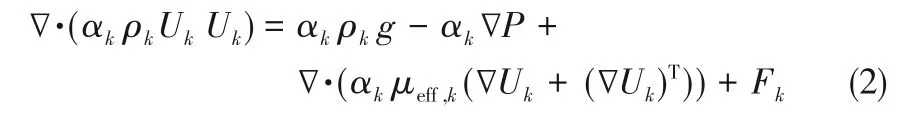
式中，αk为相体积分数；ρk为相密度；Uk为相矢量速度；g为重力加速度矢量；Fk为相界面合力；P为压力；μeff,k为有效黏度。连续相的有效黏度中包含连续相分子黏度μc和湍流黏度μt两种，即μeff,k=μc+μt。

利用CFD ANSYS Fluent V16.1软件进行三维非定常不可压缩的N-S计算；根据多相流模型的适用条件，选取Eulerian-Eulerian 模型[34-36]。Yu 等[29]在模拟中采用SSTk-ω模型对循环射流槽进行研究且通过与其他模型相比，发现SSTk-ω模型能更好地反映流场中的流动信息；Hosseini等[37]发现SSTk-ω模型更适合于强剪切流的复杂结构三维流动；Meng 等[28]采用LES、Standardk-ε、RNGk-ε和SSTk-ω模型对循环射流混合槽内流动及混合特性进行研究，SSTk-ω模型与实验结果[14]有着很好的一致性。

本文选用SSTk-ω模型，k和ω方程如式(4)～式(6)[33]。

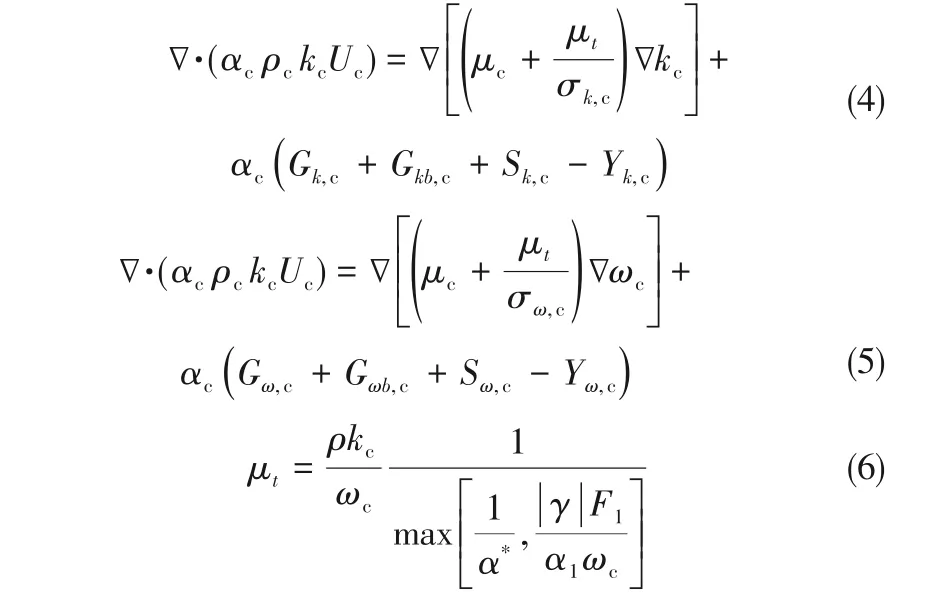
式中，F1为闭合系数；其余参数见文献[37]。

1.3 边界条件

为实现CJT内流体循环流动，在提升管下方加入动量源，混合槽壁面采用无滑移边界条件。采取Phase Coupled SIMPLE 对压力速度耦合进行数值计算，动量方程、湍动能方程、耗散率方程均采用二阶迎风格式，梯度方程采用Least Squares Cell Based，在步长为0.005s 的计算条件下，残差收敛精度小于10-4。

本文在Q=1～4m3/h 下对不同Re进行计算，Re如式(7)所示，其中ρc、Q、μc、dj和N0分别为连续相密度、体积流量、连续相黏度、射流孔直径以及射流孔数目[28]。

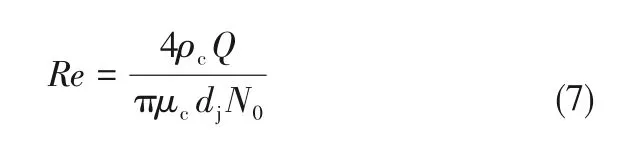
1.4 网格无关性

网格的疏密程度对数值计算的准确性和精确性有直接的影响，为提高计算精度，数值计算选用混合网格，4根射流管区域为结构化网格，导流板及其内部采用多面体网格。计算域网格如图2 所示，图2(a)为z/H=0.7时横截面网格分布，图2(b)为射流中心线截面网格图。采用160×104、247×104、326×104、401×104以及460×104五种不同数量的网格来进行网格无关性验证，对应的网格偏斜率QEAS分别为0.6908、0.6908、0.6836、0.6836 和0.7930。图3为t=28s 时不同网格数量下的量纲为1 射流中心线速度的比较，从图中可以得出，与460×104网格下的量纲为1射流中心线速度相比，网格数量为160×104、247×104、326×104、401×104下的量纲为1射流中心线速度的最大偏差分别为26%、27%、4.2%以及4.8%，由此可以看出网格数量为326×104以及401×104时与最大网格数量为460×104时计算结果具有较好一致性。因此，考虑到计算时间、网格偏斜率及计算精度3个关键因素，本文选取网格数量为326×104进行数值计算。

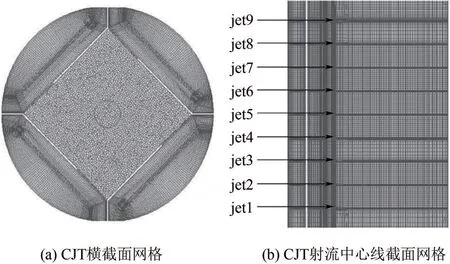
图2 循环射流混合槽不同位置处网格

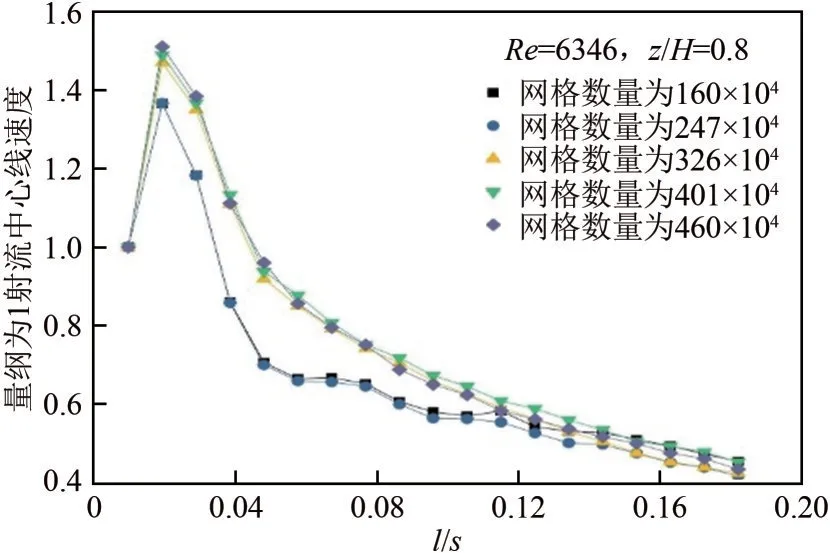
图3 不同网格数量下的量纲为1射流中心线速度

2 结果与讨论

2.1 射流混合时间

宏观混合有两个量化标准，即混合程度达到99%和95%。测量的混合时间是从示踪剂加入到达到95%混合时所用时间[38-41]。Al-Atabi[42]与Haddadi等[43]采用变异系数CoV[见式(8)]来对其混合程度进行衡量。

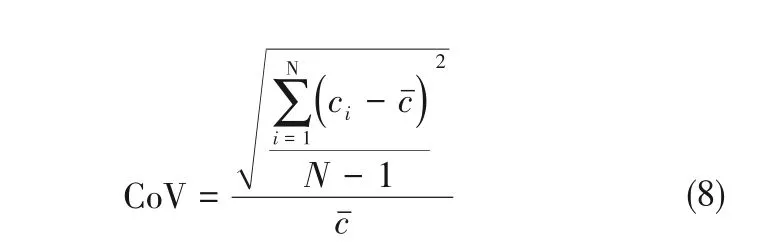
式中，ci为任意一点任意时间的瞬时浓度；是粒子平均浓度。本文选取混合程度达到95%时，即CoV=0.05时所耗费时间为混合时间。图4为CoV随混合时间变化规律，可以发现CoV随混合时间的增大而减小；在图4(a)中混合时间随相含率的增加而增大，在αd=1.80%、2.86%和6.00%条件下混合时间达到95%时，所耗时间分别为t=12.5s、13.0s和14.5s；图4(b)中混合时间随Re的增大而减小，在Re=3173、6346、9519 和12692 条件下混合时间达到95%时，所耗时间分别为t=21.5s、13.0s、9.0s和6.5s。因此本文选取t=28s 时计算结果进行数据分析。

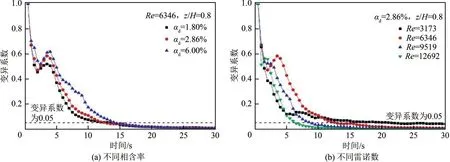
图4 变异系数随混合时间变化

2.2 射流中心线速度

射流中心线速度衰减越快，代表在射流阶段损耗能量越多，射流混合在卷吸环境下受阻越大。图5 为量纲为1 射流中心线速度（Um/Uo）变化规律。从图5(a)中可以看出，在l/s=0～0.08 时，不同相含率下的射流衰减速度下降迅速，并保持着良好的一致性。分散相相含率越高，所受的黏性力及阻力越大，因此在l/s=0.1～0.4时射流中心线速度衰减趋势缓慢，与αd=6.00% 相比，αd=1.80% 与αd=2.86%量纲为1 射流中心线速度衰减趋势分别减弱51%和21%。在l/s=0.4以后为射流后期阶段，多股射流之间的掺混与卷吸效果的影响使其衰减速度较慢。

图5(b)为同一相含率不同雷诺数下的Um/U0变化规律，可以看出射流中心线速度衰减趋势相同，在l/s=0.0～0.3 阶段时，量纲为1 射流中心线速度急速衰减。与Re=3173相比，Re=6346、9519和12692时量纲为1 射流中心线速度衰减趋势减弱2.60%、2.87%以及12.69%。但随着l/s的增大，四种不同雷诺数下的量纲为1射流中心线速度受多股射流之间掺混的影响，呈现出一种缓慢衰减的趋势。

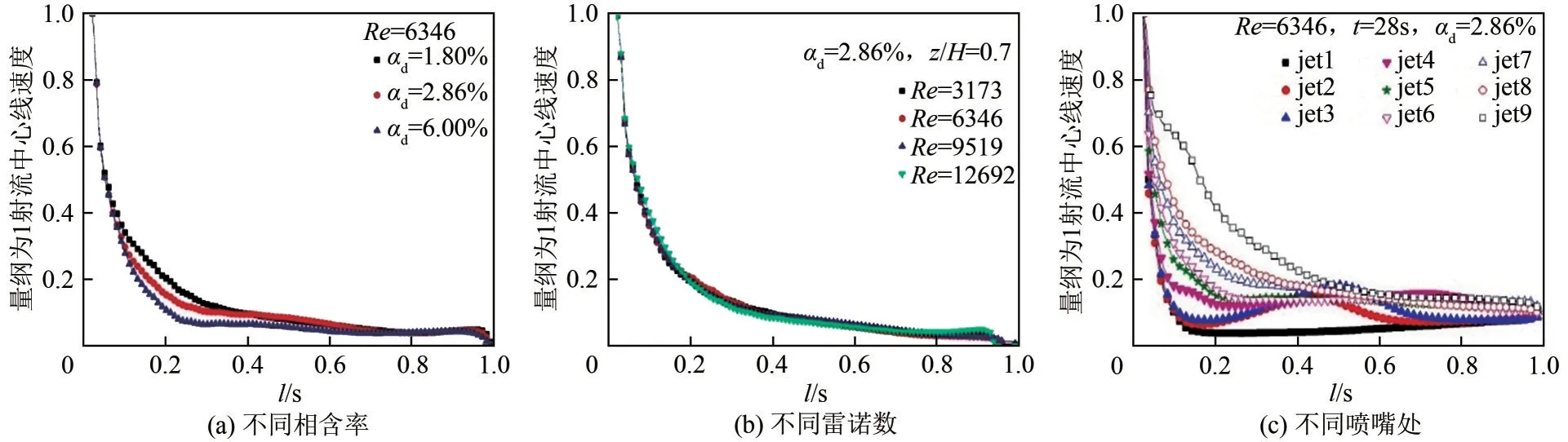
图5 量纲为1射流中心线速度变化规律

图5(c)为不同喷嘴下的Um/U0变化规律。Um/U0随l/s增大呈下降趋势；jet1在l/s＞0.1时流动方向受升力和卷吸效应的影响发生改变，使Um/U0＜0；jet2与jet3 在l/s=0.15～0.45 范围内随l/s的增大卷吸效应增强，Um/U0流动方向发生改变；在较高位置处的jet6～jet9喷嘴受升力和卷吸的耦合效应较弱，导致jet6～jet9喷嘴处射流中心线速度衰减趋势减缓。

2.3 离析强度

为衡量两相混合物的混合过程，Danckwerts[44-45]和王宇良[46]采用离析强度（Is）分析液体、粉末和气体的混合效果。Is的计算如式(9)。

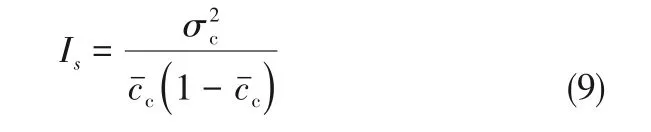
图6为CJT 内不同截面位置处的速度流线图和等值线图。从图6(a)可以看出，受初始高速射流的影响，在射流中心线两侧形成4组旋转方向相反的径向二次流涡对（counter-rotating vortex pair，CVP）；受降液管壁面的影响，在降液管中心形成强制涡，且越靠近中心位置处速度越小。图6(b)为不同角度下的速度流线图，在θ＜60°时受CJT 上下两壁面及拦液板导流的作用，在主流区域形成两对方向相反的周向强制涡对，但随θ增大周截面内的涡缓慢消失；在θ＞60°时射流区域流线与主体区域流线趋于一致，形成轴向流型。图7为射流孔处速度等值线图，受升力和卷吸效应的影响，在jet1～jet4喷嘴位置处射流中心线往上偏移，在jet1与CJT 底面形成强制涡，射流中心线速度方向相反且中心速度低，这与图5(c)中规律一致。

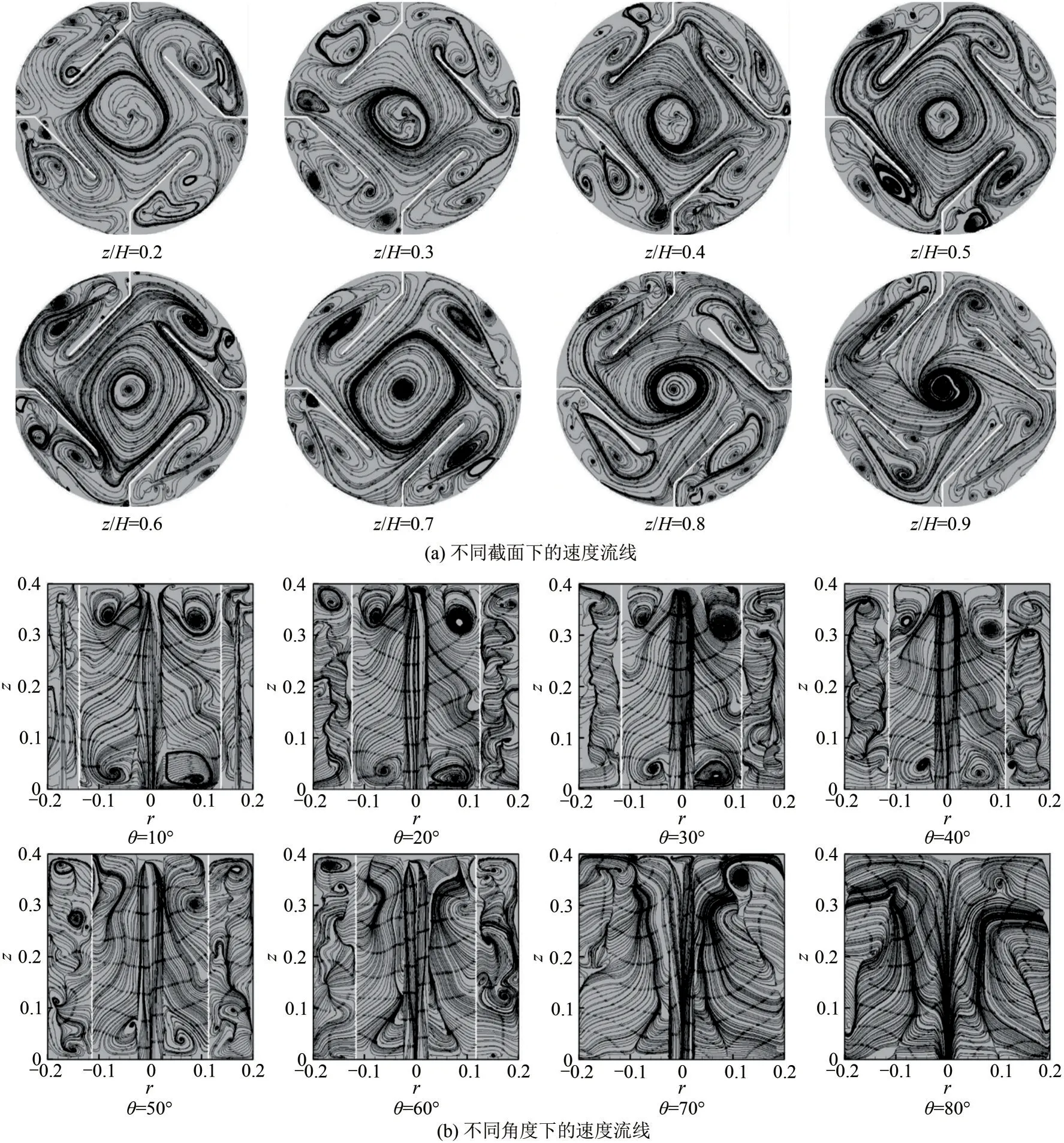
图6 不同位置处的速度流线及等值线

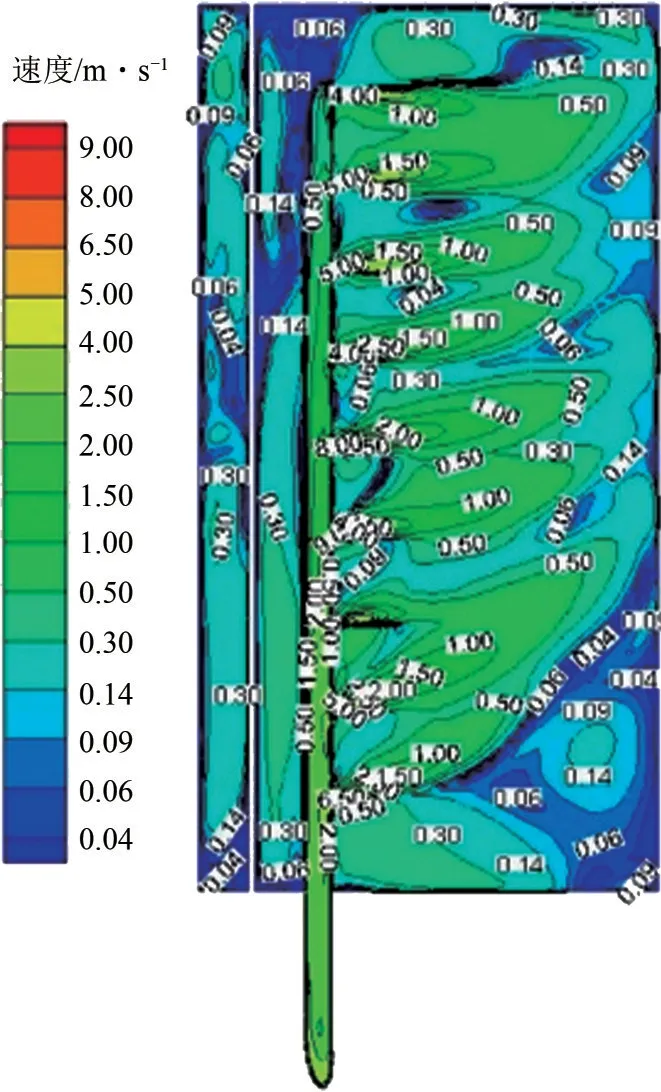
图7 射流孔处速度等值线图

Is=1 表示两种液体未发生混合；Is=0 表示达到完全混合。离析强度的变化规律见图8。从图8(a)中可以看出，离析强度Is随混合时间t的增大呈现减小的趋势。t=18s时Is为0.0044，且随着t的增大，相较于t=21s 时的Is最大变化率为0.32%，且在28s后的变化率已经变为0.01%，因此判定其达到完全混合。

图8(b)为不同截面的离析强度。从图中可以看出不同截面位置时混合十分均匀，且Is随着z/H基本上没有变化，各个截面的混合效果符合在图8(a)中提出在28s 时的混合均匀；在z/H=0.95 时卷吸及掺混效应对该截面影响小，对流扩散作用较其他截面弱，导致此处分散相浓度高，离析强度大，与z/H=0.9 相比，z/H=0.95 时离析强度增大4.1×10-5。从图8(c)中可以看出离析强度Is随θ的增大呈W 形趋势，结合图6分析发现，在射流中心线两侧形成反向涡对，流体停留时间增大，导致其离析强度在θ=10°～40°时较高。

图8(d)揭示了r/R对离析强度的影响，在降液管内离析强度较高，降液管外离析强度呈平稳趋势，且Is在10-5波动。根据流体动力学分析，图8(d)中降液管中心形成强制涡，使得分散相液滴发生聚并，导致在r/R=0～0.12 内离析强度高；在r/R=0.125～0.75时涡流扩散及对流扩散的作用使其分散相相含率分布均匀，在此区域内离析强度低；在r/R=0.75～0.85时由于射流中心线两侧的反向对涡使得流体停留时间增大，离析强度高。

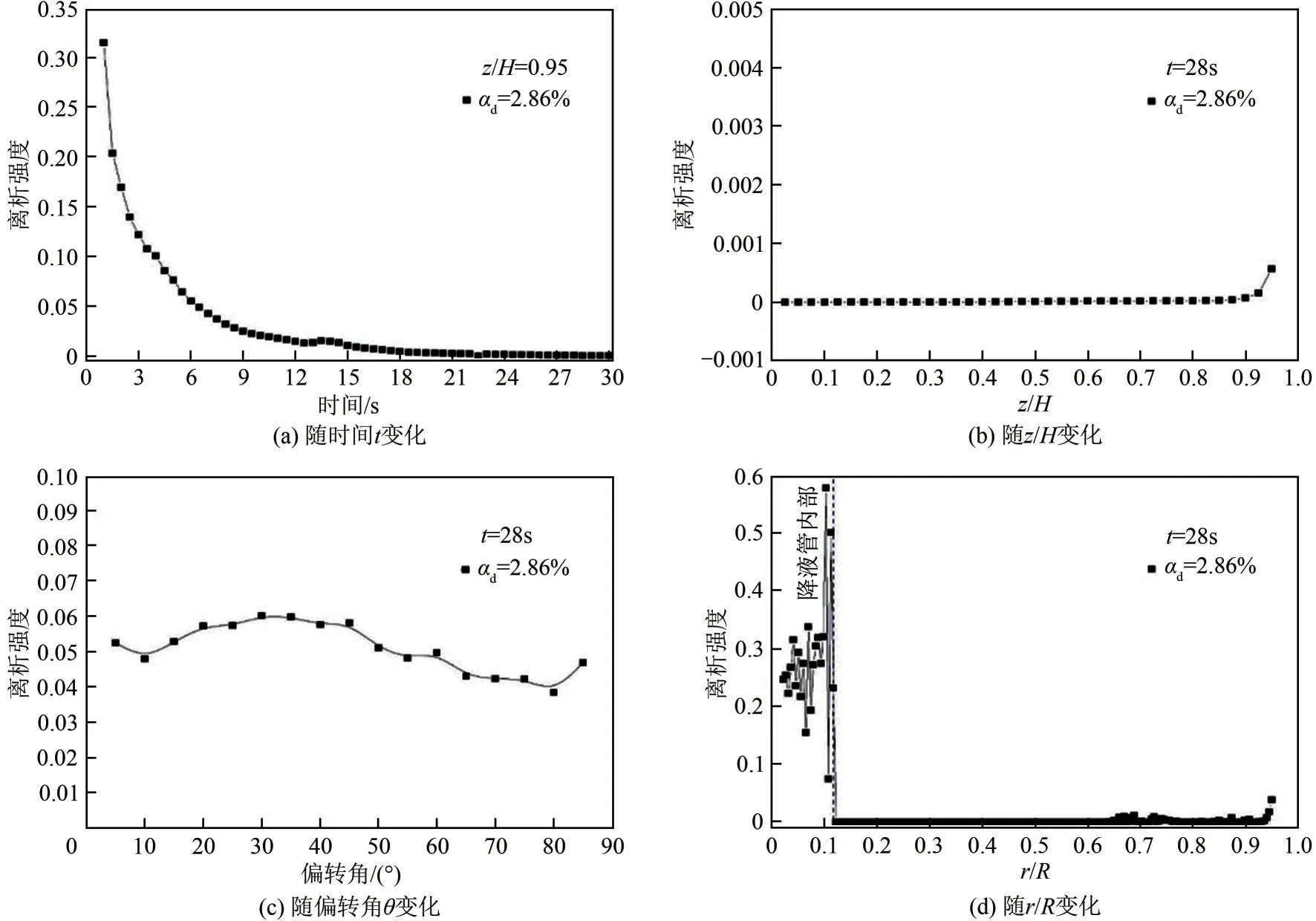
图8 离析强度变化规律（Re=6346；z=388.56～400mm）

2.4 加料方式

图9为不同加料方式下CJT 内流体的混合及流动的影响。从图9(a)看出，柱状与对称球状加料方式下的离析强度随时间的增大呈下降趋势，柱状加料方式下的离析强度在t=14.5s 后离析强度最大变化率为4.46%，因此判定t=14.5s 时已达到完全混合；对称球状加料方式下的离析强度在t=5s后离析强度最大变化率为5.71%，因此判定t=5s时对称球状已达到完全混合。由此可以发现，与柱状加料方式相比，对称球状加料方式达到稳定时的混合时间减少65.5%。

图9(b)为不同加料方式下的量纲为1 射流中心线速度。从图中可以看出，两种加料方式下的速度衰减趋势一致，由于受到流动阻力及相间作用力的影响，导致在l/s=0～0.3时射流初始阶段速度衰减趋势较大，而在l/s=0.3以后因为受到掺混与卷吸效应的影响呈现出缓慢下降的趋势。与柱状加料方式相比，在l/s=0～0.38 范围内对称球状加料方式下的射流中心线速度衰减趋势减弱14.2%。

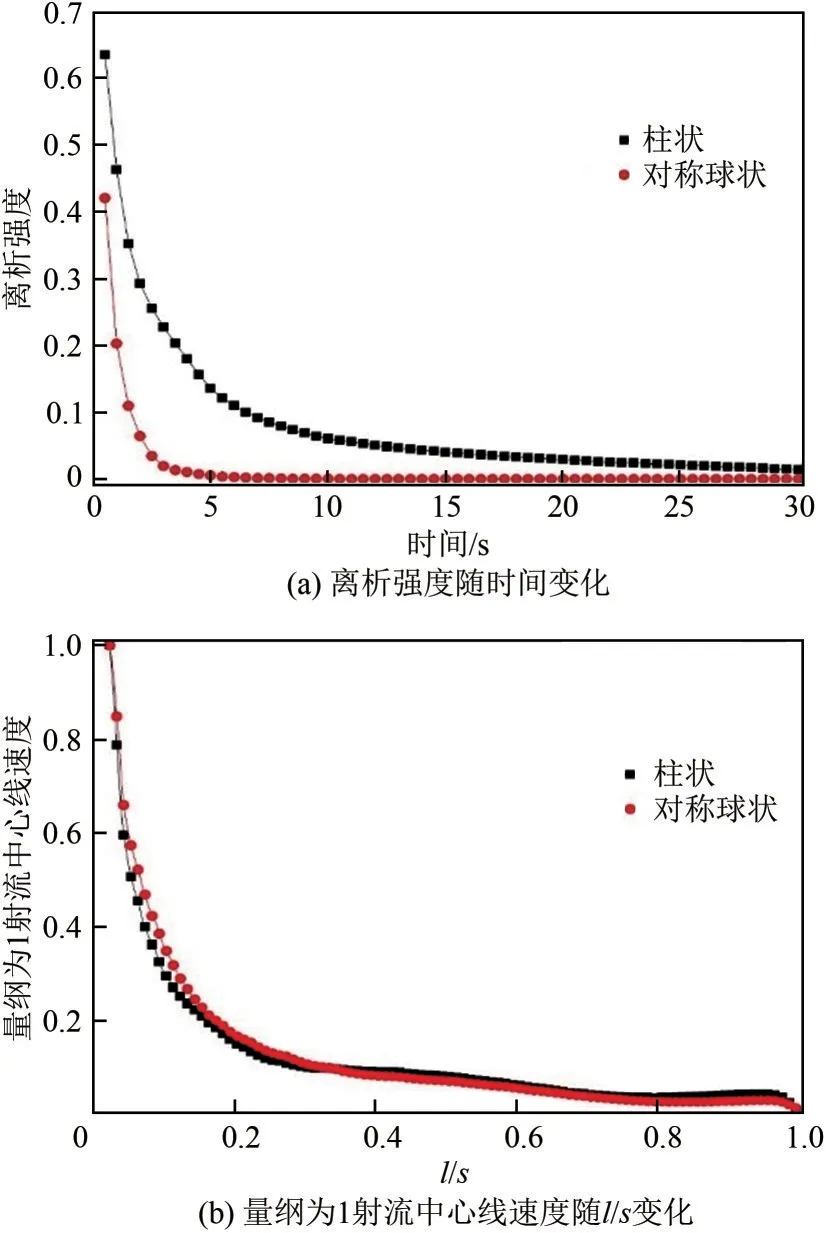
图9 不同加料方式对混合与流动的影响（Re=6346；z/H=0.5；αd=2.86%）

2.5 拉伸率

Ottino[47]采用物质元素的条纹拉伸和折叠对混合器进行混沌分析。拉伸率决定微混合过程的速率，可以通过增加材料间的区域和减少所需的扩散距离来实现组分的相互扩散。Meng 等[48]对不同插件的静态混合器进行研究，通过将一个物质点放置在一个任意的初始位置，当它通过静态混合器管道时，通过跟踪附着在该点上的向量来计算拉伸率，并且物质点经历高（低）拉伸的位置对应于良好（较差）混合的区域。采用相同方法，通过追踪无质量粒子的轨迹计算拉伸率来研究CJT内微观混合特性。

图10 为从jet5 喷射出的无质量粒子簇的轨迹图，粒子经高速射流后从射流区到中心混合区域，沿降液管到动量源，随后经过提升管从其他喷嘴位置处喷射而出形成循环，粒子轨迹占据整个流体域，随混合时间的增加，在t=10.11s时粒子轨迹充满整个流体域。

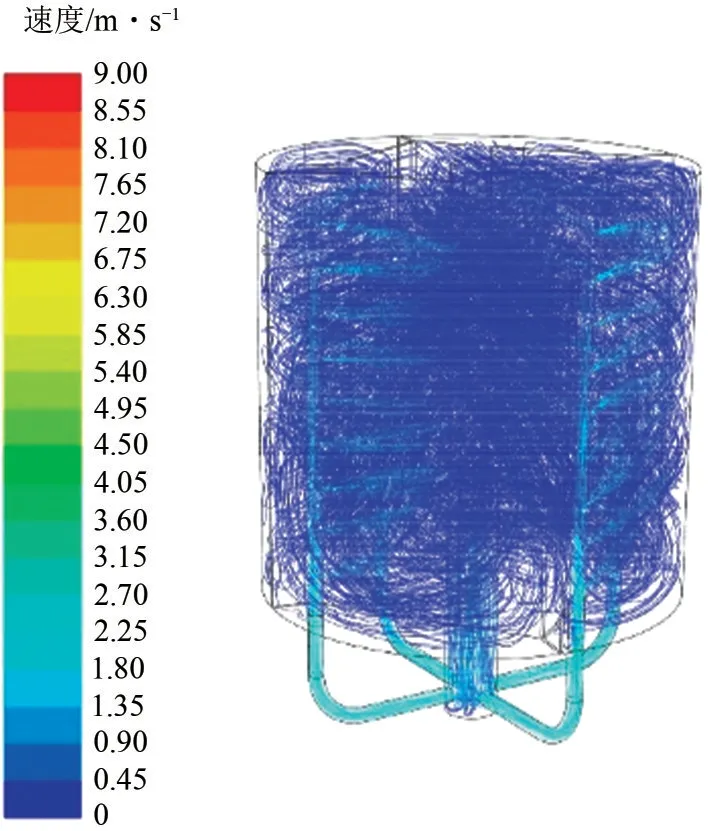
图10 Re=6346时速度迹线图

拉伸率如图11所示，其中L为迹线的长度，D为循环射流混合槽的直径。从图11(a)中可以看出，对称两喷嘴的拉伸率变化趋势相似，且离jet5喷嘴距离越远相似性越高，此外在jet1 与jet9 喷嘴所对应位置处拉伸率较其他喷嘴高；在L/D=0～0.5 附近时受初始高速射流的影响拉伸率呈增大趋势，在L/D=0.5～0.7 附近时，受两股射流之间的卷吸、掺混和涡流扩散的影响，其拉伸效率呈下降趋势；但随迹线长度的增加，受二次射流的影响，其拉伸率出现增长趋势。

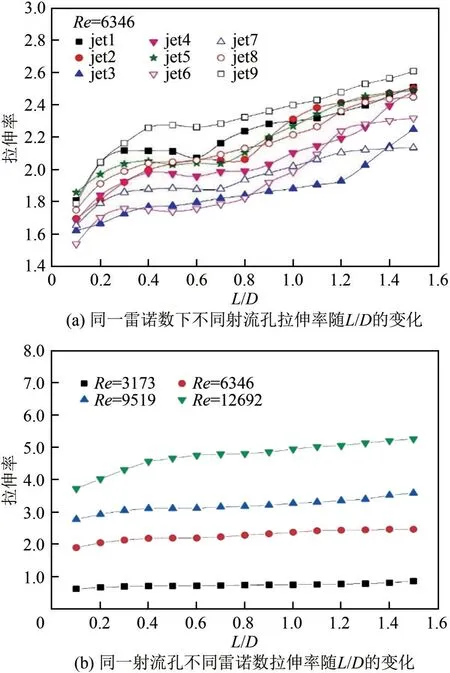
图11 不同条件下的拉伸率变化（t=28s；αd=2.86%）

同一射流孔不同Re下的拉伸率如图11(b)所示，可以看出4种雷诺数下的拉伸率均呈递增趋势，且拉伸率随雷诺数的增大而增大。与Re=3173 相比，Re=6346、9519 和12692 的拉伸率分别提高了289%～320%、418%～454%和607%～667%。因此可以发现随Re的增加，拉伸率的变化呈倍数增加，更加有利于流体的混合，可以提高流体混合的整体速率，缩短混合时间。

3 结论

基于Eulerian-Eulerian 多相流模型与SSTk-ɷ湍流模型，对循环射流混合槽内液液两相量纲为1射流中心线速度、离析强度和拉伸率等参数的流动及混合特性进行研究，得出如下结论。

（1）不同相含率和Re下的射流中心线速度衰减趋势一致，在l/s＜0.4 时αd=1.80%和αd=2.86%时量纲为1射流中心线速度衰减趋势与αd=6.00%相比减弱21%和51%；在l/s＜0.24 时Re=6346、9519 和12692 时量纲为1 射流中心线速度衰减趋势与Re=3173 相比减弱2.6%、2.87%和12.69%；受升力及卷吸效应的影响，在jet1～jet4喷嘴位置处的射流中心线往上偏移，在jet1与CJT 的底部形成强制涡加速混合。

（2）离析强度随混合时间增大而减小，在高速射流的影响下，射流中心线两侧形成强制涡，导致不同周向角下的离析强度受强制涡、卷吸及掺混作用的影响呈W 形趋势；降液管内部由于液滴聚并的影响，导致不同r/R的离析强度与其他区域相比较大。

（3）柱状加料方式与对称球状加料方式下离析强度随混合时间的增大呈下降趋势，且对称球状加料方式下的混合时间比柱状加料方式下的混合时间减少65.5%；在l/s＜0.38 范围内对称球状加料方式下的量纲为1射流中心线速度衰减趋势与柱状加料方式相比减弱14.2%。

（4）在同一雷诺数不同射流孔条件下，关于中心对称的两射流孔拉伸率趋势相似，jet1 与jet9 处拉伸率与其他射流孔相比较高。在同一射流孔不同雷诺数的条件下拉伸率随Re的增加而增大，在Re=6346、9519 和12692 时拉伸率与Re=3173 时相比分别提高了289%～320%、418%～454%和607%～667%。

符号说明

c—— 浓度

CoV—— 变异系数

D—— 循环射流混合槽直径，mm

dj—— 射流孔直径，mm

dp—— Patch球体直径，mm

H—— 循环射流混合槽槽体高度，mm

h—— Patch分散相高度，mm

L—— 迹线长度，mm

l—— 射流中心线长度，mm

Q—— 体积流量，m3/h

R—— 循环射流混合槽半径，mm