基于LSTM的空间机器人系统惯性张量在轨辨识
2021-11-30初未萌杨今朝邬树楠吴志刚
初未萌,杨今朝,邬树楠,吴志刚
1.大连理工大学 航空航天学院,大连 116024
2.大连理工大学 工业装备结构分析国家重点实验室,大连 116024
随着在轨航天器的逐年增多,空间中充斥着大量因燃料耗尽或故障等原因造成失控的航天器[1-3]。这些失控的航天器一般为惯性参数未知的非合作目标,严重影响空间轨道上其他正常运行航天器的安全。针对这一问题,目前世界各国都在大力发展基于空间机器人的在轨服务技术,以实现对失控航天器的抓捕与维修[1]。空间机器人在抓捕目标的过程中需要改变其本身构型,整体系统的惯性张量会随时间产生较大变化,特别是目标被捕获瞬间会造成系统惯性张量的突变。如果无法了解构型改变以及目标抓捕对整体系统惯性张量的影响,当系统在抓捕过程中发生非预期改变时将不能实现有效的整体姿态控制。因此,对空间机器人整个抓捕过程的惯性张量进行在轨实时辨识是十分必要的。
目前,涉及空间机器人惯性张量辨识方面的研究已经取得了许多成果。Murotsu等[4]根据空间机器人机械臂关节运动所引起的整体位姿变化,分别运用基于动量守恒原理与基于Newton-Euler运动方程2种辨识方法对抓捕目标惯性参数进行辨识。王明等[5]基于机械臂的运动实现了对组合航天器惯性参数的辨识。侯振东等[6]提出了一种基于推力器激励的组合航天器惯性参数辨识方法。张博等[7]采用自适应反作用零空间控制方法,使得空间机器人可以在基体姿态扰动最小的情况下,辨识捕获的大型非合作目标的惯性参数。Chu等[8]直接利用机械臂末端执行器抓捕目标所反馈的接触力信息辨识其惯性参数。Xu等[9]提出的方法首先需要对整个组合航天器的惯性参数进行辨识,然后利用辨识出的参数来推导组合航天器各子部分的惯性参数。以上方法对空间机器人惯性张量的辨识都达到了较高精度,但是这些方法主要解决的是目标已被捕获且所辨识的参数是常量的情况,针对在整个抓捕过程中随时间变化且会发生突变的系统惯性张量实时辨识问题的研究则较为少见。
随着人工智能技术的发展,人工神经网络(ANN)、循环神经网络(RNN)等智能技术已经广泛用于众多领域的研究[10-12]。其中RNN中的长短期记忆(Long-Short Term Memory, LSTM)网络在处理复杂时间序列问题上具有较大优势。LSTM网络可以有效捕获复杂时序数据中的长期依赖信息,并进行建模,近年来在时变参数辨识、故障诊断等领域都获得了成功的应用[13-15]。
根据以上分析,针对空间机器人在抓捕失控目标过程中复杂时变的系统惯性张量辨识问题,本文提出一种基于LSTM的系统惯性张量在轨智能辨识方法,并利用仿真数据对采用本文方法构建的参数辨识网络的有效性进行验证。
1 空间机器人建模
对抓捕过程中的空间机器人进行建模可以分为2个阶段:目标捕获前和目标捕获后。研究的目标捕获前空间机器人模型如图1所示,空间机器人是由一个航天器基体和一个具有2个连杆的机械臂组成,机械臂上的每个连杆假设只有一个转动自由度。图1中:ΣI为惯性坐标系;Σ0为航天器基体的体坐标系,原点设在基体质心;Σi(i=1,2)为连杆i的体坐标系,原点位于连杆i前端旋转关节转轴处;r0、r1、r2分别为基体和2个连杆的质心位置矢量;p1、p2分别为2个连杆体坐标系的位置矢量。
在惯性坐标系ΣI下,上述矢量之间的几何关系为
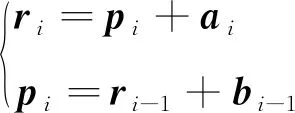
(1)
在目标捕获前空间机器人的运动学方程为
(2)
式中:ai为连杆i体坐标系∑i原点到其质心的位置矢量;b0为基体质心到坐标系∑1原点的位置矢量,b1为连杆1质心到坐标系∑2原点的位置矢量,b2为连杆2质心到其末端的位置矢量;ω0为基体的角速度矢量;ωi为连杆i的角速度矢量;φi为连杆i的角度矢量;i=1,2。
根据以上运动学方程,可以得到在空间机器人目标捕获之前系统的动能为
(3)
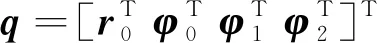
(4)
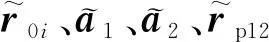
由于空间机器人和目标均为刚体,因此系统不存在弹性势能,且重力势能可忽略不计。由式(3)可得到目标捕获前系统的拉格朗日函数L=Tbc,将其代入第二类拉格朗日方程:
(5)
即可得到目标捕获前空间机器人的动力学方程:
(6)
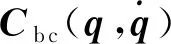
在目标捕获前,空间机器人相对于航天器基体的体坐标系Σ0的整体惯性张量为
(7)
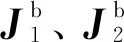
(8)
式中:R1、R2分别为体坐标系Σ1与Σ2相对于Σ0的姿态矩阵。
在目标捕获后,空间机器人示意图如图2所示。为便于分析,对捕获过程进行简化:假设空间机器人与目标不存在相对运动,目标与机械臂一经接触即被捕获,并与连杆2固连在一起,整个捕获过程较为平稳。Σe为目标的体坐标系,原点位于机械臂末端中心处,re、pe分别为目标的质心位置矢量和体坐标系位置矢量。re、pe在惯性坐标系下的几何关系为
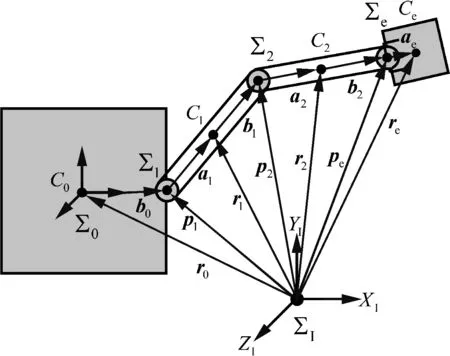
图2 目标捕获后空间机器人示意图
(9)
目标捕获后空间机器人的运动学方程是在式(2) 基础上加上目标的运动学方程,即
(10)
式中:ωe为目标的角速度矢量。
相应的空间机器人目标捕获后的系统动能为
(11)
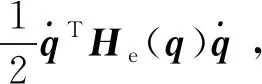
(12)

(13)
目标捕获后的空间机器人相对于航天器基体的体坐标系Σ0的整体惯性张量为
(14)
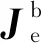
(15)
式中:Re为体坐标系Σe相对于Σ0的姿态矩阵。
2 基于LSTM的参数辨识网络
2.1 训练数据生成
在构建基于LSTM的参数辨识网络之前需要获得足量的数据对网络进行训练,本节对训练数据生成过程进行详细介绍。
假设给定空间机器人初始状态、受力情况、最终目标构型及抓捕过程时长,对每个空间目标所执行的抓捕策略可以描述为:在目标捕获前驱动空间机器人机械臂从初始状态逐渐伸展,直至完全展开捕获目标,捕获到目标后收回机械臂将目标拉至后续控制所需的目标构型。
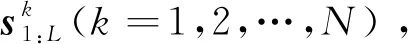

Jt=[JxxJyyJzzJxyJxzJyz]t
(16)
为使训练效果尽量不受Jt量级大小的影响,需对Jt中的每个元素分别进行归一化处理:
(17)
2.2 参数辨识网络构建

LSTM网络如图3所示,可以看到LSTM网络是多个LSTM cell组成的,LSTM cell的数目与输入序列长度相同,其输出为网络最后一个LSTM cell输出hl。LSTM cell可以利用遗忘门、输入门和输出门3个门来控制沿数据序列的信息传递[13],其计算方法为
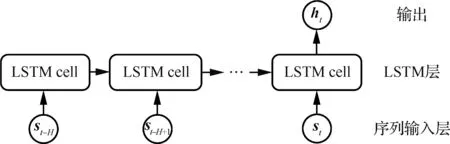
图3 LSTM网络
(18)
式中:st为cell的输入向量;ft、it、ot分别为cell内的遗忘门值、输入门值和输出门值;ct、lt分别代表cell产生的候选记忆和新记忆;bf、bi、bo、bc分别为对应的偏移向量;Wf、Wi、Wo、Wc分别为对应的输入权重矩阵;Uf、Ui、Uo、Uc分别为对应的回归权重矩阵;ht为cell内隐含层的输出向量,也是cell的输出向量,其维度由隐含层的结点数确定;σ、tanh分别为sigmoid激活函数与双曲正切激活函数。
多层全连接网络结构如图4所示,它由1个输入层、2个隐含层及1个输出层组成。输入层接收LSTM网络的输出量hl并将其导入至隐含层中进行计算。
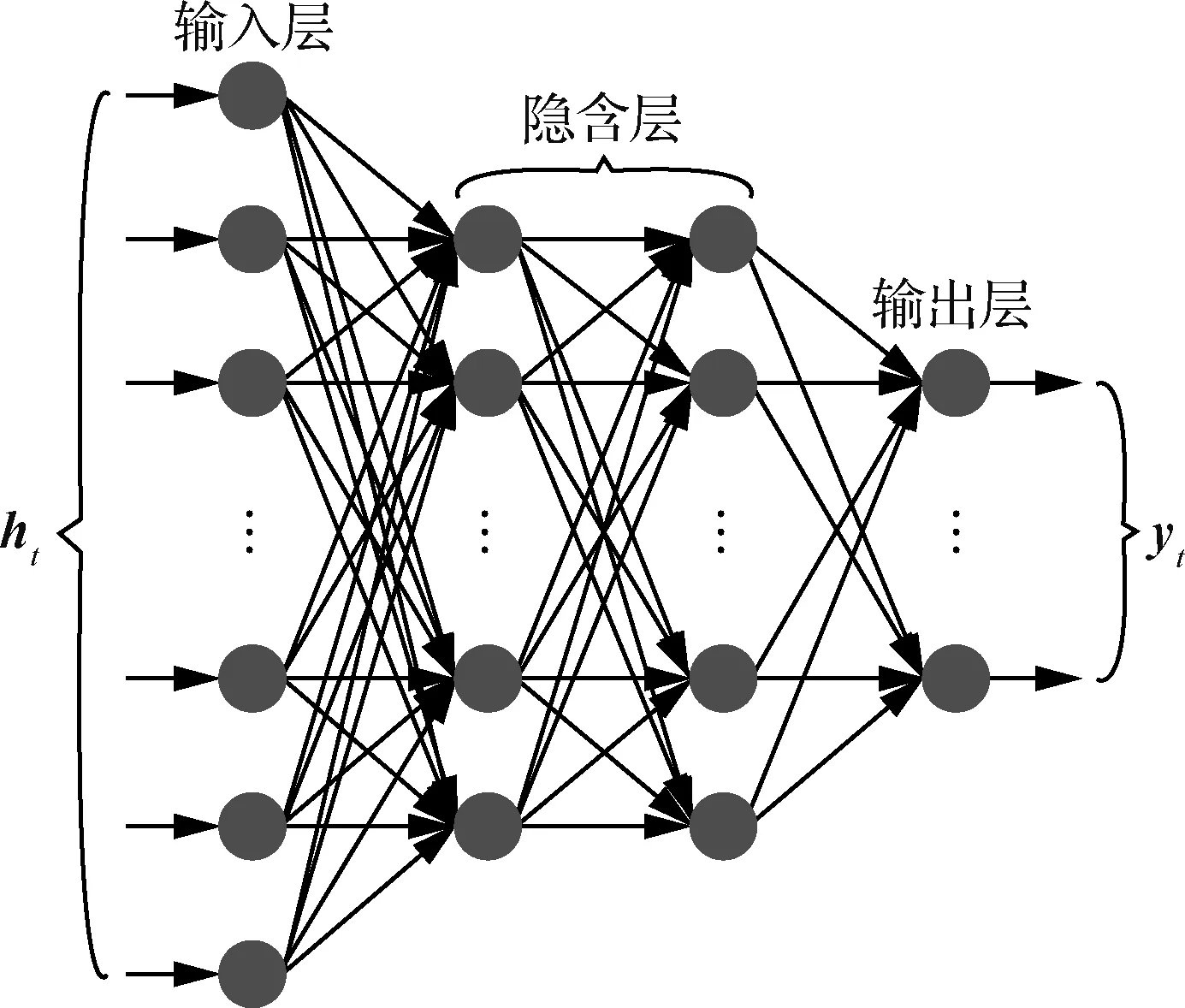
图4 多层全连接网络
单层隐含层的计算方法为
(19)
式中:yi-1为第i-1隐含层的输出量;Wi、bi分别为对应的权重矩阵与偏移向量;xi为第i隐含层的输入量;yi为当前隐含层的输出量;f(·)表示非线性激活函数,本文选取的激活函数是ReLU函数[18]。
最后一个隐含层的输出yl被输入至一个线性回归层(输出层)中并输出辨识结果:
(20)
式中:WO、bO分别为输出层的权重矩阵与偏移向量;yt为t时刻网络辨识的空间机器人整体惯性张量。
2.3 模型训练
在参数辨识网络构建完成后需要对其进行训练以实现既定的目标。训练过程如图5所示。
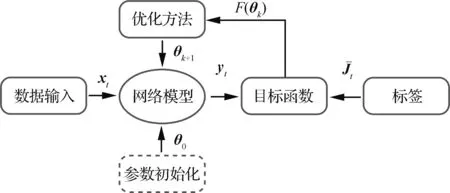
图5 训练过程
首先对网络模型参数进行初始化,对于LSTM网络参数采用的是正态分布随机初始化方法,而对于全连接网络参数采用的是MSRA(Microsoft Research Asia)初始化[19]。MSRA初始化主要应用于激活函数为ReLU函数的网络模型,该方法可以使模型各层的前向输出方差保持一致,保证层间传递的信息受层数的影响较小,从而提高模型训练的收敛速度。然后设定目标函数,由于惯性张量辨识是一个回归问题,因此目标函数被设为网络辨识输出与标签之间的均方误差(MSE):
(21)
式中:F(θ)为目标函数;θ代表网络模型中所有参数;M为训练集中的样本总个数。设定好目标函数后,采用Adam优化方法对网络模型参数进行优化,优化目标为最小化F(θ)[20]。Adam优化方法通过估计目标函数中参数梯度的一阶矩和二阶矩,实现了对学习率的自适应调整,可以有效提升模型的训练效率。最后在训练过程中不断优化迭代直至F(θ)小于一定范围或达到预定的迭代次数时,参数辨识模型完成训练。
3 数值仿真验证
所研究的空间机器人参数如表1所示。假设只在平面执行空间机器人的整个抓捕过程,并采用PD(Proportion Differentiation)控制策略对空间机器人进行控制。目标捕获前后对空间机器人的控制目标如下。
目标捕获前,对基体、连杆1和连杆2的控制目标分别为
(22)
(23)
式中:tc为捕获到目标的时刻。
目标捕获后,对基体、连杆1和连杆2的控制目标分别为
(24)
(25)
式中:te为抓捕过程完成的时刻。本文设定的tc、te分别为50、100 s。
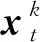

表1 空间机器人参数和目标
表2 生成训练集所需参数
在参数辨识网络构建方面,设LSTM网络的隐含层结点数为40,全连接网络的2个隐含层神经元数也为40。训练过程中设定优化方法的学习率为0.001,批处理样本量为20,对整个训练集的训练次数为50。为验证所提方法的有效性,采用与生成训练集相同的方法,随机生成了30组与训练集不同的数据组成测试集。
模型在N=200的训练集上进行训练的MSE曲线如图6所示。从图中可以看出,随着迭代次数的增加,根据目标函数计算的MSE曲线整体上呈下降趋势。在2×105次迭代之前,MSE曲线收敛速度较快但存在较大振荡,随后曲线的收敛逐渐趋于平稳并维持在较低水平。这说明所采用的训练方法可以保证MSE曲线在训练过程中快速且高精度地收敛。训练完毕后,分析训练集大小对网络模型精度的影响如表3所示,当N=50时,即训练集数据量较小的情况下,模型在训练集与测试集上的性能表现存在较大的差异。当数据量达到一定水平后,这种差异明显降低。而且随着训练集大小的增加,模型精度不断得到提升,因此增加训练集的大小可以有效地提高模型的精度,并减少模型过拟合的风险。不过训练集过大会增加数据的获取成本,且会降低模型训练的收敛速度,因此需要对以上情况进行综合分析来选取合适的训练集大小[21]。
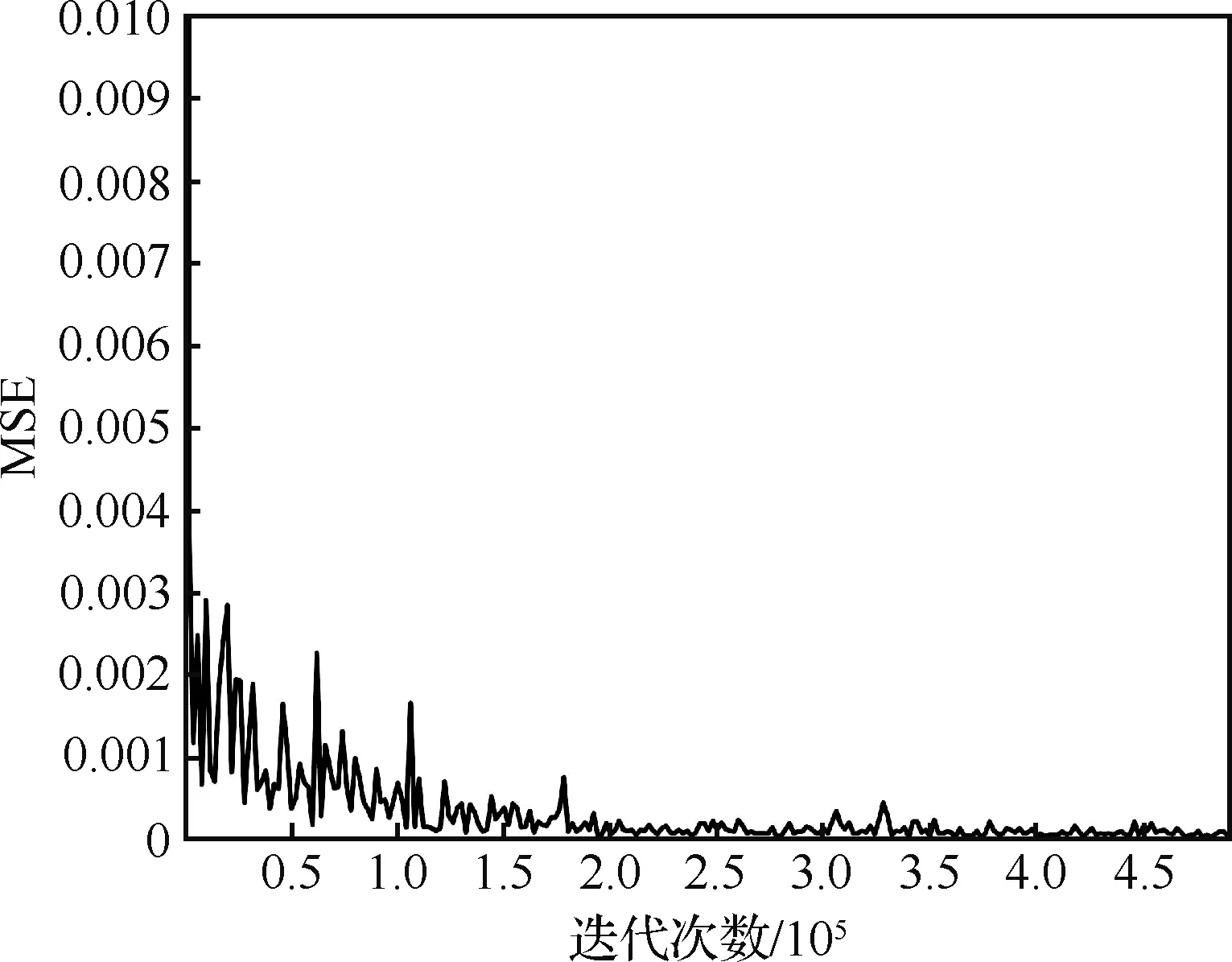
图6 训练过程中的MSE曲线
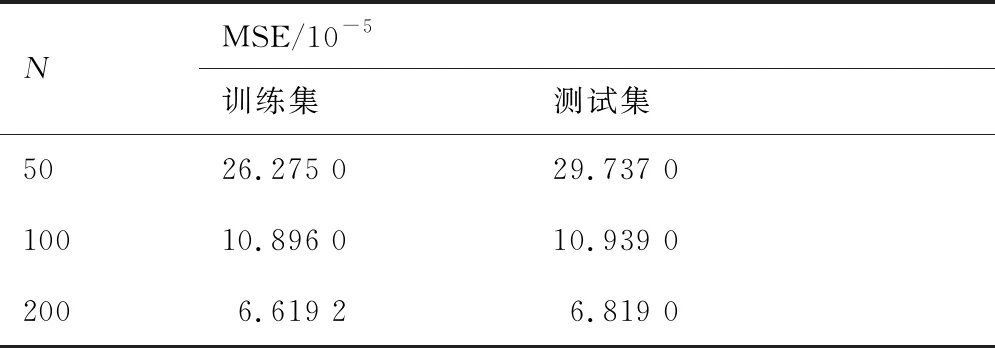
表3 训练集大小的影响
为验证本文所提参数辨识网络的辨识效果,选取了测试集中一组数据的辨识结果进行展示,这组数据对应的目标参数如表4所示。图7是抓捕该目标时对连杆施加的驱动力矩时程曲线。抓捕过程系统惯性张量在轨辨识结果如图8所示。从图8可以看到,采用一定目标参数范围生成的训练数据训练的参数辨识网络有效地实现了对非合作目标抓捕过程系统惯性张量的辨识,其所计算的辨识曲线与真实曲线基本重合。特别是对于Jyy、Jzz在50 s捕获到目标时所产生的明显突变,本文方法仍能精确辨识出突变的参数且仅产生了较小的误差波动。不过当测量噪声的量级较大时,本文方法的辨识精度也会有所降低。
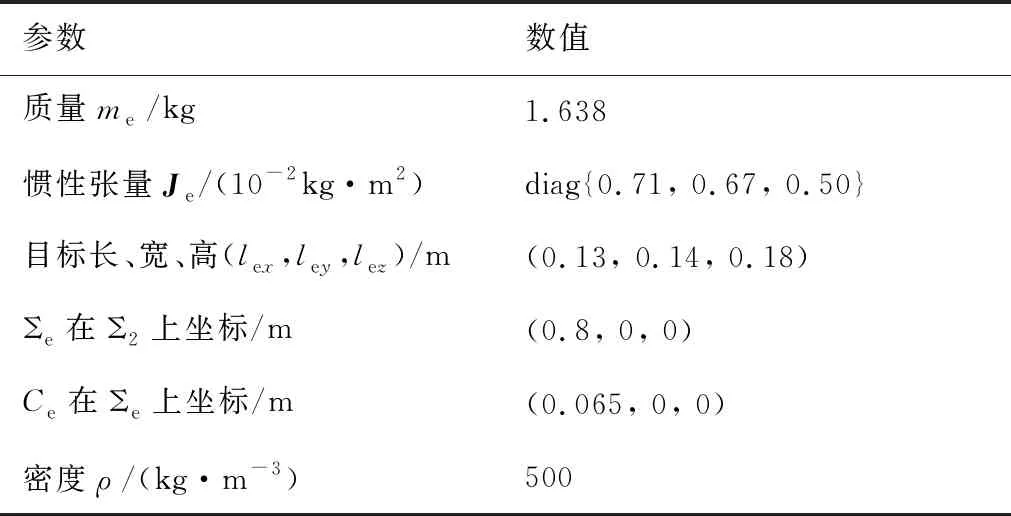
表4 目标参数
表5给出了本文方法与基于RNN的参数辨识网络在测试集上的辨识性能对比。性能对比采用平均相对辨识误差(MIRE)作为标准,其公式为
(26)

如表5所示,本文方法对这4个参数的辨识精度明显高于基于RNN的参数辨识网络,而且对主惯量Jxx、Jyy、Jzz的辨识尤为精确。虽然对Jyy、Jzz的辨识精度相对于Jzz有所降低,这主要是由于Jyy、Jzz惯性张量曲线的突变所造成的,但其平均相对误差仍然维持在10-4数量级这样较低的水平。在实时性方面,本文方法的单步辨识时间约为3×10-3s,是可以满足在轨辨识任务的实时性要求。因此以上结果进一步显示了本文所提出的基于LSTM的参数辨识网络的有效性与可行性。

表5 辨识性能对比
为进一步明确参数范围设定对模型辨识精度的影响,对使用3种不同参数范围训练的模型精度进行比较,每个模型都采用了与上述仿真相同的结构与训练策略。如表6所示,随着目标长宽高范围的增加,模型对测试集的MSE显著增加。这其中一个原因是当长、宽、高3个参数范围增加时,参数整体取值的可能组合将会呈指数级增加。即当3个参数范围同时增加k倍时,参数取值的可能组合就会增加(1+k)3-1倍。根据表3所示,在[0.10, 0.20]范围内选取了200组不同的目标长宽高组合进行训练即可获得较高的辨识精度。但当范围增大的情况下,当前的数据量就不能充分地表征该范围内的数据分布特性,因此需要更多组的参数用于训练来提高辨识精度。另一方面,由于参数范围的增加,其状态-控制序列与参数之间的映射也变得更加复杂,因此需要根据任务目标调整网络模型的节点数,加强其非线性拟合能力,从而提升模型的辨识精度。
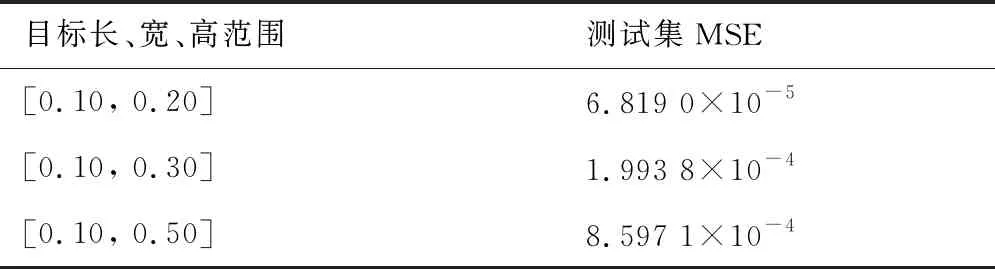
表6 模型辨识精度在不同参数范围下的比较
4 结 论
利用LSTM构建参数辨识网络,实现了对空间机器人抓捕非合作目标过程中系统惯性张量的在轨辨识。
1) 使用在预先设定的目标参数范围内随机生成的训练数据对参数辨识模型进行训练,所训练的模型能够有效地执行在同一范围内目标参数未知情况下的系统惯性张量辨识任务。
2) 在测量噪声存在的情况下,所构建的参数辨识网络能够实时且准确地辨识时变的系统惯性张量,即使在参数发生突变时辨识结果仍然十分精确。仿真结果显示,本文方法辨识主惯量Jxx、Jyy、Jzz的平均相对误差数量级为10-4,辨识惯性积Jxy的平均相对误差数量级为10-3。
