大范围收敛的摄动Lambert问题新型解法：拟线性化-局部变分迭代法

2021-11-30冯浩阳岳晓奎汪雪川

航空学报 2021年11期

冯浩阳,岳晓奎,汪雪川,*

1.西北工业大学航天飞行动力学技术国家级重点实验室,西安 710072

2.西北工业大学航天学院,西安 710072

Lambert问题是航天动力学领域的经典问题,很多学者对其进行研究并提出了不同的解决方法。在工程领域,由于摄动Lambert问题不具备解析解,因此主要通过数值方法进行求解。常用的摄动Lambert问题解法主要包括两类,一类是将其转换为初值问题进行迭代求解,另一类是通过离散化方法将其转换为非线性代数方程组进行求解。

将边值问题转换为初值问题的方法中,最具代表性的方法即打靶法。打靶法[1-2](Shooting Method)把两点边值问题转化为初值问题,并使用牛顿法(Newton’s Method)对初速度进行迭代修正,该方法虽然具有收敛速度快的优点,但其收敛域很小且对初值非常敏感,实际应用缺陷较大。多重打靶法[3]融合了有限差分法和打靶法,它将整个求解区间划分为多个子区间,并在各个子区间上求解初值问题,相对于简单打靶法,该方法具有更大的收敛域,但仍具有计算不稳定的缺陷,且在各个子区间的边界上存在速度不连续的问题。隐式打靶法[4]在间接法思想的基础上,借助尺度变换法和变分法,在求解包含隐式终端约束的轨道优化问题中得到应用。直接变换法[5-6]能够将两点边值问题转化为一对初值问题,计算简便,但该方法对微分方程的形式和边值条件有特定要求,对于一般的非线性两点边值问题并不适用。其他方法如Gooding给出了迭代变量的最优起始公式[7],得到了在所有情形下都可以迅速收敛的高精度Lambert问题算法,Battin通过迭代高斯方程[8]得到Lambert问题的解,但是这些经典方法都不适用于一般的摄动Lambert问题。

在边值问题的离散化方法中,有限差分法[9]的应用较早,通过差分估计将转移轨迹离散为大量的差分节点,进而对其进行代数求解。然而有限差分法需要建立大规模非线性代数矩阵方程,并且需要存储大量节点数据。对于大范围轨道转移的摄动Lambert问题,有限差分法不仅求解困难,其数值计算精度也较低。配点法[10]也是求解初值问题和两点边值问题的重要方法,该方法使用基函数对时间域内的配点插值,从而得到半解析解,且无需存储大量的离散数据[11]。NK/C伪谱法[12]使用Chebyshev正交多项式作为插值基函数,在求解Lambert问题、相对轨道转移等航天动力学问题中得到应用。径向基函数(RBFs)方法[13]则使用径向基函数对配点插值,在求解二体问题中得到应用。配点法具有精确高效的优点,但在计算过程中需要对雅克比矩阵求逆,这通常比较繁琐。修正Chebyshev-Picard迭代法(MCPI)[14]利用Picard迭代构造出修正公式,通过正交多项式插值逼近真实解,避免了矩阵求逆。反馈加速Picard迭代法[15]对修正变分迭代法[16]进行改进,并融合了配点法的思想,使用第一类Chebyshev正交多项式对配点插值,得到了一种可用于摄动轨道递推和摄动Lambert问题的新型算法。受算法特点所限,该方法的递推公式需要在整个时间区间上迭代,为了达到较高计算精度需要设置较多的配点和较多的基函数,使计算量增加。

本文提出一种基于拟线性化和局部变分迭代法的摄动Lambert问题求解方法,该方法能够一般性的应用于地球卫星轨道、相对运动轨道、深空轨道等不同轨道类型的转移问题中,为地球卫星的单圈或多圈轨道转移、航天器的交会对接、多航天器编队飞行、深空探测等任务提供稳定、精确、实时的轨道转移算法。在摄动Lambert问题中,使用拟线性化[17](Quasi Linearization)法将摄动Lambert问题转化为迭代形式的线性边值问题,通过叠加法将线性边值问题分解为两个初值问题,并得到初速度和转移轨道的迭代公式。与传统打靶法相比,其迭代格式更加简单,计算更加稳定,且收敛域显著增大。在初值问题的解算方面,本文利用了局部变分迭代法[18-19](Local Variational Iteration Method)精确高效的优点,在计算过程中不涉及非线性代数方程组的矩阵求逆操作,因此计算简便高效。在此基础上提出的拟线性化-局部变分迭代法(QL-LVIM),经过较少的几次迭代,计算结果即可达到很高精度。在初值选取方面,避免了常用的通过二体模型确定初始估计的步骤,可以通过更简洁的方式进行确定。该方法不仅具有与牛顿打靶法相当的快速收敛性,还克服了传统打靶法初值敏感、收敛域小的缺点,并且在同等计算精度下,能够显著提高计算效率。该方法的精确性、稳定性和实时性在低轨转移和高轨转移情形下得到了验证,结果表明,相对于对比方法,本方法在计算效率和收敛域方面具有明显优势。通过地-月系三体转移问题对方法的适用性进行进一步验证。此外,文献[17]中拟线性化方法仅用于求解一维两点边值问题,本文探究了该方法在多维两点边值问题求解中的应用。

1 问题描述

1.1 非线性边值问题的拟线性化

考虑两点边值问题,对于如下非线性二阶微分方程:

y″=f(t,y,y′)

(1)

满足如下边界条件：

y(t0)=y0,y(tf)=yf

(2)

式中：y′=dy/dt,y″=d2y/dt2。

式(1)可以改写为

φ(t,y,y′,y″)=y″-f(t,y,y′)=0

(3)

为得到迭代方程,令yn和yn+1分别表示第n次和第n+1次迭代结果,并且均满足φ=0,对第n次迭代,有

(4)

将第n+1次迭代结果展开有

φ(t,yn+1,y′n+1,y″n+1)=φ(t,yn,y′n,y″n)+

(5)

略去二阶及以上偏导数,式(5)可简化为

(y″n+1-y″n)+…=0

(6)

将式(4)代入式(6)可得

(7)

对应的边界条件为

yn+1(t0)=y0,yn+1(tf)=yf

(8)

则式(1)和式(2)构成的非线性两点边值问题被转化为式(7)和式(8)构成的迭代形式的线性两点边值问题,通过对其多次求解和迭代,即可不断逼近原非线性两点边值问题的解。在拟线性化处理中,虽然忽略了二阶及以上偏导数,但通过多次迭代,仍可以使计算结果达到较高精度。

1.2 摄动Lambert问题的拟线性化

航天器在绕地球运行中,会受到地球非球形摄动、大气阻力摄动、日月摄动、太阳光压摄动等干扰。在近地轨道,主要摄动因素为地球非球形摄动和大气阻力摄动,在中高轨道,主要摄动因素为地球非球形摄动[20-21],这里考虑地球非球形摄动和大气阻力摄动,忽略其他高阶小摄动力的影响。在赤道惯性坐标系下,航天器的轨道动力学方程为

(9)

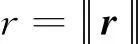
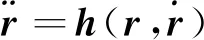
(10)

记轨道转移时间为tf,边值条件为

r(t0)=r0

(11)

r(tf)=rf

(12)

(13)

rn+1(t0)=r0

(14)

rn+1(tf)=rf

(15)

1.3 通过叠加法求解拟线性化形式的Lambert问题

为求解式(13),使用叠加法[17]将rn+1写为

rn+1=V+W·s

(16)

式中:V和W为分运动的位置矢量;s为飞行器在转移轨道起点处的速度,即

(17)

在t0时刻,初值条件式(14)满足：

rn+1(t0)=V(t0)+W(t0)·s=r0

(18)

(19)

为应用叠加法,将约束(18)和(19)做如下分解:

式中:03×3为3阶零矩阵;03×1为3×1零向量,E3×3为3阶单位阵。则式(13)～式(15) 构成的两点边值问题被分解为如下两个初值问题。

1) 初值问题Ⅰ

(20)

(21)

2) 初值问题Ⅱ

(22)

(23)

利用边值条件(15)有

rn+1(tf)=V(tf)+W(tf)·s=rf

(24)

s=W(tf)-1·[rf-V(tf)]

(25)

不同于对初值敏感的牛顿法,拟线性化方法具有较大的收敛域,在确定边值问题的初始估计解时可以较为随意,这里以连接2个边界点的线段作为初始估计解。另外,由于03×3和E3×3均为3×3矩阵,直接求解初值问题Ⅱ比较繁琐,此时可以将其分解为x、y、z方向上的3个子问题,并分别求解,由3个子问题的求解结果合并得到W,注意图1中rn,n=0表示初始估计解而非转移轨道的初始位置。

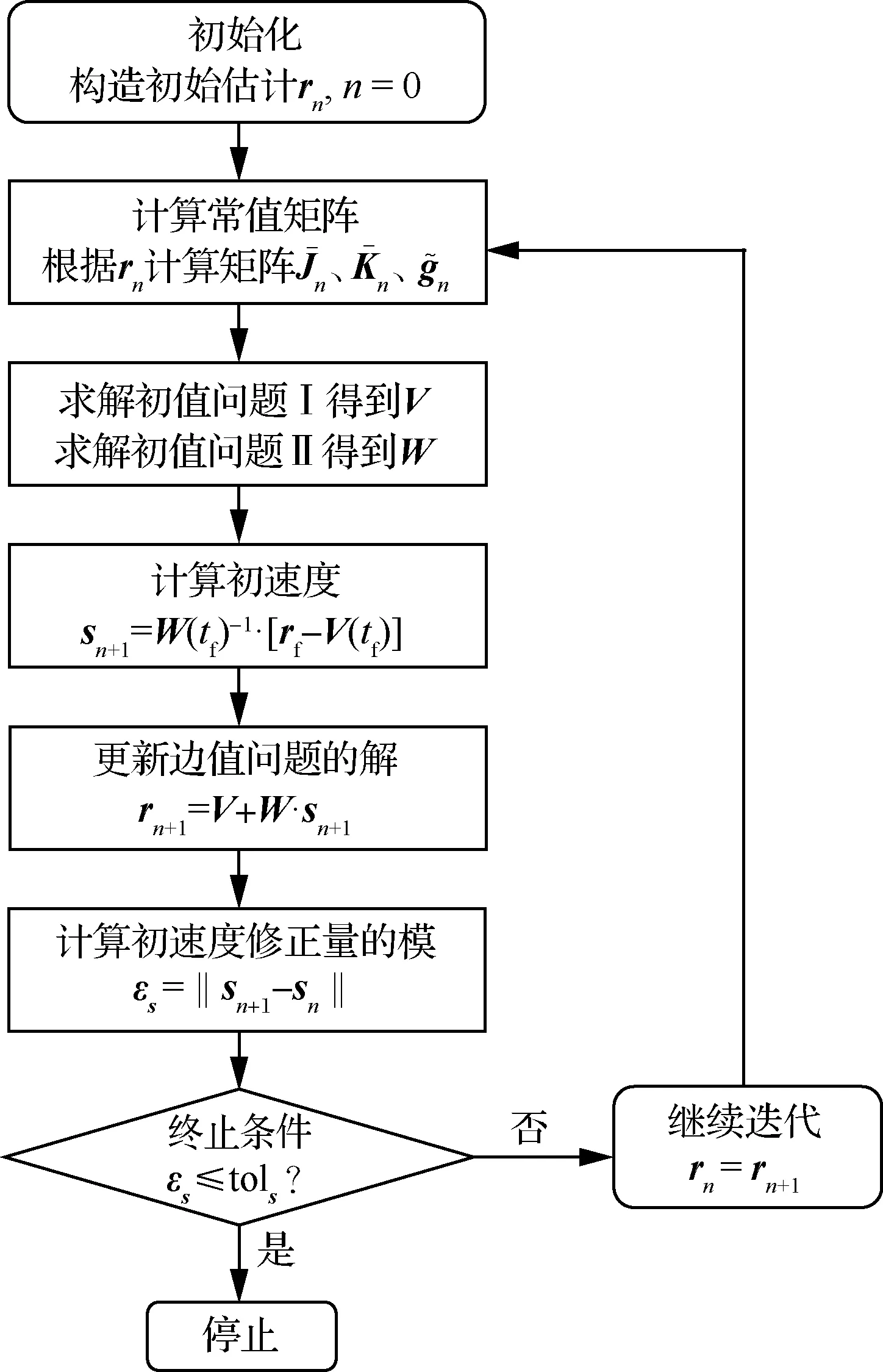
图1 拟线性化法求解Lambert问题的流程

1.4 局部变分迭代法对初值问题的求解

经典的求解初值问题的方法有欧拉法、龙格库塔方法、线性多步法等,为得到较高精度的解,这些方法需要设置较小的步长,造成计算耗时较长,并且需要存储大量的节点数据。局部变分迭代法也是求解初值问题的方法之一,并具有精确高效的优点,计算中选取较大的步长就可以达到较高的计算精度,且无需存储大量节点数据,这里使用该方法对以上2个初值问题进行求解。对于如下一阶非线性微分方程：

(26)

x(t)=[x1(t),x2(t),…,xd(t),…,xD(t)]T为随时间变化的D维矢量。首先给出方程解的初始估计,记为x0(τ),随后在求解区间内对其进行多次修正,从而不断逼近方程的真实解,迭代公式为

τ]}dτ

(27)

式中:λ(τ)为待定的拉格朗日乘子矩阵。式(27)表明,近似解xn+1包括2部分,一部分为xn,另一部分为xn在t时刻之前累计偏差的加权平均。若使式(27)右端关于xn不变,则右端的变分为零,由此可以得到如下约束：

(28)

式中：t0≤τ≤t;I为单位阵;J(τ)=∂g(xn,τ)/∂xn。将λ(τ)在τ=t处做一阶泰勒展开,可以得到

λ(τ)≈-I+J(t)(τ-t)

(29)

(30)

通过在时间域配点可以将式(30)离散化,记t1,t2,…,tM为配点时刻,则由式(30)可得

(31)

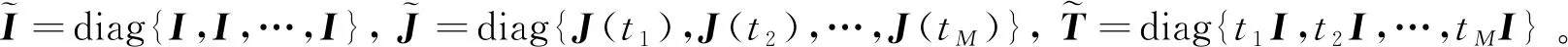
(32)

式中：Φd=[φd,1(t),φd,2,…,φd,N(t)]为基函数系;Ad=[αd,1(t),αd,2(t),…,αd,N(t)]T为基函数的系数矢量。当x(t)的各分量用相同的正交基函数表示时,编程会大大简化,因此将Φd(t)统一写为Φ(t)。根据式(32)有

(33)

(34)

对于第n次迭代,

(35)

式中：G(t)=[G1(t),G2(t),…,Gd(t),…,GD(t)]T为D维矢量。通过正交基函数插值,将Gd表示为

(36)

式中：Φ(t)=[φ1(t),φ2(t),…,φN(t)],Bd=[βd,1(t),βd,2(t),…,βd,N(t)]T,对xd(t)和Gd(t)的插值使用相同的基函数Φ(t)。在t1,t2,…,tM时刻,由式(36)可得

(37)

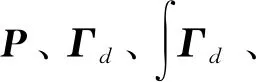
(38)

类似地可以得到

(39)

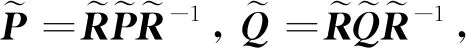
(40)

可以得到迭代公式为

(41)

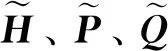
2 求解验证

2.1 计算精度和效率分析

本节使用QL-LVIM对摄动Lambert问题进行求解,并与另外4种求解两点边值问题的方法进行对比。打靶法是求解两点边值问题的经典方法之一,利用牛顿法可以得到初速度的迭代公式,并将两点边值问题转化为两个初值问题,若通过经典的四阶龙格库塔方法(RK4)对初值问题进行求解,就得到了牛顿-四阶龙格库塔方法(Newton-RK4),这里将其作为第1种对比方法。同时,将牛顿法与局部变分迭代法结合,构造Newton-LVIM作为第2种对比方法。牛顿法具有初值敏感性,当初始估计与实际初速度偏差不是很大时,才可以保证算法收敛。为了观察大范围收敛情况下不同方法的精度和效率,构造拟线性化-四阶龙格库塔方法(QL-RK4)作为第3种对比方法。最后,与文献[15]提出的反馈加速Picard迭代(FAPI)方法对比,该方法具有精度高、效率高的特点。本文使用联想笔记本R480(CPU： Intel Core i5-8250U；RAM：8.00 G)安装的MATLAB R2017a软件进行数值仿真,未采用GPU加速和并行计算。

表1 摄动Lambert问题的边值条件和转移时间

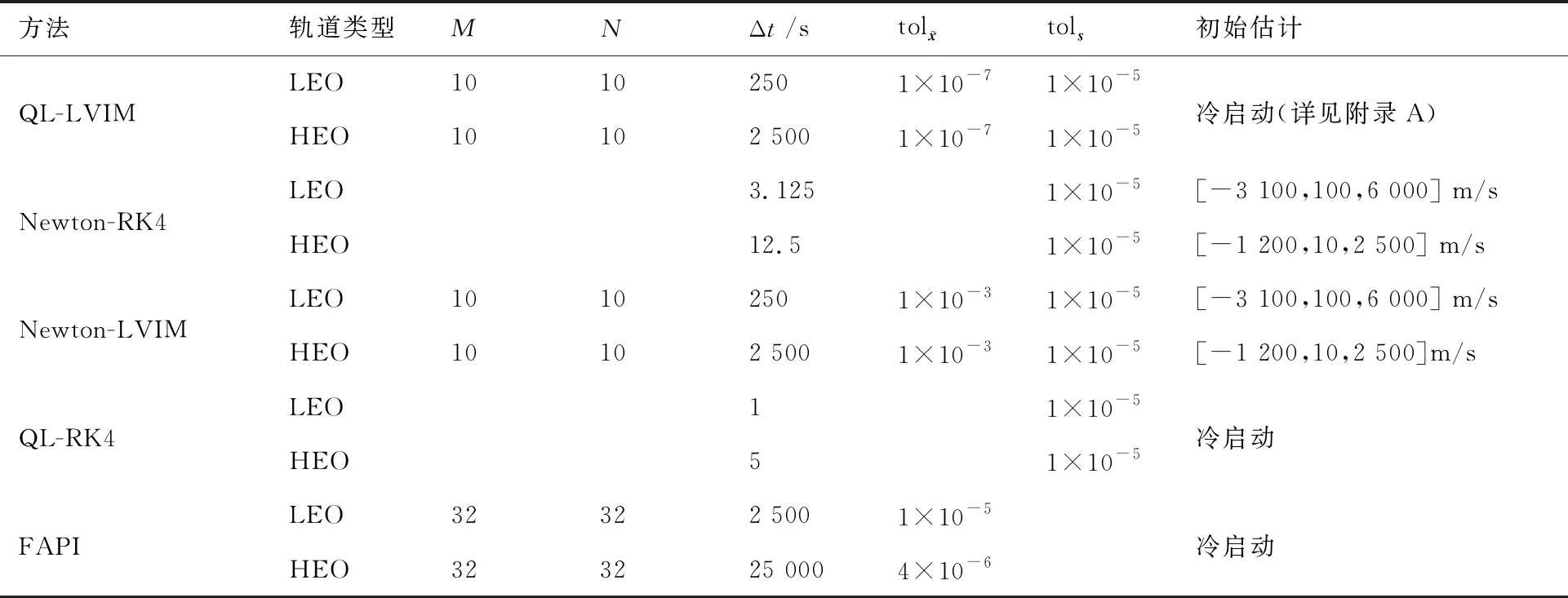
表2 计算参数

初始估计解可以通过多种方法确定,这里选取连接初始位置和末位置的匀速直线轨道,这种初始估计也被称作“冷启动”(详见附录A)。求解后得到低轨和高轨的转移轨道如图2所示,作为参照,调用MATLAB内置的ODE45函数(将相对误差和绝对误差分别设置为1×10-13和1×10-15),根据QL-LVIM求出的初速度做轨道递推,递推结果也在图2中给出,可以看到QL-LVIM的计算结果和ODE45函数的递推结果能够很好的拟合。

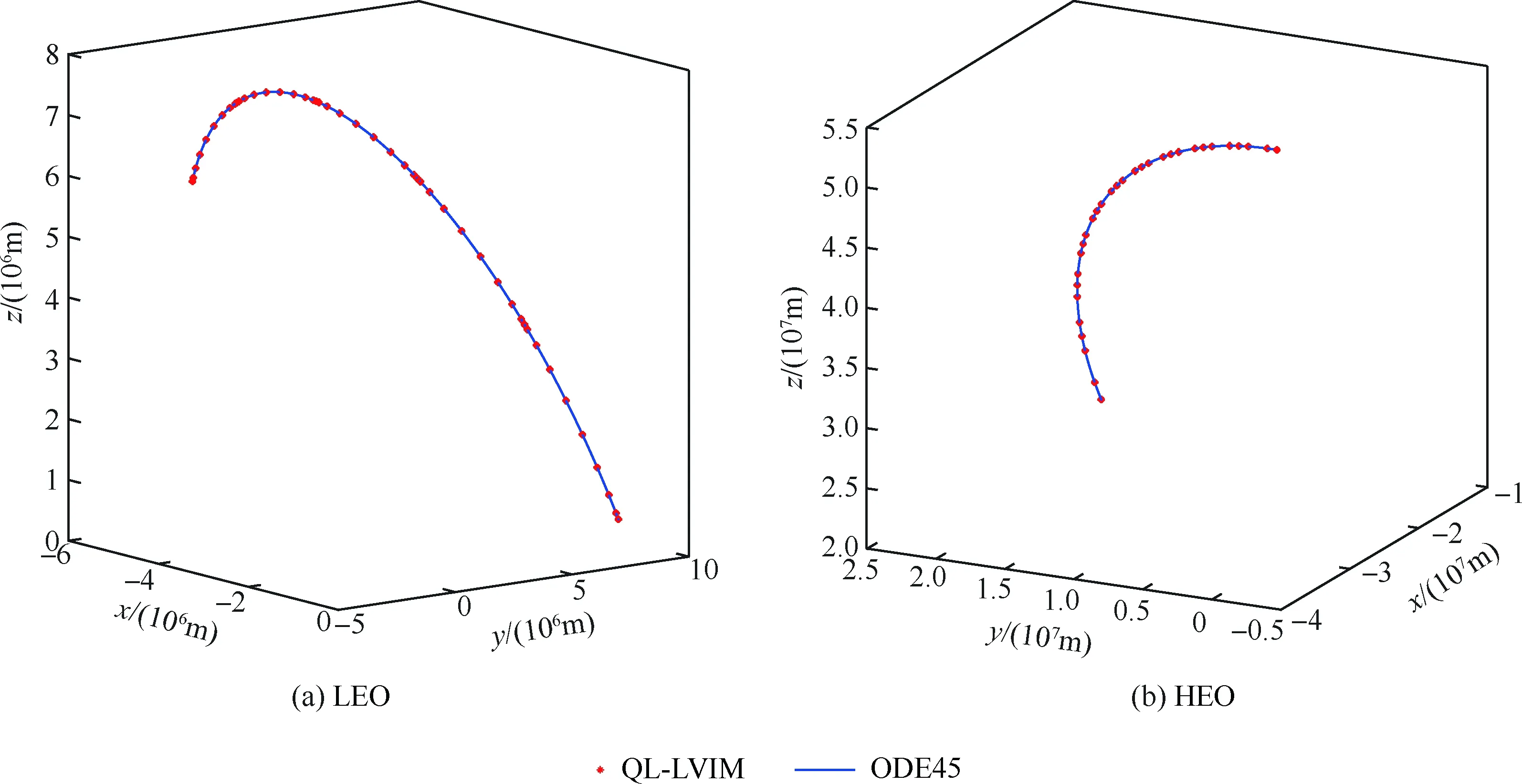
图2 拟线性化-局部变分迭代法的求解结果

为进一步分析QL-LVIM的计算精度和计算效率,将其与Newton-RK4、Newton-LVIM、QL-RK4、FAPI的计算误差和计算时间进行对比,相关参数和初始估计见表2。求解两点边值问题的关键在于求出准确的初速度,初速度的精度反映了算法的精度,因此采用如下方式定义误差：首先求出转移轨道的初速度,再根据起点位置和初速度使用ODE45函数(调至最高精度)做轨道递推,将递推出的终点位置与实际终点位置rf进行比较,则二者的偏差反映了初速度的精度和算法的精度,将该偏差定义为误差。5种方法求出的初速度如表3所示,计算误差和计算时间如表4所示,其中的计算时间为10次计算的平均值。

表3显示,不同算法求出的初速度非常接近,5种算法的有效性得到互相验证。在2种轨道类型下,QL-LVIM、Newton-RK4、Newton-LVIM、FAPI算法求解结果的小数点后6位、后8位完全一致,QL-RK4求解结果的小数点后2位与其他算法一致,表明QL-LVIM、Newton-RK4、Newton-LVIM、FAPI算法精度较高,QL-RK4精度较低。

表4显示,在表2的参数条件下,可以将QL-LVIM、Newton-RK4、Newton-LVIM、FAPI方法的计算误差都调整至1×10-6级别,这能够使不同算法的计算时间更具有可比性。在2种轨道类型下,QL-LVIM的计算时间均最短,其计算速度不同程度的快于其他算法,表明QL-LVIM具有更高的计算效率。而采用QL-RK4方法在经过150 s以上的运算后,精度也只能达到个位数级别,由于更长的计算时间很可能无法满足航天工程中的实时性需要,因此没有必要继续延长计算时间以提高精度。这一结论也与表3的结果吻合。

表3 5种方法计算出的初速度对比

表4 5种方法的计算误差与计算效率对比

QL-LVIM和FAPI都使用了变分迭代的思想,但前者计算速度更快,这是由于在应用FAPI方法时,必须在整个转移区间上迭代,由于时间跨度较大,迭代所需的配点个数和基函数个数较多,参数选择为M=N=32,使得计算量较大,且迭代次数较多。而本文方法克服了这一困难,在求解初值问题时可以将整个转移区间划分为众多子区间,在每个子区间分别迭代求解,在M=N=10时即可达到同样的计算精度。

QL-LVIM和QL-RK4都使用了拟线性化方法,但二者的计算精度和计算效率差异较大,这是由于RK4和LVIM具有不同的计算特点所致。具体来说,2种方法在对初速度进行迭代时,都用到了两个初值问题在终点时刻的计算结果,在RK4方法中,终点之前所有节点的误差都会累积至终点,这造成累积误差严重,计算精度较低,而在LVIM中,前一步长的误差不会累积到下一步长,即终点处的计算结果不受终点之前各节点计算误差的累积影响,因此精度较高。计算中RK4是利用小步长做单点递推,LVIM则是在大步长内对多个配点同时迭代,因此计算效率大大提高。这说明在应用拟线性化方法之后求解初值问题时,LVIM比RK4更有优势。

Newton-RK4与QL-RK4的计算效率和计算精度也差异较大,这是由于在Newton-RK4中,第1个初值问题的微分方程是原非线性微分方程,第2个初值问题的微分方程是原非线性微分方程关于初速度的偏导[17],非线性性质没有损失,因此计算精度较高。而QL-RK4方法中,2个初值问题求解的均为原非线性微分方程拟线性化后的微分方程,非线性性质的丢失造成计算精度的损失,为了提高初速度的精度,就要进一步缩小RK4方法的计算步长,这造成计算量和计算时间增加,但即便如此,计算结果也无法获得令人满意的精度。

虽然Newton-LVIM方法也有较好的计算精度和效率,但该方法仅在初速度估计值比较接近真实值的情况下才有效,这也是Newton打靶法的主要缺陷。相对于Newton法,QL方法的一大优势是具有大收敛域,为分析QL法和Newton法的收敛性,将Newton-LVIM与QL-LVIM进行对比,两种方法均采用LVIM对初值问题进行求解,以排除初值问题求解方法差异对收敛域的影响,对比结果在2.2节给出。

2.2 拟线性化方法与牛顿法的收敛性分析

在工程应用中,算法的收敛性是衡量算法性能优劣的重要标准之一,本节对QL-LVIM和Newton-LVIM的收敛域进行对比分析。由于2种方法的收敛域难以直接精确求出,这里采用蒙特卡罗模拟方法,为2种方法随机选取大量初值,考察在这些初值条件下两种方法的收敛情况。如前文所述,QL法通过对初始估计解(一段运行轨迹)不断迭代得到真实解,Newton法通过对初速度估计值不断迭代得到精确初速度。由于牛顿法不存在通用的初速度估计方法,这里假设,通过二体模型或历史数据大致知道真实初速度的数量级,在此基础上,在以原点为球心、真实初速度的模为半径的球面上随机选取Ns个点,以球心到这Ns个点的矢径做为Ns个初速度估计值,并分别使用Newton-LVIM迭代求解,以验证各个初速度估计值的收敛性。为增强可比性,利用这Ns个初速度和初始位置r0、运行时间tf构造Ns种“冷启动”(详见附录A),做为QL-LVIM的初始估计解,并分析收敛性,相关参数和模拟结果如表5和图3所示。

表5中,对于QL-LVIM方法,在LEO情形下,2 000个初始估计中有1 606个收敛,经计算这些收敛结果的方差为[5.7×10-21, 4.8×10-23, 6.7×-23],表明这些情形均收敛到了真实初速度且具有较高的精度,在HEO情形下,有1 933 个初始估计收敛到了真实初速度,这些结果的方差为[1.35×10-21, 3.36×10-25, 1.96×10-21],2种情形收敛初值的比例均达到80%以上。由于受大气阻力影响更大,LEO情形的初值收敛比例略低。在Newton-LVIM方法下,随机选取的初速度收敛的比例在20%左右,表明在上述随机采样方式下,QL法比Newton法具有更大的收敛域。其原因在于,不同于只对初速度进行迭代的Newton法,QL算法对整条估计轨道上的节点都进行迭代,这使得QL方法收敛域更大。图3 直观展示了2种方法下收敛初值的空间分布。

表5 拟线性化法与牛顿法的收敛性对比

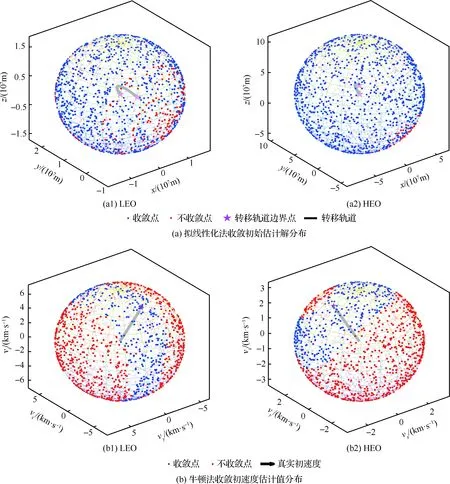
图3 拟线性化法与牛顿法收敛初值分布对比

3 QL-LVIM在三体问题求解中的应用

为验证本文方法在其他轨道转移问题中的适用性,本节对地-月系的圆型限制性三体问题进行求解。

从地球到月球Halo轨道的转移通常借助Halo轨道的稳定流形[23],以地球到月球L1点Halo轨道的转移为例,通常包括2个阶段,第1阶段是航天器从地球停泊轨道到稳定流形的转移,第2阶段是航天器沿着稳定流形的运动,这一阶段不消耗或较少消耗能量。其中,地球轨道到稳定流形的转移轨道要通过大量计算才能确定,传统方法通常先借助蒙特卡罗模拟或经验方法确定一条估计轨道,再通过打靶法将其修正到精确结果。但由于边界条件和转移时间是任意的,这样的轨道搜寻过程较为耗时和不便,这里使用QL-LVIM方法对该问题进行求解。假设转移轨道的起点位于185 km高度的地球停泊轨道,其他初始条件和计算参数见表6。在地-月系统的旋转坐标系下,将地球、月球、航天器分别记为P1、P2、P3,则无量纲形式的航天器运动方程为