基于多类型影响线融合的损伤识别方法研究
2021-11-30曹嘉伟蔡鹏捷黄开哲谢丹妮汪豪杰
曹嘉伟,蔡鹏捷,黄开哲,谢丹妮,汪豪杰
(合肥工业大学土木与水利工程学院,安徽 合肥 230009)
基于单条影响线信息,只有在有限的区域才能相对可信地判断桥梁损伤。有限元法数值解法灵活,适用于复杂问题求解同时,满足工程精度需求。
通过有限元模型研究不同类型影响线对不同损伤工况的敏感性,得到影响线类型对损伤识别的敏感性差异,并进行数值量化。基于D-S证据理论构建新的损伤指标;通过数值模拟,计算出分配给不同影响线的权重,可一定程度上优化已有影响线数据,得到相较于单一类型影响线更精确的数值解答。
1 方法概论
1.1 桥梁建模
利用Midas软件建立三跨连续简支梁模型,采用变箱型截面。将桥梁划分若干个单元,并在相应单元处设置支撑,根据实际情况,将固定铰支节点限制x、y、z方向位移以及x、z方向转动,活动铰支节点限制y、z向位移及x、z向转动。
1.2 损伤及荷载工况设置
为模拟桥梁不同损伤工况,将指定单元材料参数进行改变,例如:将第20-22号单元的材料参数,通过材料弹性模量改变模拟桥梁真实损伤情况,设置损伤级别,判断影响线识别差异。
首先,施加自重静力荷载;再划分车道,模拟车辆设置荷载工况,将荷载组合,输出在移动荷载下的不同影响线。根据后续工作需要,进行大样本的模拟数值训练,对连续梁划分为150个单元,并模拟150种不同位置的桥梁B级损伤,施加车辆移动荷载,输出剪力、挠度、弯矩三种影响线数据。得到450条影响线作为训练样本。
1.3 生成属性模型
为了从不同角度反应不同类型影响线对损伤的敏感程度,要首先解决量纲的冲突问题,采用标准化z-score变换的数据处理方法,即:

根据模拟出的情况,构建相应敏感性指标:域值敏感系数、变化幅值系数、尖锐系数、离散系数。其分别反映了影响线前后变化的范围大小、极差值大小、变化离散程度。因此赋予各种影响线相应的图像属性。
不同类型影响线的变化趋势是不同的,例如剪力影响线是在损伤位置产生断面形式的突变,而弯矩、剪力影响线是在损伤位置产生突变峰值形式的突变。为了使多类型影响线存在统一的衡量标准,进行D-S证据融合,需要赋予三种信息源相同的属性。因此构建的基本参数以及损伤指标能否适用于三种影响线是该方法成功与否的重点难点之一。可对影响线数据进行标准化、阈值化、中心化、规格化、比重化等多种数据归一化方法,择优选择处理方式,以得到相对可行的三种指标参数,使其具有提取方便,可实现程序操作,指标差异明显,具有可比性的特点。
利用matlab程序自动生成对比向量,比较各指标差异,从中挑选几种差异性比较明显的指标作为损伤指标的参数。例如:
突变尖锐系数λ,即影响线超过0.65倍函数最大值的突变高峰部分的峰值与域宽之比;
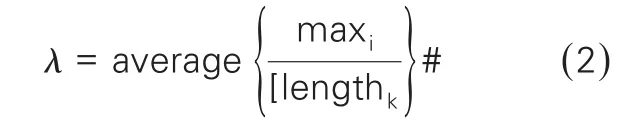
length——使 y≥0.65max的峰值宽度
突变因子数n,即函数超过0.65倍最大值的突变高峰个数;
突变方差s2损伤影响线与原始影响线的差值平方和。
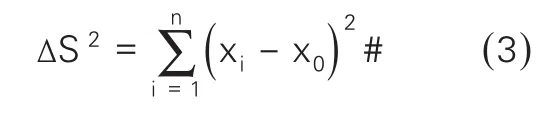
1.4 综合敏感性指标的构建
从这三种参数的定义中,可以看出,突变尖锐系数越大,说明突变峰值差异越大,突变越明显,影响线越敏感;突变因子数越大,说明超过突变阈值的突变峰越多,实际情况下,越有可能被误判,影响线越不敏感;当突变方差越大,说明整条影响线相对于无损状态影响线变化越大,可以从整体反映出变化更明显,更可能得到精确解答,影响线越敏感。通过这三种参数,定义以下影响线敏感性指标K,以此量化影响线对损伤的敏感性:
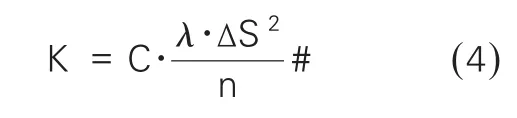
C——定义常数
n——使y≥0.65max的峰值个数
根据以上确定的敏感性系数,提取150条影响线K值;K值越大说明这一类型敏感性越强,在这种损伤工况下更加敏感,识别效果更好,以此,得到150×3的敏感性向量,判断每种损伤工况下敏感性最大的影响线类型,根据以下公式计算最优解情况下,三种属性的三角模糊数:
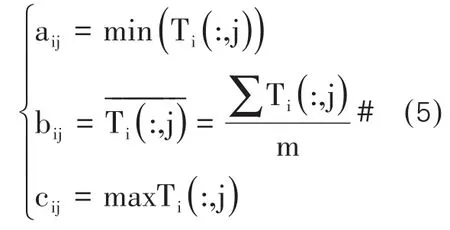
利用Zadeh提出的概念生成相应的隶属度函数,构建属性模型,如下:
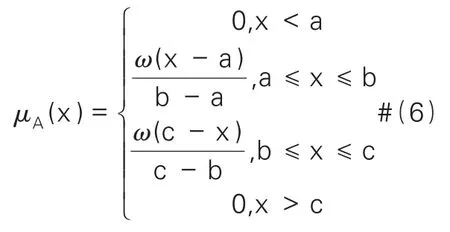
λ
0,n0,ΔS,分别以这三种待测样本属性为横坐标,在属性1、2、3上绘制竖直线,其与构建的三角模糊数模型交点作为对该命题的信任值,当区域为多边形时,以最大值作为顶点,两个最小值作为另外两个点构建新的三角形,直线与该三角形交点纵坐标作为其信任值,即概率分配函数。1.5 D-S证据理论融合
构建信息融合阶段基于D-S证据理论的识别框架,例如:命题S定义为挠度影响线敏感性更高;命题E定义为弯矩影响线敏感性更高;命题V定义为剪力影响线敏感性更高。由此构建了识别框架Θ={S,E,V}。
根据D-S证据理论融合的规则,对三种独立信息源的基本概率指派进行组合合成:
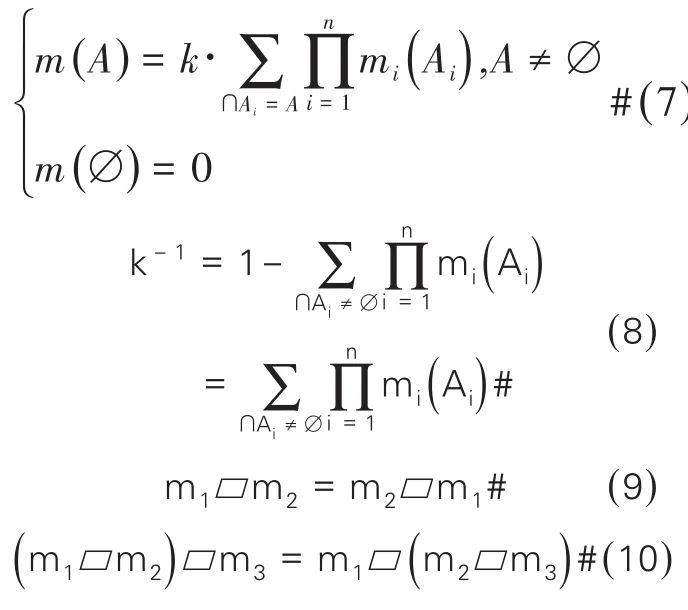
由此得到了融合之后的BPA,将该BPA按照权重分配给三种类型影响线差值函数,为了保证均为正向相加,因此在分配过程中,对差值函数取绝对值。即:
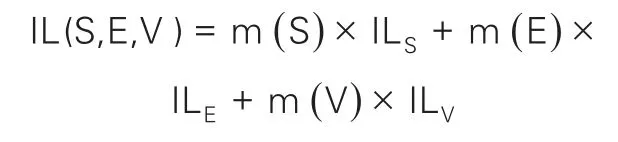
2 核心内容与创新点
2.1 影响线损伤识别方法的敏感性分析
目前国内使用的基于影响线的桥梁损伤识别方法,均通过单一类型的影响线分析。本文创新性地对各种类型影响线进行了不同损伤位置的综合地敏感性分析,着重研究了敏感性规律,解决现有方法在不同工况下的敏感性差异问题,不再局限于单一类型影响线指标,使结果更加全面、准确。
2.2 基于D-S证据理论的信息融合
本项目采用了D-S证据理论算法。融合多源数据,基于D-S证据理论构建损伤指标,通过学科交叉,弥补已有影响线识别方法在未知损伤状态下分析数据的盲目性,为桥梁影响线的融合提供了方法依据。
3 方案不足
3.1 证据冲突
1984 年,Zadeh阐述了 Dempster组合规则的弊端。测试样本输出的基本分配函数可能导致决策出现冲突论证,或者出现指数爆炸现象,使得融合结果出现误差甚至无法继续进行下去,需要进行证据冲突处理。可采用证据关联系数矩阵,利用BPA折扣系数进行信任折扣以得到加权证据。
3.2 模型优化
对于支座位置,为了计算方便,支座节点按无限小模拟,并按理想刚性支座计算,因此在输出影响线时,会使得四个支座位置应力分布过于理想,未考虑材料塑性发展及应力重分布,使影响线差值函数值在支座处为零,与实际不符。
4 深入研究
本文提出的研究方法对象为三种不同类型影响线,单纯考虑了影响线类型对敏感性的影响,而根据分析,影响线的传感器布置位置也会对敏感性造成极大影响,损伤位置越靠近传感器位置,越能产生更大的突变现象,敏感性越大。因此本文的进展融合思路,也可适用于多测点影响线的数据融合,这样对影响线类型、影响线测点进行二次融合可能会得到更好的效果,可以进行下一步研究。
5 结语
本文基于多类型影响线融合的损伤识别方法,提出了一种充分考虑敏感性因素的识别方法。构建不同的敏感性指标来衡量其识别精度,基于此寻找到相应的信息融合方法进行模糊判据,对不同类型影响线进行横向处理、分析、融合,将敏感性因素量化到新的损伤指标中。一定程度地优化现有影响线识别方法,可以使得桥梁检测结果可靠性提高,使桥梁运营期间的安全检测得到保障。
