新加梁、加固梁与现有柱界面受剪性能研究

周伟斌，黄小许 （广州华特建筑结构设计事务所，广东 广州 510640）

0 概述

在既有混凝土结构的改造设计中，新加混凝土梁构件、采用加大截面法加固混凝土梁构件都会在新旧混凝土结构之间形成一个连接界面，从而需要对新旧混凝土结构之间的连接界面进行设计，该连接设计对改造后的结构安全至关重要。新旧混凝土结构之间的连接界面在受弯、受压、受拉方面与整浇混凝土没有本质上的不同，但在受剪方面与之差异较大。因此新旧混凝土连接界面的剪切工作性能和受剪承载力计算成为在既有混凝土结构改造设计中不可回避的一个重要课题。

目前，关于新加梁、加固梁与现有柱界面的受剪性能研究的资料有限，但国内外不少学者对新旧混凝土界面抗剪强度有较为深入的研究。1960年Anderson根据新旧混凝土界面抗剪试验结果，首先提出了新旧混凝土界面抗剪强度计算公式。其后，Birkeland于1966年首次提出了新老混凝土界面的摩擦抗剪理论和抗剪强度计算公式，几十年来该理论经过不断的验证和完善，并已被普遍接受并应用于多个国家设计规范中的界面抗剪强度计算。除了界面的摩擦抗剪理论及计算公式外，国内外根据试验研究结果先后提出了几种不同的计算模型和计算公式，其中Patnaik A H设计制作了8组梁式构件进行试验研究，主要考虑混凝土结合面的粘结强度和纵向钢筋的作用，并根据试验结果提出界面抗剪承载力计算公式。

国内方面，在新老混凝土界面抗剪强度的研究领域做了不少有意义的试验研究工作和分析总结工作，考虑了界面处理方式、混凝土强度、抗剪钢筋数量、界面剂等影响因素，从不同的角度提出了抗剪强度计算公式。其中黄璐、林新鹏等归纳总结了国内外学者基于摩擦抗剪理论、通过对实验结果的分析提出的新旧混凝土界面剪切强度研究成果，收集利用80组试件的实测结果，通过多元非线性回归分析，提出了新旧混凝土界面的抗剪计算公式。

综合来看，国内外对新旧混凝土连接界面在纯剪作用下的抗剪强度研究比较充分，提出了比较成熟的界面抗剪强度计算公式。但在改造工程中新旧混凝土结构之间的连接界面，界面的抗剪钢筋布置形式、弯矩作用等因素都可能对界面抗剪产生决定性影响，目前的试验研究虽然也有涉及各种影响因素，但还只是初步的，还没有足够的试验数据和研究成果为新旧结构连接界面的受剪承载力计算提供支撑。目前梁柱连接的试验数据还很不充分，未能提出合理的界面受剪承载力计算公式，需要对梁柱界面承载力进行系统的试验研究，提出适用于工程实践应用的承载力极限值与设计值计算公式。

1 试验概况

为了研究新旧混凝土界面的滑移变形性能、界面的破坏形态，研究主要参数对梁柱混凝土连接界面抗剪承载力的影响，为连接界面的抗剪设计提供依据而进行本试验。

根据改造工程中新旧混凝土界面的界面状况和受力条件，结合现有试验研究成果，考虑了界面混凝土强度、受拉纵筋、受压纵筋、剪跨比、加固梁类型、荷载布置共六个试件参数设计制作了39个梁柱组合试件，试件分为两批，第一批9组27个试件，第二批2组12个试件，由先浇柱（梁柱）和后浇梁两部分组成，分两阶段制作完成。制作试件时，先浇筑作为支承构件的混凝土柱和被加固梁，然后对原混凝土基面进行凿毛处理，要求在新旧混凝土交接面范围内全表面露出新鲜混凝土，凿毛深度为6mm，形成凹凸均匀的粗糙基面，并用清水和钢丝刷把混凝土凿毛面的粉尘清洗干净；在浇筑新混凝土前，应淋水养护凿毛面不少于12小时，并在新浇筑混凝土前半小时内涂刷水灰比为0.5的水泥浆。梁内纵向钢筋均采用HRB400，植筋时，新加纵筋均植筋锚固于柱内，第一批试件的植入深度取L=15d，第二批试件的植入深度取L=22d，其中d为钢筋直径。最后再新加混凝土梁或者采用加大截面法加固混凝土梁，从而形成现有柱和新加梁、加固梁之间的混凝土连接界面。试件布置图如图1所示，试件参数表如附件表1所示。根据各梁加固方式的差异形成了五种不同的截面形式如图2所示。

部分试件主要试件参数 表1

图1 梁柱组合试件布置示意图

图2 新加梁、加固梁界面类型大样图

在试验中每组试件均预留混凝土试压件，每种规格的纵筋均预留一组3条试拉件。在梁面的每根受拉纵筋上对称粘贴两片应变片，应变片中心位于梁柱混凝土界面位置，用于观测界面处的纵筋应变。在界面两侧安装位移计，用于观测界面的滑移变形。

试件的加载装置图如图3所示，加载装置把混凝土柱固定于试验台上，采用液压加载装置对梁分级施加荷载。集中荷载的加载钢垫板宽度为100mm。试验时观测、记录试件破坏形态、界面初裂荷载、试件破坏荷载、裂缝分布和裂缝宽度、界面剪切滑移变形、界面处受拉纵筋应变、梁的挠度。

图3 梁柱组合试件试验装置图

2 试验结果及分析

观察试验过程及结果后发现大部分试件最后发生界面剪切破坏；有部分试件界面出现剪切开裂、破坏形态接近界面剪切破坏；少数试件界面没有剪切开裂或虽然界面剪切开裂但尚未发生剪切破坏，即试验时破坏荷载尚未达到界面剪切破坏荷载；大部分试件破坏抗剪钢筋已达到或接近屈服；植入深度为15倍直径的部分试件出现了纵筋拔出的现象，而植入深度为22倍直径的试件均未发生纵筋拔出破坏。界面开裂荷载与极限荷载之比为0.14～0.68，大部分试件开裂较早，界面带裂缝工作。由于试件较多，仅列举破坏现象较为典型的几组试件如图4所示，部分试件静载试验的试验结果如表1所示。

图4 部分试件破坏形式

在界面开裂以致界面达到破坏荷载后，由于纵向钢筋的作用，界面滑移变形继续缓慢发展，界面剪切破坏虽属于脆性破坏，但还是具有一定的延性。部分试件的荷载—界面相对滑移曲线如图5所示。

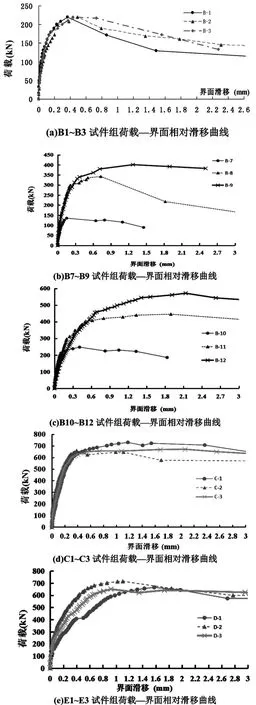
图5 部分试件的荷载—界面相对滑移曲线

3 连接界面的剪切机理

假设界面形成滑移裂缝，剪力作用促使界面两侧混凝土相对滑动，滑移使两侧混凝土产生分离趋势、纵筋受拉直至屈服，钢筋拉力反过来约束混凝土的分离趋势、混凝土在界面上产生压应力，两侧混凝土在剪力作用下形成静摩擦、提供摩擦力，从而阻止界面继续滑移。在界面凿毛的条件下，界面两侧混凝土还具有咬合摩擦力，与静摩擦力共同发挥作用。抗剪钢筋屈服或界面混凝土摩擦破坏，都会导致界面剪切破坏。因此，足够多的界面抗剪钢筋和足够大的界面面积是保证界面不发生剪切破坏的必须同时具备的两个条件。

部分试件静载试验结果 表2

与单纯的剪切界面不同，新旧结构之间的连接界面除符合剪切摩擦模型的受力机理外，还受到其他多种因素的附加影响。这些附加因素主要包括：弯矩的作用使界面上的正应力分布发生改变，甚至出现拉应力区，对界面抗剪不利，弯矩的影响可以用剪跨比来表达；原有梁的整浇界面有利于界面抗剪，整浇界面的不对称布置则会削弱该有利作用；对于包柱式构件，一方面，由于界面抗剪钢筋布置在外侧，界面抗剪钢筋的对界面抗剪承载力的作用稍弱，而另一方面，由于托换构件对界面起四面围箍作用，混凝土界面强度对界面抗剪承载力的作用稍大。

按不同的试验参数，对比分析新旧混凝土连接界面的试验结果，可以发现各种因素与连接界面抗剪承载力的相关性。抗剪承载力和抗剪钢筋（受拉区钢筋）正相关，基本成线性关系，和受压区钢筋无明显相关关系；抗剪承载力和剪跨比显著负相关，反映出弯矩对界面抗剪承载力的不利影响。这种负相关并不成线性关系，随着剪跨比的增大，界面抗剪承载力对剪跨比的敏感程度有所减弱。整浇连接面比新旧混凝土连接界面的抗剪承载力明显要高。在加固梁和柱的连接界面中，原有梁的整浇界面有利于提高整个界面的抗剪承载力。相对于左右对称的梁底加固和三侧加固梁，左右不对称的单侧加固梁中的整浇连接面对整个界面的抗剪承载力贡献比较小。按界面尺寸计算界面抗剪承载力时，试验值较新加梁、加固梁稍高。这可以解释为，由于包柱式构件对混凝土柱的四面围箍作用，对连接界面的约束更为有利，有利于混凝土抗剪强度的发挥。如果界面发生受弯破坏或钢筋锚固破坏，则会影响界面抗剪承载力的发挥。连接界面设计时要充分发挥界面抗剪承载力，必须保证界面不发生受弯破坏或钢筋锚固破坏。

4 连接界面的受剪承载力计算

根据界面剪切机理和各种因素对连接界面受剪承载力的影响程度，在界面抗剪承载力计算公式中，采用按界面抗剪钢筋计算界面受剪承载力、按界面混凝土强度限制受剪承载力上限的表达方式，受剪承载力的计算公式中同时考虑了界面处剪跨比、整浇混凝土界面面积与界面总面积的比值、新加混凝土界面与原整浇混凝土界面对称性三个因素的影响。受压区钢筋的销栓作用、均布荷载的有利作用均在计算受剪承载力时忽略不计。

A1、A2、A3三个整浇对比试件，B4、B7、B10三个锚固破坏试件，F7～F10四个大剪跨受弯破坏试件，共有10个试件的试验结果不参与回归统计。参与回归统计的试件数量为27个。

4.1 受剪承载力极限值计算公式及回归统计分析

连接界面的受剪承载力极限值回归计算公式为：

受剪界面限制条件：

式中：

f

——混凝土的轴心抗压强度，取新、旧混凝土轴心抗压强度的较低值；

A

、

A

——位于受拉区的原整浇混凝土界面内抗剪钢筋、新加混凝土界面内抗剪钢筋的截面面积；

f

、

f

——位于受拉区的原整浇混凝土界面内抗剪钢筋、新加混凝土界面内抗剪钢筋的抗拉屈服强度值；

λ

——连接界面处的名义剪跨比，取

λ

=

M

/

Vh

，

M

为连接界面处与剪力值

V

对应的弯矩值；

γ

——原整浇混凝土界面的受剪承载力提高系数，按原整浇混凝土界面与新加混凝土界面的对称程度取

γ

=0.3～0.6；当原构件单侧加固时取

γ

=0.3；当对原构件两侧对称加固时取

γ

=0.6；

αA

——原整浇混凝土界面面积与加固后总界面面积的比值，

αA

=

A

/

A

A

、

A

——原整浇混凝土界面、加固后总界面的计算面积：

A

=

b

h

、

A

=

bh

；

除了转让子公司或孙公司保壳，卖房卖土地以求留A的上市公司也不在少数，上述*ST椰岛股权转让的同时也搭配出售椰岛综合楼。

b

、

h

——原整浇混凝土界面、加固后总界面的宽度；

h

、

h

——原整浇混凝土界面、加固后总界面的高度。

按公式4.1-1计算试件的界面受剪承载力极限值，回归统计各类试件及全部27个试件的受剪承载力试验值与计算值之比，如表3所示。

试件受剪承载力试验值与计算值之比 表3

定义功能函数Z如下式所示：

式中：

R

——受剪承载力试验值；

S

——设计公式计算值。将表3中的受剪承载力试验值（R）和设计公式计算值（S）均代入公式4.1-3中，计算得到功能函数Z的平均值

μ

=1.04，标准差

σ

=0.259，可靠指标计算值

β

=4.03。27个试件的界面剪切破坏荷载与界面受剪承载力设计值之比见表4，该比值最小为1.60，最大为2.59，即便对于大剪跨未发生界面剪切破坏的构件，计算比值也大于1.55，说明设计公式也可以涵盖大剪跨构件。设计公式的可靠指标计算值

β

=4.03，满足现行国家标准《建筑结构可靠度设计标准》（GB50068-2001）关于安全等级二级、破坏类型为脆性破坏的结构构件承载能力极限状态的可靠

β

≥3.7的可靠度要求，设计公式具有良好的相关性和较高的安全储备。

试件界面剪切破坏荷载与承载力设计值之比 表4

5 设计值计算公式、规范公式与试验值的比较

对于新旧混凝土连接界面的受剪承载力，引用前述的梁柱界面试验结果，与本文提出的界面受剪承载力计算公式、国内外代表性规范计算公式进行比较。对比时采用新加梁和现有柱的界面试验中发生界面剪切滑移破坏的试件参数和试验数据。按照实际的受剪承载力试验情况，对受剪承载力计算公式的适用条件作统一假定：

①连接界面为均匀凿毛的新旧混凝土界面；

②界面钢筋抗剪钢筋垂直于界面；

③轴向力为零。

按此假定本文提出的界面受剪承载力设计值的计算公式：

当

λ

＜5时取

λ

=5计算。

中国标准GB 50010—2010关于叠合面受剪承载力的计算公式：

欧洲规范EN 1992-1-1-2004关于界面抗剪承载力的计算公式：

美国规范ACI318-08关于连接界面的抗剪承载力计算公式：

对比结果列于表5。对于剪跨比为0.3～4.0的新旧混凝土结构连接界面，受剪承载力的计算结果与试验值对比结果如下：

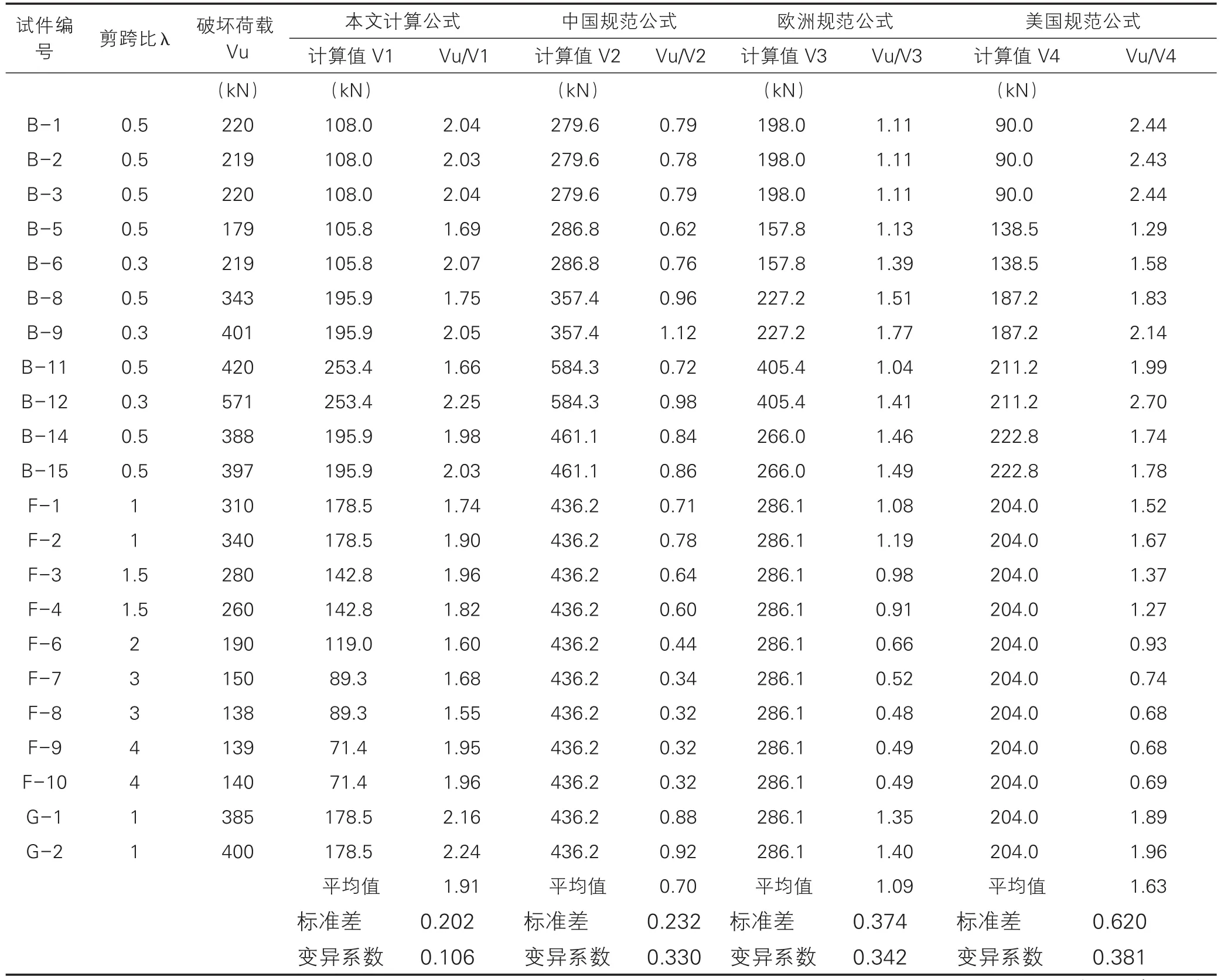
设计值计算公式、规范公式与试验值的比较 表5

①按中国规范和欧洲规范计算时，试验值与计算值之比太小，且数据很离散，计算结果与试验结果不吻合，规范公式不适用于有弯矩作用的情况；

②按美国规范计算时，试验值与计算值之比平均值达到1.63，但总体上离散性太大。按剪跨比大小来区分，在剪跨比不大于1.0时，试验值与计算值之比值较大；而在剪跨比大于1.0时，试验值与计算值之比值太小，大部分甚至小于1.0，计算值明显偏大，规范公式不适用剪跨比较大的情况；

③按本文公式计算时，计算公式考虑了剪跨比的影响，试验值与计算值之比为1.55～2.25，平均值为1.91，标准差为0.202，变异系数为0.106，离散性较小，吻合良好，且具有足够的可靠性；

④本文公式在表达方式上与美国规范公式类似，当接近直剪

λ

≤5时两者比较有可比性。当接近直剪时，本文公式简化为：

而美国规范公式简化为（直剪时界面钢筋均为受拉钢筋）：

两者相比较，本文公式的受剪承载力计算值比美国规范公式要高16%～20%。与11个小剪跨比试件的试验值比较，按美国规范公式计算时，试验值与计算值之比为1.29～2.70，平均值为2.04，标准差为0.436，变异系数为0.214，数据比较离散、相关性较差；按本文公式计算时，试验值与计算值之比为1.66～2.25，平均值为 1.96，标准差为0.183，变异系数为0.093，计算值与试验值相关性较好，与试验结果更加吻合。

6 总结

对新加梁、加固梁与现有柱界面受剪性能研究后，得出以下结论：

①采用混凝土基面凿毛、涂刷纯水泥浆进行界面处理时，连接界面剪切工作性能良好，界面发生剪切滑移破坏属于脆性破坏，但具有一定延性；

②在加固梁与现有柱的连接界面内，其中原有梁的整浇界面有利于提高整个连接界面的抗剪承载力，加大截面相对于原有梁截面越对称，对界面抗剪就越有利；

③凿毛处理的连接界面符合摩擦抗剪机理，在剪力作用下，界面形成滑移裂缝，剪力作用促使界面两侧混凝土相对滑移，滑移使粗糙界面的两侧混凝土产生分离、张开的趋势，横穿界面的纵筋因此受拉、并反过来约束混凝土的分离趋势，从而使混凝土在界面上产生压应力，界面在压应力作用下提供摩擦力、阻止界面继续滑移，形成界面的抗剪能力，按照这一机理，界面抗剪钢筋的抗拉能力决定界面抗剪承载力的大小，但其前提条件是界面上的混凝土具备足够强度、不发生破坏，即界面混凝土强度制约了界面抗剪承载力的上限；

④对于新加梁、加固梁与现有柱之间的连接界面，受剪承载力设计值可以按本文提出的设计值计算公式计算，计算值与试验值具有良好的相关性，可靠指标满足国家规范要求。