双指标阶段性退化建模及可靠性分析
2021-11-29毛泽龙王治华刘成瑞
毛泽龙, 王治华,*, 吴 琼, 刘成瑞
(1. 北京航空航天大学航空科学与工程学院, 北京 100083; 2. 北京空间飞行器总体设计部, 北京 100080;3. 北京控制工程研究所研发中心, 北京 100080)
0 引 言
目前,针对高可靠长寿命产品的可靠性分析,性能退化建模方法已广泛应用。为简化模型,早期研究大多在产品退化过程仅具备单一退化规律的前提下开展。工程实际中,一方面,产品自身物理机理或运行环境、负载情况等的动态变化,会导致退化过程呈现出两阶段甚至多阶段的演变特点[1-3];另一方面,由于功能多样性和组成复杂性,产品往往具有多个性能指标,且这些指标间存在耦合关系[4-6]。此时,单一指标单一阶段的性能退化模型往往不能准确反映高可靠长寿命产品的真实退化规律。针对此类产品,如何建立合理退化模型准确描述多阶段、多指标退化规律成为相关研究的热点和难点。
针对单一指标多阶段性能退化问题,基于随机过程的方法能较好描述退化过程中由产品内部失效机理及外界环境因素导致的时变不确定性,已广泛应用[7]。其中,Wiener过程由于能描述非单调退化过程以及良好的数学性质和物理解释,应用最为普遍[8-9]。文献[10]针对液力耦合器退化过程呈现先慢后快的特征,以振动幅值为性能指标,基于Wiener过程建立了两阶段退化模型。文献[11]针对液力耦合器第一阶段为单调退化,第二阶段为非单调退化的特点,进一步提出了基于Gamma过程和Wiener过程的两阶段退化模型。文献[12]针对电容器容量退化特征,建立三阶段Wiener过程评估其可靠性。针对产品退化过程中存在的非线性规律,文献[13]基于Wiener过程建立了两阶段非线性模型;文献[14]进一步建立了发动机的多阶段非线性退化模型。
针对多指标联合退化问题,指标间相关性的合理描述至关重要。目前考虑指标相关性的建模方法主要有以下几类:基于多维随机过程(如多维Wiener过程)建模[15-18];将多指标融合为单一指标后建模[19-20];基于Copula函数的建模[4,21-29]。其中,基于多维随机过程的建模方法适用于各指标退化规律相近的情况;对于第二种思路,融合原始指标后得到的新指标,难以明确其物理意义及相应失效阈值,限制了其应用范围;而基于Copula函数的建模方法能够有效克服以上问题,因此得到了广泛应用。文献[21]基于Wiener过程和Copula函数建立双指标退化模型,各指标的边缘分布通过Wiener过程描述,指标间的相关关系由Copula函数表征。文献[22]进一步研究退化过程具有个体差异时的双指标建模问题。文献[23]以某型继电器为研究对象,提出了基于Copula函数和Wiener过程的双指标加速退化数据建模方法,并建立了基于贝叶斯马尔可夫链蒙特卡罗的模型参数估计方法,扩充了双指标退化模型的使用范围。文献[4,24-26]进一步针对指标数量更多的情况开展了研究。考虑到某些产品各指标退化过程是单调的,文献[27-28]采用逆高斯过程和Copula函数建立双指标退化模型。
综上可见,以上有关阶段性特征的研究均围绕单一指标的退化过程展开,无法描述多指标联合退化时的情况;有关多指标建模研究均未考虑指标退化的阶段性特征,可能导致可靠度评估结果出现偏差。对于产品退化过程中耦合性与阶段性规律并存时可靠性分析问题有待进一步研究。文献[29]以飞机舱门锁为研究对象,采用指标间相关性描述退化过程的耦合性,对退化过程同时存在耦合性与阶段性的建模问题进行了探究。
本文通过Copula函数描述指标间相关性,引入变点描述退化阶段性,考虑不同阶段指标间耦合性规律变化,建立了双指标阶段性退化模型,并给出了可靠性评估方法。另外,针对退化过程包含两个变点且不在同一位置,而难以估计的问题,提出了一种考虑双指标变点的模型参数整体估计方法。最后,通过实例分析,验证了本文方法的建模合理性与可靠性分析有效性。
1 退化规律分析与模型引出
工程实际中,一些产品退化过程呈现多指标和阶段性规律并存的特点。例如,飞机舱门锁[29]关键部分为连杆机构,连杆之间、连杆与基座间均通过轴和轴套连接,构成了多个连接点。在使用中,连接点轴套会逐渐磨损,当任一连接点轴套磨损量超出对应的失效阈值,则舱门锁失效。通过对舱门锁的失效机理和退化数据分析,发现其中两处连接点轴套的磨损最为严重,将这两处轴套的磨损量作为舱门锁的两个性能指标,记为指标1和指标2,其性能退化测试数据如图1所示。
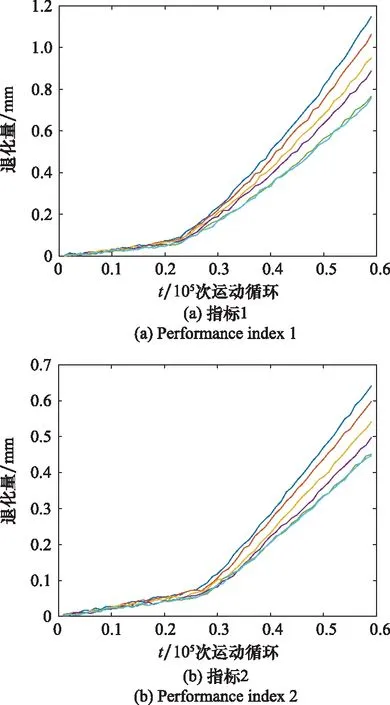
图1 舱门锁性能退化数据Fig.1 Degradation data of cabin door lock mechanism
从图1中可见,指标1和指标2的退化呈现明显的两阶段特征,这是由于前期润滑剂充足,轴与轴套间润滑良好,轴套磨损速率较慢;随着润滑剂消耗,当消耗到某一水平,轴套磨损速率迅速增大。同时需注意,指标1变点在0.2×105次运动循环附近,指标2变点在0.3×105次运动循环附近,两指标变点不在同一位置。此外,由于舱门锁的结构特点,两连接点的磨损也相互影响,即指标1和指标2之间还存在耦合关系。
综上可见,此类产品退化特点可总结如下:考虑产品具有两个性能指标,令Xi(t)表示第i个指标的退化过程,其中i=1,2;当任一指标首次达到对应失效阈值时,则产品发生失效;两指标退化过程均呈现阶段性,且在很多情况下,不同阶段内指标相关性强弱不一致(该结论将在实例分析中说明)。根据两指标变点τ1、τ2间位置关系,问题可分为两类:考虑最一般的情况,当τ1≠τ2时,不妨令τ1<τ2,变点τ1、τ2将产品退化过程分为3段:(0,τ1]、(τ1,τ2]、(τ2,+∞),各段内指标退化规律与耦合规律均可以不相同;当τ1=τ2时,产品退化过程为两阶段,可视为前述一般情况的简化。
此类产品退化过程中耦合性和阶段性规律并存,带来了以下挑战:一是如何建立合理的退化模型表征退化过程中不同阶段双指标间耦合性规律;二是由于产品两指标退化过程均包含变点,且两变点不在同一位置,如何建立有效的模型参数估计方法;最后,由于退化过程复杂,可靠度解析形式难以获得,如何基于退化模型有效评估产品可靠性。
2 双指标阶段性退化建模
2.1 边缘退化建模
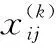
对于两个性能指标均呈现两阶段退化规律的情况,对指标i,基于Wiener过程建立如下两阶段边缘退化模型:
Xi(t)=[μi1Λi1(t)+σi1B(Λi1(t))]I(0,τi](t)+
[Xi(τi)+μi2Λi2(t-τi)+σi2B(Λi2(t-τi))]I(τi,∞)(t)
(1)
式中:τi为指标i的变点(即在时刻τi,指标i退化过程由第一阶段进入第二阶段);μi1和μi2分别为指标i第一和第二阶段的漂移系数,表征各阶段的退化速率;σi1和σi2分别为指标i第一和第二阶段的扩散系数,表征各阶段分散性;I(0,τi](t)、I(τi,∞)(t)为示性函数;B(·)为标准Wiener过程;Λi1(t)=tγi1、Λi2(t-τi)=(t-τi)γi2为第一和第二阶段的时间尺度变换函数,分别表征指标i在各阶段退化的非线性特征;指标i的边缘退化模型参数可记为Θi=(μi1,μi2,σi1,σi2,γi1,γi2,τi),i=1,2。
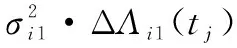
(2)
则退化增量ΔXij在变点τi前后服从不同参数的正态分布可表示为
(3)
退化增量ΔXij的累积分布函数和概率密度函数分别为
(4)
(5)
式中:Φ(·)为标准正态分布的累积分布函数。
2.2 基于Copula的双指标阶段性退化建模
根据常用假设[21],本文通过Copula函数描述指标间的相关性,在不同时间间隔内,指标1与指标2退化增量间的相关性可忽略,即仅考虑同一时间间隔内两指标退化增量间的相关性;由此在边缘退化模型基础上,构建双指标阶段性退化模型。根据Sklar’s理论,两指标退化增量ΔX1j、ΔX2j的联合分布函数F(ΔX1j,ΔX2j)可由各自边缘分布函数F1(ΔX1j)、F2(ΔX2j)和Copula函数表示,即
F(ΔX1j,ΔX2j)=C(F1(ΔX1j),F2(ΔX2j);θ)
(6)
式中:C(·)为Copula函数,表征指标退化增量间的相关关系;θ为Copula函数参数,与指标退化增量间的相关性大小有关。
两指标的变点τ1、τ2将测试时间段分成了3段,考虑到各段内指标间的相关性大小可能不一致,θ在各段内取值也不相同,分别为θ1、θ2、θ3,即
θ=θ1I(0,τ1](tj)+θ2I(τ1,τ2](tj)+θ3I(τ2,∞)(tj)
(7)
针对两个指标的情况,目前应用较广的Copula函数有Gaussian Copula、 Gumbel Copula、Clayton Copula、Frank Copula等,这几种Copula函数具有不同的耦合性描述效果。本文采用在退化领域已广泛使用的Frank Copula函数描述指标增量间的耦合性。Frank Copula函数及其密度函数具体形式见文献[30]。综合考虑指标退化的阶段性与指标间的相关性,建立双指标阶段性退化模型如下:
(8)
模型参数可记为Θ=(Θ1,Θ2,θ1,θ2,θ3)。
3 可靠性分析
确定模型参数估计值是利用双指标阶段性模型进行可靠性分析的前提。模型待估参数为Θ=(Θ1,Θ2,θ1,θ2,θ3)。由于参数较多,难以通过直接优化对数似然函数获得模型参数估计值,且模型参数中包含两个变点,进一步给参数估计带来困难。针对以上问题,本文提出了一种考虑双指标变点的模型参数整体估计方法。
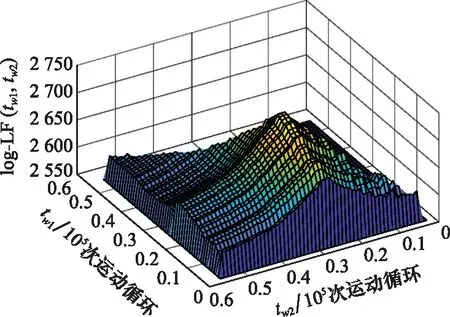
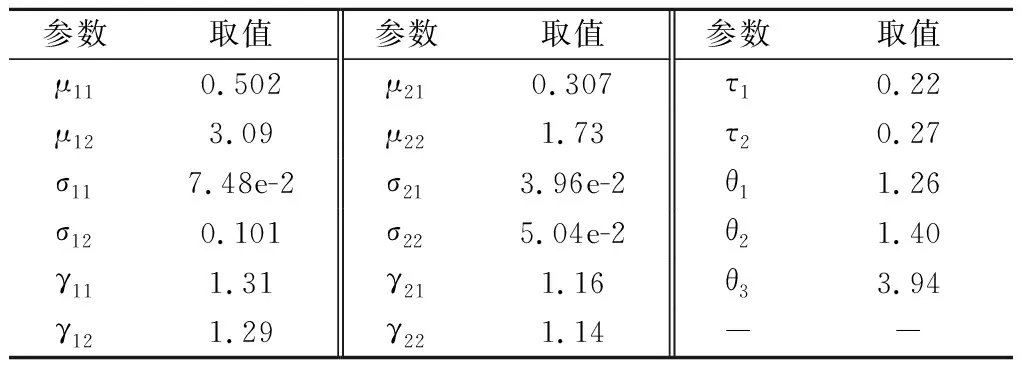
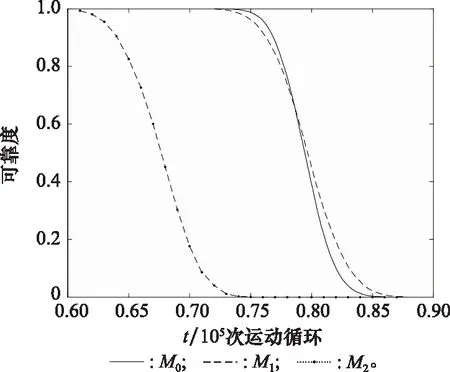
假设两个性能指标的变点τ1、τ2分别位于测试时刻tw1、tw2(tw1 f(ΔX1j,ΔX2j)=c(F1(ΔX1j),F2(ΔX2j);θ)· (9) 式中:c(·)为Frank Copula函数对应的密度函数。 对于(t1,t2,…,tw1)时刻的测试数据,由式(9)得到同一时刻各指标退化增量的联合密度函数为 (10) 进一步由不同时刻退化增量独立,建立(t1,t2,…,tw1)时刻的退化数据的似然函数为 (11) 相应的对数似然函数为 (12) 类似地,(tw1+1,tw1+2,…,tw2)、(tw2+1,tw2+2,…,tn)时刻的测试数据的对数似然函数分别为 (13) (14) 综上,由式(12)~式(14),m个试样在时间段[t1,tn]的对数似然函数可表示为 lnL(Θ)=lnL1+lnL2+lnL3 (15) 建立对数似然函数后,根据以下步骤估计模型参数。 步骤 1定义如下关于tw1、tw2的函数。 log-LF(tw1,tw2)=lnL(Θ)max|τ1=tw1,τ2=tw2 (16) 式中:log-LF(tw1,tw2)为假定变点τ1、τ2位于测试时刻tw1、tw2时,对数似然函数lnL(Θ)的最大值。其中对lnL(Θ)的优化基于遗传算法实现,本文通过调用Matlab工具箱的ga函数优化lnL(Θ)。 步骤 2确定tw1、tw2可能的取值组合。由于tw1、tw2满足t1 步骤 3计算函数log-LF(tw1,tw2)在上述取值组合对应的值。取log-LF(tw1,tw2)最大时对应的取值组合作为变点估计值,对应的其他模型参数取值作为模型参数最优估计。 得到模型参数估计值后,可结合退化模型及失效阈值计算产品可靠度。对于两指标联合退化的产品,当其任一指标退化量首次达到失效阈值时,即认为其发生失效。具体地,设产品两指标对应失效阈值分别为D1、D2,产品可靠度可定义如下: (17) 由于产品退化过程复杂,可靠度的解析形式难以获得,采用蒙特卡罗方法计算可靠度。蒙特卡罗方法的基本思想是应用随机抽样技术得到符合待求解分布的样本,通过对样本值的观察与统计,实现对未知分布的分析。 根据双指标阶段性退化模型及模型参数估计值,开展蒙特卡罗仿真,生成样本容量为N的仿真退化数据;统计各样本失效时间Th,其中h=1,2,…,N;统计t时刻未失效样本个数N′(t),即满足Th>t的样本个数,则t时刻可靠度为R(t)=N′(t)/N。其中,生成仿真数据具体包括以下步骤。 步骤 1设定仿真时间和步长等参数,为了确保仿真样本在仿真期间发生失效,仿真时间应尽量长一些。设仿真时间步长为Δt,仿真时刻数为M,则总仿真时长为MΔt。 步骤 2从退化增量联合分布C(F1(ΔX1j),F2(ΔX2j);θ)生成仿真时间段[(s-1)Δt,sΔt]内指标退化增量[ΔX1(sΔt),ΔX2(sΔt)]T,其中s=1,2,…,M。 步骤 3重复步骤2,得到仿真时长内,各指标仿真退化增量,记为 步骤 4对退化增量求和得到仿真样本在各仿真时刻指标退化量: 步骤 5重复步骤2~步骤4即可得到样本容量为N的仿真退化数据。 为了验证本文方法的有效性,采用该方法针对舱门锁实例开展分析。将本文模型记为M0,如式(8)所示。为体现本文方法适用性,与如下两种参考方法进行对比:① 现有仅考虑指标间耦合性的双指标模型,记为M1,模型具体形式见文献[21],以说明在双指标退化中考虑阶段性的意义;② 实例数据来源于文献[29],该文献针对舱门锁的退化特点建立了一种分析方法,将文献[29]方法记为M2。 采用本文模型对舱门锁性能退化数据进行退化建模和参数估计,得到对数似然函数log-LF(tw1,tw2)随变点tw1、tw2变化关系如图2所示。 图2 log-LF(tw1,tw2)随变点变化图Fig.2 log-LF(tw1, tw2) variation with change points tw1 and tw2 表1 本文方法M0参数估计结果 由表1可见,不论对于指标1还是指标2,第一、二阶段模型参数都有明显差异,说明同一指标不同阶段退化速率及分散性规律发生变化;此外,不同阶段Copula参数的不同说明不同阶段指标间相关性规律存在差异。 为了对比各模型拟合效果,表2列出了3种模型的对数似然函数值和AIC(akaike information criterion)值。其中AIC值定义如下: AIC=-2(log-LF)+2n′ (18) 式中:n′为未知模型参数个数。AIC值越小,模型拟合能力更优。 表2 log-LF值和AIC值对比结果 由表2可见,本文模型M0的log-LF和AIC值均优于参考模型,这是由于本文方法同时考虑产品退化过程中的阶段性与相关性规律,能够合理描述退化过程。 为了更为直观说明3种模型拟合效果及参数估计准确性,图3给出了平均退化曲线对比结果。从图3中可知,对于指标1和指标2,本文方法M0给出的平均退化曲线能够有效描述样本均值的变化规律。 图3 平均退化曲线对比结果Fig.3 Comparision results of mean degradation curves 进一步,基于M0、M1和M2对舱门锁进行可靠性评估。指标1和指标2失效阈值分别为D1=1.6、D2=0.9。图4展示了基于各模型得到的产品可靠度曲线,可见相较于本文模型M0,仅考虑两指标耦合性的模型M1前期结果偏保守,后期结果偏危险;模型M2得到的可靠性评估结果最为保守。 图4 可靠度曲线对比结果Fig.4 Comparative results of reliability curves 通过以上对比说明本实例中,当产品具有双指标联合、阶段性退化特点时,须综合考虑两方面特点进行合理建模,方能开展有效的可靠性分析。 针对产品同时具有双指标耦合性与阶段性退化规律,本文提出了一种双指标阶段性退化模型,并建立了可靠性分析方法。针对两指标变点不在同一位置的一般情况,本文建立了一种考虑双指标变点的模型参数整体估计方法。通过实例分析,验证本文方法的有效性。结论如下: (1) 双指标耦合退化且存在阶段性规律时,不同阶段指标间的耦合性强弱可能不一致,建立退化模型时应予以考虑; (2) 本文方法能有效表征退化过程中两指标的耦合性与阶段性规律,可靠性评估结果更为准确可信,符合工程实际需求。
f1(ΔX1j)·f2(ΔX2j)4 实例分析
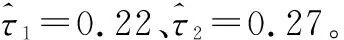


5 结 论
