δ-广义标签多伯努利滤波算法的非线性扩展
2021-11-29齐美彬胡晶晶程佩琳靳学明
齐美彬, 胡晶晶,*, 程佩琳, 靳学明
(1. 合肥工业大学计算机与信息学院, 安徽 合肥 230009; 2. 中国电子科技集团第38研究所, 安徽 合肥 230088)
0 引 言
多目标跟踪的任务是利用传感器提供的量测数据联合估计目标数量及其状态,而这些量测数据通常受到杂波(噪声)、漏检、虚警等因素的影响,为多目标跟踪的实现带来巨大挑战。目前实现多目标跟踪的方法主要分为:联合概率数据关联(joint probabilistic data association,JPDA)[1-3]、多假设跟踪(multiple hypothesis tracking,MHT)[4-6]和随机有限集(random finite set,RFS)[7]。其中RFS方法可以避免执行传统多目标跟踪方法所需的数据关联,成为当前解决多目标跟踪问题的研究热点。其核心是贝叶斯多目标滤波器,采用预测和更新循环迭代计算目标的真实状态,其三大近似算法分别是概率假设密度(probability hypothesis density,PHD)、势PHD(cardinalized PHD,CPHD)和多目标多伯努利(multi-target multi-Bernoulli,MeMBer)滤波器。然而都不能严格地称为多目标滤波器,因为其得到的目标是无标签的,仍不可区分。文献[8-11]引入标签随机有限集的概念解决目标轨迹及唯一性的问题,提出广义标签多伯努利(generalized labeled multi-Bernoulli,GLMB)滤波器及其快速实现(δ-GLMB),并得到广泛应用[12-14]。
随后很多研究学者提出δ-GLMB滤波器的改进算法。这些改进的多目标跟踪方法假设量测噪声协方差先验信息是已知的,但是在很多场景中量测噪声协方差是未知且时刻变化的。针对这个问题,研究者引入了变分贝叶斯(variational Bayesian, VB)方法[15]。文献[15]通过定义未知噪声方差参数的共轭先验分布,用VB近似方法分解固定形式分布和构造递归表达式来逼近线性高斯系统的状态估计,解决未知量测噪声协方差的问题。文献[16-17]针对量测噪声协方差未知的多目标跟踪模型,提出了一种基于VB近似的自适应噪声协方差PHD滤波。文献[18]基于基数平衡多目标多伯努利滤波和VB逼近技术提出了一种VB近似的自适应噪声协方差势均衡MeMBer(cardinality balanced MeMBer,CBMeMBer)滤波。文献[19]在δ-GLMB滤波框架中引入VB近似方法,所提自适应VB-δ-GLMB滤波算法针对未知量测噪声场景下的多目标跟踪具有很强鲁棒性。
上述方法采用高斯混合方式实现,适用于线性运动模型的多目标跟踪,在非线性场景下跟踪性能较低。针对这个问题,本文提出一种适用于非线性模型的临近点容积卡尔曼VB-δ-GLMB滤波算法(简称为PCKF-VB-δ-GLMB)。该算法以高斯实现的VB-δ-GLMB滤波器为基础,将量测噪声和目标状态分布表示为逆伽马和高斯乘积混合形式,结合基于临近点算法和VB的迭代优化与容积卡尔曼滤波提出一种迭代优化容积卡尔曼方法(简称为PCKF-VB),并用该方法对高斯参量进行预测更新,最后为提高滤波精度进行变分贝叶斯容积RTS(VB cubature Rauch-Tung-Striebel)平滑。仿真结果表明本文算法能有效实现非线性系统下多目标跟踪,其性能与现有VB-δ-GLMB跟踪算法相比有明显提高。
1 δ-GLMB滤波算法
1.1 VB近似的非线性滤波
对于量测噪声协方差未知的非线性目标跟踪系统,目标状态方程和量测方程为
xk=f(xk-1)+wk-1
(1)
zk=h(xk)+vk
(2)
式中:xk和zk表示目标状态和量测值;f(·)和h(·)表示状态转移和非线性量测函数;过程噪声wk~N(0,Qk);量测噪声vk~N(0,Rk)。假设目标状态xk和量测噪声协方差Rk模型相互独立,则预测和更新后验密度函数分别由Chapman-Kolmogorov方程和贝叶斯规则给出:
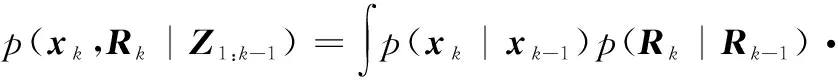
(3)
(4)
式中:Z1:k={z1,z2,…,zk},由于Rk未知,式(4)无法得到解析解,因此引入VB近似来逼近后验密度函数[20],更新联合后验密度可以近似为
p(xk,Rk|Z1:k)≈Qx(xk)QR(Rk)
(5)
通过最小化近似后验密度和真实后验密度之间的KL(Kullback-Leibler)散度来确定近似后验密度:

(6)
当假设目标状态为高斯分布,噪声协方差为逆伽马分布[15]时,近似后验密度为
Qx(xk)=N(xk;mk,Pk)
(7)
(8)
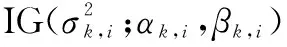
αk|k-1,i=ρiαk-1,i
(9)
βk|k-1,i=ρiβk-1,i
(10)
退化因子ρi∈(0,1],参数更新估计通过定点迭代法[20]获得
(11)
(12)
式中:符号(·)i和(·)ii的含义是向量的第i个元素和矩阵的第i个对角元素;Hk为雅克比矩阵。量测噪声协方差Rk的估计表示为
1.2 标签随机有限集与δ-GLMB
随机有限集是元素和元素的个数均为随机变量的集合,集合中元素的个数称为集合的势。标签RFS在RFS的基础上为集合中的每个元素x∈X都被分配了相应的标签l∈L,即每个目标状态用(x,l)表示,其中l=(k,i),索引i可以区分同一时刻不同目标。

(13)
标准δ-GLMB多目标密度先验分布有如下形式:
(14)

步骤 1预测
(15)
式中:
L+=L∪B

式中:B为新生标签空间;f(x|·,l)为转移密度函数;pB(x,l)为新生目标的状态空间密度函数;pS(·,l)为目标存活概率。
步骤 2更新
(16)
式中:


式中:Z为量测集合;θ表示目标轨迹到量测的映射关系:L→Z,所有映射关系的集合Θ称为关联映射空间;pD(x,l)为检测概率,g(z|x,l)为量测似然函数;κ表示量测生成过程中的杂波密度。
2 PCKF-VB-δ-GLMB滤波算法
为解决未知量测噪声协方差的问题,高斯混合实现的VB-δ-GLMB算法提出用VB近似迭代估计量测噪声协方差和多目标状态联合后验密度。但是该算法仅适用于线性模型的多目标跟踪场景,在非线性场景下跟踪性能较低,因此可以将高斯混合实现的VB-δ-GLMB算法与非线性滤波器结合来实现非线性模型下多目标跟踪。
2.1 PCKF变分近似
用VB方法处理非线性滤波问题[21]时,可以将后验概率密度p(xk|zk)用一个易于计算的概率密度q(xk|θk)来近似。二者间差异可以用KL散度来度量,KL散度越小表示越接近,KL散度表示为

(17)
式中:q(xk|θk)为假设的高斯分布,其参数θk=(xk|k,Pk|k)。L(θk)为变分证据下界(evidence lower bound, ELBO):

(18)


(19)


(20)

(21)
(22)

在过程噪声和量测噪声为高斯假设时,维数同为d的变分分布q(xk|θk)~N(xk|xk|k,Pk|k)和p(xk)~N(xk|xk|k-1,Pk|k-1),因此式(18)展开为
(23)
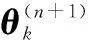
(24)
(25)
本文将基于临近点算法和VB的迭代优化与容积卡尔曼滤波(cubature Kalman filtering, CKF)结合,提出变分逼近的PCKF算法。该算法在传统CKF[25]的更新步骤中结合临近点算法与VB近似进行迭代优化,具体步骤如下。
步骤 1输入初始状态x0和初始协方差矩阵P0。
步骤 2时间更新
(26)
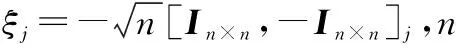
(27)
(28)
量测噪声动态模型参数预测值由式(9)和式(10)得出。
步骤 3量测更新
(29)
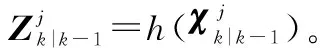
(30)
(31)

(32)
(33)
(34)
(35)
(36)
(37)


因此为解决非线性场景下多目标跟踪问题,可以将非线性滤波方法PCKF-VB与VB-δ-GLMB结合,形成PCKF-VB-δ-GLMB多目标跟踪算法。
2.2 PCKF-VB-δ-GLMB的高斯实现
针对非线性高斯多目标模型预测与更新步骤中带有有限集积分运算而无法求得解析解的问题[26],PCKF-VB-δ-GLMB滤波算法用多个高斯项加权求和的方式,代替传递的伯努利参数来获得闭合解。新生目标为标签多伯努利模型,概率密度函数如下所示:
(38)
式中:J(ξ)为高斯项个数。则基于PCKF-VB-δ-GLMB滤波算法的高斯混合(Gaussian mixture,GM)[27]实现具体步骤如下。
步骤 1预测
假设多目标密度函数π(X)如式(14)形式,其中用高斯和逆伽马积混合形式表示单目标密度p(ξ),表示如下:
(39)
则预测多目标密度π+(X)如式(15)形式,其中预测单目标密度函数为
(40)
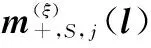
步骤 2更新
假设多目标预测密度π+(X)如式(15)形式,其中单目标密度函数为
综上所述,分析英美文学在英语教学的重要性是非常必要的。世界间的交际来往愈来愈多,英语也越发重要,而将英美文学引入课堂中可以有效地促进学生的英语学习效率,使其能接触到最地道的英语,还能体会到当时当地的风俗文化。英语教学模式应如何引入文学教学有待进一步的探讨。希望本文能为当前的相关研究起到借鉴作用。
(41)
量测为Z,则多目标更新密度如式(16)所示,其中单目标密度函数为
(42)

步骤 3修剪和截断
对于预测更新步骤得到的高斯-逆伽马分量,设置剪枝阈值;修剪权重低于指定剪枝阈值的分量,并将高斯总个数控制在最大限度内。
步骤 4目标个数及目标状态估计
目标个数从势分布中由最大后验估计方法得出;通过最佳基数提取状态估计,从具有与映射基数估计相同基数的所有分量中选取最高权重分量,提取其标签和均值。
2.3 VB-CRTS平滑
为了改善滤波效果,可通过平滑对状态向量做进一步处理,以此提高精度。CRTS平滑算法基于三阶球面-径向容积规则,是高斯平滑范畴内的一种平滑算法[28-29],由前向滤波和逆向平滑两部分组成。对于一般的CRTS平滑算法,量测噪声协方差为常数,不适应实际情况。对于上述非线性模型,结合CRTS平滑算法和VB估计方法,采用VB-CRTS平滑算法实现量测噪声协方差的自适应估计。式(21)和式(22)、式(26)~式(37)组成VB-CRTS前向滤波过程,逆向平滑过程算法如下。
(43)
(2) 平滑增益:
Gk=Dk(Pk|k-1)-1
(44)
(3) 平滑后均值与协方差:
(45)
(46)
3 仿真分析
为更好地仿真机动目标运动状态,本实验采用匀速直线(constant velocity,CV)运动模型和协同转弯(cooperative turning,CT)运动模型来对目标进行建模。在该场景下,我们采用VB-δ-GLMB、本文提出的PCKF-VB-δ-GLMB及其二者分别通过VB-CRTS平滑得到的4种滤波器来实现多目标跟踪,并综合比较性能。
3.1 实验场景设置


表1 不同目标初始状态及起始结束时刻
仿真中目标的运动方程如式(1)和式(2)所示,其中:

3.2 仿真结果与分析
仿真共设置10个目标,目标真实运动轨迹和估计轨迹如图1所示,○和△分别表示起始位置和结束位置,x轴和y轴分别为二维平面内的水平位置和竖直位置。图1中黑色轨迹为机动目标真实运动轨迹,从图中可以看出目标轨迹出现交叉,目标量测混合会导致难以区分。本文算法对机动目标的跟踪效果如图1中红色轨迹所示,图中目标估计轨迹与目标真实运动轨迹几乎重合,因此本文提出滤波器的能准确地实现多目标运动轨迹的估计。

图1 真实运动轨迹与估计轨迹Fig.1 Target tracks and estimated tracks
图2表示上述4种滤波算法的单次势估计与平均势估计。图2(a)为随机抽取的单次蒙特卡罗实验的势估计,从图中可以看出本文提出算法估计的目标数目更加接近实际目标数目。单次实验计算量小,减少目标跟踪的时间,但是不能消除数据随机性。图2(b)为100次蒙特卡罗实验的平均势估计。


图2 势估计Fig.2 Cardinality estimation
本实验采用最优子模式分配(optimal subpattern assignment,OSPA)距离[30]作为评价算法性能的准则指标。OSPA距离综合考虑目标数目估计和目标位置估计,其值越大表明算法的综合精度越差,维数分别为m、n的集合X和Y之间的OSPA距离定义为

(47)
实验中设置距离敏感参数p=2,水平调节参数c=100。图3为4种滤波算法对多目标估计的OSPA距离(见图3(a))和OSPA势估计分量(见图3(b))。观察图3(a)和图3(b)可以看出k=0,10,20时刻OSPA距离和OSPA势估计出现峰值,这是由于目标新生时刻存在概率低,算法不能立刻跟踪到目标;k=80,90时刻OSPA距离和OSPA势估计较大,这是因为目标数目发生变化的时刻算法反应速度延迟时间较长。

图3 OSPA距离与OSPA势估计Fig.3 OSPA distance and cardinality estimation
为减少数据随机性,本文进行100次蒙特卡罗仿真实验,4种滤波器OSPA距离和OSPA势估计如表2所示(重复5组实验取均值,结果保留4位有效数字)。从表2中数据可以看出,对比现有的VB-δ-GLMB算法,本文提出的PCKF-VB-δ-GLMB算法在OSPA距离和OSPA势估计上都有显著改进。其中OSPA距离减少了13.59%,OSPA势估计减少了12.34%,验证了本文提出算法采用PCKF-VB进行预测更新,可以更好地适应非线性多目标跟踪场景。此外,加入VB-CRTS平滑之后,VB-δ-GLMB算法在OSPA距离和OSPA势估计上分别减少了40.96%和12.97%,PCKF-VB-δ-GLMB算法在OSPA距离和OSPA势估计上分别减少了38.74%和16.18%。仿真结果表明VB-CRTS平滑对不同滤波算法均带来了显著改进。

表2 100次仿真的平均性能
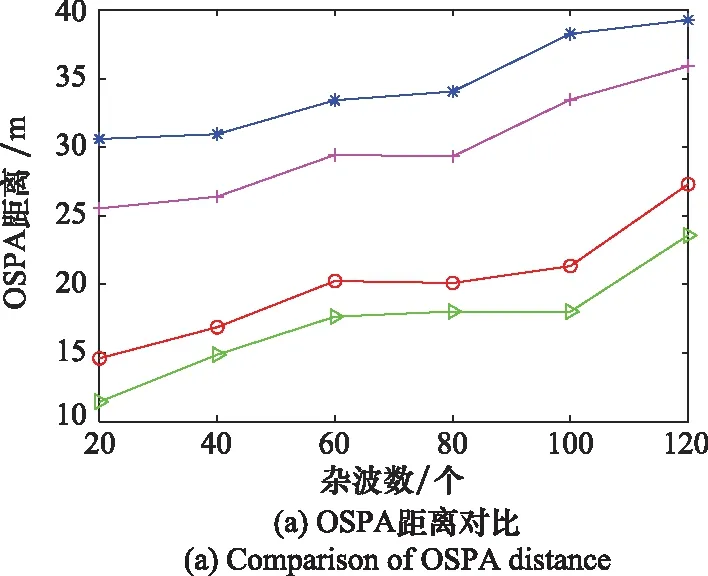
为进一步验证本文提出算法的有效性,在不同杂波数条件下进行100次蒙特卡罗实验,综合比较4种滤波算法的OSPA距离和OSPA势估计。分析图4可以得到以下结论:首先,随着杂波数增多,上述4种滤波算法的OSPA距离和OSPA势估计都随之增大,目标跟踪性能降低;其次,在相同的杂波密度条件下,本文所提算法的OSPA距离和OSPA势估计均小于现有的VB-δ-GLMB算法。
4 结 论
针对高斯实现的VB-δ-GLMB算法在非线性场景下跟踪性能较低的问题,本文提出一种适用于非线性系统的PCKF-VB-δ-GLMB滤波算法。该算法将联合后验分布表示为高斯-逆伽马混合分布,利用PCKF-VB方法对VB-δ-GLMB滤波算法中的高斯参量进行预测更新,最后进行VB-CRTS平滑。仿真结果表明对量测噪声未知的非线性系统,该算法能准确估计目标运动状态与轨迹,多目标跟踪精度得到显著提高。
