一种空间目标三维激光点云与可见光图像重建点云融合方法
2021-11-29张泽旭袁萌萌徐田来邓涵之
苏 宇,张泽旭,袁萌萌,徐田来,邓涵之,王 静
(1. 哈尔滨工业大学 航天学院, 哈尔滨 150001;2. 济南大学 自动化与电气工程学院, 济南 250022;3. 光辐射国防重点实验室, 北京 100085)
引 言
空间在轨服务中获取目标的三维结构与尺寸信息对后续的对接、维护与抓捕等任务具有重要的意义。目标三维结构的获取方法通常有3种途径:一是利用导航相机采集的可见光图像序列进行点云三维重建,点云重建密度和精度较高,但易受到空间环境光照的影响;二是利用激光雷达对目标进行扫描,将不同角度的扫描点云拼接重建,虽然空间光照对重建点云影响较小,但受到激光雷达功率与扫描约束,点云的分辨率较低,同时空间目标的运动会带来很大的误差;三是利用可见光导航相机的重建点云与激光雷达的扫描点云进行深度融合,充分结合两种传感器的优势,这种方法越来越得到学术界关注[1-2]。本文探索一种高精度的三维激光点云与可见光图像重建点云融合方法。
文献[3]利用可见光图像进行三维重建,通过使用连续帧之间的光流来跟踪Harris图像点,并基于双目立体视觉模型生成三维点云,然后将成功跟踪的三维点云利用ICP算法实现目标模型的三维重建。此方法的准确性非常依赖光照条件与图像拍摄效果。
文献[4]利用一个激光传感器和一个线阵CCD同步扫描进行三维重建,通过使每一行激光采样点对应一行可见光采样点,直接实现了激光与可见光采样点的行配准,此方法虽然配准精度较高,但需要目标保持静止,且功耗较高,对追踪航天器提出较高要求,难以应用于空间目标探测。
在点云融合算法方面,大多数研究围绕着对ICP算法进行改进,文献[5-6]提出了一种遗传算法与最小二乘法结合的配准方法。此配准方法收敛性较好,但当点云数据的数据量较大时,其配准精度较差。
文献[7]采用径向基函数[8]的方法首先对模型进行变形,减弱局部大变形对匹配结果的影响,实现形状最佳匹配,此方法较为依赖于经验选择基函数的参数。
除ICP配准算法外,文献[9]提出了运用曲面的特性进行几何曲面匹配的算法,该算法通过计算两个感兴趣表面之间的距离寻找它们之间的最小非刚性变换。
本文首先给出了量纲不同的两组点云的配准融合步骤,给出目标函数表达式,然后提出了一种基于形心的平移矩阵初值确定方法和基于序列图像三维重建反演相机姿态的旋转矩阵初值确定方法,在配准过程中,利用欧式距离判断方法去除边缘杂点,使得融合后的点云更加完整,准确性更高,具体过程如图1所示。

图1 激光点云与可见光图像重建点云ICP融合Fig. 1 Laser point cloud and visible light image reconstruction point cloud ICP fusion

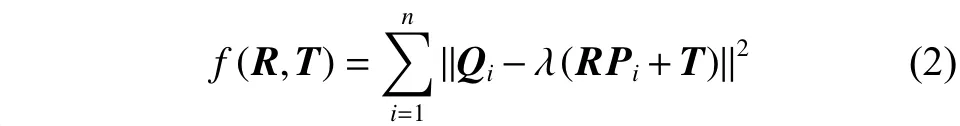
将式(2)作为目标函数,此时只需要先将两组点云放到同一坐标系下(坐标不变),并控制目标函数[10]最小即可。
具体配准步骤[11-12]如下:
2)利用最小二乘法重复选择对应点对,并计算最优刚体变换将不同坐标系下点云数据合并到同一坐标系中,求得使上述对应点对平均距离最小的刚体变换,得到新的和。
4)如果新的变换点集与参考点集满足式(3)要求,即两点集的平均距离小于某一给定阈值,则停止迭代计算,否则新的变换点集作为新的点集继续迭代。

1 配准初值确定方法
ICP算法对运算初值的选取要求严格,初值准确可大大减少迭代次数,提升配准精度,若初值选择不合适,就会使迭代不能收敛到全局最优配准结果,造成匹配失败[13]。
对此,本文选择通过对点云特性及其来源分析,确定配准初值。
1.1 平移矩阵初值确定
对于平移矩阵初值的选取,本文选择针对两种重建点云求取形心的方式获得,具体方式如下。

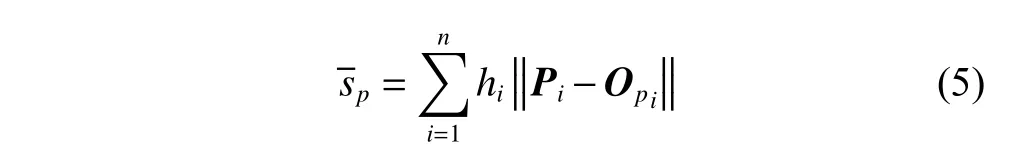
利用两组点云的坐标差作为平移矩阵初值应用于点云配准

1.2 旋转矩阵初值确定
对于坐标系不同的两组点云,本文在确定旋转矩阵初值时,利用序列图像三维重建过程中的基础矩阵的求解进行反演相机相机姿态的计算[14-15],其确定方法如图2所示。
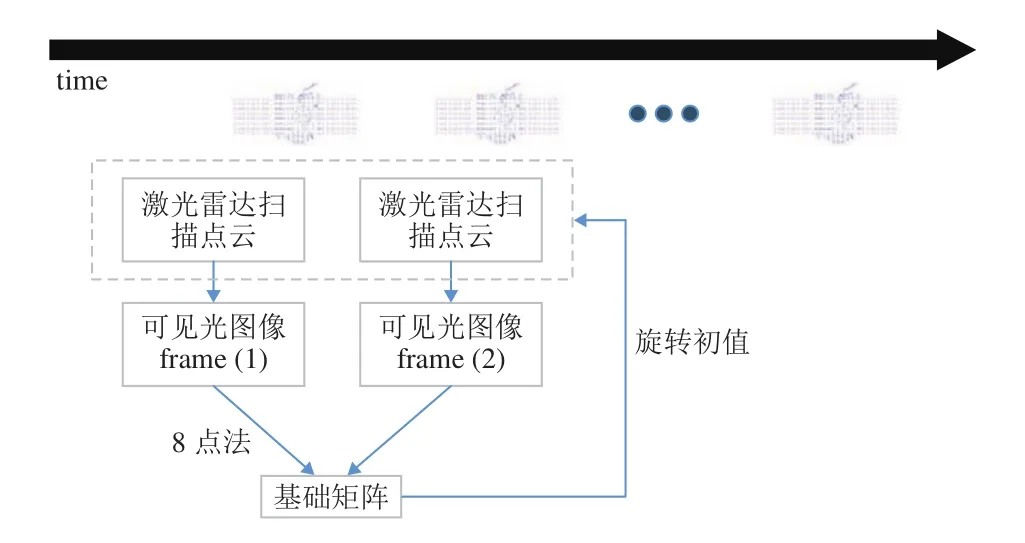
图2 旋转初值确定方法Fig. 2 A method to determine the initial value of rotation


得到对应点如下
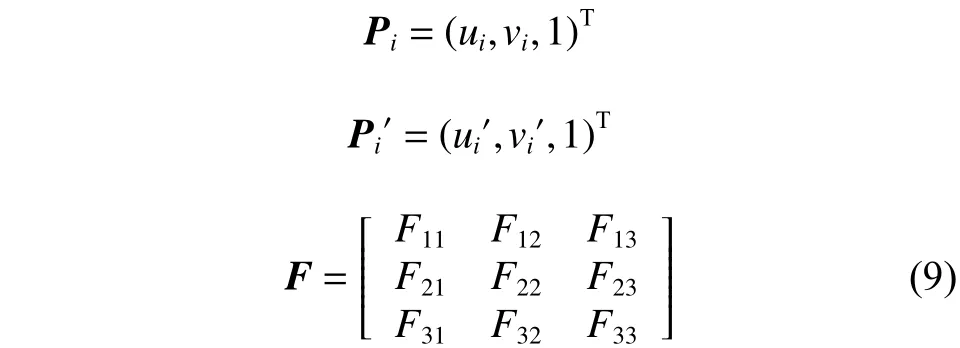
将上述方程展开可得到
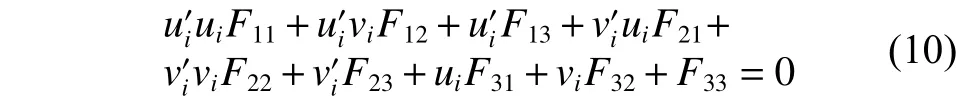
向量构造:
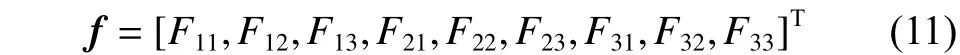
矩阵构造:



由于空间非合作目标序列图像重建中,可见光相机都是事先标定好的,且已知相机内参矩阵为,可利用


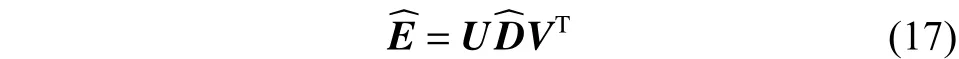


2 基于欧氏距离的融合点云优化
通过上述点云配准过程,可获得两组点云间的最优转换关系。
由于可见光图像三维重建点云解算误差及稠密化过程,导致边缘杂点较多,此时可利用激光雷达扫描点云的点云分布均匀且边缘特性较好的优势,删除可见光图像三维重建点云中的杂点与错误点,具体方法如下。设配准后的对应点集和Q ,对中的一个点,搜索
3 仿真实验与分析
为验证多模数据融合的空间非合作目标三维重建方法,本文利用3Dmax仿真模型进行序列图像的渲染,其获取图像如图3所示。

图3 仿真序列可见光图像Fig. 3 Simulation sequence visible light images
利用SFM原理进行稀疏点云三维重建[21],并利用CMVS进行点云稠密化[22],获得可见光图像的三维重建点云数据,如图4所示。

图4 可见光图像三维重建点云Fig. 4 Visible light image 3D reconstruction point cloud
激光仿真数据选择利用blender进行激光扫描点云仿真,仿真参数如表1所示。

表1 激光扫描点云参数Table 1 Laser scanning point cloud parameters
本文选择在5角度(0°,72°,144°,216°,288°)进行扫描,由于仿真时已知5角度激光雷达的相对位姿及坐标系,可直接将5组点云按对应的转换关系转换到同一坐标系下,结果如图5所示。
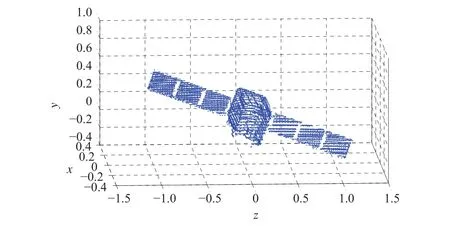
图5 激光扫描三维点云重建结果Fig. 5 Laser scanning 3D point cloud reconstruction results
利用第3部分所述方法进行改进的ICP点云数据融合并剔除边缘杂点,对配准过程中的迭代次数及其对应误差进行记录,获得的最终融合点云如图6和图7所示。
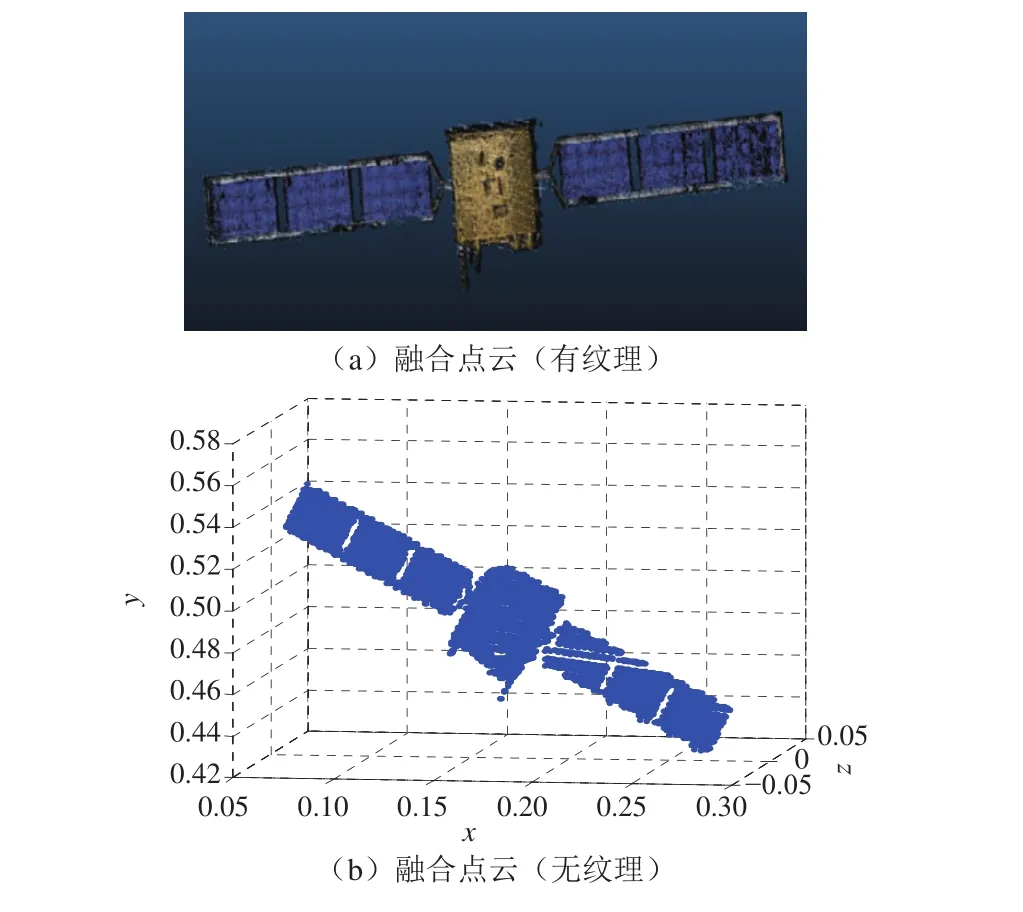
图6 融合后三维点云Fig. 6 3D point cloud after fusion

图7 局部漏洞填补情况Fig. 7 Partial loophole filling result
下面利用融合前后的目标三维点云分别计算目标的尺寸信息,并与实际模型尺寸比较得到的主体尺寸误差率、点云均方差、点云密度(仿真模型总表面积约为21.4 m2),如表2所示。

表2 融合前后各参数对比Table 2 Comparison of parameters before and after fusion
除合成的模型外,本文使用了某卫星模型进行了图像与激光点云仿真,仿真结果如图8所示,分别对图像与激光点云进行重建与点云配准实验,最终获得的合成点云如图9所示。

图8 仿真图像与激光点云Fig. 8 Simulation image and the laser point cloud

图9 点云融合结果Fig. 9 Point cloud fusion result
通过表3和表4中的数据对比可以发现融合点云具有更好的完整性,且精度在融合前后较为稳定,融合效率较高,可为后续任务提供更加可靠的融合点云。

表3 融合前后各参数对比Table 3 Comparison of parameters before and after fusion
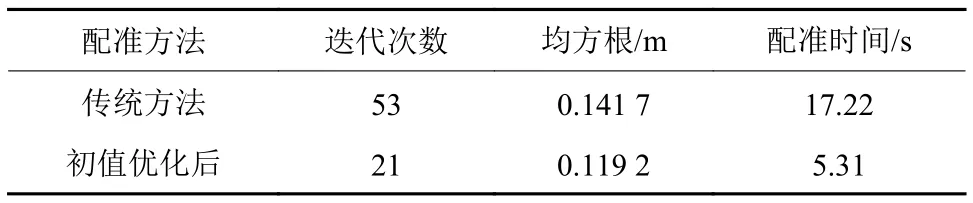
表4 优化前后配准对比Table 4 Registration comparison before and after optimization
4 结 论
基于可见光图像序列的三维重构方法能够得到较为稠密的点云,但是受光照条件影响,点云模型存在较多空洞或缺损,点云重构误差较大,基于激光雷达的重构出的点云较完整,而且点云具有真实尺度信息,但考虑到空间平台的供电因素,载荷激光雷达无法长时间连续工作,点云模型较稀疏。本文的融合方法对上述两种点云进行融合,融合初值较准确,迭代次数少,效率较高;比较发现,融合点云密度有很大的提升,误差小于可见光图像三维重建点云,与激光雷达点云误差相近,且融合后点云的缺损部分也得到了补充,保留了目标的纹理特性,点云完整性得到很大的提升。
