基于EMD-WDD-MK模型的玛纳斯河年径流预测
2021-11-29闫国辉乔长录陈伏龙
闫国辉,乔长录,陈伏龙
(石河子大学水利建筑工程学院,新疆石河子832000)
0 引 言
径流预测是进行流域水资源优化配置的前提,但是目前还难以用物理成因分析法准确预报未来某一时段的径流值。径流过程是一个十分复杂的过程,涉及水文与气象等多个因素,受随机因素的影响,过程表现出非线性且非平稳的特点[1]。径流预报的主要方法有传统统计方法、概率论方法、模糊集理论等方法[2-4]。随着计算机技术的进步,新的预测方法也逐渐出现,例如支持向量机、人工神经网络以及模糊数学等。同时对径流内部变化规律的掌握,以及对径流序列中噪声的处理,也有助于提高模型预测精度。目前常用的径流序列分析方法有主成分分析法、小波分解方法、经验模态分解法(Empirical Mode Decomposition,EMD)和变分模态分解法(Variational Modal Decomposition,VMD)[5-7]。新方法的产生,并不代表着旧方法的落伍。寻求不同方法的优点,并将不同方法进行耦合建模,构建具有更高预测精度的预测模型是目前径流预测的一个新的研究方向。陈旭等[8]提出了基于EMD 和PSO 的耦合模型,对汾河上游的年径流进行了预测,得到了较为满意的结果。吕晗芳等[9]构建了VMD-LSSVM 模型,对上静游等水文站的月径流进行了预测,并与单一LSSVM 模型预测结果进行对比,提高了模型的预测性能。梁浩等[10]构建了多种模型耦合的预测模型,对渭河流域的径流进行了预测,体现了"分解-合成"预测方法的适用性。但目前对EMD方法应用时,多数未考虑到分解得到的高频分量中含噪声信号过多,未对高频分量进行处理。且目前基于EMD 与VMD 构建的耦合模型,多用于内陆河流,在西北干旱区河流的适用性和可行性需要进一步验证。
在水资源配置与规划越来越严格的今天,对规划年河流来水量的预测变得更加重要,在缺水的西北干旱区这种情况尤为明显。由于径流预测研究中以西北干旱区内陆河为对象的研究较少,且西北地区较为缺水,需要对规划年的径流量有更高精度的预测。为了提高干旱区河流年径流预测精度,使农业及城市配水有更可靠的依据,本文将EMD 与VMD 分别与加权马尔可夫链进行耦合建模,并引入小波降噪,构建EMD-MK、EMD-WDD-MK 和VMD-MK 模型。以位于西北干旱区的玛纳斯河(以下简称玛河)为例,进行该方法的应用研究,以期建立一种适合干旱区河流的年径流预测模型,为玛河流域水资源配置与规划提供可供参考的依据。
玛河位于新疆准噶尔盆地南部,干流全长324 km,流域面积33 500 km2,地处干旱区内陆,属于典型的温带大陆性气候,平均气温为4.7~5.7 ℃。该河发源于天山北坡,是天山北麓径流量最大的河流,主要以冰川融水及降雨为补给,冰雪融水补给占46%,降雨占26%,降雪18%,最后流入尾闾玛纳斯湖[11,12]。
1 模型构建
1.1 经验模态分解法(EMD)
Huang 等[13]于1998年提出了经验模态分解法,该方法对处理非线性或非平稳时间序列方面具有较强自适应性。本质上,EMD 可以对非平稳时间序列进行处理,并逐渐将序列分解为不同频率的曲线和趋势,从而获得不同特征尺度序列的一种方法。每个序列称为本征模式函数(Intrinsic Mode Function,IMF),原始序列的趋势或剩余量通常是最低频率的IMF 分量。本征模态函数必须满足2 个条件:①相对于时间轴来说数据表现出局部对称性,即在任何时间点局部平均值都为零[14];②数据系列中,极点和零点在数量上必须相等或者最多相差1 个。经验模式分解的结果可表示为[15]:
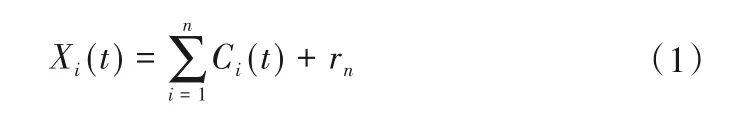
式中:Ci(t)为对应原始序列中不同特征尺度的序列分量;rn为剩余分量,可以表现原始序列X(t)的趋势变化。
1.2 变分模态分解法(VMD)
Dragomiretskiy 等[16]于2014年提出了一种处理非平稳时间序列的新方法,即变分模态分解法(VMD)。VMD在分解序列过程中,采用非递归和变分分解对序列进行处理,将序列分解成几个分量和一个趋势向量。
VMD将变分问题引入到时间序列的处理中,其关键内容是变分问题构建完之后,对问题的求解。在将原始径流序列输入算法中后,经过算法运算,将输出K个模态函数uk(t),其目的是为了将模态的估计宽带之和最小。分解中变分约束模型如下式所示[17]:
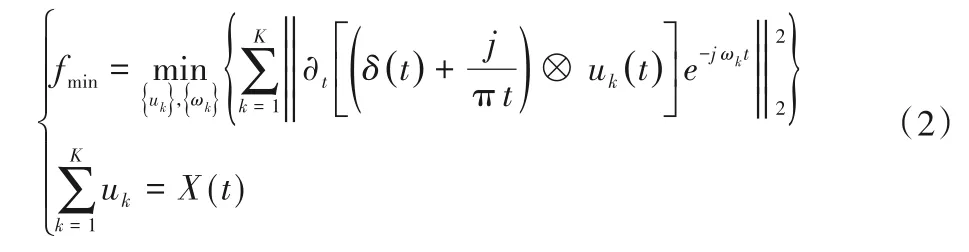
式 中:{uk}={u1,u2,…,uK}是模态函数的集合;{ωk}={ω1,ω2,…,ωK}是对应模态函数中心频率的集合;δ(t)为狄克拉函数;⊗为内卷运算符。
1.3 马尔可夫链预测的方法
马尔可夫过程是一类随机过程,其最基本的特征是“马氏性”,也称“无后效性”,即在系统(随机过程)的“现在状态”已知的条件下,其“将来状态”与“过去状态”无关。马尔可夫链定义如下:
考虑随机过程{xn,n∈T},若对任意整数n∈T和任意i0,i1,…,in∈T,条件概率满足:
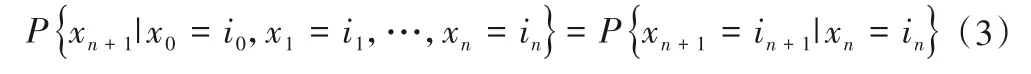
也就是说此时状态的概率只与前一个时刻所处的状态相关,与其他时刻所处的状态无关,那么过程{xn,n∈T}为马尔可夫链[18]。
一般考虑齐次马尔可夫链,即对任意的m,k∈T有:
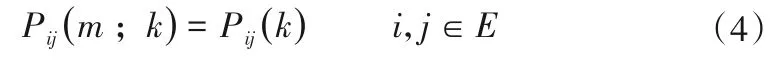
式中:Pij(m;k)为系统在m时刻处在状态i,经过k步转移至状态j的概率;Pij(k)为系统从状态i,经k步转移至状态j的概率,此时转移概率与初始时刻无关,k取1时,Pij(1)记为Pij。
1962年,Thomas和Fiering[19]第一次利用一阶马尔可夫链来模拟河川径流,之后更多的学者将马尔可夫链用于径流预测中。McMillan 等[20]通过马尔可夫链-蒙特卡罗采样方式,建立了径流预测模型。随着科学技术的进步,以及计算机的产生与发展,马尔可夫链开始与智能算法相结合进行径流预测。Aksoy 等[21]基于马尔可夫链和合成数据提出条件人工神经网络模型对某干旱区月降水量进行了预测。国内也有很多学者进行马尔可夫链预测径流的研究工作,例如,韩贻强[22]基于传统马尔可夫链对大沽夹河年径流状态进行预测。沈冰等[23]基于改进的加权马尔可夫链径流预测模型对宝鸡市的渭河年径流量进行预测。蓝永超等[24]结合时间序列分析和马尔可夫链建立了时间序列-马尔可夫链耦合模型,并对黄河上游的年径流进行多年的预测。刘新有等[25]以状态预测概率为权重,将传统马尔可夫链径流预测模型得出的预测状态加权求和,实现了径流数值预测并对怒江干流进行了预测。对于时间离散且状态离散的时间序列,随机过程预测方法的运用变得越加广泛,马尔可夫链预测就是其中最重要的一种[26]。
1.4 EMD-WDD-MK 模型构建
EMD-WDD-MK 模型的预测方法步骤:①首先利用EMD 方法将年径流序列进行分解,可分解得到几个IMF 分量和一个剩余分量;②由于EMD 分解得到的IMF1-IMF3 分量为高频含噪声分量,所以使用小波阈值法进行降噪处理;③使用马尔可夫链对高频降噪后的IMF 分量以及低频IMF 分量进行预测,预测中引入级别特征值,定义级别特征值H为:
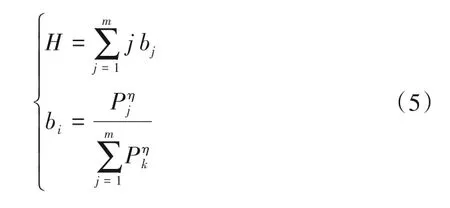
式中:η为概率作用系数,取值通常为2 或4,取值越大,大概率的影响就会越大。依据概率最大隶属度原则判断分量的分级状态后,由式(6)计算分量的预测值[25]:
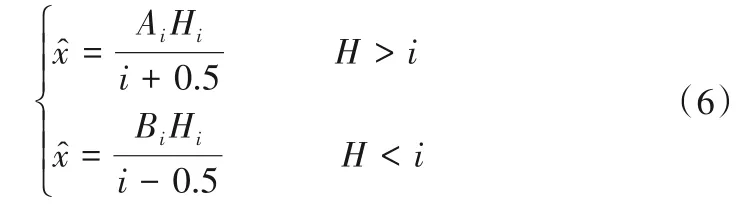
式中:̂为年径流量的预测值;Ai、Bi分别为状态i区间的上限值和下限值。
④将IMF 分量及剩余分量的预测结果进行重构,重构所得的量即为该预测模型的年径流量预测值,然后进行误差分析与计算。
1.5 模型评价指标
为了对比EMD-MK、EMD-WDD-MK 和EMD-VMD 三种模型的预测结果精度,本文选取了预报合格率(QR)、平均绝对误差(MAE)、平均相对误差(MAPE)和均方根误差(RMSE)4 种指标判定模型的预测性能。计算公式如下:
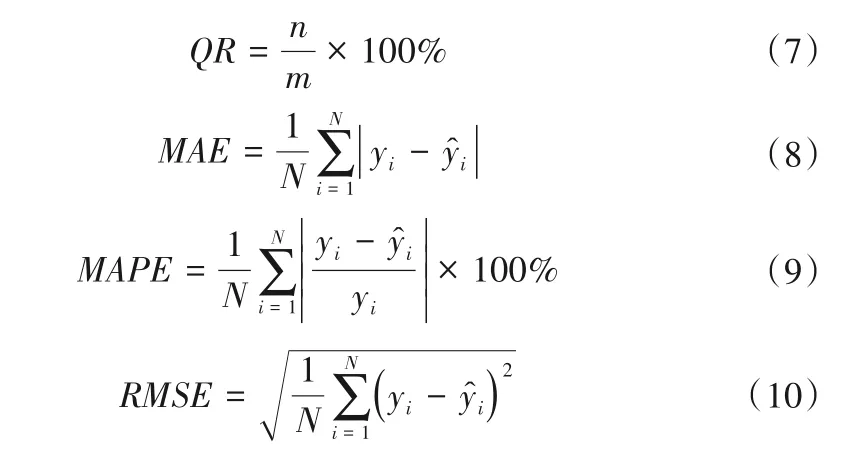
式中:n为预测结果合格的个数;m为总预测结果个数;yi为实测年径流量模型预测得出的年径流量。
2 玛河年径流预测
2.1年径流序列的分解
利用EMD 与VMD 对玛河肯斯瓦特水文站1956-2012年的年径流序列进行分解,分解结果如图1 和图2 所示。模型以两种分解方式分解得到的1955-2012年分量为模型的率定期,以2013和2014年为模型预测结果的验证期,通过对比3种模型在验证期的预测结果精度,来判断模型的预测水平。
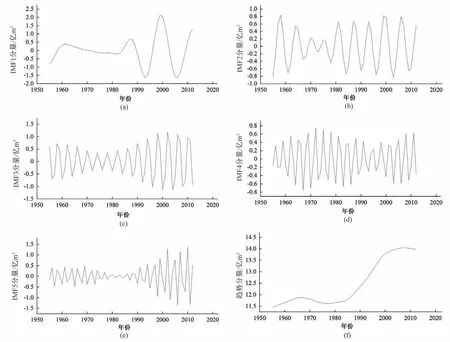
图2 玛河1955-2012年年径流量序列VMD分解Fig.2 VMD decomposition of annual runoff series of Mahe River from 1955 to 2012
由图1 可知,年径流量时间序列的IMF 分量表现了该时间序列在频率、振幅和波长方面的变化。其中IMF1 分量具有频率最高、振幅最大、波长最短的特点,且由IMF1 分量到IMF5 分量,分量的振幅逐渐减小、频率逐渐降低、波长逐渐变长。同时,玛河年径流量的IMF1-IMF5 分量分别具有准3~6 a、准6~9 a、准8~10 a、准11~15 a 和准35 a 的波动周期。根据分解所得的趋势分量可以看出玛河1955-2008年的年径流量一直处于上升趋势,2008年以后,上升趋势逐渐平缓。
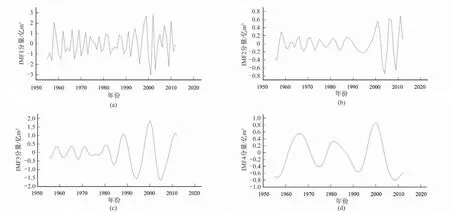

图1 玛河1955-2012年年径流量序列EMD分解Fig.1 EMD decomposition of annual runoff series of Mahe River from 1955 to 2012
与EMD 分解所得向量不同,图2 中VMD 分解所得分量表现由IMF1 分量到IMF5 分量的振幅逐渐变大、频率逐渐增高和波长逐渐缩短的特点。通过与EMD分解得到的趋势向量相比,VMD 分解得到的趋势分量在反映径流变化过程中更为精确。图2中趋势分量在2008年以后的趋势情况与图1中的趋势分量大致相同,都表现为上升趋势逐渐平缓并有下降趋势。
2.2 小波阈值降噪
由于人为因素以及自然因素的影响,采集整编得到的径流资料往往含有随机噪声,这会造成径流序列的信噪比降低,所以需要采用一些方法对原始径流资料消去噪声处理,提高资料序列信噪比,进而提高预测精度。
在EMD分解得到的年径流序列的各分量中,高频分量中所含的噪声较多,所以选择IMF1-IMF3分量进行小波阈值降噪处理。处理过程中,通过对比不同处理方法所得去噪序列的信噪比(SNR)和均方根误差(RMSE)。在硬阈值、软阈值和固定阈值降噪处理3 种处理方法中,选取SNR较高,RMSE较低的方法进行降噪处理。对IMF1~IMF3 分量的降噪处理结果如图3所示。
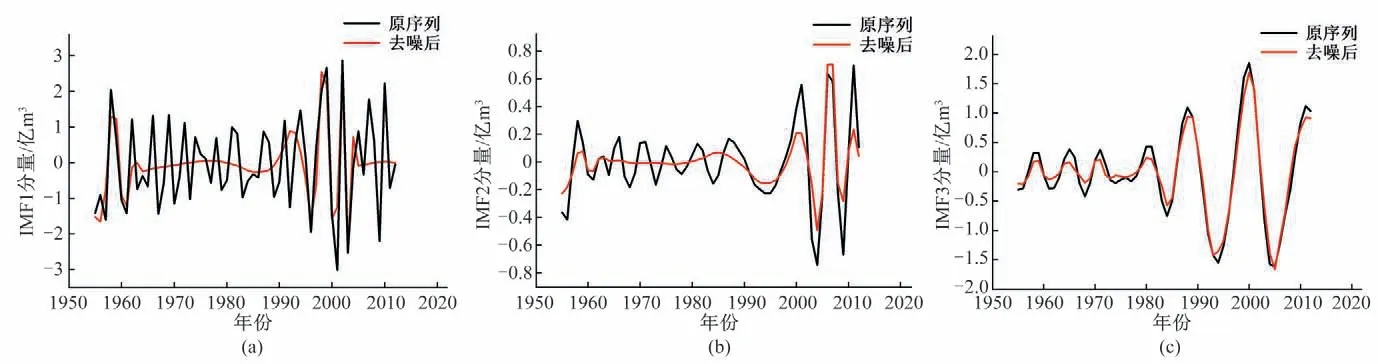
图3 IMF1-IMF3分量降噪结果图Fig.3 Denoising results of IMF1-IMF3 components
2.3 马尔可夫链预测
2.3.1 计算均值与标准差
以EMD 分解得到,并通过降噪后的IMF1 分量的预测为例进行预测求解。根据IMF1 分量的数据,用式(11)和(12)分别计算出径流序列的均值和均方差,计算结果序列均值为xˉ=-6×106m3、序列标准差为S=8.8×107m3。
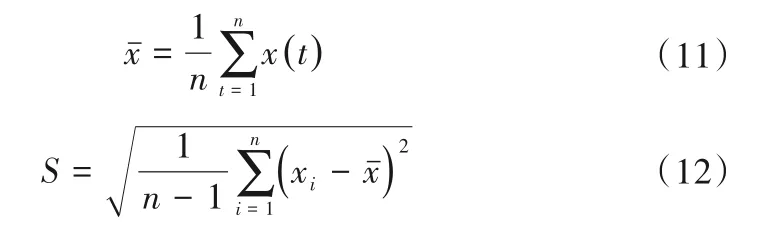
2.3.2 IMF1分量分级
如表1 所示,根据计算得到的均值和均方差,把IMF1 分量序列划分低、偏低、平、偏平、高等5个状态。

表1 状态分级表Tab.1 Status classification table
通过状态分级表,将IMF1 分量序列中的数据进行状态划分,结果如表2所示。
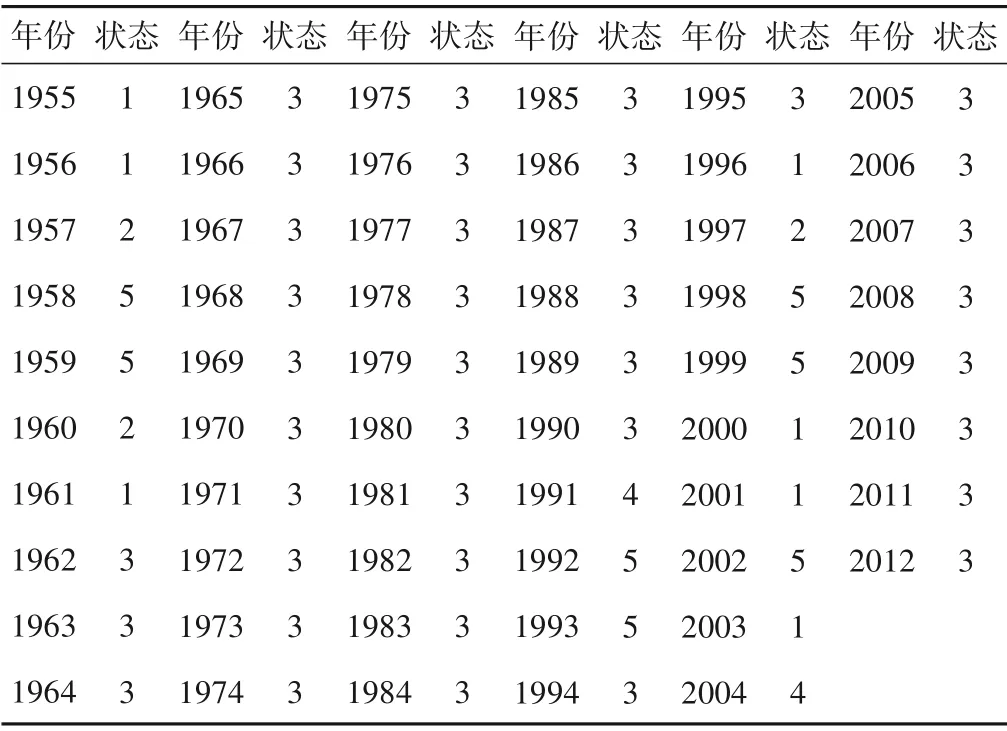
表2 IMF1分量序列及状态Tab.2 IMF1 component sequence and status
2.3.3 建立状态转移概率矩阵
根据IMF1 分量序列中各年的状态,可以得到不同步长的马尔可夫链转移概率矩阵。经整理计算,各步长状态转移概率矩阵如下:

2.3.4 计算自相关系数
利用式(13)、式(14)分别计算得IMF1 分量序列的各阶自相关系数和归一化权重,并将各阶自相关系数归一化后作为各步长的马尔可夫链权重,结果如表3所示。
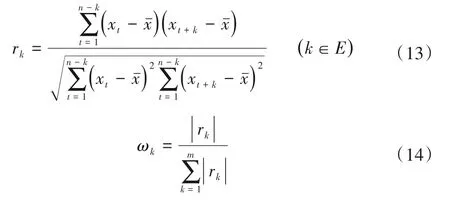

表3 各阶自相关系数及归一化Tab.3 Autocorrelation coefficients and normalization
2.3.5 状态预测
根据IMF1分量1955-2012年状态转移矩阵对2013年IMF1分量状态进行预测,结果见表4。
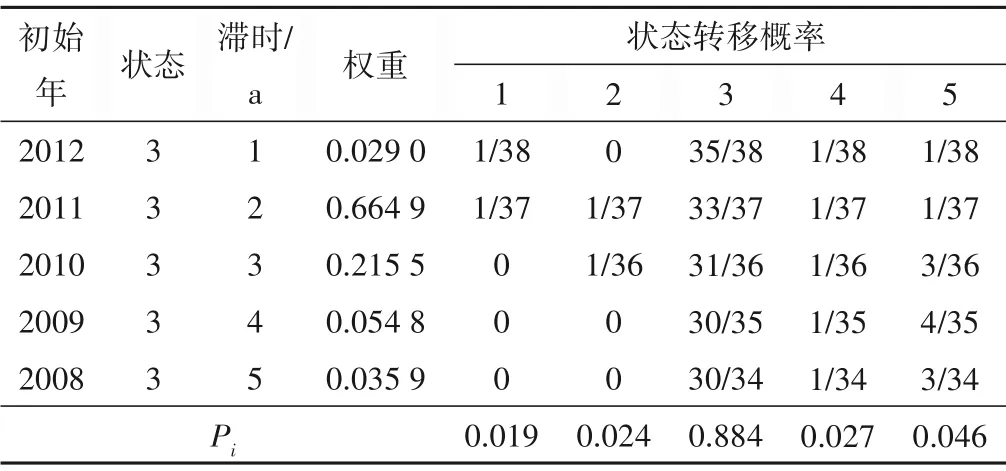
表4 IMF1分量状态预测Tab.4 IMF1 component state prediction
由表4可得max{Pi,i∈E}= 0.884,该权重和所对应的i= 3,根据最大隶属度原则,可以预测IMF1分量2013年值的状态为状态3。之后将IMF1分量2013年的预测值加入IMF1序列中,以1955-2013年的序列资料预测2014年的IMF1 分量状态,状态预测的结果见表5。
由表5可知max{Pi,i∈E}= 0.887,该权重和所对应的i= 3,根据最大隶属度原则,可以预测2014年IMF1 分量为状态3。
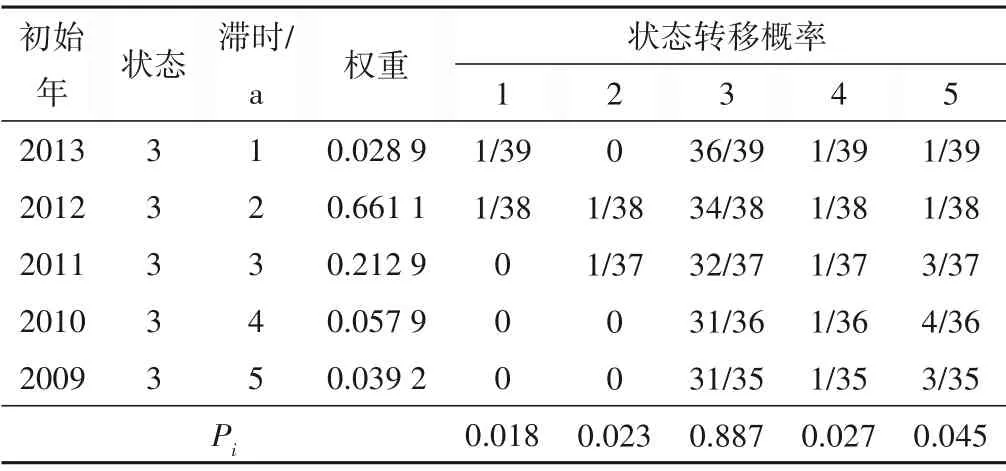
表5 IMF1分量2014年状态预测Tab.5 Status prediction of IMF1 component in 2014
2.3.6 预测值计算
根据模糊集理论中的级别特征值,根据式(5)和式(6)分别求出级别特征值和该年的预测值。为了突出较大概率隶属度的作用,本文中η取2,把表3和表4中的数据分别代入(5)和式(6)中,分别计算出H 和x̂。经过计算2013年与2014年EMD 分解得到的IMF1分量的预测值别分别0.33和0.33,对每个分量进行重复计算,即可得出各分量的预测值,通过重组可得预测年份的年径流量。
2.4 预测结果对比分析
对3 种模型中不同分量进行加权马尔可夫链预测并重构,得出2013 和2014年3 种模型不同的预测值,计算结果如图4所示。
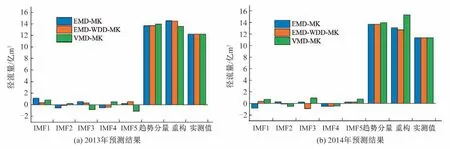
图4 玛河2013和2014年年径流量预测结果Fig.4 Annual runoff forecast results of Mahe River in 2013 and 2014
由图4 可知,EMD-MK 模型所得2013年和2014年玛河年径流量预测结果分别为14.53 亿m3和13.08 亿m3,相对误差分别为18.81%和15.04%。VMD-MK 模型的预测结果分别为13.58 亿m3和15.33 亿m3,相对误差分别为11.04%和34.83%。EMD-WDD-MK 模型在2013年和2014年的年径流量预测值与实测值的相对误差分别为18.32%和11.87%。
结合图4 与表6 可以看出,虽然VMD-MK 模型在2013年的预测结果相对误差相较于其他模型较小,但是2014年的预测结果误差达到了34.83%,使其合格率低于70%,超出了可以参考的误差范围。在合格率方面,EMD-MK 模型与EMD-WDD-MK模型在2013年和2014年的预测值与实测值相对误差均小于30%,预测结果都为合格。在平均绝对误差的对比中可以发现,引入小波降噪的EMD-WDD-MK 模型比EMD-MK 模型的平均绝对误差减小了0.21。在平均相对误差和均方根误差的对比中,也体现出EMD-MK 模型优于VMD-MK 的耦合模型,且EMD-WDD-MK 模型的表现最优,其精度也是3 种模型中最高的。
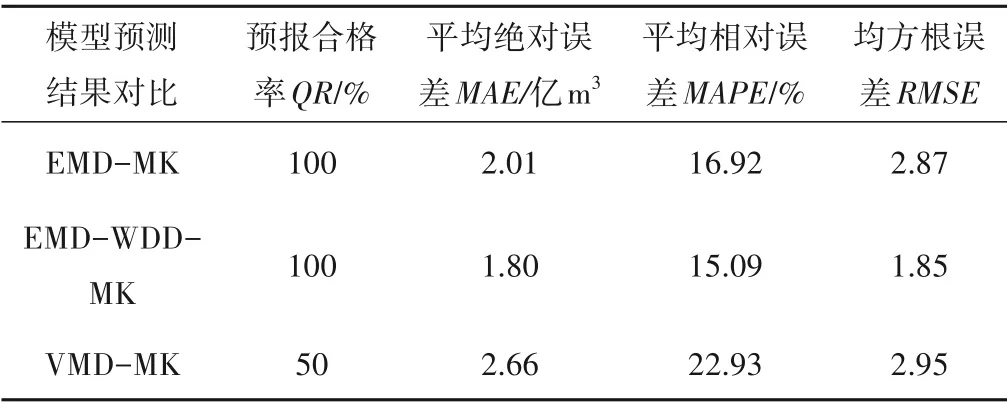
表6 玛河各模型年径流预测结果Tab.6 Annual runoff prediction results of each model of Mahe River
3 结 论
(1)利用本文构建的EMD-MK、EMD-WDD-MK 和VMDMK 模型对玛河2013年和2014年的年径流量进行了预测。通过对比预测结果的误差,可以得出EMD-WDD-MK 模型相较于其他模型预测更为准确的结论。
(2)利用EMD 与VMD 分解方法对年径流量序列进行分解有助于了解径流周期变化的特征,并且能将非线性、非平稳年径流序列转化为平稳时间序列,有助于提高预测的准确性。同时使用小波阈值法,对高频含噪声的IMF1-IMF3分量进行降噪处理,降低噪声对预测结果的影响,进而提高预测精度。
(3)与普通的马尔可夫预测相比,加权马尔可夫链以归一化各步长的自相关系数为权重,更能充分发挥资料系列自身的相关性,且具有更好的精度。同时文中使用均方差将资料序列进行分级,更能体现资料序列的自身特点,分区更合理。
(4)随着实测数据的增加,时间序列不断延长。自相关系数、状态转移矩阵和权重有更多资料的支撑,会发生某些变化,这种变化使得预测模型不断完善,预测精度也在不断地提高。所以在序列中加入新的实测数据是十分重要的,这样可以为径流预测的结果提供更多的资料支持。 □
