应用均值漂移的印花面料交互式换色方法

胡 群， 张 宁， 潘如如

(生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

印花面料设计师借助计算机辅助系统(CAD)设计花型，生产人员根据花型颜色分开制版进行打样。花型设计专业度要求高,分色制版耗时费力，花型颜色变换、生产系列产品困难。通过获取印花图像分色来实现面料分色换色的方法，可模拟印花面料打样效果，快速生成系列产品，为设计人员提供参考，节约时间成本。

当前主要的图像换色方法可分为颜色迁移法[1]和直接换色法[2]两大类。二者最本质的区别在于参考图像的有无，本文侧重于使用直接换色法对已有织物的颜色进行调节。基于颜色迁移的换色是通过信息匹配的方法，将参考图像的颜色转移到目标图像上。Reinhard等[1]提出了一种在lαβ颜色空间下，基于亮度匹配的颜色迁移算法。Han等[3]在前人研究的基础上提出了一种基于参考颜色的颜色迁移方法，对色织物进行实验可获得自然的换色结果。以上方法没有对参考图像的选择提出优化方案，难以规避由于目标图像和参考图像之间存在匹配度差异而产生的不良结果。直接换色法规避了参考图像的选择问题,通过对目标图像进行区域分割的方法，提取图像主色，调整待换色区域的颜色并建立映射关系来实现图像换色。其中主要包括交互式的方法和深度学习的方法，基于交互式的方法主要通过图像分割的方法提取调色板，通过调节调色板来实现换色，如结合图像分割与区域生长法的图像换色[4]，调色板自动提取的换色[5-6]，考虑显著颜色的换色[7]。直接对图像分割的方法难以适应颜色丰富、纹理显著的面料换色，面料图像的纹理会对分割结果造成影响。基于深度学习的方法，如Li等[8]结合卷积神经网络对灰度图像进行自动着色，着色效果自然逼真。机器学习与深度学习的方法依赖大规模的样本数据，面料样本难以收集，上述方法仍需要进行改进。

基于此，本文提出一种基于纹理平滑与图像分割的交互式印花面料分色换色方法。采用相对总变差模型对面料图像进行平滑处理，去除面料的纹理信息，再转换到颜色均匀的CIE1976L*a*b*色彩空间，便于后续分割。采用Mean-shift聚类算法对图像进行分割并提取面料的分色，建立颜色映射关系，将调节后的颜色映射到原图像上，实现面料的分色换色。

1 图像采集与预处理

1.1 图像采集

面料的颜色信息容易受到多种因素的干扰，采用标准的采集环境能够避免对后续的分割和换色产生影响。DigiEye是用于测量颜色和捕获高质量可重复图像的计算机数码相机系统,采用该系统对收集的印花面料进行图像采集。系统配置尼康D7000相机和D65标准光源，分辨率为96 dpi。

1.2 图像平滑

织物图像是一种典型的结构纹理图像，织物的纹理会影响后续的图像分割以及换色结果，故需对采集得到的图像进行平滑。采用相对总变差模型[9]对采集得到的面料图像进行平滑处理，目标函数为

(1)

式中：i,j表示像素点在图像中的位置；S(i,j)表示输入图像；T(i,j)表示结构提取图；argmin表示使其后式达到最小值时点(i,j)的集合；(T(i,j)-S(i,j))2确保了输入和输出的差异最小。式(1)后半部分基于相对总变差模型对图像矩阵进行了正则化处理，是从图像中移除纹理的关键。其中：λ为可控参数;ε为一个趋向无穷小的正数，用来确保分母不为零;Dx(i,j),Dy(i,j)为总变差，具体表达式如下：

(2)

式中：k,l表示窗口中图像像素点的位置；∂x和∂y为2个方向的偏导数；g为根据空间关联性定义的加权函数，可表示为

(3)

式中，σ为调节窗口空间尺度的参数。为从纹理信息中区分出突出的结构，定义了窗口内变差Lx(i,j),Ly(i,j)：

(4)

可通过调节参数λ与σ来控制图像的平滑程度，其中参数λ控制图像的光滑程度，参数σ控制式(3)窗口的大小。通过平滑实验发现，λ取值为0.006，σ取值为4时，平滑效果最优。采用上述参数对图1(a)中采集并剪裁后的印花面料图像进行纹理平滑，得到如图1(b)所示的去纹理面料图像。

图1 印花面料及平滑图像示例Fig.1 Examples of printed fabric image (a) and smoothed image(b)

1.3 颜色空间转换

CIE1976L*a*b*(以下简称L*a*b*)颜色空间与人类视觉对颜色的感知十分接近，是一种均匀的颜色空间，不依赖采样设备与环境，在图像分割领域表现效果优异。图像从RGB转换到L*a*b*颜色空间需先转换到XYZ颜色空间，转换公式如下：

(5)

式中，R、G、B与X、Y、Z分别表示RGB与XYZ颜色空间对应的三通道颜色数值。XYZ颜色空间转换到L*a*b*颜色空间的转换公式如下：

(6)

(7)

式中：Xn、Yn、Zn默认取值为95.047、100.0、108.883；L*、a*、b*表示L*a*b*颜色空间三通道的值。文献[10]描述了RGB颜色空间与L*a*b*颜色空间之间的相互转换。本文将经平滑处理后的图像转换到L*a*b*颜色空间进行聚类分割与分色换色操作，将结果从L*a*b*颜色空间转换到RGB颜色空间输出。

2 图像分割与换色方法

2.1 图像分割

图像分割是指将图像分成若干互不重叠的子区域，使得同一个子区域内的特征具有一定的相似性、不同子区域间的特征有明显的差异性。本文采用聚类的方法来实现面料的图像分割。Mean-shift聚类算法是一种基于密度的统计迭代算法，该算法仅依靠样本空间点进行分析，收敛速度快，被广泛应用于计算机视觉领域[11]。算法迭代步骤如下：1)以带宽h做一个漂移窗口，计算中心点x0移动到窗口内周围点xi所需要的偏移量之和，求取平均值得到平均偏移量M(x0)；2)点x0向平均偏移量方向漂移得到新的中心点x0′；3)重复上述步骤直至算法收敛。偏移均值M(x0)可表示为

(8)

式中：sh表示以x0为中心点，半径为h的高维球区域；k为在sh范围内点的个数；xi是在sh范围内的点。通过式(9)可得到新的中心点：

x0′=M(x0)+x0

(9)

引入核函数的偏移均值m(x0)，可以将低维的不可分数据变成高维可分数据，具体公式如下：

(10)

式中，函数g表示对核函数的导数求负。

上述算法中，带宽h是影响算法迭代结果的重要参数。通过实验优选发现，当h为0.11时，分割效果最好。采用上述分割算法及优选的带宽h对平滑后的L*a*b*颜色空间下的面料图像进行分割，得到如图2所示的印花面料分色结果。

图2 印花面料分色图Fig.2 Separated image of printed fabric

2.2 图像换色

图像换色旨在通过更改图像中的某一类或某几类颜色来更改图像的配色方案。在通过聚类分割的方法获取图像的分色后，选择面料分色，通过交互的方式调节颜色滑块，对该聚类中心的颜色值进行调整得到新的颜色。建立调整后的颜色与原来颜色的映射关系,将调整后的颜色映射到对应的分割区域，从而得到分色换色结果。

假设大小为M×N的织物图像为IM×N×3，其中3为图像的通道数，通过式(11)转换函数将图像转换成大小为(M×N,3)的二维矩阵：

I(M×N,3)=f(IM×N×3)

(11)

式中：f为转换函数；I(M×N,3)为一个3列的矩阵。其中L*、a*、b*三通道数值各为1列。分色换色公式为

(12)

图3 印花面料分色换色Fig.3 Separated color replacement of printed fabric

3 结果与分析

本文采用MatLab编写图形用户界面(Graphical User Interface)，实验在Intel 2.20 GHz处理器和12 GB RAM的笔记本电脑上进行。

3.1 平滑对比

为证明平滑算法的有效性，对同一印花面料在带宽h取值相同的情况下，进行了平滑分色换色以及无平滑分色换色的对比实验，实验结果如图4所示。由于纹理信息的影响，直接对图像进行分割，会出现许多分散性的细小毛刺，导致后续换色出现换色疵点。而经过平滑处理后的图像分割结果细致、完整且无分散毛刺，无换色疵点出现。对比换色结果可知，增加平滑算法后，分割结果更为完整，换色结果更为自然真实。

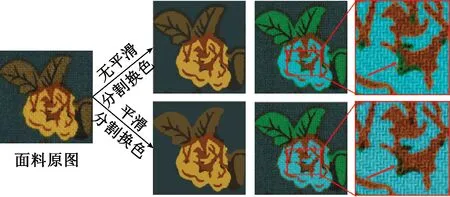
图4 分色换色对比图Fig.4 Separated color replacement comparison

3.2 参数优选

3.2.1 平滑参数

基于相对总变差模型的图像平滑算法中，可调参数λ与σ直接决定平滑结果，其中λ的取值范围为0.001～0.03，σ的取值范围为0～8。由于不同种类、不同材料的面料其纹理显著性存在着明显的区别，本文选取了不同的印花面料进行平滑参数调节实验。图5示出控制平滑程度的参数λ的调节情况。可以看出，随着λ值的增大，平滑后的面料图像模糊程度加深。当λ取值为0.01时，3种面料图像均出现不同程度的模糊；而当取值较小，如当λ取值为0.002时，平滑处理后的图像又会出现纹理去除不完全的现象。结合本文实验，λ取值为0.006时可以获得清晰的去纹理平滑图像。

图5 平滑参数λ调节Fig.5 Smoothing parameter λ adjustment

参数σ决定了平滑算法的窗口空间尺度，随着σ取值的增大，对图像纹理的抑制效果也更好。如图6所示，当σ取值大于4时，算法逐渐收敛。对平滑参数进行调试实验发现，参数σ取值为4时可得到纹理去除完全的平滑图像。

图6 平滑参数σ调节Fig.6 Smoothing parameter σ adjustment

3.2.2 带宽参数

Mean-shift算法中，带宽h决定了漂移窗口的大小，影响面料分割的细致程度。当h取值较小时，聚类数目较多，面料分割细致，细节保留完整，但迭代时间增加；当h取值较大时，聚类数目减少，面料分割趋向轮廓化，细节残缺，迭代时间减少。图7示出带宽h的调节实例，综合上述因素，实验设定带宽h为0.11，可取得分割细致清晰的结果。

图7 带宽参数h调节Fig.7 Bandwidth parameter h adjustment

3.3 结果分析

为证明本文方法的有效性和可行性，基于优选的模型参数，选取不同的印花面料进行单分色换色以及多分色换色的实验，结果如图8所示。其中图8(a)示出仅对印花面料的一个分色进行调节的换色实验结果；图8(b)示出对面料的多个分色进行调节的换色实验结果，换色结果真实。在面料设计前期可为面料花型设计者提供试色参考，也可辅助设计者快速得到系列图像。本文的方法具有很好的鲁棒性，对花型复杂、颜色变化多的印花面料进行单色换色以及多色换色实验，均能得到细节纹理保留完整，颜色外观自然真实的结果，可为面料设计工作者提供便利。

图8 换色实验结果Fig.8 Color replacement test results. (a)Single separated color replacement; (b) Multiple separated colors replacement

3.4 方法对比

为了证明Mean-shift算法的优越性，实验比较了颜色量化算法[12]、K均值(K-means)聚类算法[13]和Mean-shift算法的分割效果。在其他条件相同的情况下，对相同的面料图像进行分割，分割效果对比见图9。

图9 分割算法比较Fig.9 Segmentation algorithm comparison

颜色量化算法将图像转换到HSV颜色空间进行量化统计，用量化后颜色集的平均值作为聚类中心，实现图像分割。该方法依赖于量化的区间划分，容易出现不同种类的颜色合并，从而导致聚类后的颜色与原始图像存在较大差异，并不适用于面料图像的分割。K-means聚类算法快速简单，但需人为辨别聚类的簇数，分割一些同类色繁多且细节明显的面料时，难以分割边缘细节部分。对比之下，Mean-shift算法能够适应不同种类的面料图像，分割效果优于其他分割算法，尤其是边缘细节部分的分割效果具有可区分性。

4 结 论

本文提出了一种基于纹理平滑和Mean-shift图像分割的印花面料分色换色方法，采用相对总变差模型去除面料的纹理，利用Mean-shift聚类算法提取图像分色，建立待换颜色与目标颜色之间的映射关系，实现分色换色。采用不同的印花面料图像进行实验，可得到结构纹理清晰且自然的系列换色结果，验证了本文方法的可行性和有效性。通过对不同的分割算法进行比较，验证了方法的优越性。对于颜色繁多的面料，分割得到的颜色数量多，增加了调色的困难度，如何进一步优化算法解决同类色的合并问题是未来研究需要解决的问题。

FZXB