复杂磁化下硅钢片矢量磁致伸缩特性测量与模拟*
2021-11-29樊小鹏周永言张艳丽张殿海
李 丽, 樊小鹏, 周永言, 张艳丽, 张殿海
(1. 广东电网有限责任公司 电力科学研究院, 广州 510082; 2. 沈阳工业大学 电气工程学院, 沈阳 110870)
随着人们环保意识日益增强,电机、变压器等电工设备的振动、噪声污染等逐渐成为公众关心的热点问题[1].电工设备产生的振动噪声从来源可分为气动噪声、机械噪声和电磁噪声,其中电磁噪声主要源自于绕组与周围漏磁场相互作用产生的洛伦兹力和铁心硅钢片在交变磁场作用下的磁致伸缩力[2-4].磁致伸缩是指铁磁材料在被周期变化磁场磁化时,外形尺寸表现出微小的周期性的伸长或收缩现象[5].大型电工设备铁心尺寸很大,因此磁致伸缩效应产生的振动噪声占比也较大.研究铁心硅钢片磁致伸缩特性的测量和建模方法对设计制造低振动噪声电工设备具有重要意义.
目前,针对硅钢片磁致伸缩特性的测量主要基于应变计测量法和激光测振测量法,这两种方法在国际上都有使用,且各有优缺点.Gong等[6]采用激光测振法测量并分析不同交变磁化下硅钢片磁致伸缩特性,激光测振法比应变计法精度要高,但是所需要的测量系统也更加昂贵和复杂.Zhang等[7]则采用三轴应变片对硅钢片交变磁场磁化下的磁致伸缩特性进行了实验测量研究.由于此方法可以同时采集三个不同方向上的磁致伸缩随磁通密度的变化,根据材料力学相关原理可以得到主应变的大小和方向,从而得到磁致伸缩特性为各向异性的结论.2014年,日本学者Enokizono教授团队同样利用三轴应变片法测量并分析了取向硅钢片的矢量磁致伸缩特性[8];张艳丽教授团队利用一套综合磁特性测量设备,采用三轴应变计作为应变检测传感器,分别测量了硅钢片交变磁化、旋转磁化以及直流偏磁下的磁致伸缩特性[9-11].测量结果表明,取向和无取向硅钢片的磁致伸缩均表现出各向异性特性,与磁特性相类似,磁致伸缩特性具有矢量和滞后双重特性.
为计及硅钢片磁滞和频率对磁致伸缩特性的影响,Zhu等[12]提出了基于神经网络的磁致伸缩模型,实验结果表明,磁致伸缩的滞后特性对计算结果有很大影响,在计算中应予考虑.Wakabayashi等[13]在描述矢量磁特性的Enokizono & Soda模型基础上,提出了描述矢量磁致伸缩特性E&S-W数学模型;李强[14]和周航[15]分别利用交变和旋转磁化下磁致伸缩的测量数据建立了相应的动态矢量模型.综上,国内外学者在不同磁化情况下磁致伸缩特性模拟方面取得了丰富的研究成果,但是考虑非正弦磁化下的硅钢片磁致伸缩模型的研究尚未开展.
本文针对单片无取向硅钢片在非正弦磁场磁化下的矢量磁致伸缩特性展开测量和模拟方法的研究.基于现有磁致伸缩特性测量系统,测量并分析几种典型高次谐波磁场对磁致伸缩特性的影响.从频域角度推导出表征非正弦磁场磁化下的磁致伸缩特性动态矢量数学模型,同时给出相应的模型参数数据库的建立方法,并验证了模型的有效性.
1 硅钢片矢量磁致伸缩特性测量
1.1 测量方法
为了得到硅钢片矢量磁致伸缩特性,本文采用基于三轴应变花传感器的磁致伸缩测量系统来获取不同方向的磁致伸缩特性,整体测量系统组成如图1所示.为简化实验测试平台的搭建,同时考虑到测量结果的一致性,测量系统中的励磁部分沿用实验室现有的德国Brockhaus硅钢片单片磁特性测量系统,系统主机可以控制激励形式,实现在被测样片中产生叠加不同谐波的交变磁场.励磁绕组形成一个空间有限的内腔,测量时将待测样片置于内腔内.本文采用的测量样片牌号为B50A600无取向硅钢片.

图1 矢量磁致伸缩特性测量系统框图Fig.1 Block diagram of measurement system of vector magnetostriction characteristics
由于硅钢片磁致伸缩主应变的方向和磁化方向不一致,单纯检测磁化方向的磁致伸缩形变并不能准确获取样品内主应变的特性.因此采用三轴应变花拾取样片的应变信号.考虑到测量区域面积和测量参数,应变花采用日本共和公司生产的产品,其型号为KFG-10-120-D17-11.为后面数据处理方便起见,固定应变花时,应保证其长度方向与硅钢片的轧制方向一致.这样,通过三通道动态应变仪就能同时检测硅钢片沿轧制、垂直于轧制和45°三个方向的磁致伸缩形变信号,通过材料力学的相关原理,可以得到磁致伸缩伸长主应变或收缩主应变以及对应的主应变.
1.2 测量条件与结果
由于硅钢片磁特性的各向异性,不同磁化方向上的磁致伸缩特性也各不相同.但是所使用的磁特性测量装置为一维测量装置,只能产生单方向的激磁力.为了解决这一问题,测量总共准备7种样品,切割方向从轧向到垂直于轧向,间隔15°进行.测量时,与硅钢片磁特性测量标准一致,选择基波磁通密度幅值作为控制目标,设定值为0.5~1.6 T,步长为0.1 T.谐波磁场是在上述磁特性测量系统基础上开发实现的,可指定谐波次数和谐波占基波的百分比以及初相位.此外,该系统还可实现任意磁通密度波形的输入.
1.2.1 磁通密度和磁化方向对主应变的影响
图2给出了磁化角度为30°,10%的3次谐波注入时,不同基波磁通密度幅值下磁致伸缩主应变特性.主应变幅值随着基波磁密的增加而增加,而波形特征在样品饱和之前几乎没有变化.在同一磁化方向上主应变角度几乎不随磁密的增加而发生改变.图3比较了不同磁化方向的主应变特性,其中,3次谐波占基波幅值的10%,基波磁密幅值为1.0 .从图3中可以看出,磁化角度由0°增加到60°时,磁致伸缩主应变幅值随着磁化角度的增加而增加.其中,轧制方向与15°磁化方向主应变幅值较接近,30°和45°磁化方向磁致伸缩增加亦不明显,60°磁化方向主应变幅值最大.
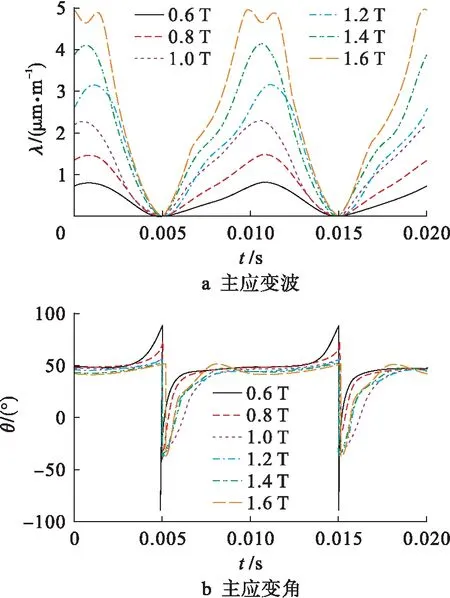
图2 3次谐波注入时的主应变特性Fig.2 Principal strain characteristics with injection of 3rd harmonics
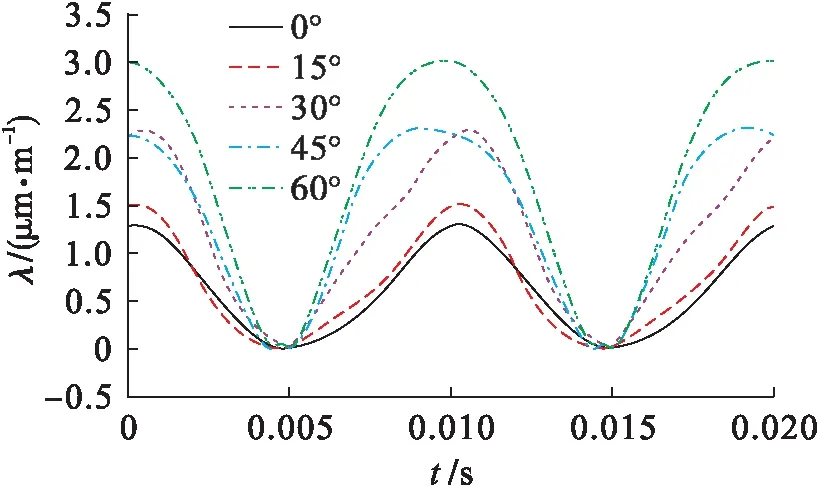
图3 3次谐波注入时不同磁化方向的主应变特性
1.2.2 谐波占比对主应变的影响
电工设备实际运行时,铁心中不同部位磁场的谐波含量亦不相同,本节分析不同谐波占比对磁致伸缩主应变特性的影响.
利用1.1节介绍的测量装置分别测量了谐波含量为8%和6%的3次谐波磁场作用下的磁致伸缩形变,并计算了主应变特性,如图4所示.从图4可以看出,在相同的基波磁密下,谐波含量越高,磁致伸缩应变峰值越大.随着谐波含量的减小,应变增加的趋势没有改变;随着磁通密度峰值的增加主应变峰值仍然增加;在接近饱和时,应变波形变得不再光滑,这说明此时主应变波形中的谐波含量更加丰富,呈现非线性特征.
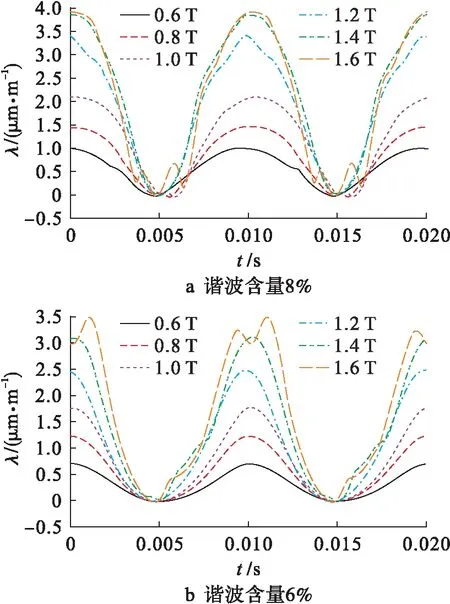
图4 45°磁化方向上的主应变特性Fig.4 Principal strain characteristics along 45° magnetization direction
1.2.3 谐波阶次对主应变特性的影响
根据测量数据,图5给出了在含有不同阶次高次谐波时,磁致伸缩主应变幅值λ随磁通密度幅值以及磁化方向变化的关系.从图5中可以看出,磁致伸缩应变的峰值λ不仅和磁化角度有关,还与磁通密度幅值密切相关,随着磁化角度和磁通密度增加而增加.而且,随着谐波阶次的增加和多次谐波同时存在时,硅钢片磁致伸缩主应变逐渐增大,在只含有3次谐波时,随着磁化角度和磁通密度峰值的增加,磁致伸缩主应变增加相对平滑.而在只含有5次谐波和3、5次谐波共存下,随着磁通密度和磁化角度增加,磁致伸缩主应变变化不再平滑,这是由于随着谐波次数的增加,磁致伸缩主应变中更高次谐波含量会增加,即非线性程度加深.

图5 磁致伸缩主应变幅值与磁化条件的关系Fig.5 Relationship between principal strain magnitude of magnetostriction and magnetization condition
2 动态矢量磁致伸缩模型和参数计算
文献[7]给出了旋转磁化下磁致伸缩主应变量和磁通密度矢量的关系,具体表达式为
(1)
式中:下标x、y分别为x、y方向的物理量;C为磁致伸缩主应变的直流分量;Kr和Ki分别为磁致伸缩主应变表达式的系数;τ=ωt为转角.
考虑到该模型可以描述磁致伸缩的动态时变特性,接下来将基于该模型建立非正弦磁化下磁致伸缩的动态矢量特性模型,并根据谐波磁场磁致伸缩特性,给出相应的主应变动态矢量模型的参数数据库建立方法.
2.1 动态矢量特性模型
非正弦磁化下,磁通密度波形可表示为
(2)
式中:n为第n个奇次谐波,例如,n=2表示第2个奇次谐波,即3次谐波,以此类推;N为最大奇次谐波个数;Bmax为磁通密度的基波幅值;θB为磁化角度;αn为注入的第n次谐波占基波幅值的百分比;φn为第n次谐波的初相位.若将式(2)做进一步处理,可表示为
I(2n-1)Bksin(2n-1)τ]
(3)
式中,k=x,y.将式(3)对τ求导,可以得到
(4)
将式(3)、(4)代入到式(1)中,则λk可以表示为
I(2n-1)Bkcos(2n-1)τ-(2n-1)R(2n-1)Bk·
sin(2n-1)τ]
(5)
考虑到磁致伸缩应变波形中包含直流分量和偶数次谐波,故其傅里叶展开形式为
(6)
式中:m为第m个偶次谐波;M为最大的偶次谐波个数;Ck0为磁致伸缩应变的直流分量;R(2m)λk、I(2m)λk分别为偶数次谐波的实部和虚部.为了确定最高保留谐波的次数,将测量的磁致伸缩应变波形进行傅里叶分解可以总结出,不论磁密在饱和区或非饱和区,大于8次的应变谐波分量均可以忽略不计,因此在后续建模过程中仅保留8次以内的谐波.基于上述分析,式(6)的磁致伸缩主应变表达式可简化为
(7)
比较表达式(5)、(7),发现式(7)中每一项都能在式(5)中找到对应项,于是,只需令对应项的系数相等,即可得到所提出模型的参数表达形式,即
Ck=Ck0
(8)

(9)
(10)
式中,参数Kkr和Kki为τ、θB以及Bm的函数,可以看到两模型参数值受到磁化方式的影响.
2.2 模型的参数计算及验证
作为验证,利用上述模型分别计算了3次谐波磁场注入时,磁化角度为75°,磁通密度幅值为1.58 T和磁化角度为45°,磁通密度幅值为1.12 T时的磁致伸缩主应变波形.实验测试结果对比情况如图6所示,可以看出模拟结果与实际测量数据基本吻合.

图6 测量与模拟磁致伸缩的波形比较Fig.6 Comparison between measured and simulated magnetostriction waveforms
3 结 论
本文利用实验室现有一维磁特性测量设备结合三轴应变花传感器及其附属设备测量了非正弦磁场磁化下硅钢片磁致伸缩特性,通过材料力学相关原理计算了磁致伸缩主应变波形及其主应变角,讨论了在基波磁场中注入不同阶次、不同占比高次谐波磁场时,磁致伸缩主应变的变化规律.结合实验数据分析给出了高次谐波磁场作用下磁致伸缩主应变动态矢量数学模型,推导了模型参数的计算表达式,建立了模型参数的数据库.最后,通过与实验数据的比较验证了模型的有效性.得到的结论如下:
1) 在非正弦磁场磁化下,主应变方向和磁化方向不一致,且两者的夹角随时间变化;
2) 注入同一频率高次谐波条件下,磁致伸缩主应变幅值随着谐波含量的增加而增加,当磁场接近饱和时,磁致伸缩主应变也相应趋于饱和;
3) 谐波含量相同时,随着高次谐波次数的增加,磁致伸缩应变峰值也增加,磁致伸缩回环不再光滑,磁致伸缩谐波含量增大,呈现非线性的特征;
4) 不同的磁化方向也会影响磁致伸缩主应变峰值的变化,随着磁化角度的增加,磁致伸缩主应变峰值与磁化角度呈现出线性增长的趋势,但同时又表现出各向异性的特点;
5) 磁致伸缩动态矢量数学模型可以有效地模拟高次谐波磁场作用下硅钢片的磁致伸缩特性,模型参数的表达式充分考虑了磁化方式的影响.
