地铁线路扣件刚度对钢轨振动与波磨的影响

朱宁 杨新文 赵治均

摘要：為探明整体道床轨道区段波磨发生机理及其对轮轨系统参数的影响规律，建立轮对和整体道床轨道三维有限元模型，分析轮轨共振模态与整体道床钢轨振动特性，探讨钢轨扣件刚度和轮对振动模态对整体道床区段钢轨波磨的影响规律。结果表明：钢轨扣件刚度主要影响钢轨起跳共振频率，而对钢轨pinned-pinned共振频率影响甚微;较低的扣件刚度将激发钢轨较大的振动，在特定频段上过大的钢轨振动会导致对应波长波磨的加剧，进而加速波磨的发展;钢轨在358 Hz下的横向弯曲变形是地铁整体道床区段线路产生特征波长为40 mm波磨的主要原因，故可采取减振措施抑制轮轨系统在358 Hz处的横向振动响应，从而抑制波磨的产生和发展。

关键词：地铁;整体道床;无砟轨道;扣件;车轮;振动;钢轨波磨;有限元

中图分类号：TP391.99;U213.53

文献标志码：B

文章编号：1006-0871（2021）03-0049-06

DOI：10.13340/j.cae.2021.03.009

Abstract：To explore the mechanism of rail corrugation in monolithic ballast bed track section and its influence on wheel rail system parameters， the three-dimensional finite element model of wheel set and monolithic ballast bed track is established. The wheel rail resonance mode and the vibration characteristics of monolithic ballast bed rail are analyzed， and then the effects of rail fastening stiffness and wheel set vibration mode on rail corrugation in monolithic ballast bed section are studied. The results show that the rail fastening stiffness mainly affects the rail take-off resonance frequency， but affects little on the pinned-pinned resonance frequency. The lower rail fastening stiffness stimulates the greater vibration of the rail， and the excessive rail vibration in a specific frequency band aggravates the rail corrugation of the corresponding wavelength， so as to accelerate the corrugation development. The transverse bending deformation of rail at 358 Hz is the main reason for the characteristic wavelength of 40 mm rail corrugation in the monolithic ballast bed section of metro. Therefore， vibration reduction measures can be taken to suppress the lateral vibration response of wheel rail system at 358 Hz， and then the generation and development of rail corrugation can be restrained.

Key words：metro;monolithic ballast bed;ballastless track;rail fastening;wheel;vibration;rail corrugation;finite element

0 引 言

钢轨波磨是长期困扰铁路建设的问题，尤其是在重载铁路建设中，这一问题更严重。我国城市轨道交通发展迅猛，尤其是轨道投入运行超过30年后，钢轨波磨问题越来越成为困扰城市轨道交通工务维修养护人员的一个重要问题[1]。钢轨波磨不会实质性地影响钢轨的使用和行车安全，但在波磨严重的地段，列车振动和噪声增大，轮轨受力增大，扣件系统和车辆转向架容易产生裂纹[2]，进而出现轨道部件破损（见图1），使轨道交通的运营成本增加，并影响轨道交通的运行安全。

各国学者对钢轨波磨的发生机理、特征和控制措施进行诸多研究，钢轨波磨的发生机理是认识并控制波磨的前提。目前，学者们最为认可的波磨机理是固定波长机理和损伤机理。GRASSIE[3]将波磨按照不同的固定波长机理和损伤机理分为响轨波磨、车辙型波磨、P2力共振波磨、重载波磨、轻轨波磨和轨道形式波磨等6类。谷永磊[4]研究分析高速铁路无砟轨道钢轨波磨的成因与分类。金学松等[5]按照波磨是与系统固有特性相关还是由初始不平顺发展而来，将其成因总结为自激振动理论、反馈振动理论和其他理论等3类。钢轨波磨发生机理复杂，影响因素众多，与车辆-轨道结构系统中各个部分均有一定关联，因此至今未有一种统一的机理解释各种波磨现象。在对实际线路中发生波磨的机理进行研究时，需要综合车辆、线路、轨道、轮轨关系等各方面，研究梳理出誘发钢轨引起波磨的关键影响因素。

为控制地铁线路环境振动，各种类型的减振轨道涌现。研究表明，在各种类型的减振轨道上，钢轨波磨发生的概率仍均较大[6-7]。钢轨高弹性扣件是一种有效的轨道减振结构，可以较好地控制列车引起的环境振动，但减振扣件轨道区段的钢轨波磨问题愈发凸显，如先锋扣件、浮轨等[8]。已有研究大多数集中在现场观测的定性诠释上[9]，对于整体道床减振扣件地段钢轨波磨的理论仿真、轨道结构参数与轮轨关系的匹配方面研究较少。钟硕乔等[10]将实测钢轨短波波磨不平顺数据作为不平顺激励，通过数值计算，得到在科隆蛋扣件线路上不平顺发展过程中车辆动力学响应的变化情况。

为探明整体道床轨道区段波磨发生机理及其对轮轨系统参数的影响规律，以苏州城市轨道交通为研究对象，建立轮对和整体道床轨道三维有限元模型，分析轮轨共振模态与整体道床轨道钢轨导纳特性，研究该区段钢轨波磨的产生原因，探讨钢轨扣件刚度与轮对振动模态对整体道床轨道区段钢轨波磨的影响规律。

1 轨道和轮对有限元模型

1.1 整体道床轨道有限元模型

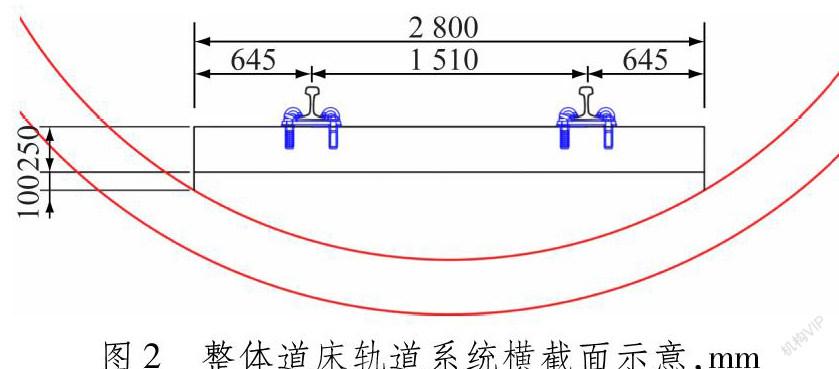
为系统研究分析苏州城市轨道交通整体道床区段的钢轨振动特性，采用有限元软件Abaqus建立整体道床轨道结构三维实体有限元模型。轨道结构有限元模型的参数参考苏州城市轨道交通实际建设线路的设计参数，其横截面参数见图2，有限元模型的动力学参数见表1。

针对所建立的轨道系统三维实体有限元模型，使用Lanczos法进行轨道系统模态分析，提取轨道系统的固有频率及其对应模态，分析轨道系统容易产生激烈动力响应的激励频率及其对应的振动形态。在钢轨和轨下结构模型中，为降低内部动力波的端部反射对轨道结构振动特性的影响，钢轨纵向长度应足够长。参考国内外有关的计算模型[11]，确定轨道系统的模型长度为25 m，可以反映列车运行过程中近似无限长钢轨的振动特性。轨道系统结构在横截面上均为对称结构，为提高计算速度，建立单股轨道结构的对称模型。最终建立的整体道床轨道三维有限元模型见图3。

1.2 轮对有限元模型

车辆轮对同样参考苏州城市轨道交通运营广泛使用的B型电客车的有关设计数据，其中车轮的主要参数为轴重14 t、轮径840 mm，轴型为RC3。建立的车辆轮对三维有限元模型见图4。

2 整体道床轨道导纳特性与波磨关系

2.1 轮对与整体道床轨道模态分析

2.1.1 整体道床轨道模态分析

整体道床无砟轨道在0～2 000 Hz范围内共有2 332阶模态，其前50阶固有频率见表2，轨道的典型振型见图5。由此可知，整体道床无砟轨道的轨下基础几乎不参与振动，前12阶振型为钢轨的横向弯曲变形，从第13阶开始以钢轨的垂向弯曲变形为主，其中第16阶振型伴有钢轨的横向弯曲。

2.1.2 轮对模态分析

对城市轨道交通B型车的轮对进行自由模态分析，即不加任何外部约束，使其具有与动力学模型相同的自由度。与轨道系统模态分析方法相同，最终得到轮对在0～2 000 Hz范围内的固有频率及其对应的振型。轮对的固有频率及其典型振动分布分别见图6和7。

轮对的振动形式有径向振动、轴向振动、径向弯曲和轴向弯曲等。

2.2 整体道床轨道导纳特性分析

为全面反映钢轨的振动特性，计算0～10 000 Hz频率范围内的垂向和横向钢轨位移导纳，计算步长为1 Hz。对于整体式道床轨道系统，钢轨垂向位移导纳见图8。钢轨在不同频率下均会产生振动，其中有2种典型的振动形式，对应各个导纳峰值：钢轨共振和pinned-pinned共振。钢轨共振频率即导纳图中的第一个峰值对应频率180 Hz。钢轨pinned-pinned振动是指支撑于两根轨枕之间的钢轨受到激励后产生的纵向机械波，其驻波节点刚好在轨枕处。第一个峰值之后的各个峰值均属于pinned-pinned振动，其频率主要有1 100、3 160、5 138和7 800 Hz。

整体式道床轨道系统的钢轨横向位移导纳见图9。其振动特性与重型钢弹簧轨道结构的钢轨类似，有2种典型的振动形式：横向钢轨共振和横向pinned-pinned共振，并且在190～508 Hz频率范围内持续震荡，存在一系列导纳峰值，此频段的振动与线路的短波长波磨关系密切。

综合分析图8和9可知，在列车运行过程中，整体式道床轨道系统的钢轨振动响应峰值频率主要有104、180、190、212、238、263、294、326、360、405、434、471、508、684、842和1 100 Hz等，在这些频率下，钢轨的动力响应更加剧烈，可能由此产生更加严重的钢轨磨耗。结合轨道系统和轮对模态分析结果，在列车运行过程中容易发生剧烈的轮轨共振而造成严重磨耗的频率主要有263、358、405和471 Hz，对应频率下的轮轨振动模态见图10。

进一步结合苏州城市轨道交通的波磨现场实测数据，在线路区段处，其现场工程情况条件与所建立的整体道床轨道三维实体有限元模型相同，经过现场测试数据处理和分析[12]，得到其波磨特征波长为40和200 mm。此区段列车的实际运营车速为50 km/h，短波波磨的特征波长40 mm对应频率约为347 Hz。考虑到实际运营过程中的车轮轮对的附加质量，相同振动形态下轮轨系统的动力响应频率应略低于轨道系统本身在外界单独激励下的振动频率，因此该线路的短波波磨对应的钢轨振动频率应约为358 Hz。由图10b可知，此频率下钢轨和轮对的振动形态以横向振动为主，也就是说，钢轨在358 Hz下的横向弯曲变形是此区段线路产生特征波长为40 mm波磨的主要原因。通过采取减振措施，重点抑制轮轨系统在358 Hz处的横向振动响应，降低钢轨在此频率的振幅，可以降低对应波长的周期性钢轨磨耗，进而抑制波磨的产生和发展。

2.3 扣件刚度的影响分析

2.3.1 扣件垂向刚度

在保持其他参数不变的情况下，分别将扣件垂向刚度取值5、10、20、30、40和50 kN/mm，计算分析钢轨跨中简谐力激励下激励点处钢轨的垂向导纳，结果见图11。

改变轨道系统的扣件垂向刚度，主要影响钢轨在0～1 000 Hz频率范围内的垂向振动特性。具体来说，钢轨在10和200 Hz附近的导纳峰值明显改变，但不会影响钢轨的pinned-pinned振动。当扣件垂向刚度过小（小于5 kN/mm）时，该峰值频率接近20 Hz从而表现不明显，整个频段内钢轨的振幅都很大。在特定频段上，过大的钢轨振动会导致对应波长的磨耗加剧，从而加速波磨的发展。在与波磨特征波长相关的364 Hz附近，存在一系列导纳峰值，适当增大扣件刚度可以明显降低振幅，有助于抑制波磨的发展。

2.3.2 扣件横向刚度

在保持其他参数不变的情况下，分别取钢轨扣件横向刚度值为2、5、10、15和20 kN/mm等5种情况，计算分析钢轨跨中简谐力激励下激励点处钢轨的横向导纳，见图12。

改变钢轨扣件横向刚度，主要影响钢轨0～800 Hz频率范围内的横向振动特性。具体来说，钢轨在100 Hz附近、160～500 Hz中多个频率和700 Hz附近的导纳峰值明显改变，但不影响800 Hz附近的振动峰值，说明增大扣件横向刚度会导致该峰值频率提高，对应的导纳峰值同时略微减小。在与波磨特征波长相关的频率364 Hz附近，存在一系列导纳峰值，适当增大扣件横向刚度可以明显降低振幅，有助于抑制波磨的发展。

3 結 论

建立轮对和整体道床轨道三维有限元模型，进行模态分析和导纳分析，研究线路扣件刚度对钢轨导纳特性与波磨的影响，得到以下结论。

（1） 钢轨扣件刚度主要影响钢轨起跳共振频率，对钢轨pinned-pinned共振频率影响甚微。

（2） 钢轨扣件刚度降低，将激发钢轨较大的振动，在特定频段上过大的钢轨振动会导致对应波长波磨的加剧，进而加速波磨的发展。在与波磨特征波长相关的400 Hz附近，存在一系列导纳峰值，适当增大扣件刚度可以明显降低振幅，有助于抑制波磨的发展。

（3） 钢轨在358 Hz下的横向弯曲变形是此区段线路产生特征波长为40 mm波磨的主要原因，可通过采取减振措施，重点抑制轮轨系统在358 Hz处的横向振动响应，降低钢轨在此频率的振幅，降低对应波长的周期性钢轨磨耗，进而抑制波磨的产生和发展。

参考文献：

[1] ZHAO X， WEN Z F， WANG H Y， et al. Modeling of high-speed wheel-rail rolling contact on a corrugated rail and corrugation development[J]. Journal of Zhejiang University：Science A， 2014， 15（12）：946-963.

[2] 李伟. 地铁钢轨波磨成因及其对车辆/轨道行为的影响[D]. 成都：西南交通大学， 2015.

[3] GRASSIE S L. Rail corrugation：Characteristics， causes， and treatments[J]. Proceedings of Institution of Mechanical Engineers， Part F：Journal of rail and rapid transit， 2009， 223（6）：581-596. DOI：10.1243/09544097JRRT264.

[4] 谷永磊. 高速铁路无砟轨道钢轨波浪形磨损机理研究[D]. 北京：北京交通大学， 2017.

[5] 金学松， 李霞， 李伟， 等. 铁路钢轨波浪形磨损研究进展[J]. 西南交通大学学报， 2016， 51（2）：264-273. DOI：10.3969/j.issn.0258-2724.2016.02.006.

[6] 关庆华， 张斌， 熊嘉阳， 等. 地铁钢轨波磨的基本特征、形成机理和治理措施综述[J]. 交通运输工程学报， 2021， 21（1）：316-337. DOI：10.19818/j.cnki.1671-1637.2021.01.015.

[7] 李响. 地铁减振轨道结构振动及钢轨波磨研究[D]. 北京：北京交通大学， 2019.

[8] CUI X L， CHEN G X， YANG H G， et al. Study on rail corrugation of a metro tangential track with Cologne-egg type fasteners[J]. Vehicle System Dynamics， 2016， 54（3）：353-369. DOI：10.1080/00423114.2015.1137955.

[9] 張厚贵. 北京地铁钢轨波磨的机理及整治方案研究[D]. 北京：北京交通大学， 2015.

[10] 钟硕乔， 吴磊， 李伟， 等. 钢轨波磨对地铁车辆动力学响应的影响[J]. 计算机辅助工程， 2012， 21（6）：26-30. DOI：10.3969/j.issn.1006-0871.2012.06.006.

[12] 杨新文， 翟婉明. 轨道交通轮轨噪声机理、预测与控制[M]. 上海：同济大学出版社， 2017：40-46.

（编辑 武晓英）