隧道洞口上方危岩崩塌块石运动规律及其对隧道的危害
2021-11-28周广强王方昭祝介旺
周广强 王方昭 祝介旺


摘要:為揭示危岩崩塌块石的运动规律及其对下方隧道洞口的危害,以都香高速昭通段乐红隧道洞口高陡边坡危岩区崩塌体为研究对象,运用理论计算与Rockfall数值计算2种形式对危岩区崩塌体失稳后块石的运动特征进行预测,运用Abaqus有限元软件模拟不同初速度、不同冲击落点下块石冲击隧道结构的动力响应,揭示不同因素对块石冲击隧道结构的影响程度。结果显示:理论计算与Rockfall数值计算结果吻合,崩塌块石经坠落、碰撞、滚动最终会与隧道引洞段上表面发生碰撞;与冲击落点相比,块石初速度对隧道结构的动力响应特性影响更大;块石冲击落点位于隧道圆拱圆心正上方位置时对隧道结构的损伤最大;不同冲击落点对碰撞回弹后块石的速度影响不大。
关键词:崩塌;块石;冲击;位移;速度;运动特征;动力响应
中图分类号:TP391.99;TU457
文献标志码:B
文章编号:1006-0871(2021)03-0031-07
DOI:10.13340/j.cae.2021.03.006
Abstract:To study the movement law of dangerous rock collapse block and its damage to the tunnel portal below, taking the collapse block in the dangerous rock area of the high and steep slope above the entrance of Lehong tunnel in Zhaotong section of Duxiang expressway as the research object, two forms of theoretical calculation and Rockfall numerical calculation are used to predict the movement characteristics of rock collapse blocks after mass instability in dangerous rock area. The dynamic response of rock block impacting on tunnel structure with different initial velocities and impact points are simulated by Abaqus finite element software, and then the influence of different factors on the performance of rock block impacting on tunnel structure is revealed. The theoretical calculation results is consistent with the Rockfall numerical calculation results, and the collapse block will eventually collide with the upper surface of the tunnel approach section after falling, collision and rolling. Compared with the impact point, the initial volocity of rock block has a greater influence on the dynamic response characteristics of tunnel structure. While the impact point of collapse block is located directly above the center of the tunnel arch, the damage to the tunnel structure is the largest. The velocity of collapse block after impact rebound changes little with the different impact points.
Key words:collapse;block;impact;displacement;velocity;movement characteristics;dynamic response
0 引 言
危岩崩塌灾害是山区常见的重要地质灾害之一,其随机性大、发生频率高、分布面广,难以准确预测,对山区公路、隧道、建筑、人员等经济和生命财产造成很大威胁。由于崩塌灾害的复杂性和不确定性,崩塌的研究成果也比较分散。
国内对危岩崩塌运动的研究虽然起步较晚,但在理论方面也取得一定的成果。张路青等[1-2]研究川藏公路滚石的发生频率,并通过分析遭遇滚石的概率、承灾体的易损性,得到经过不同滚石区时车辆和行人遇灾的风险,同时提出困难条件下滚石发生频率的估计方法;陈洪凯等[3]依据危岩整治的经验,将危岩失稳崩塌模式划分为坠落式、倾倒式和滑塌式3种类型;何思明等[4]根据接触理论,在材料的弹塑性特性的基础上,提出滚石法向碰撞恢复因数和切向碰撞恢复因数的具体计算公式;黄润秋等[5]选取不同形状和质量的石块在同一坡面上进行落石试验,得出石块的形状、质量及坡面状况对落石运动特征的影响;唐红梅[6]运用Rockfall软件模拟崩塌落石的运动特征,并与现场试验结果对比,两者较为接近;张晓科等[7]利用刚体极限平衡法和FLAC3D对危岩体在4种不同工况条件下的稳定性进行评价和预测,并提出危岩防治措施;袁博等[8]运用LS-DYNA动力有限元软件,模拟在滚石冲击最不利工况下棚洞结构改进前、后的动力响应;杨璐等[9]运用Abaqus有限元软件模拟不同速度和冲击角度下滚石冲击载荷对棚洞结构的动力响应。现有的危岩崩塌运动研究成果大多为理论研究,鲜有与实际工程相结合,而且研究的受影响工程结构形式大多为棚洞或桥梁结构,少有隧道结构。
本文以都香高速昭通段乐红隧道洞口高陡边坡危岩区崩塌体为研究对象,采用理论计算与数值模拟对比的方法对其崩塌后的运动特征进行计算对比,揭示该危岩区崩塌块石的运动规律,运用Abaqus有限元模拟的方式,对崩塌块石冲击接引隧道的动力响应进行模拟,通过设置不同工况,揭示不同因素对块石冲击隧道结构的影响程度。
1 工程概况
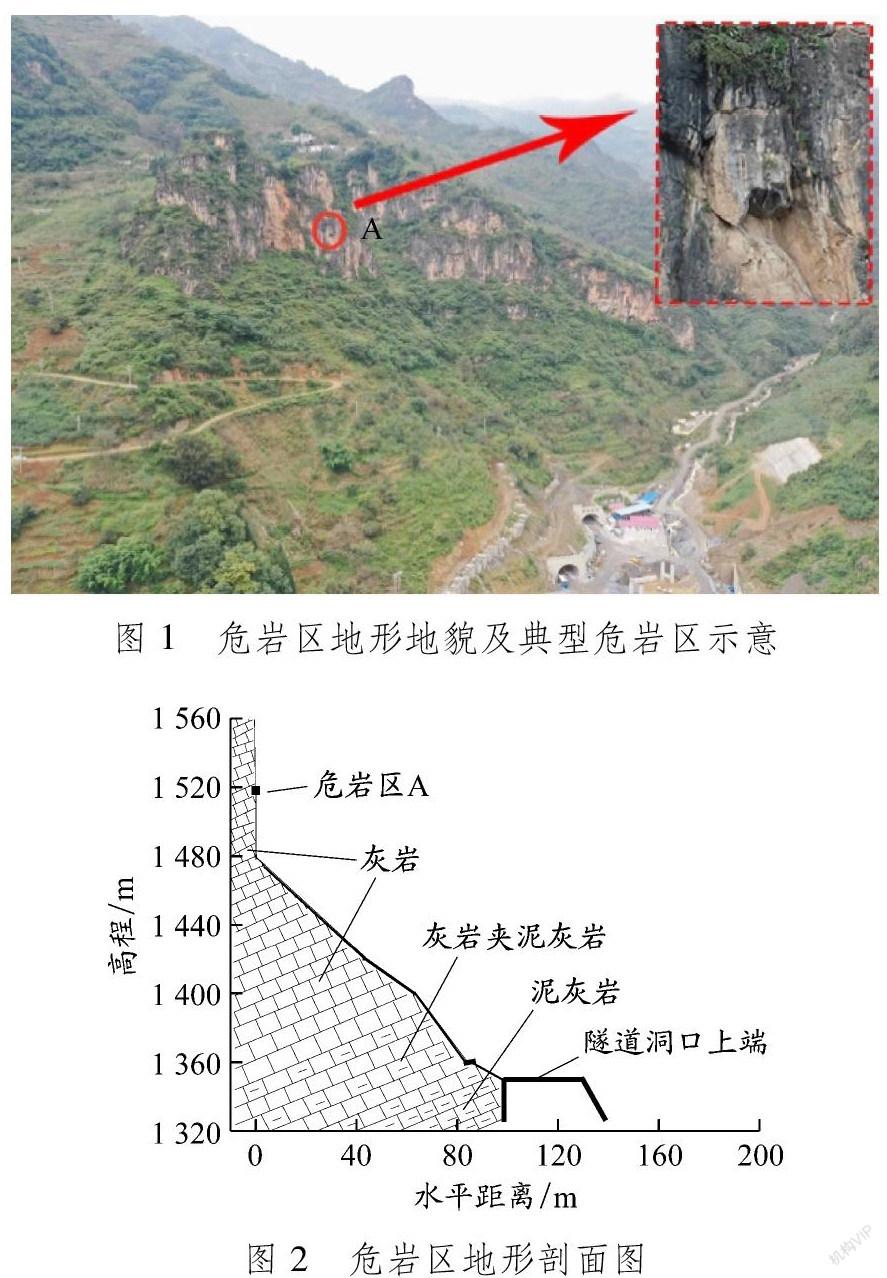
乐红隧道位于云南省昭通市鲁甸县乐红乡,是都香高速的控制性工程,隧道全长9 757 m,本文研究对象是都香高速乐红方向的隧道进口高陡边坡危岩区崩塌体。研究区属高山峡谷地貌,地势总体东高西低。隧道进口位于西侧山体坡底,危岩区主要分布于西侧山体上部,山顶高程1 565 m,隧道进口上端高程1 350 m,高差215 m。危岩所处山体总体地形为“上陡下缓”,上部为基岩出露的陡崖,下部为坡度较缓的斜坡。上部陡崖出露基岩岩性为灰岩,植被茂盛。斜坡表面整体覆盖碎石土、块石土等堆积物,植被茂盛,底部岩性由上而下依次为灰岩、灰岩夹泥灰岩和泥灰岩。经现场资料收集与调查,确定10余处危岩区,主要分布高程为1 410~1 564 m,相对隧道进口处高差为70~224 m,属高位、特高位危岩。本文选取典型危岩区A崩塌体作为研究对象,危岩区A地形地貌及典型危岩区位置见图1,危岩区A地形剖面见图2。
危岩区A分布高程为1 510~1 517 m,相对隧道进口处高差为160~167 m,属于特高位危岩区。危岩区平面面积为10 m2,整体体积为66 m3,属中型规模危岩区。出露岩性为灰岩,岩体节理裂隙发育,裂隙填充物较少,主要为岩屑和泥土。岩体结构为块状结构。危岩区发育有3组节理,该危岩体受层面切割,底部临空,且受重力卸荷作用影响。自然边坡临空面的倾角大于65°,且岩体被结构面切割后已经形成不稳定块体,结构面赤平投影图见图3。结构面的交点M2、M3与自然边坡临空面在同侧,即控崩结构面组合交线的倾向与坡面临空面倾向一致,但倾角小于坡角,易发生坠落式崩塌[10]。
2 危岩区崩塌块石运动过程分析
为分析危岩区崩塌块石对隧道工程造成的冲击响应,对崩塌块石的运动过程进行预测,得到块石运动路径和运动特征。通过理论计算与数值模拟对比,揭示崩塌块石运动规律。
2.1 理论计算
根据唐红梅等[11]和吕庆等[12]对危岩区崩塌块石运动路径理论分析的研究,对危岩区A的崩塌块石运动路径和运动特征进行理论计算。各坡段坡面角度及恢复因数[13]取值见图4,其中Rn为法向恢复因数,Rt为切向恢复因数。
2.1.1 初始运动阶段
危岩区A属坠落式危岩,失稳后垂直落下,只受自身重力作用。加速度取9.81 m/s2,初始速度为0,则块石坠落轨迹方程为
式中:u为块石的速度,m/s;g为重力加速度,m/s2;t为时间,s;H为坠落高度,m。
2.1.2 碰撞阶段
运动的崩塌块石与斜坡发生碰撞,块体的速度方向与碰撞接触点的法线方向不一致,因此需要将块石的速度分解为坡面的法线和切线方向,
式中:uf为块石速度的法向分量,m/s;uq为块石速度的切向分量,m/s;u1x为块体初始水平方向速度,m/s;u1y为块体初始竖直方向速度,m/s;α为坡面角度,(°)。
崩塌块石与坡面碰撞后的速度损失,由法向恢复因数Rn和切向恢复因数Rt确定。恢复因数能够反映块石的碰撞行为,不同坡面垫层的恢复因数取值不同。本文根据唐红梅等[13]总结的恢复因数取值表取值,具体见图4。
塊石与坡面碰撞后,将崩塌块石的速度分解到水平方向和竖直方向上,
式中:u2x为块体碰撞后水平方向速度,m/s;u2y为块体碰撞后竖直方向速度,m/s。
此时,若崩塌块石在坡面法线方向上的速度分量不为0,则块石做斜抛运动。假设块石在水平方向上不受空气阻力,竖直方向上只受自身重力作用,则块石运动路径为抛物线。
2.1.3 滚动阶段
当崩塌块石与坡面碰撞后,块石在坡面法线方向上的速度分量为0,块石不会进行斜抛运动,而是将沿着坡面发生滚动。当块石发生滚动时,根据动力学理论可得块石的加速度
式中:a为块体加速度,m/s2;k为阻力特性因数。
2.2 数值计算
采用Rockfall数值模拟软件,对危岩区崩塌块石的运动路径和运动特征进行分析。影响块石运动的因素众多且复杂多变,因此Rockfall软件有以下假定:(1)将斜坡坡面简化成折线,忽略坡面细微因素的影响;(2)将块石简化为刚性球体,忽略碰撞、滚动过程中的表面损伤;(3)忽略块石的形状影响;(4)忽略空气阻力对块石的影响。
块石运动数值模拟步骤为:(1)在Rockfall软件中按实际情况建立坡体形状;(2)根据坡面的情况,选取切向恢复因数、法向恢复因数、动摩擦因数,设置材料属性(各因数和材料属性的选取与理论计算相同);(3)将材料属性赋予每一个坡面;(4)设置危岩区崩塌块石位置,设置随机崩塌块石数为20个;(5)进行模型计算和分析。
2.3 结果对比
2.3.1 运动轨迹
危岩区崩塌块石的理论运动轨迹与模拟运动轨迹对比见图5。
(1)崩塌块石从起崩点自由落体到A点,在A点与坡体发生碰撞,弹跳至BC段内再次发生碰撞,继而沿BC段坡面滚动到C点。此阶段内的理论计算路径与模拟计算路径基本一致。
(2)块石在C点与坡体发生碰撞,弹跳一段距离后沿坡面滚动至D点。此阶段内的理论计算路径与模拟计算路徑略有不同,理论计算所得块石弹跳距离略大。
(3)块石在DE段内发生碰撞后,运动至E点。此阶段,理论计算路径所得块石发生2次碰撞后到达E点,而模拟运动轨迹显示块石为1次碰撞后到达E点。
(4)块石在E点与坡面发生碰撞后,弹跳至隧道进口上端。此阶段内理论计算路径与模拟计算路径相似,但模拟计算所得块石弹跳高度及弹跳距离略大。
总体上来看,理论运动轨迹与模拟运动轨迹基本吻合,个别阶段内运动轨迹略有不同。崩塌块石第一次与隧道进口上端接触时,2种计算路径位置有所不同。理论计算结果显示块石第一次与隧道进口上端接触位置为从左侧起2 m处,模拟计算结果显示块石第一次与隧道进口上端接触位置为从左侧起2~8 m处。
2.3.2 平移速度
选取A~G以及隧道洞口上端从左侧起2、5、8 m共10个点,对比理论计算与模拟计算得到的崩塌块石平移速度。后3个点取块石与隧道洞口上端第一次接触时的平移速度,模拟计算结果取平均值,结果见表1。
(1)A~G点理论计算与模拟计算结果基本一致,模拟计算结果略偏大。
(2)隧道洞口上端从左侧起2 m处,理论计算轨迹显示崩塌块石与隧道洞口上端第一次接触时块石的平移速度为18.01 m/s,而模拟计算轨迹显示15%块石与隧道洞口上端第一次接触,接触时块石的平移速度平均值为16.77 m/s。
(3)隧道洞口上端从左侧起5 m处,理论计算结果可忽略不计,模拟计算轨迹显示20%块石与隧道洞口上端第一次接触,接触时块石的平移速度平均值为18.24 m/s。
(4)隧道洞口上端从左侧起8 m处,理论计算可忽略不计,模拟计算轨迹显示5%块石与隧道洞口上端第一次接触,接触时块石的平移速度平均值为20.03 m/s。
3 冲击响应数值模拟
为研究崩塌块石对隧道洞口上端的冲击响应,采用Abaqus有限元软件进行模拟。为得到块石冲击对隧道的最不利影响,模型参数、载荷参数等均按最不利条件取值。
3.1 有限元模型
纵向长度前15.0 m的隧道洞口裸露在外,上端没有回填土、堆积物等垫层覆盖,因此有限元模型取15.0 m长度。隧道立面尺寸为上端31.0 m,下端39.5 m,高度22.0 m,圆拱高度14.5 m、宽度22.0 m。由于崩塌块石的形状尺寸较为复杂又各不相同,难以完全按实际情况建模,为简化模型,根据现场观察测量坡面堆积块体的尺寸,将块石模型设置为半径1 m的刚性球体R1。隧道采用C3D8R单元划分网格,局部加密;崩塌块体采用C3D4单元类型进行动态三维应力分析。为更好分析崩塌块体对隧道结构的影响,在隧道圆拱P点处建立参考点,见图6。
3.1.1 材料参数与本构关系
崩塌块石采用刚体模型,忽略运动和撞击过程中的变形,块石密度为2 500 kg/m3,弹性模量为5 000 MPa,泊松比为0.45。隧道材料混凝土等级为C30,钢筋为HRB335,为简化模型,采用混凝土塑性损伤模型对隧道进行等效计算,混凝土密度取2 500 kg/m3,泊松比取0.20,弹性模量取34 500 MPa。
3.1.2 其他设置
(1)相互作用与约束。崩塌块石与隧道结构的相互作用采用表面与表面接触。将崩塌块石设置为刚体约束,在块石圆心设置参考点,在分析开始时将参考点调整至质心。
(2)边界条件与预定义场。将隧道底面的所有节点施加全约束,允许位移与转角值均为0。将崩塌块石设置于隧道上表面0.1 m高度处,在预定义场中给予块石初速度。
(3)工况设置。根据块石冲击点位置,设置隧道上端从左侧起2、8、14、20和26 m等5种工况,块石初速度设置20和30 m/s等2种工况,初速度方向为y方向。
3.2 结果分析
3.2.1 不同冲击落点影响
当块石初速度为20 m/s时,在不同块石落点工况下,隧道表面接触点的位移曲线见图7。在块石冲击阶段,隧道表面接触点的位移急剧增大;在块石回弹阶段,接触点经历弹性恢复后进入塑性状态,位移值趋于平衡。冲击落点从隧道上端左侧向右侧逐渐移动,最终平衡时接触点的位移值逐渐增大,但增幅较小。最终平衡时接触点的位移最大值为0.015 m,此时的冲击落点是20 m处。分析其原因,受隧道整体结构的影响,隧道圆拱的圆心正上方位置即为20 m处,此处结构抗冲击性能略显薄弱。总体而言,接触点位移受不同冲击落点的影响不大。
当块石初速度为20 m/s时,在不同冲击落点工况下,P点位移曲线见图8。P点位移曲线成波浪状,且随时间变化循环往复,但幅度逐渐减小。从波动幅度来看,位移最大值依次为落点2、8、26、14和20 m工况,其中落点为14 m工况与20 m工况的幅度大小差别不大。位移最大值是冲击落点为20 m工况时的0.000 41 m。
当块石初速度20 m/s时,不同冲击落点工况下块石x方向速度曲线见图9。块石在0.005 s时与隧道上表面接触,0.010 s到达最低点,然后发生回弹,回弹过程中与弹坑边缘有轻微摩擦,最后脱离弹坑。块石冲击落点自隧道上端左侧向右侧移动时,块石x方向速度隨之增大。其原因是回弹速度受块石与隧道碰撞后回弹恢复因数的影响。总体而言,块石与隧道表面发生碰撞后,x方向速度增幅不大,最大值是落点为26 m处时的0.20 m/s,最小值是落点为2 m处时的0.11 m/s;在不同落点工况下块石x方向速度差距不大,最大差值仅为0.09 m/s。
在不同落点工况下,块石以20 m/s初速度冲击隧道上表面时,块石y方向速度曲线见图10。块石与隧道上表面碰撞后,y方向速度急剧减小至0,之后发生回弹,速度方向发生改变,在与弹坑边缘有轻微摩擦后脱离弹坑。由于未设置重力作用,脱离弹坑后,落石y方向速度趋于平衡。在冲击落点为2 m工况下,块石y方向速度趋于平衡时为13.46 m/s;在冲击落点为8 m工况下,块石y方向速度趋于平衡时为13.60 m/s;在冲击落点为14 m工况下,块石y方向速度趋于平衡时为13.34 m/s;在冲击落点为20 m工况下,块石y方向速度趋于平衡时为13.21 m/s;在冲击落点为26 m工况下,块石y方向速度趋于平衡时为13.00 m/s。总体而言,块石y方向速度受落点位置影响不大。
3.2.2 不同初速度影响
在块石冲击落点2 m工况下,取不同块石初速度,隧道表面接触点的位移曲线见图11。在块石冲击阶段,隧道表面接触点位移急剧增大,在块石回弹阶段,隧道表面接触点经历弹性恢复后进入塑性状态,位移值趋于平衡。块石初速度为20 m/s时,接触点位移由0快速增大到0.047 m,后恢复至0.013 m趋于平衡。块石初速度为30 m/s时,接触点位移由0快速增大到0.055 m,后恢复至0.018 m趋于平衡。与冲击落点位置相比,隧道表面接触点位移受初速度的影响较大:初速度越大,碰撞后的接触点位移越大。
在块石冲击落点为2 m工况下,取不同块石初速度,P点位移曲线见图12。P点位移曲线成波浪形状,随时间变化不断变化,从波动幅度来看,初速度20 m/s时的最大位移小于初速度30 m/s时的位移。初速度为20 m/s时的最大位移值为0.000 11 m,初速度为30 m/s时的最大位移值为0.000 29 m,可知P点位移受初速度的影响较大。
在块石落点为2 m工况下,取不同块石初速度,块石回弹x方向速度曲线见图13。当块石初速度为20 m/s时,块石回弹x方向速度先由0快速增至0.10 m/s,后缓慢增至0.11 m/s趋于平衡。块石初速度为30 m/s时,块石回弹x方向速度先由0快速增至0.36 m/s,后缓慢增至0.37 m/s趋于平衡。块石回弹x方向速度受初速度影响较大,块石初速度越大,碰撞回弹后块石的x方向速度越大。
在块石冲击落点为2 m工况下,取不同块石初速度,块石回弹y方向速度曲线见图14。块石初速度20 m/s时,块石y方向速度在块石与隧道表面碰撞后骤减至0,之后块石回弹,y方向速度增至4.50 m/s,最终块石脱离弹坑时y方向速度为13.46 m/s。块石初速度30 m/s时,块石y方向速度在块石与隧道表面碰撞后骤减至0,之后块石回弹,y方向速度增至17.51 m/s,最终块石脱离弹坑时y方向速度为19.42 m/s。与冲击落点位置相比,块石y方向速度受初速度的影响较大,初速度越大,碰撞回弹后的块石y方向速度越大。
4 结 论
以都香高速昭通段乐红隧道洞口高陡边坡危岩区A崩塌体为研究对象,采用理论计算和数值模拟对比的方法对其崩塌后的运动特征进行预测分析,揭示该边坡崩塌体的运动规律;采用Abaqus有限元软件模拟崩塌块石冲击隧道的动力响应,揭示不同因素对块石冲击隧道的影响程度,结论如下。
(1)理论计算与Rockfall数值模拟结果对比显示,两者得到的危岩失稳崩塌后的运动特征基本吻合,崩塌块石最终会与隧道上表面发生碰撞,对隧道结构造成不利影响。
(2)有限元数值模拟分析结果表明,块石初速度对冲击的动力响应影响较大:块石初速度越大,碰撞回弹后的速度越大,隧道结构的损伤越严重。块石冲击落点对隧道结构的动力响应也有一定的影响:与其他落点相比,当落点位于隧道圆拱圆心正上方位置时隧道结构的损伤略大。不同落点对碰撞回弹后块石的速度影响不大。
针对危岩区崩塌失稳风险,后续有必要对其进行主动加固處理,或在崩塌运动的路径上设置防护网、格构梁等被动防护结构,避免崩塌块石对隧道结构造成不利影响。针对隧道结构上表面,建议铺设碎石土层、橡胶垫层等缓冲垫层,且隧道圆拱上方的表面应重点防护。
参考文献:
[1] 张路青, 杨志法. 公路沿线遭遇滚石的风险分析:案例研究[J]. 岩石力学与工程学报, 2004, 23(21):3700-3708.
[2] 张路青, 杨志法, 张英俊. 公路沿线遭遇滚石的风险分析:方法研究[J]. 岩石力学与工程学报, 2005, 24(S2):5543-5548.
[3] 陈洪凯, 欧阳仲春, 廖世荣. 三峡库区危岩综合治理技术及应用[J]. 地下空间, 2002, 22(2):97-101. DOI:10.3969/j.issn.1673-0836.2002.02.001.
[4] 何思明, 吴永, 李新坡. 滚石冲击碰撞恢复系数研究[J]. 岩土力学, 2009, 30(3):623-627.
[5] 黄润秋, 刘卫华, 周江平, 等. 滚石运动特征试验研究[J]. 岩土工程学报, 2007, 29(9):1296-1302. DOI:10.3321/j.issn:1000-4548.2007.09.003.
[6] 唐红梅. 群发性崩塌灾害形成机制与减灾技术[D]. 重庆:重庆大学, 2011.
[7] 张晓科, 秦四清, 李志刚, 等. 西龙池抽水蓄能电站下水库BW2危岩稳定性分析[J]. 工程地质学报, 2007, 15(2):174-178. DOI:10.3969/j.issn.1004-9665.2007.02.006.
[8] 袁博, 祝介旺. 滚石冲击下棚洞破坏动力响应分析及改进对策:以川藏公路(安久拉山南麓)门式棚洞为例[J]. 水文地质工程地质, 2019, 46(6):57-66. DOI:10.16030/j.cnki.issn.1000-3665.2019.06.08.
[9] 杨璐, 李士民, 吴智敏, 等. 滚石对棚洞结构的冲击动力分析[J]. 交通运输工程学报, 2012, 12(1):25-30. DOI:10.19818/j.cnki.1671-1637.2012.01.005.
[10] 王孝健, 苏生瑞, 成良霞. 汶川地震区映秀—卧龙公路边坡崩塌类型的赤平投影解法[J]. 中国地质灾害与防治学报, 2012, 23(1):48-54.
[11] 唐红梅, 易朋莹. 危岩落石运动路径研究[J]. 重庆建筑大学学报, 2003, 25(1):17-23. DOI:10.3969/j.issn.1674-4764.2003.01.004.
[12] 吕庆, 孙红月, 翟三扣, 等. 边坡滚石运动的计算模型[J]. 自然灾害学报, 2003, 12(2):79-84. DOI:10.3969/j.issn.1004-4574.2003.02.014.
[13] 唐红梅, 李阳, 王林峰. 三峡库区陡高边坡落石运动特性数值模拟分析[J]. 重庆师范大学学报(自然科学版), 2019, 36(4):49-54. DOI:10.11721/cqnuj20190411.
(编辑 武晓英)