基于优化VMD的滚动轴承故障诊断方法

毛坤鹏 贝绍轶

摘    要：当滚动轴承出现不同严重程度的故障时，所提取的特征用于诊断中识别率较低。为解决这一问题，根据变分模态分解的原理，提出使用改进的蝙蝠算法优化变分模态分解的参数，利用优化后的参数对故障信号进行分解，以求得样本的能量熵和能谱熵。根据三个筛选因子对分量进行筛选，求取保留分量的主频分布特征。将能量熵、主频分布特征、能谱熵作为特征向量输入到支持向量机中进行故障识别。实验表明，提取的特征提高了故障状态的识别率。

关键词：变分模态分解;参数优化;改进的蝙蝠算法;故障诊断

中图分类号：TP277               文献标识码：A                 文章编号：2095-7394（2021）04-0076-09

由于滚动轴承的故障信号是非线性非平稳信号，且通过传统的频谱分析难以准确提取故障特征频率，HUANG等人[1]提出了经验模态分解法（EMD）。区别于传统的信号处理方法，EMD无需设置基函数，其通过自适应方法可将信号分解为若干IMF分量和一个残余分量，每个分量均包含信号在不同时间段的局部特征;但EMD方法也存在端点效应以及模态混叠的问题。为此，WU等人[2]将白噪声加入到原信号中，并通过多次添加，平均多次分解的结果，完成了噪声的抵消，使模態混叠现象得到了明显的消除。随后，DRAGOMIRETSKIY等人[3]于2014年提出了变分模态分解方法，该方法有可靠的数学理论基础，其通过引入变分框架求解约束变分模型最优解，从而将原信号分解为一系列调幅调频信号;然而，该方法虽能有效避免模态混叠及端点效应，但模态数K和二次惩罚因子alpha的选取会对最后的分解效果产生影响。

本文使用改进的蝙蝠算法，以最小平均包络熵为适应度函数对VMD分解的参数进行寻优，并使用优化后的参数对信号样本分解，从而求取优化参数组合[K，α]下的能量熵以及能谱熵;同时，使用三个筛选准则对分量进行筛选，求取筛选后分量的主频分布特征，将能量熵、主频分布特征、能谱熵作为特征向量输入到支持向量机中进行训练，进而实现不同故障状态的识别。

1    基本理论

1.1  变分模态分解理论

变分模态分解就是将信号分解转为在变分框架内求解变分问题。信号经过变分模态分解得到[K]个IMF分量，每个IMF分量都有不同中心频率的带宽，中心频率和带宽会随着迭代的进行产生变化。变分模态分解的目标就是求能使所有分量的估计带宽之和最小，且各分量之和等于原始信号时所对应的[K]个分量。由此，变分模态分解这一算法流程其实质就是变分问题的构造与求解。所构造的变分模型表达式为：

[ui][ωi][λ]的迭代方程分别为式（3）、式（4）、式（5）。采用乘法算子交替方法项（ADMM）的方法对增广拉格朗日表达式中的[ui][ωi]交替更新，分量和中心频率更新后再对乘法算子[λ]更新，直到满足终止条件（6）。

1.2  蝙蝠算法

2010年，YANG[4]受蝙蝠利用超声波回声定位觅食行为的启发，提出了蝙蝠算法。该算法中蝙蝠的位置代表了所求解，在每次迭代过程中，蝙蝠个体的脉冲频率和强度都实现更新，从而改变个体的位置。通过求取每个位置所对应的适应度值，达到最大迭代次数后可得到最优解。具体步骤如下。

（1）初始化蝙蝠个体的位置[xi]、速度[vi]、响度[A]、脉冲率[r]、响度衰减系数[Af]、脉冲频度增强系数[Rf]、种群数量[N]以及最大迭代次数[Tmax]。

（2）根据适应度值确定当前种群中的最优位置[x?]，通过式（7）、式（8）、式（9）更新蝙蝠个体的位置和速度：

其中：[fi]表示每个蝙蝠个体的声波频率;[β]表示1个[0，1]之间的随机向量。

（3）以式（10）、式（11）来模拟蝙蝠发现猎物后减小响度、增大脉冲频率的捕食特性：

（4）达到最大迭代次数后，输出蝙蝠最佳位置;否则，返回步骤（2）。

2    变分模态分解参数的优化

2.1  VMD参数优化步骤

模态数[K]和惩罚因子[α]的选取会对信号的分解结果造成很大影响。模态数过大，信号会过分解;过小，则会欠分解。惩罚因子过大，会造成信息缺失;过小，会导致低频分量包含过多冗余分量。

对于[K]和[α]值的确定，前人大都通过先确定[K]值，再寻找最优适应度值所对应的[α]来确定最佳的[K]和[α]的组合。然而，根据刘建昌等人[5]的研究，这种先定[K]再定[α]的方法只能得到一个相对最优的参数组合，并不一定是全局最优的参数组合;因此，考虑使用蝙蝠算法来寻找最佳参数组合。

轴承的故障信号经过VMD分解后，会得到若干个模态函数。与正常信号相比，故障信号中的冲击成分更多，各分量的能量较为集中，包络熵[6]较小。使用蝙蝠算法优化VMD参数时，选用最小平均包络熵[7]作为目标函数。平均包络熵的定义式为：

其中：[N]表示信号采样点数;[K]表示信号总分解个数。

由于蝙蝠算法存在易陷入局部最优、早熟后种群的多样性会降低等问题;因此，使用改进的蝙蝠算法对参数组合进行寻优，具体步骤如下。

（1）初始化蝙蝠算法的基本参数。

（2）采用混沌映射的方法生成蝙蝠个体的初始位置。随机生成一个2维的[0，1]上的向量[Zi=（Zi1，Zi2）]，根据式（13）迭代生成[N-1]个向量：

此时，蝙蝠个体的初始位置便可通过式（14）生成：

（3）计算所有个体初始位置的适应度值，将最优适应度值所对应的个体位置确定为当前最优位置。在速度更新公式中添加一个权重因子[ω]，权重因子的表达式如下：

式中：[pfitness（i）]表示个体的适应值;[best min]表示当前全局最小适应度值;[best max]表示当前全局最大适应度值。此时，速度更新公式便由式（8）变为式（16）。

（4）按照式（9）完成所有蝙蝠个体的位置更新，然后，用标准蝙蝠算法进行局部寻优以及更新响度和脉冲频率。

（5）重复步骤（3）（4），达到最大迭代次数后，输出最小平均包络熵所对应的蝙蝠个体位置。此时，该个体位置即为VMD的最佳参数组合。

2.2  仿真验证

通过式（17）构造一组故障仿真信号，分别以标准蝙蝠算法和改进的蝙蝠算法对VMD的参数进行寻优。

式中：[η]表示均值为0标准差为0.1的高斯白噪声;仿真信号的采样频率为2 000 Hz，采样点数为500。

利用改进的蝙蝠算法和标准蝙蝠算法进行参数寻优，两种算法的寻优过程如图1。改进的蝙蝠算法和标准蝙蝠算法分别在第5、第9次迭代后寻找到全局最小平均包络熵，此时，所对应的参数组合为[4，800]。仿真信号以参数组合[4，800]进行变分模态分解后，得到了4个分量，前3个分量分别对应着组成仿真信号的3个谐波信号，VMD分解后的4个分量信号其时域波形图和频谱图如图2。

从图2可以看到，仿真信号以参数组合[4，800]完成VMD分解后，3个谐波信号的频率都得到了体现。

3    分量筛选

信号经过变分模态分解后，分量可能存在与原信号无关、含有噪声以及不能反映原信号冲击特征等问题。

基于以上问题，选用峭度值、边际谱熵的倒数、相关系数作为筛选准则，共同对分解出的分量进行选择，从而选出最能凸显原信号特征的分量。信号中的噪声越少，则边际谱熵[8]的倒数越大。边际谱熵的定义如下：

式中：[h（i）]表示信号经过变分模态分解后第[m]个分量的边际谱。

由于这3个筛选准则对分量的影响权重会随着原信号选取的不同发生改变;因此，考虑将这3个筛选准则的值分别表现为三维直角坐标系中3个轴上的数值，即每个分量都有3个分别在坐标系3个轴上的点。为了统一3个筛选准则的数量级，将这些点的坐标设为（峭度值，0，0）（0，10*边际谱熵的倒数，0）（0，0，10*相关系数）。将这3个点相连后，可得到一个三角形，然后，选取三角形面积最大的分量。由3个筛选准则的数值构成的三角形如图3。

4    特征向量構造

特征向量既要能对不同故障有较好的区分性，又要能对不同工况、不同损坏程度的相同故障具有较好的聚集性。为了完成对不同故障的识别，本文选取能量熵、能谱熵和主频分布特征作为特征向量。

4.1  能量熵

信号经过变分模态分解后，每个IMF分量都有自己频段的信息[9]，当滚动轴承发生故障时，一些频段的分量会发生变换，进而导致瞬时能量的变化;同时，不同故障的能量熵值也会发生变化。能量熵的计算方法如下：

4.2  能谱熵

当轴承出现不同程度的故障时，信号在各个分量中的分布会发生改变，而随着故障程度的加深，能量分布的改变，能谱熵[10]的大小随之变化。能谱熵的计算公式如下：

式中：[pi]的定义和式（19）中相同;[m]表示VMD分解的总分量个数。

4.3   主频分布特征

当滚动轴承发生故障时，周期性的冲击会改变轴承的振动信号频率结构，信号经过傅里叶变换转化为频域信号后，可以通过频域特征中的主频分布特征[11]来表征谱能量分散程度，从而对不同的故障加以区分。主频分布特征的计算公式如下：

式中：[K]表示频谱线数;[fk]表示第[k]条频谱线的频率值;[s（k）]代表频谱。

5    故障状态识别过程

滚动轴承的状态大体可分为正常、内圈故障、滚动体故障和外圈故障4类，而轴承出现的故障又可按退化程度分为轻度、中度和重度;因此，滚动轴承状态总共可以分为10种，对每种状态都定义一个标签，每种状态的信号选取80组。

利用改进的蝙蝠算法确定变分模态分解的参数组合，以该参数组合对每组信号进行变分模态分解，并根据分解出的分量信号以及分量个数计算能量熵和能谱熵。使用筛选准则抉择出最优分量后，计算最优分量的主频分布特征，将这3个特征作为每组信号的特征向量。选取每种故障状态的前60个样本作为训练样本，训练结束后，再将每种故障状态的后20组作为测试样本输入到SVM中，对10种故障状态进行分类。整体的故障状态识别流程如图4。

6    实例分析

本文的实验数据来源于美国西储大学电气工程实验室。轴承参数如表1所示，驱动端的轴承型号为6205-2RS JEM SKF，该轴承为深沟球轴承，滚动体个数为9。

本文的实验数据选取负载为0 W、转速为1 797 rpm、采样频率为12 000 Hz的数据。内圈故障、滚动体故障、外圈故障（6点钟方向）分别选取0.177 8 mm、0.355 6 mm，0.533 4 mm三种损伤直径;然后，再选取负载为0、转速为1 797 rpm的正常数据，构造10种故障状态。每种故障状态选取80组数据，每组数据的采样点数为1 024个。

如表2所示，为10种故障状态所对应的标签以及各故障状态经过改进的蝙蝠算法寻优后所得的最优参数组合。

随机选取一组内圈轻度故障信号，使用最优参数组合[6，3 744]作为变分模态分解的参数[K]和[α]，各分量的包络谱图如图5。

从图5中可见：内圈轻度故障信号按照最优参数组合分解后，每个分量都包含了电机的2倍转频58.59 Hz和内圈故障特征频率164.1 Hz。

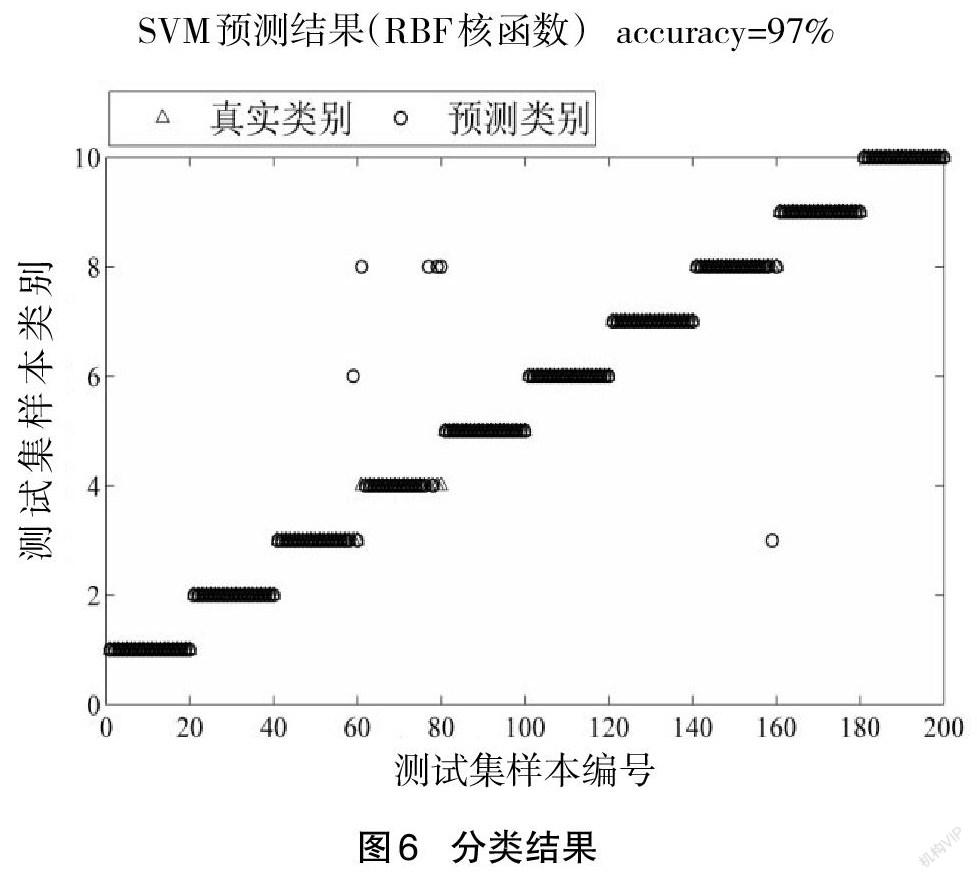
使用最优参数组合对10种故障状态的信号进行变分模态分解，求取能量熵、能谱熵、主频分布特征组成的特征向量，每种故障状态都能获取80组特征向量;选取其中60组作为训练样本，20组作为测试样本。10种故障状态下200组测试样本的分类结果如图6。

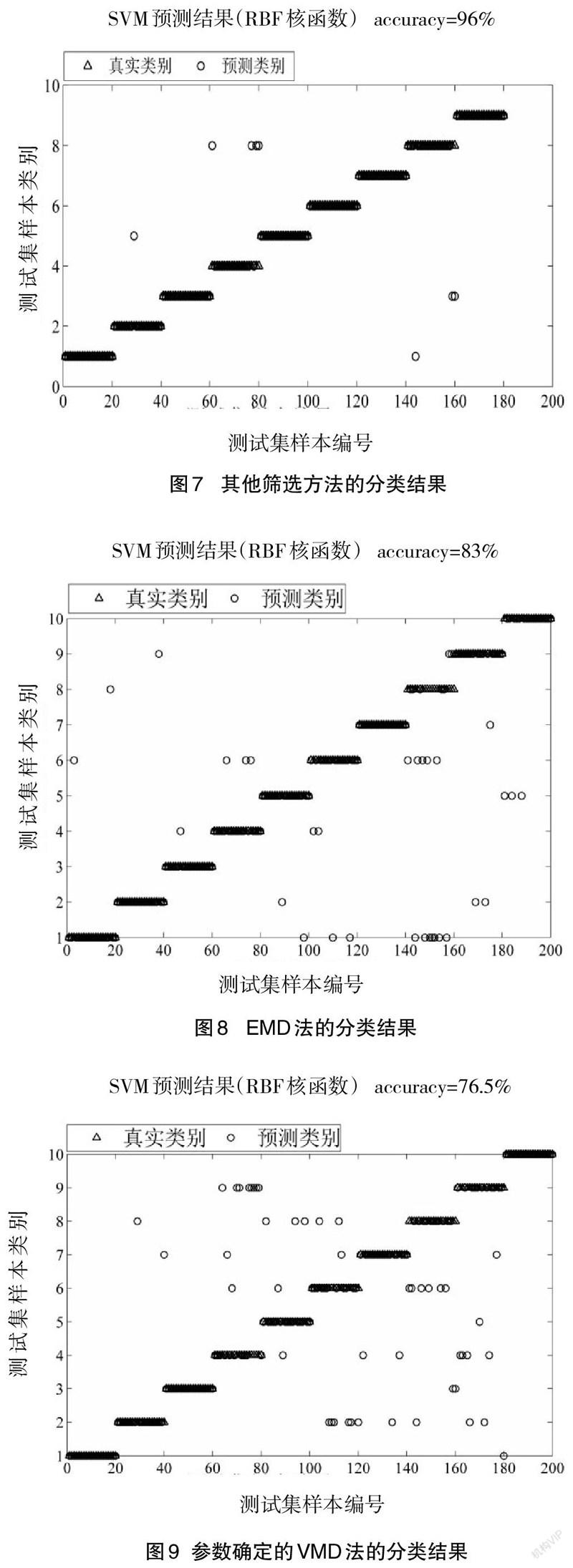
从图6可见：200个测试样本有6个出现了预测错误，主要是将4个标签4的样本错分类为标签8。为了体现本文筛选方法的有效性，将原故障状态识别过程中的筛选过程改为先提取相关系数较大的2个分量，再比较2个分量的峭度值，最终保留峭度值较大的分量。根据此法所产生的预测类别与真实类别的对比如图7。

从图7可见：使用其他筛选方法后，标签4有4个错误预测，标签8出现了3个错误预测，即有2个故障状态出现了较多的错误识别;而本文的方法只在1个标签类别处出现了较集中的错误预测，且整体的预测正确率更高。

为了验证本文参数优化方法的有效性，分别使用EMD法、参数组合确定为[5，2 000]的VMD法分解相同的故障信号，故障状态的识别流程与前述相同。这2种方法的预测结果如图8、图9。

从图8和图9可以看到：与EMD法和参数确定的VMD法相比，本文的方法对10种故障状态都有较高的识别率，且不存在对多个标签类别有错误预测的情况。

7   结语

以提高轴承故障状态的识别率为目的，本文提出了一种优化的滚动轴承故障诊断方法：（1）将平均包络熵作为优化目标，利用改进的蝙蝠算法对VMD参数进行寻优;（2）以峭度值、边际谱熵的倒数、相关系数作为筛选准则，对分解出的分量进行选择;（3）将能量熵、能谱熵、主频分布特征作为滚动轴承的故障特征。实验结果表明，该方法提高了对轴承不同故障状态的识别率。

参考文献：

[1] HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1998，454（1971）： 903-995.

[2] WU Z，HUANG N E. Ensemble empirical mode decomposition： a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis，2011，1（1）：1-41.

[3] DRAGOMIRETSKIY K，ZOSSO D.Variational mode decomposition[J]. IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[4] YANG X S. A new metaheuristic bat-inspired algorithm[J]. Science，2010，284：65-74.

[5] 刘建昌，权贺，于霞，等.基于参数优化VMD和样本熵的滚动轴承故障诊断[J].自动化学报，2019-08-12（网络首发）.DOI10.16383/j.aas.190345.

[6] 丁承君，付晓阳，冯玉伯，等.基于参数优化VMD的齿轮箱故障特征提取方法[J].机械传动，2020，44（3）：171-176.

[7] 谷然，陈捷，洪荣晶，等.基于改进自适应变分模态分解的滚动轴承微弱故障诊断[J].振动与冲击，2020，39（8）：1-7.

[8] 徐波.基于机器学习的旋转机械故障诊断方法的研究[D].武汉：武汉科技大學，2019：83-84.

[9] 张超，朱腾飞，王大勇.基于VMD能量熵与支持向量机的齿轮故障诊断[J].机械设计与研究，2018，34（2）：81-84.

[10] 段永彬，张玉芝，安建良，等.基于变分模态分解谱熵的电机轴承退化状态识别方法[J].机械设计与研究，2019，35（4）：101-104.

[11] LEI Y G，HE Z J，ZI Y Y， et al. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs[J]. Mechanical Systems and Signal Processing，2007，21（5）：2280-2294.

责任编辑    盛    艳