自制量角器探知角的度量单位和量角原理

刘静娴

[摘 要]用量角器量角是度量教学的一个难点，不仅因为测量从一维线段扩充到二维平面，而且它有别于面积度量，只能依靠实体工具来直接测量，无法通过相关基础参数来计算，因此借助前面的度量单位概念来类比推理和确立角度单位，十分必要。

[关键词]自制量角器;角度单位;量角;原理

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0067-02

笔者有幸聆听了一节北师大版教材四年级“角的度量”一课，该课发人深省，许多地方值得称道。执教者能够始终围绕“学生的发展”展开教学，教学效果出奇的好，十分难得，这需要高超的授课技巧。对于这难得一见的好课，笔者觉得有必要记录下来，以期与同行切磋探讨。

一、体会量角的必要性

首先，教师围绕“角的大小指的是什么？”这个问题，请学生展开讨论，并描述什么是角的大小，进而让学生理解什么是角的大小。再以问题“人类研制出量角器前，是如何度量角的大小的？”触发学生思考。

然后，教师话锋一转，提示道：“这个问题有点突然，我们先来回顾一下以前的测量方法，看是否能带来一些灵感。”学生在脑海里搜索：测量长度是用1厘米、1分米这样的线段来度量，测量面积则是用1平方厘米、1平方分米这样的小正方形来度量，从而归纳出一个通行规则：大角可以用规定好的小角来度量。

【设计意图：通过类比推理，唤醒学生过去测量物体的经验，归纳出度量单位的制定规则与使用过程，推理出角度的测量也需要制定固定大小的角度作为角的专用度量单位，用单位角的个数去度量大角的度数。这样不但激发了学生的探究欲，而且降低了难度，给学生铺好了台阶，引导学生构建了度量知识的庞大体系，发展了学生的创造力。】

二、体会统一单位的必要性

接着，分组测量、拼摆，测量某大角（给定的大角）里包含几个单位角。有的学生测量的结果是3个小角，为3度，有的学生测量的结果是4个小角，为4度，而有的学生测量的结果是5个小角，为5度，结果各异。这时学生发现不对劲，同一个角不可能存在几个度数，于是学生觉察到有必要统一度量单位，也就是“要用同一个小角作为单位角”“要制定一个约定俗成的单位标准”。

【设计意图：这个环节独具匠心，制造了认知冲突，不但让学生通过相互矛盾的实验结果觉察到单位角度出了问题，而且还产生统一单位大小的需求。学生在活动交流中进一步体会到度量单位的制定需慎重，同时更加清醒地认识到度量单位测量的运作原理，即小角不断累加形成大角，小角的个数就是大角的度数。此时，学生的学习兴趣空前高涨，教师再详细介绍1度角及1度角的来历与写法则水到渠成。】

三、发明量角器，理解量角原理

定好了统一标准的角度单位（1度），接着进行初次测量：以1度角为单位角，估测5度、10度角的大小;以10度角为单位角，估测20度、60度角的大小。在检验估测结果的时候，课件展示1度角、10度角不断叠加铺满大角的过程，让学生在计数的过程中感受角度和长度一样可以连续密铺叠加。

【设计意图：估测是教学的一大难点，因为小学生从未体验过几何特性上的叠加，即通过几何形状上的叠加来推算理解数量上的叠加，而教师让学生用1度作为单位角来估测5度角，转而又将5度作为单位角来估测10度角，再转而将10度作为单位角去估测20度、60度角，层层递进，不断更换度量单位，有序扩大度量单位，使单位角这个表象更加完整和立体，同时学生的度量意识也有所加强。】

教师提问：“用1度的角作单位可以度量任何大小的角，那是不是就代表每个角都得一五一十地一度一度地去连接覆盖？（出示一个60度角）这个角也需要用1度角去一个个度量吗？（学生自然而然地想到了用量角器）如果不用量角器，我们自力更生，自创一个单位角去度量，可以吗？”（明明有量角器，为何要舍近求远、舍易求难，自创单位角呢？到底搞什么名堂？作为旁观者，笔者心里不禁犯嘀咕：为什么不顺应“民心”，从量角器开始研究，非要设置障碍呢？）

学生集体商议后得出的法子是“用1度角拼出一个合适的大小”，创造一个新单位角，再来测量就方便得多，这样数数的次数会变少。拼成的新单位可以是直角、周角。

课件演示用1度角组接成一个半圆形简易量角器，所有1度角的顶点集中在一个定点上，此点就是量角器的中心点;接着讨论该怎么使用，如何摆放，如何读数。有的学生一板一眼地数出1度角的个数，有的半途而废，嫌烦琐。于是教师引导学生改良量角器，标上刻度，这样就不用一个个去数了。学生进一步改进工艺：1度一个间隔标出刻线太密集，难以辨认，10度一个间隔标出刻线较为合理。学生尝试用自制量角器量角。

由教师量出图1中角1、角2的度数，学生通过观察反思，指出并纠正教师操作的不当之处，总结出量角的一般方法。学生在测量角3的度数时，出现40度和140度两种结果。学生发现角度的开口方向与量角器的读数方向相反，无法正确读数，需进一步改进量角器：在外层再反向标明一圈刻度，形成内外两圈刻度，同一位置两圈刻度数的示数和为180度。这样制成的量角器就比较合格了。

【设计意图：设计这一环节的初衷是为了完善量角器。然而在加工改进的过程中，却有意外的收获：学生不仅知道了角的一边与量角器0刻线的哪半段重合，读数时的起始刻度就是哪半段，另一条边指向的刻度数就是被测角的大小，量角原理就是从量角器上找出一个和待测角大小相同的角。】

四、使用量角器，掌握測量方法

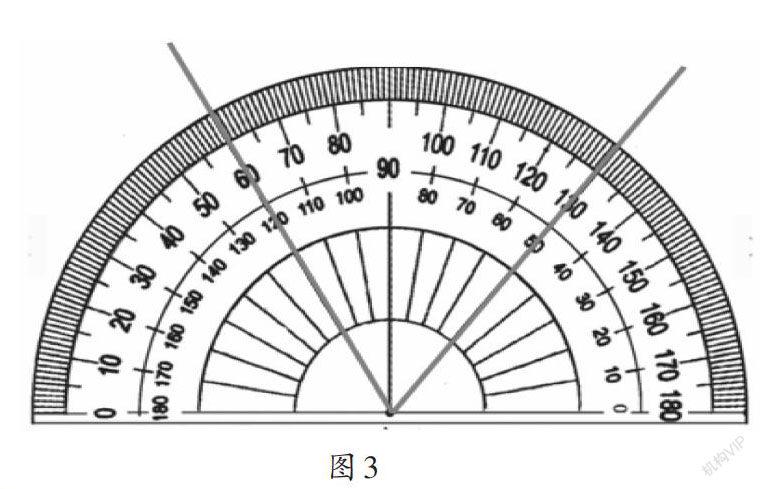
教师先出示钝角和锐角，让学生判断应该顺着哪一圈刻度读数，然后出示只画了一条边的角，这条边正好指向50度刻度线（如图2），让学生猜测它的度数。学生猜测可能是50度或130度。课件出示70度角（如图3），由学生解释70度是怎么得到的。

【设计意图：引导学生观察对比自制量角器与正规量角器，进一步认识量角器，并在正规量角器上定角、画角、量角，巩固和总结测量方法。】

五、教学思考

本节课给笔者留下的深刻印象主要有三方面：

一是教学设计能做到为学生量体裁衣。课前，教师对学生进行调查采访，发现了很多问题。如学生对角的大小的感知很模糊，对量角器的结构和工作原理一知半解，对测量要领和测量方法也知之甚少。为此，设计了自制量角器环节，让学生边制作边思考测量原理，从而深刻理解角的大小概念。

二是能按学生的思路循循善诱。从学生熟悉的长度、面积的度量单位入手，迁移类比到角的单位的制定与测量，推导出大角可以用小角来量，但是小角要统一标准，顺利引出角的度量单位——1度角。有了1度角作单位，可以估测5度角的大小，再将5度角定为大一级的单位估测10度角的大小，然后将10度角作为更大一级的单位，估测20度、60度角的大小。按这个思路，任何角都可以估测，但是如何精确测量呢？角的度量工具应运而生。

学生将1度角不断叠加，制成一个简易量角器。该如何标记刻度呢？经过研究，统一认为10度作为一个间隔较为科学。接着就要付诸实践，投入使用。当测量图1中的角3时，学生发现不对劲。就这样，学生在不断化解认知冲突的过程中，改进和完善了量角器，同时对量角原理也有了一个透彻深刻的认识，思维更缜密，思路更清晰。

三是能根据学生思维的发展方向来设计数学活动。在实际教学中，因为量角器的普及度很高，有的教师干脆让学生拿来就用，在使用中再慢慢理解量角原理，掌握量角、画角方法，形成操作技能。这是不符合思维发展规律的，学生可能会怀疑量角器的必要性，因而产生制造量角器这一现实需求才是思维的起点。

本节课依靠丰富的有启发意义的活动，充分调动学生的学习积极性，让学生经历知识的生成和演变的过程，真正实现以学定教，按需供给，这样的课堂才是鲜活的。

（责编 罗 艳）